深层神经网络预训练的改进初始化方法❋

周佳俊❋❋，欧智坚

（清华大学电子工程系，北京100084）

深层神经网络预训练的改进初始化方法❋

周佳俊❋❋，欧智坚

（清华大学电子工程系，北京100084）

在基于神经网络的语音识别任务中，提出根据激励函数二阶导数优化网络预训练阶段中权值初始化的方法。利用激励函数的非线性区域和自变量呈高斯分布的特性，寻找权值分布的较优方差以提升训练速度。通过比较同一学习速率下不同初始化数值对收敛速度的影响，发现此种方法可以加快预训练阶段的速度，提升神经网络训练的效率。

语音识别；深层神经网络；预训练；初始化；激励函数

1 引言

近年来，利用深层神经网络进行语音识别中的声学模型建模成为了热点问题，其准确率已经超越了传统的混合高斯模型加隐含马尔科夫模型（Gaussian Mixture Model-Hidden Markov Model，GMM-HMM）的建模方式［1］。层数的增加能够提升网络的识别能力，使之容纳更多的信息，但同时也使BP算法（Back Propagation Algorithm）更容易陷入局部极小值中，这是利用神经网络进行模型训练以来一直存在的问题。

预训练（Pre-training）的引入在一定程度上缓解了该问题带来的影响，以无监督方式最大化训练数据的似然值，可以使训练的参数对象值更接近BP算法寻找的全局最优区域［2］，其实际的效果也令人满意。在进行BP算法之前加入预训练的过程，能够将系统识别率进一步提升［3］。

预训练给BP算法提供了一种参数初始化的方式，但在预训练开始之前，神经网络中权值矩阵和阈值的初始化仍然依靠经验和尝试。本文通过分析神经网络中激励函数的特性，提出参数的初始化应该参考该函数非线性区间的方法。在相同的学习速率下，实验验证该改进初始化方法能够有效提高预训练的收敛速度。

2 神经网络声学模型

2.1模型结构

利用神经网络实现的声学模型结构如图1所示，输入层的每个节点对应从训练数据中提取出的语音特征的每一维，经过若干隐层的传递后，在输出层得到与音素个数相同的类别输出。其中权值矩阵W0和W1以及每一层的阈值，是本文要进行初始化研究的对象。通常情况下，网络每个节点的激励函数采用逻辑斯谛（logistic）函数，即

在模型训练的过程中，输入层提供每一个语音帧的特征向量，同时在输出层提供该帧对应的类别标注向量，利用BP算法从后向前传递误差值，对参数进行逐层的更新。文献［4］描述了经典的BP算法流程，这里不再赘述。

图1 利用神经网络实现的声学模型示意图Fig.1 Schematic diagram of acoustic model based on DNN

2.2 预训练

随着数据量的增加，所使用的神经网络层数也不断上升，从起初的只包含输入输出层发展到目前在语音识别领域最常使用的附加4～6个隐层。网络规模的扩大使识别能力随之提高，但参数的不断增多也使BP算法容易陷入局部极值的缺点显得愈发突出。

为了解决这一问题，文献［1］提出了将神经网络的每相邻两层及其权值矩阵看作一个受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）的观点。设输入层的数据为向量I，输出层的数据为向量O。如果此RBM位于神经网络的最底层，也即I是语音特征向量，则其被称作高斯受限玻尔兹曼机（Gaussian RBM，GRBM）。

对于一个普通的RBM，其输入和输出向量I和O均为二进制向量，每个分量只能随机地取0或1。通过定义能量函数和联合概率分布，可以计算得出这两个向量对彼此的条件分布为

式中，W为权值矩阵，f为逻辑斯谛函数，α和β分别为输入层和输出层的阈值向量。由于I和O各自的内部分量都是相互独立的，因而根据式（2）可以求出已知向量I的情况下O中每个分量等于1的概率，由式（3）可知反之亦然。

在预训练的过程中，根据式（2），可以先将已有的输入向量进行一次前向传递，即得到已知I时O的后验概率，接下来利用此概率对其进行一次采样，得到二进制的采样结果O；之后利用式（3），将O作为输入数据反向传递，得到已知O时I的后验概率并采样，得到结果向量I；再将I作为输入数据重复第一步的前向传递过程，得到采样结果O。以上过程被称作对I和O的一次重建。

利用原有数据和重建结果，就可以对此RBM的权值和阈值进行梯度下降法的更新。设最大化的目标函数为L，则权值、阈值的更新公式如下：

式中，E表示求期望，L实际为训练数据在此网络下的似然值。

最后，使用数据的重建误差描述训练的正确性与进度，该误差定义为

其中，Ii表示第i个输入节点的值，N为输入节点的个数。式（7）的值也就是输入数据和其本身重建数据之间的误差平方和。随着训练的进行，该误差会逐渐下降直至稳定在一个较小的范围内。误差值随数据量的下降曲线则反映了训练的速度，在之后的实验部分，就是利用了这一曲线的形状来比较收敛的快慢。

乌村是独立于乌镇东西栅的高端乡村旅游度假区，是乌镇旅游股份有限公司的又一新品牌。古镇旅游开发基本上靠门票经济，除此之外就是购物与餐饮，经营的业态比较单一。而乌村围绕江南农村村落特点，内设酒店、餐饮、娱乐等一系列的配套服务设施，主打“一假全包”，所以在乌村吃住方面就不存在二次消费。为了创造额外收入，就需要从其他方面入手，童玩馆精品店就是其他收入的重要来源。

3 参数初始化方法

预训练使得BP算法省去了参数初始化的步骤，与此前根据经验确定初始值的方式相比，有了更多的理论支撑，效果也更好。但在初始化预训练参数时，目前的研究仍处在依靠经验或者尝试的阶段［5］。

本文认为，神经网络之所以能在表现上超过GMM-HMM模型，主要原因在于它能综合利用数据间的线性和非线性关系，其中前者依靠权值矩阵及阈值实现，后者则通过非线性的激励函数来实现。非线性关系的引入，决定神经网络能够将数据间的关系刻画的更深刻，文献［6］中也提到了相同的观点。

因而，通过初始化参数，让神经网络的激励函数更好地工作在非线性区间，就可能加速网络对数据的适应过程，从而提高训练的收敛速度。式（1）表示的逻辑斯谛函数是神经网络中最常用的激励函数，也是本文引用的所有文献都采用的传递方式。这里有一个非常重要的前提条件，目前语音识别领域使用神经网络对声学模型进行构建时，输入的数据会在每一维上归一化到标准正态分布。因此输入层的每个节点都是一个服从N（0，1）分布的数据，即式（7）中的Ii服从该分布。

由于阈值的作用与权值矩阵有所重叠，按照一般的做法，初始时的阈值可以设为0，因而RBM的输出层第j个节点的总输入值为

接下来，Netj将成为逻辑斯谛函数的自变量。而根据上述假设，I服从标准正态分布，且I中各节点之间相互独立，考虑到权值矩阵的各值均来自同一分布因而方差相等，则有

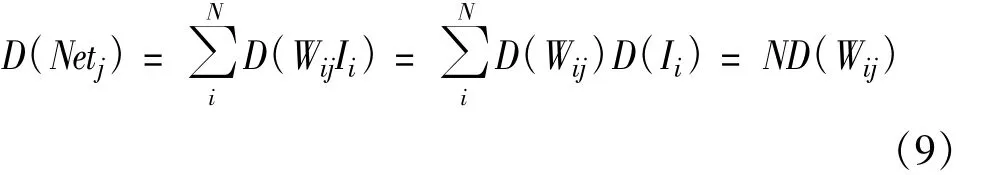
因而，若权值矩阵初始化为服从高斯分布的数据，则逻辑斯谛函数自变量也服从零均值的高斯分布，且方差为上述方差的N倍。反之，如果确定了Netj的方差，则权值的方差也随之确定。

图2为Netj值的sigmoid二阶导数及高斯分布函数图。

图2Netj值的sigmoid二阶导数及高斯分布函数图Fig.2 The sigmoid second derivative and Gauss distribution figures of Netj

由于参数值的初始化对精度的要求并不高，因而此问题可以通过蒙特卡罗（Monte Carlo）方法解决。本文得出的该值近似在D＝1.392左右。

因而，在预训练的过程中，将RBM做如下的参数初始化：

（1）两层的阈值均设为全0向量；

4 实验及结果

为了验证上述算法的正确性，从总长为51.1 h的大数据集中随机选取了70 000帧语音数据。对每帧提取45维的MFCC相关特征和4维的音调特征，总计49维。每一帧输入神经网络进行计算时，将其前后各5帧的数据连同其本身作为一个数据窗口，即窗长为11。这样的做法可以让网络不仅学习当前帧的信息，也能同时利用帧间的关系，这也被认为是神经网络能够超越GMM-HMM模型的关键点之一。根据上述设定易知实验中所采用的RBM输入层大小为N＝49×11＝539，输出层大小参考目前常用的做法，设为2 048。

本文利用MATLAB实现了预训练和参数值初始化的验证，在同一学习速率下，设定不同的权值矩阵初始化方差，每种不同情况对数据集循环训练10次。为了降低每次输入的数据量过少给更新带来的抖动，将100帧数据作为一批输入网络，计算误差后对所有参数进行一次更新，因而在10次循环后共有7 000个平均重建误差值。将不同方差下的误差曲线归一化到［0，1］的范围内比较其收敛的快慢，其对数值随数据批次n（n为1～7 000）变化的结果如图3所示，此处所用的学习速率为3.0×10－6。

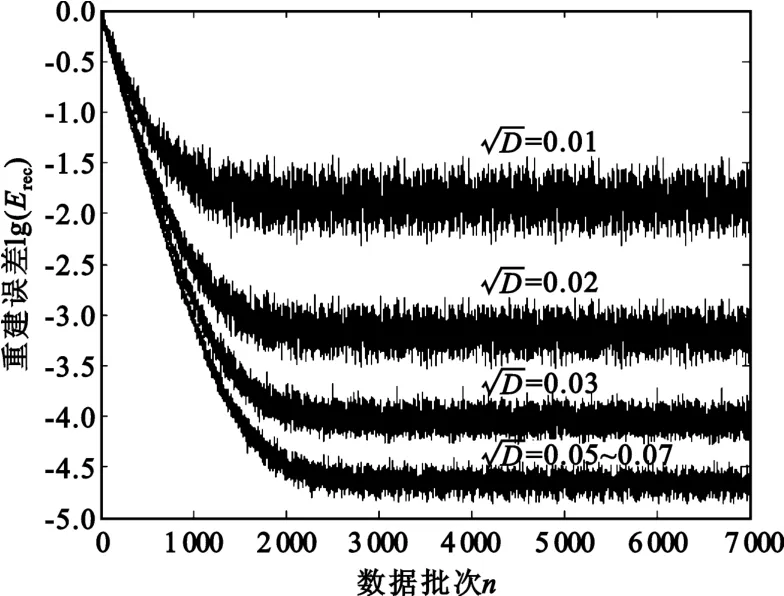
图3 重建误差对数值下降曲线Fig.3 The logarithmic decline curve of reconstruction error

图3中4条由上至下的误差曲线分别表示了Netj的分布标准差为0.01、0.02、0.03、0.05～0.07的情况，而通过前述理论计算出的理想标准差为

可以看出，方差在理论值附近的曲线下降速率更快，但只根据此图对该理论范围内的收敛速度不好比较。为了更直观地得到这一结果，计算了归一化后各误差曲线中所有数据点的平均值，该值越小，说明相对于开始时的误差，后续的训练中误差值下降得越快，其对数值曲线如图4所示，所用的学习速率与图3中相同。可见在0.05～0.06的范围内，曲线达到了最小值，说明此时的收敛速度较快。

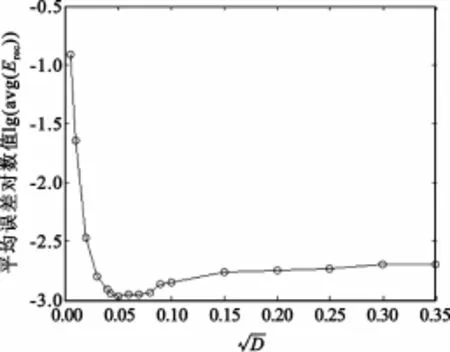
图4 重建误差平均值随Netj标准差的变化曲线Fig.4 The logarithmic curve of average reconstruction error by standard deviation of Netj

为了排除训练时学习速率对实验结论可能带来的影响，本文比较了不同学习速率下图4中曲线的变化趋势，其结果如图5所示。其中竖直虚线对应的横轴坐标即为上述最佳标注差0.059 9。此图说明，在不同的学习速率下，取该标准差均能达到几乎最好的收敛速度，从而验证了本文第3部分提出的理论。

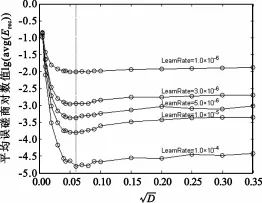
图5 不同学习速率下误差均值随标准差的变化曲线Fig.5 The logarithmic curve of average reconstruction error by standard deviation in vary learning rates

5 结束语

本文主要利用了神经网络传递过程中激励函数的非线性区域，以及输入数据服从高斯分布的特性，提出了一种初始化权值的方法。实验表明，该初始化方式能够使训练的收敛速度提升，并为其他形式数据分布或其他形式激励函数下的神经网络训练提供了一种初始值确定的分析方式。当然，激励函数的存在并不仅仅是为了提供非线性的关系，其线性部分也是数据逐层传递的过程中非常重要的可利用区间。在今后的课题研究中，还要进一步考察网络对不同区域的利用方式，探索新的提升速度的办法。

［1］Mohamed A，Dahl G，Hinton G.Deep belief networks for phone recognition［C］／／NIPS Workshop on Deep Learning for Speech Recognition and Related Applications.Whistler，BC，Canada：［s.n.］，2009：1－6.

［2］Mohamed A，Hinton G，Penn G.Understanding how deep belief networks perform acoustic modeling［C］／／Proceedings of 2012 IEEE International Conference on Acoustics，Speech and Signal Processing.Kyoto：IEEE，2012：4273－4276.

［3］Dahl G E，Yu D，Deng L，et al.Context-Dependent Pre-Trained Deep Neural Networks for Large-Vocabulary Speech Recognition［J］.IEEE Transactions on Audio，Speech，and Language Processing，2012，20（1）：30－42.

［4］阎平凡，张长水.人工神经网络与模拟进化计算［M］.北京：清华大学出版社，2005. YAN Ping-fan，ZHANG Chang-shui.Artificial Neural Network and Evolutionary Computation［M］.Beijing：Tsinghua University Press，2005.（in Chinese）

［5］Hinton G.A practical guide to training restricted Boltzmann machines［J］.Momentum，2010（9）：1－20.

［6］LeCun Y，Bottou L，Orr G B，et al.Efficient backprop［M］／／Neural networks：Tricks of the trade.Heidelberg，Berlin：Springer，1998：9－50.

ZHOU Jia-jun was born in Baoding，Hebei Province，in 1989.He received the B.S.degree in 2010.He is now a graduate student.His research direction is speech recognition.

Email：zhoujiajun06＠gmail.com

欧智坚（1975—），男，湖南衡阳人，2003年获博士学位，现为副教授，主要研究方向为语音识别与机器智能。

OU Zhi-jian was born in Hengyang，Hunan Province，in 1975.He received the Ph.D.degree in 2003.He is now an associate professor.His research direction is speech processing and machine intelligence.

Improved Initialization of Pre-Training in Deep Neural Network

ZHOU Jia-jun，OU Zhi-jian
（Department of Electronic Engineering，Tsinghua University，Beijing 100084，China）

Second derivative of activation function is used to optimize weight initialization in deep neural network pretraining phase within speech recognition tasks.By using the non-linear region of activation function and independent variables′Gaussian distribution，a method of finding the best variance is proposed in order to speed the training up. Comparison of convergence rates in different weight initialization at the same learning rate shows that this method can accelerate the speed of the pre-training phase and enhance the efficiency of neural network training.

speech recognition；deep neural network；pre-training；initialization；activation function

The National Natural Science Foundation of China（No.61075020）

date：2013－04－18；Revised date：2013－05－10

国家自然科学基金资助项目（61075020）

❋❋通讯作者：zhoujiajun06＠gmail.comCorresponding author：zhoujiajun06＠gmail.com

TN912.3

A

1001－893X（2013）07－0895－04

文献［2］的说法，预训练的过程实际是最大化了数据的似然值，从而期望模型参数向着数据分布的方向靠拢，从而使BP算法在已知数据分布的情况下，最大化标注的后验概率时相对更容易。而根据文献［3］的结果，预训练可以将深层神经网络的识别准确率提高几个百分点。

周佳俊（1989—），男，河北保定人，2010年获学士学位，现为硕士研究生，主要研究方向为语音识别；

10.3969／j.issn.1001－893x.2013.07.014

2013－04－18；

2013－05－10