三相电压型PWM整流器分数阶PID直接功率控制

王璇 ，张小凤 ，周丰 ，张海霞

（1.嘉兴学院 南湖学院，浙江 嘉兴 314001；2.华南理工大学 自动化科学与工程学院，广东 广州 510641；3.嘉兴学院 机电工程学院，浙江 嘉兴 314001；4.秦皇岛电力公司，河北 秦皇岛 066000）

1 引言

三相电压型PWM整流器具有可实现网侧电流正弦化、单位功率因数运行、能量双向传输、动态响应快等优点，其电流控制策略在工程实际中得到了普遍研究和应用，但直接电流控制结构复杂，间接电流控制动态特性较差［1］，为了满足非线性电力电子装置控制需要，提出适用于非线性系统的直接功率控制方法［2］（DPC）。 直接功率控制从能量的角度出发间接控制了瞬时电流，通过控制有功和无功在允许范围内来调整电流在允许范围内，对于暂态和非线性条件下的三相PWM整流器控制更加合理和有效，而且算法和系统的结构简单，具有更高的功率因数，低的THD。

本文在瞬时功率理论的基础上研究了直接功率控制算法，设计了功率控制内环、直流电压外环的控制结构，将瞬时功率与参考值的差值送入滞环比较器，根据交流源电压及瞬时功率在开关表中对应选择整流器输入电压的控制开关量，迫使实际有功跟上给定。本文电压外环采用分数阶 PIλDμ控制器（FOPID）得到有功给定， 根据直流母线电压的实际值与参考值之间的误差来控制从电网吸收或释放有功电流的值，从而保证总的能量平衡，稳定直流母线电压。仿真实验结果证明，基于分数阶PIλDμ控制器的直接功率控制方法能够有效地控制三相电压型PWM整流器，实现网侧电流正弦化及小的谐波含量，并且直流侧电压的分数阶PIλDμ控制方案明显优于传统PI控制（IOPI）方案，具有良好的动态性能和较强的鲁棒性，响应速度更快，控制结果更精确。

2 基于分数阶PID的直接功率控制系统

三相电压型PWM整流器DPC系统如图1所示。主电路由交流电源、滤波电抗器、整流器、直流电解电容器、负载组成；控制电路为直流电压外环功率内环结构；由交流电压、电流检测电路和直流电压检测电路，功率估算器，扇形划分器，功率滞环比较器，开关表及PI调节器组成。

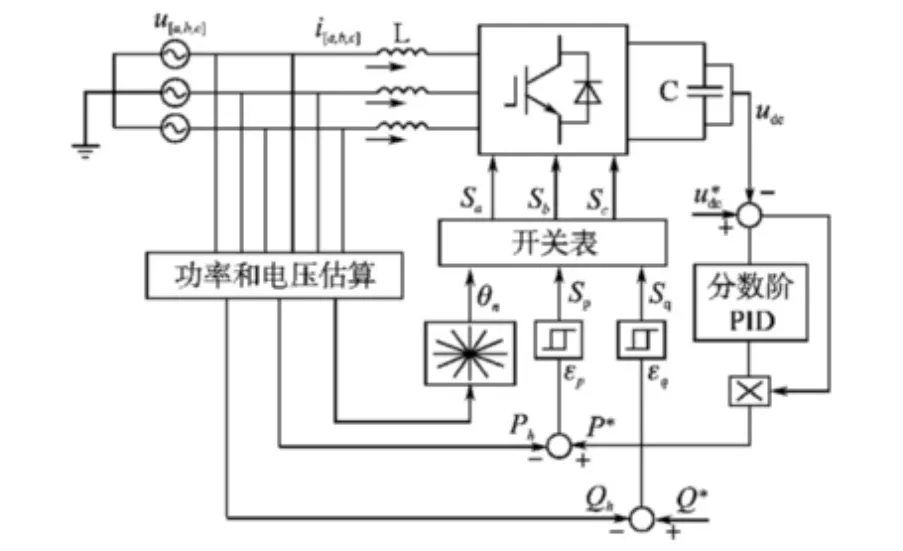
图1 PWM整流器基于分数阶PID的DPC控制系统Fig.1 PWM rectifier DPC control system based on fractional-order PID

瞬时有功功率与无功功率根据检测到的电流 ia，ib，ic及电压 ua，ub，uc进行计算，瞬时有功功率为电压矢量与电流矢量的标量积，瞬时无功功率为电压矢量与电流矢量的矢量积。首先转换到αβ坐标系，然后按照下式得到瞬时有功和无功功率的估算值P，Q：

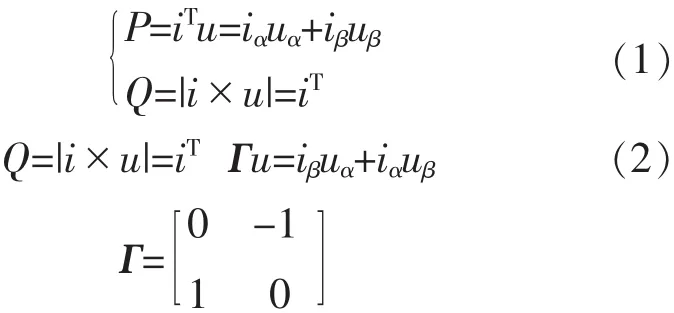
检测到的实际功率P和Q与给定的Pref和Qref比较后可以得到功率跟踪差值εP，εQ，参考值Pref由直流电压外环设定，参考值Qref设置为0。εP，εQ为滞环比较器的输入，其输出为反映实际功率偏离给定功率的状态的 SP，SQ信号，SP，SQ只有0和1这2种状态，按下列规则确定：

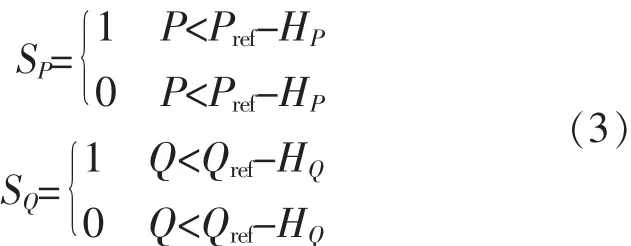
其中HP，HQ为有功和无功功率滞回比较器的滞回宽度，HP，HQ决定了功率控制精度，亦决定了开关频率。

开关表是根据SP，SQ及电压所在的扇区θn的组合确定DPC系统所需的开关状态的，即Sa，Sb，Sc的取值，驱动主电路对应开关管。开关状态SaSbSc=000～111 对应于 U0～U7，即 U0（000），U1（100），U2（110），U3（010），U4（011），U5（001），U6（101）， U7（111）， 其中 U0（000）和 U7（111）位于原点。开关表见表1。

表1 功率控制开关表Tab.1 Switching table of power control

电压所在扇区θn可以通过计算得到，将检测到的电压 ua，ub，uc变换到 αβ 坐标系下的分量 uα，uβ送入扇形选择器，计算 θn=arctan（uα/uβ），且（n-2）π/6≤θn≤（n-1）π/6（n=1，2，…，12），将电压空间矢量在 αβ 坐标系中划分为 12 个扇区（θ1～θ12），其分布如图2所示。

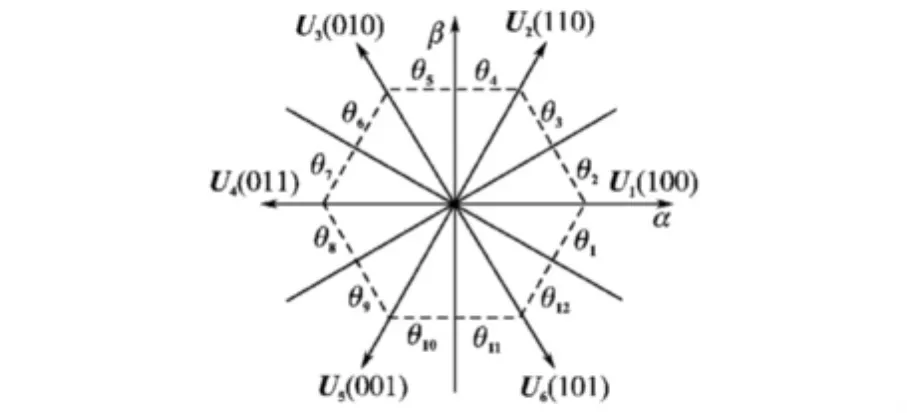
图2 电压空间矢量图Fig.2 Space vectors of voltage

如前所述，传统三相PWM整流器直流侧电压采用整数阶PI控制器进行控制，虽然可以满足一定范围内的控制要求，但是系统参数变化时波动比较大。针对PID调节器存在的问题，本文将分数阶控制器引入直流侧电压控制，分析基于分数阶控制器的直流侧电压控制的动态响应特性和鲁棒稳定性。

3 基于瞬时功率理论的三相电压型PWM整流器

三相电压型PWM整流器主电路结构见图3。

图3 三相电压型PWM整流器主电路结构Fig.3 Main circuit of three-phase voltage type PWM rectifier

对直流侧应用基尔霍夫第一定律，由图3得

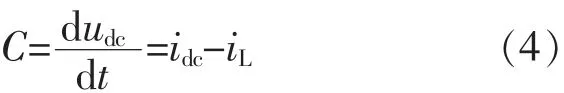
其中

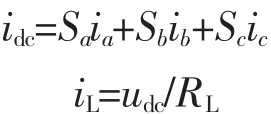
当不考虑桥路开关损失，系统工作于稳态且处于单位功率因数整流状态，根据式（4）可得瞬时有功功率为

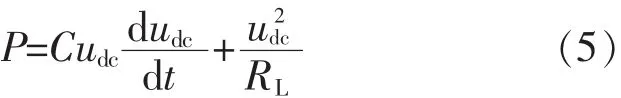
设 udcr=udc+△udc，可得

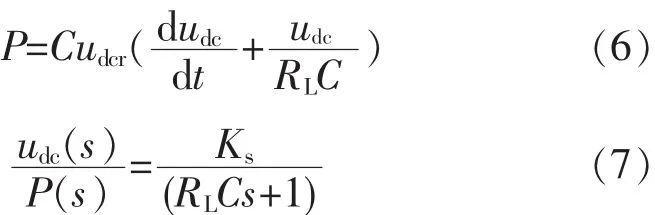
其中，Ks=RL/udcr由于功率内环滞环PWM开关频率比较高，则功率内环可用一个小惯性环节代替，即

式中：Tp为功率内环等效时间常数。

根据以上分析，得到DPC控制系统结构如图4所示，图4中Gfo（s）为电压调节器传递函数。由图4可知，Pref=udcifo，ifo是分数阶PID调节器的输出，在DPC 系统稳态运行时，udc=udcr+△udc≈udcr。

图4 整流器DPC系统控制结构Fig.4 Control structure of rectifier DPC system

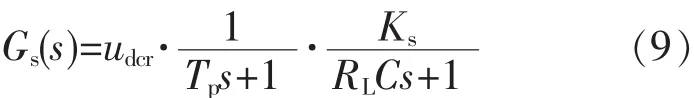
系统开环传递函数为

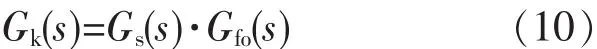
被控对象传递函数为

4 分数阶PID控制器的设计

分数阶微积分在控制中得到应用，产生了分数阶控制理论与分数阶控制器，通过适当调整控制器参数可以得到更为理想的控制效果。Podlubny教授提出了分数阶PIλDμ控制器，并精确地分析了分数阶控制系统的动态响应，得到分数阶控制被控对象可取得比常规PID控制器更好的控制性能的结论［4］。PIλDμ控制器除了有 Kp，Ki，Kd3个参数，还有积分阶次λ和微分阶次μ 2个为任意实数值的可调参数，参数的可调范围扩大，能够更精确地控制受控对象。分数阶PIλDμ控制器的传递函数为

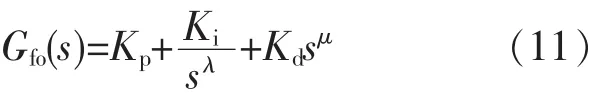
可以根据控制系统的设计指标对分数阶PIλDμ控制器的参数进行计算，得到对应的参数 Kp，Ki，Kd，λ，μ。

根据式 （11）得到分数阶 PIλDμ控制器的频率响应为

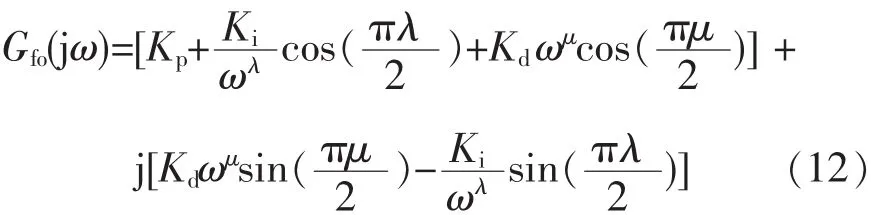
分数阶PIλDμ控制器相角和增益为

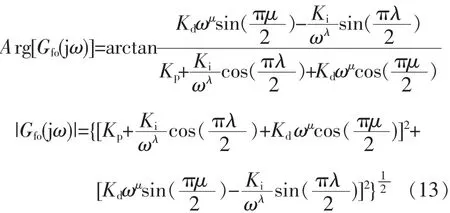
根据式（9），被控对象频率响应为

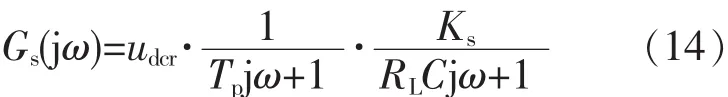
被控对象Gs（s）的相角和增益为

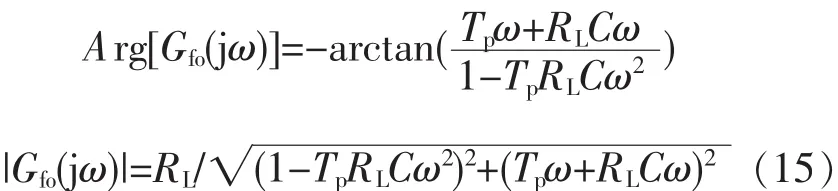
由式（10）知系统开环频率响应及其相角和增益为

根据幅值裕量Am和相位裕量φm指标［5］，系统参数之间应满足如下关系：

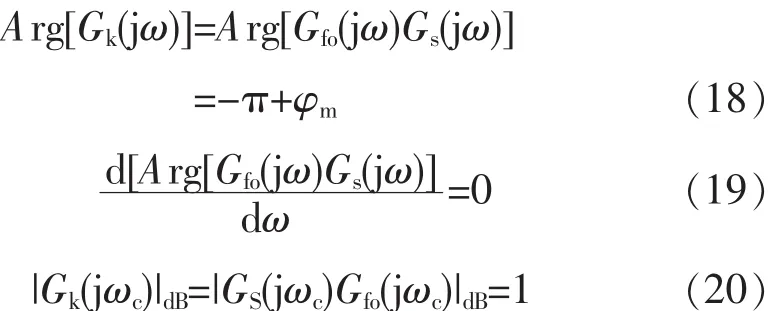
本文根据经验将阶次λ和μ限定在［0.1，1.5］范围之内，在这个范围之内不断变换两阶次取值，结合方程组式（18）、式（19）、式（20）得到相应的控制器的参数。λ和μ的不同组合下取使得ITAE值最小时的阶次取值设计分数阶PID控制器［6］，此时赋值 udcr=700 V，φm=50 °，ωc=10 rad/s，微积分的阶次为λ=0.8，μ=0.3。代入组合方程组，得到Kp，Ki，Kd，得到的分数阶 PID 控制器为

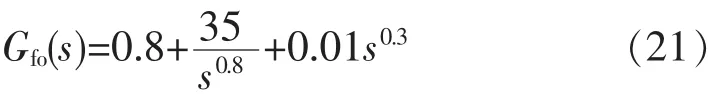
5 Oustaloup近似算法

Oustaloup算法是常见的用整数阶系统对Laplace算子sα的近似拟合的方法，相当于用多级整数阶滤波器串联对算子进行频域近似。因而任意函数 f（t）的分数阶数值微积分相当于 f（t）经该滤波器后的输出［7］。

假定选定的拟合频率段为（ωb，ωh），则可以构造出多级滤波器串联的传递函数模型：

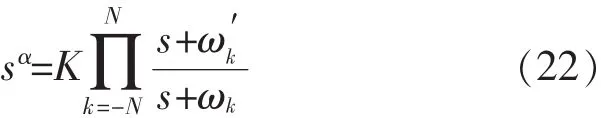
相应参数可由下式给出：

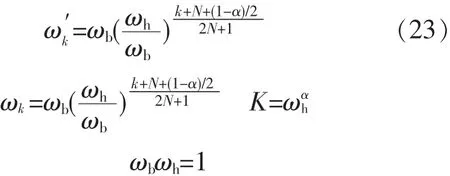
转折频率 ωk′，ωk时的设定决定了 Laplace算子 sα的精确近似拟合。得到算子的拟合式后，便可以在仿真软件中实现分数阶控制器的计算机仿真，进行控制效果分析。

6 仿真结果及分析

在Matlab/Simulink中建立三相PWM整流器的系统仿真模型。电网相电压幅值为220 V，频率为50 Hz，整流器输入侧串入电感LL=1 mH，输出侧并接电容C1=3000 μF，并接在电容两端的电阻RL=20 Ω作为整流器的负载。图5～图12为三相电压型PWM整流器基于分数阶控制器的仿真波形。

图5是在IOPID控制下的整流器网侧电压和电流波形，由图5可知电流接近正弦，电压和电流同相，实现单位功率因数，谐波含量小。图6为谐波分析结果，THD值为3.75%，低于5%。

图5 IOPID控制器下网侧电压电流波形Fig.5 Grid voltage and current under IOPID controller

图6 网侧电流谐波分析Fig.6 Harmonic analysis of grid current

图7为IOPID和FOPID控制器下直流侧电压波形。由图7可知在FOPID控制下，直流侧电压的超调更小，控制更加准确，更加快速地达到给定电压700 V，实现无静差控制。

图7 IOPID和FOPID控制器下直流侧电压波形Fig.7 DC voltage with IOPID and FOPID controller

图8为整流器负载变化时的网侧电压和电流波形，时间从0.2 s至0.3 s时段电阻由20 Ω变为10 Ω，由电流波形可见负载减小电流变大，且变化过渡快速平缓，不会给系统带来冲击。图9为相同情况下的直流侧电压变化情况，FOPID控制下，电压恢复快，受影响小，鲁棒性较强。图10为局部放大波形。

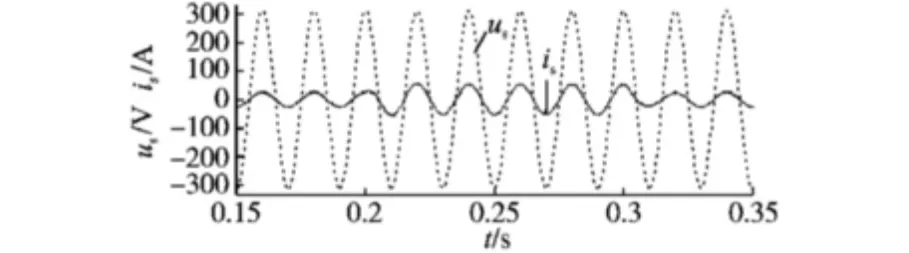
图8 负载变化时整流器网侧电压和电流波形Fig.8 Rectifier grid voltage and current waveforms when load change

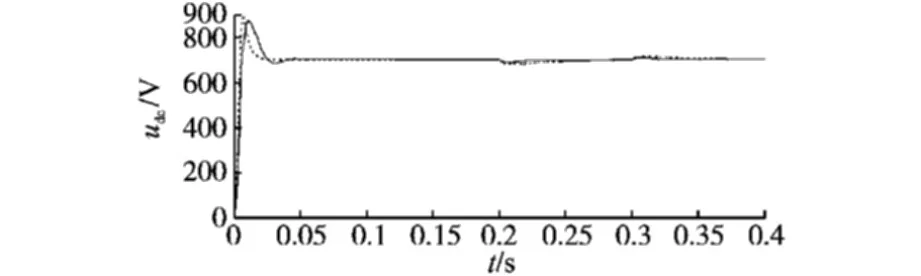
图9 负载变化时的直流侧电压波形Fig.9 DC voltage waveforms when load change

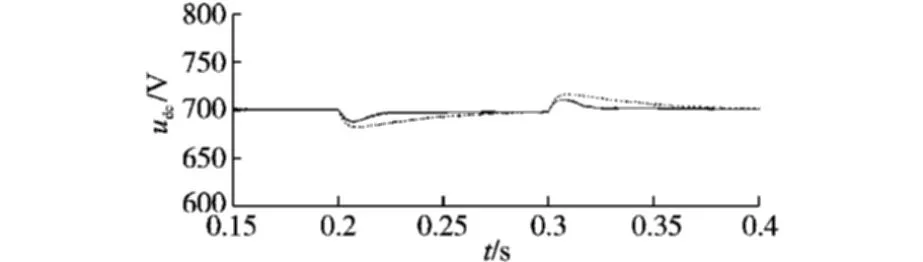
图10 负载变化时的电压波形局部放大图Fig.10 Partial enlarges of DC voltage when load change

图11为整流器在电压冲击情况下网侧电压和电流波形，时间从0.2 s至0.22 s时段电压变为1.2倍，时间从0.3 s至0.32 s时段电压变为0.8倍，可见分数阶控制下，电压冲击和瞬时波动对电流的变化和直流侧电压变化影响不大，对参数变化不敏感，鲁棒性更强。图12为FOPID控制器下直流侧电压波形的局部放大图，由图12可知在FOPID控制下，直流侧电压的超调更小，稳定时间短，控制更加准确。

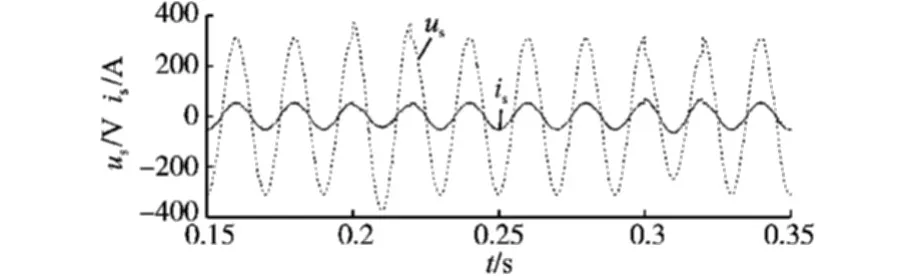
图11 电压冲击时直流侧电压波形Fig.11 DC Side voltage waveforms when voltage change

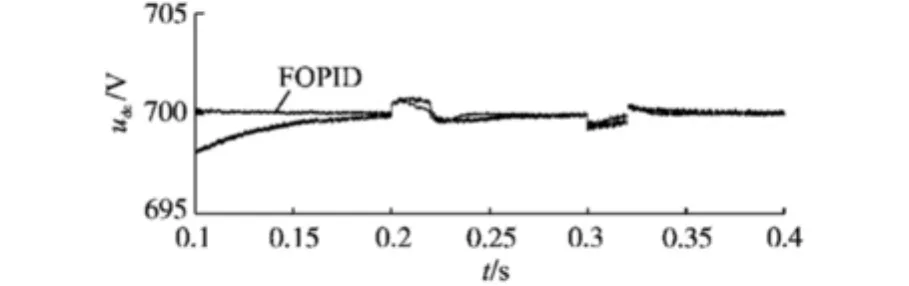
图12 电压冲击时电压波形局部放大图Fig.12 Partial enlarges of DC voltage when voltage change

7 结论

本文基于瞬时功率理论，分析了三相电压型PWM整流器的功率模型，设计了直接功率控制系统，并且在负载变化和电网波动情况下跟踪控制，保证了三相电压型PWM整流器的性能并降低其损耗。针对直流侧电压控制设计了分数阶PIλDμ控制器，对其特性、参数整定和控制性能等方面进行了分析研究。仿真结果分析证明了基于分数阶PIλDμ的直接功率控制能够实现三相电压型PWM整流器的控制效果，网侧电流接近正弦，功率因数单位化，而且分数阶PIλDμ控制器对系统参数变化不敏感，直流侧电压能够快速稳定在给定值，控制精确，具有更强的鲁棒性。

［1］张笑微，李永东.幅相控制PWM变流器电流谐波分析及参数选择［J］.电力电子技术，2003，37（4）：13－15.

［2］王久和，李华德，王立明.电压型PWM整流器直接功率控制系统［J］.中国电机工程学报，2006，26（18）： 54－60.

［3］唐雄民，朱燕飞.三相恒频PWM整流器的直接功率控制研究［J］.电气传动，2011，41（11）：32－37.

［4］Podlubny I.Fractional-order Systems and Controllers［J］.IEEE Transactions on Automatic Control，1999，44（1）：208－214.

［5］薛定宇，赵春娜.分数阶系统的分数阶PID控制器设计［J］.控制理论与应用，2007，24（5）： 771－776.

［6］赵春娜，赵雨，张祥德，等.分数阶控制器与整数阶控制器仿真研究［J］.系统仿真学报，2009，21（3）： 768－775.

［7］梁祖权，束洪春.新型 UPQC 直流电压的 PIλDμ控制［J］.电工技术学报，2010，25（2）：147－157.