等分分层组合投影研究

任留成，吕泗洲

（1.空军指挥学院，北京 100097）

地图投影是用有限的平面表示地球曲面上的地理要素而进行的拓扑变换。探求地图投影的原理和方法一般有4种：按投影的变形性质探求地图投影方法，按投影的经纬线形状探求地图投影方法，按投影的变形分布探求地图投影方法，按投影的其他条件探求地图投影方法[1]。这些方法都选择单一的柱面、锥面或切（割）平面作为投影面，有的在某些地区变形较大，有的因为分带表示而不能保证全球地理数据的连续表达。为了“数字地球”和大型GIS的深入发展，必须为其建立较理想的数学基础。

本文针对中国地理格网（多级格网系统）的分割方法[1-4]，设计建立一种适合该格网系统的新型地图投影——分层组合投影。本文选择地球椭球模型为克拉索夫斯基椭球，采用微分几何方法，把地球椭球分割成若干层圆台，分别建立每个圆台各不相同的分层组合投影模型。这种投影还可根据格网间隔的不同进行细分，从而发展成为一种适合多分辨率格网模型的动态地图投影，使之可以扩展成为“数字地球”和大型GIS的理想的数学基础。

1 几何模型

该投影的设计思路是：从赤道面开始，把地球南北半球按等纬度分成若干层，每一层对应于地球椭球体的一个圆台，顶层是一个球冠。为了计算简单起见，在精度范围内，我们采用不等厚度分割，即近赤道地区分割带要宽一些，高纬度地区变窄。对于每一个圆台，假想有个圆柱在底圆与之相切，依此建立局部等角圆柱投影；对于顶层的球冠，可以设计等角方位投影。如图1所示。

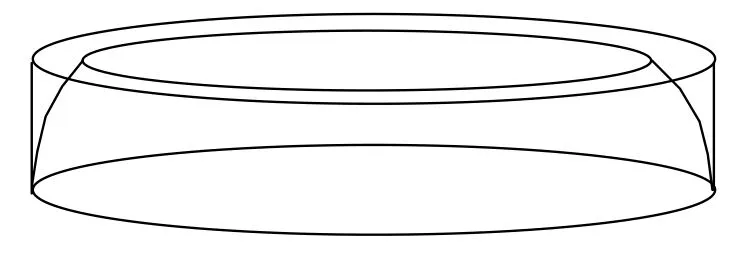
图1 圆柱逼近圆台

2 分层投影模型

设地球旋转椭球方程为：

式中，a、b为地球椭球的长短半轴。按照纬度每i度分割为一层（如i=1,3,6,10等），把上下半球各分割成J=90/i层，每一层的地球表面都用一个柱面近似表示，此时地球的模拟实体如图2所示。下面仅讨论上半球。

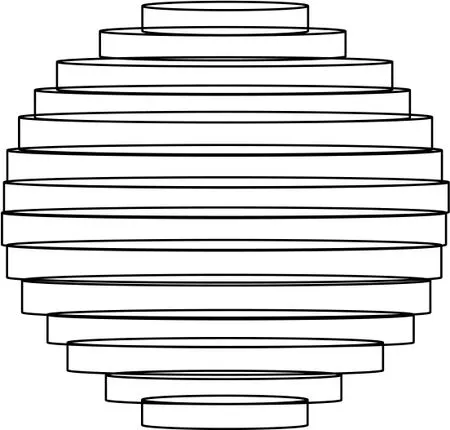
图2 地球模拟形状

1）第1层，起层为赤道（纬度B11=0°），末层为纬度B12=i°，相应的曲边圆台同胚于一个圆柱，如图2所示，该圆柱体的方程为：

该圆台与其相应的圆柱之间的等角圆柱投影可采用Mercator投影，公式为：

式中，LB表示经纬度；l代表经差，l=L-L0；L0为中央经线。

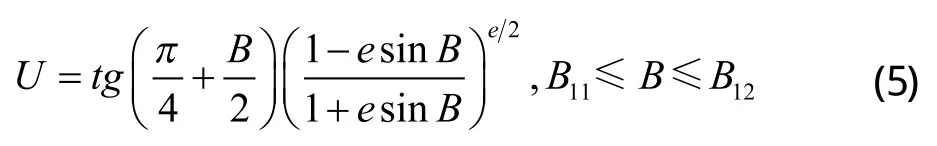
2）对于第2层，起层的纬度为B21=i°，末层为B22=2i°，如图3所示，r=NcosB21，其中则第2层是圆柱体。

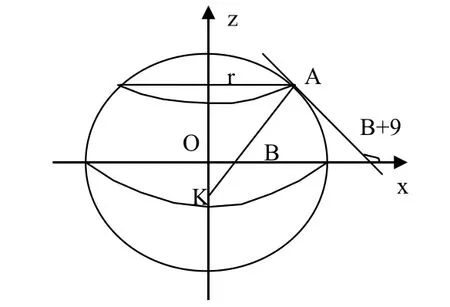
图3 椭球截面图

在B21=i°处与圆台相切，则相应于该层的等角圆柱投影公式为：

式中，U的表达式如式（5）所示，B21≤B≤B22。

3）对于第j层(j=3,4,…,J-1)，起层的纬度为Bj1=（j-1）·i°，末层为Bj2=j·i°，根据图3，r=NcosBj1，其中则第j层是圆柱体。

然而，知识型员工作为知识存储、传递、创造的主体在企业中获得了更加主动的地位，这不仅体现在劳资双方的博弈过程中，也同样体现在企业的管理方式和企业文化的选择中。由于知识型员工对某一具体企业的经济依附性下降，能够凭借其拥有的技术、知识在劳动力市场中获得更多的发展机会，因而，现代企业往往面临着核心知识员工流失的困境。在知识密集、创新导向的企业中，知识员工的流失给企业造成的损失十分巨大，甚至会削弱企业的核心竞争能力。

在Bj1=（j-1）·i°处与圆台相切，则相应于该层的等角圆柱投影公式为：

式中，U的表达式如式（5）所示，Bj1≤B≤Bj2。

4）对于顶层的球冠，起点的纬度为BJ1=（J-1）·i°，终点为BJ2=90°，可利用等角正方位投影模型来表述，公式为：

式中，ρ=2Rtan(z/2)；δ=l。

3 分层投影的整体组合

图2中的每一个圆台表面都是一个环形带，把这个环形带以某一条经线（比如L=0）为基准分割开，然后投影到平面上，就是一个矩形；再把每个矩形带按照相邻层次依次排列在同一平面内，则合并成整个地球表面的一种条形投影，如图4所示。

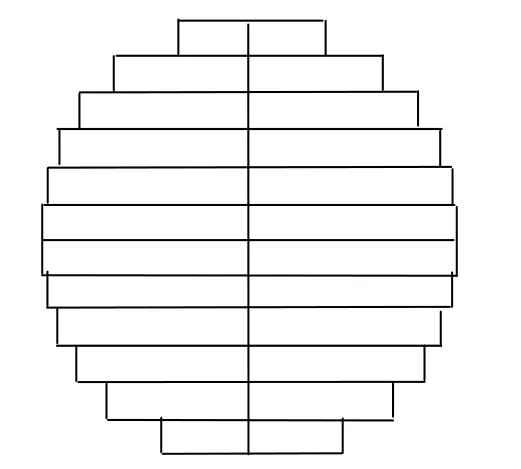
图4 全球投影

为了保证各个条带地图投影坐标的连续性，实现上下条带之间的无缝衔接，本文提出一种新的无缝衔接变换方法，使得相邻2条带在分界线上每个点的位置坐标完全一致。

下面构造一种变换，该变换满足以下特性：①把矩形ABCD变换为梯形DA1B1C（如图5所示）；②把线段AB变换为A1B1;③保持CD不变;④保持CD平行于A1B1。

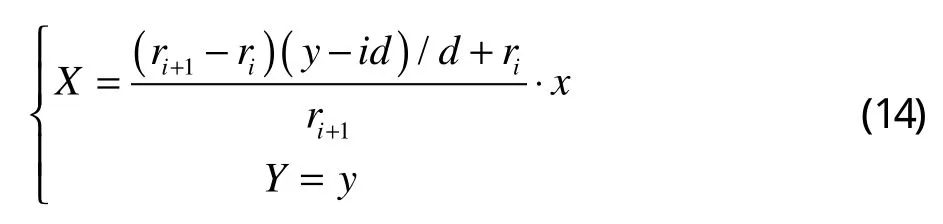
则该变换满足上述特性，它把图5的两个相邻矩形的其中一个变换为梯形。

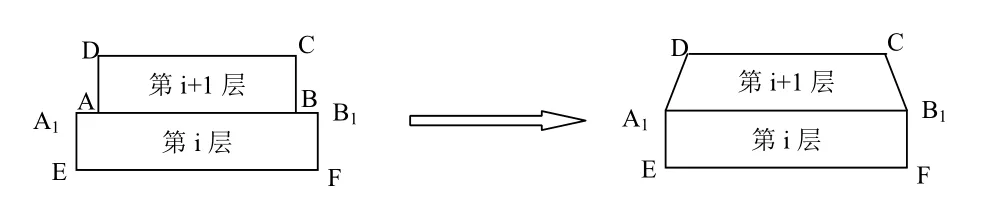
图5 相邻两层的衔接变换

依此类推，把图4中除赤道两侧的其他矩形条都变成了梯形，就实现了分层坐标的无缝衔接；再把第3部分得到的投影坐标公式按分段函数的方法组合在一起，则得到整个地球表面的投影公式为：

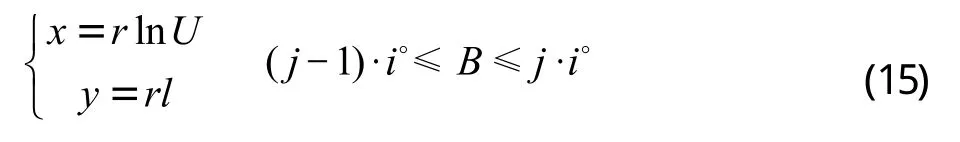
4 变形分析

因为是等角投影，所以只考虑长度变形和面积变形。

1)长度变形。子午线求法为：

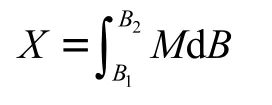
最后，经过整理可得到由赤道起算的子午线弧长：

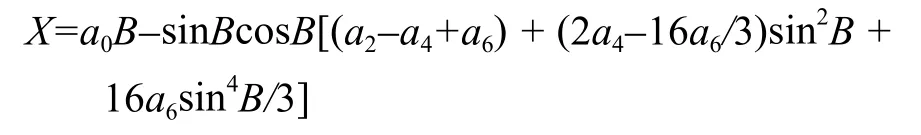
对克拉索夫椭球，得：

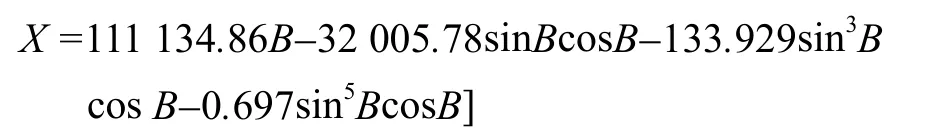
利用此公式，可求得所需弧长。由子午线公式x2/a2+z2/b2=1可得：

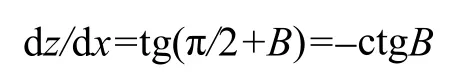
考虑x与z的绝对值变化的情况：

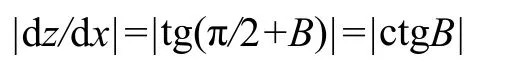
在BÎ[0,π/2]范围内，随着纬度越高，z随x的变化就越慢；则纬线弧长随纬度值的增大相对z就变化得越快。因此，子午线方向上，长度变形随着纬度增加而增大。长度比公式为：

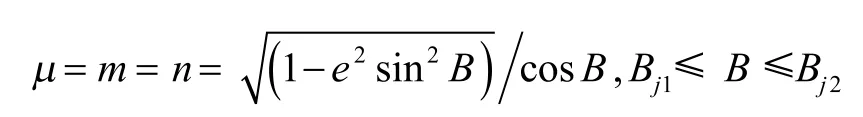
2）面积变形。面积比公式为：

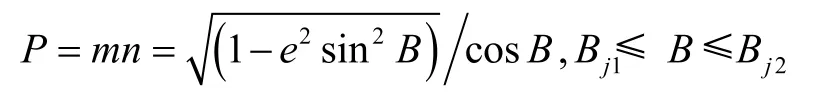
所以，长度变形为μ-1，面积变形为P-1。经计算得出变形结论如下：

1°分层：0°～88.9°之间的长度最大变形为 0.817 23，面积最大变形为2.304 844；而Mercator投影在0°～56.7°之间长度最大变形达到0.821 389，面积最大变形达到2.317 459，在88.9°处长度最大变形高达52.088 987，面积最大变形高达2 713.262 584。表1仅列出部分纬线上的长度变形和面积变形。

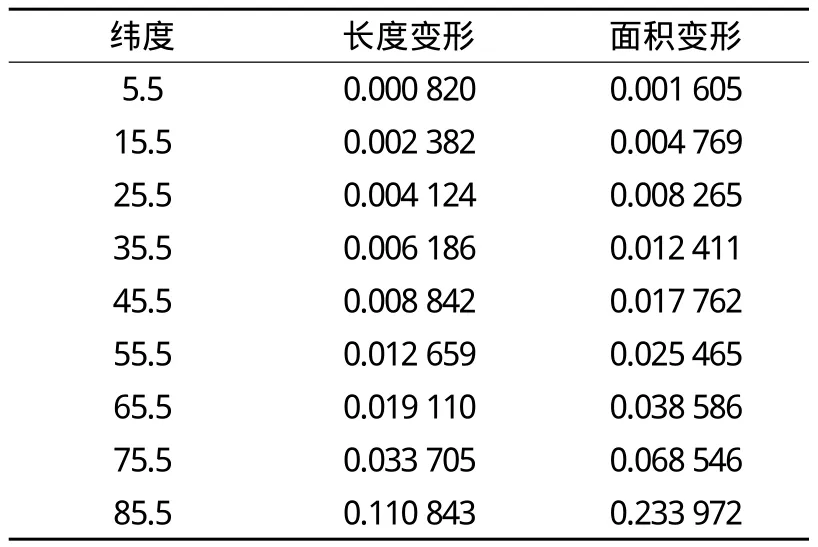
表1 1°分层部分纬线上的长度变形和面积变形

3°分层：0°～88.9°长度最大变形为1.726 192，面积最大变形为6.432 121，它几乎是Mercator投影在68.5°附近的精度。表2列出部分长度变形和面积变形。

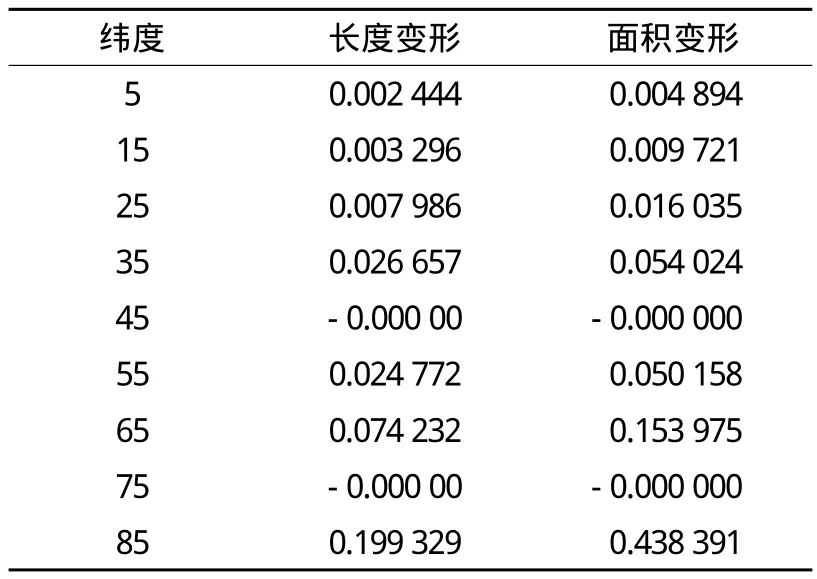
表2 3°分层部分长度变形和面积变形

10°分层：0°～85°长度最大变形为0.992 388，面积最大变形为2.969 610，它几乎是Mercator投影在60°附近的精度。表3列出部分长度变形和面积变形。

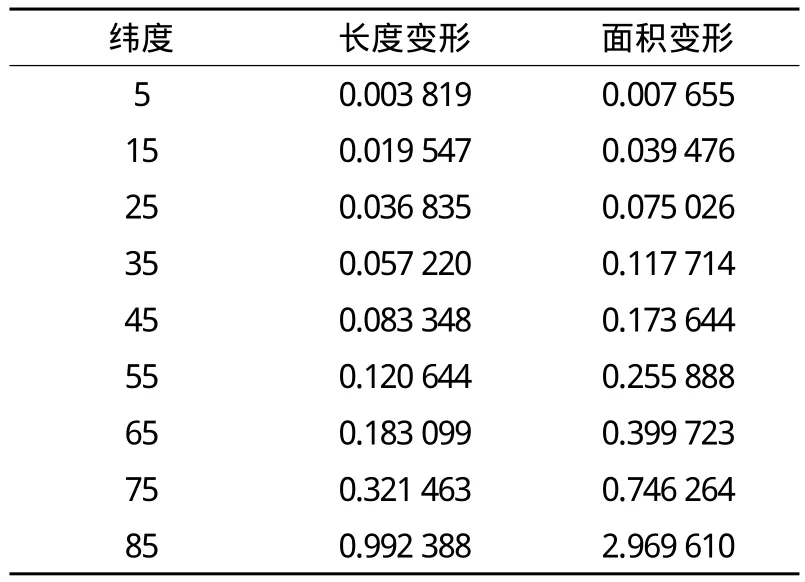
表3 10°分层部分长度变形和面积变形

[1]杨启和. 地图投影变换[M]. 北京：解放军出版社，1992

[2]胡鹏. 地图代数[M]. 武汉：武汉大学出版社，2000

[3]李国藻，杨启和，胡定荃. 地图投影[M]. 北京：解放军出版社，1989

[4]国家测绘局. GB/T 12409-2009 地理格网[S]. 北京：中国标准出版社，2009

[5]任留成. 空间投影理论及其在遥感技术中的应用[M]. 北京：科学出版社，2003

[6]袁文，马霭乃，管晓静. 一种新的球面三角投影：等角比投影 [J]. 测绘学报，2005， 34(1)：81-87

[7]Ren Liucheng, Clarke Keith C, Zhou Chenghu, et al. Geometric Rectification of Satellite Imagery with Minimal Ground Control Using Space Oblique Mercator Projection Theory[J].Cartography and Geographic Information Science，2010，37(4)：10-16

[8]李家，赵晴晴. 等差分纬线多圆锥投影正解变换的参数和方法[J]. 地理空间信息，2012，10（2）：38-40

[9]赵建辉. 地图投影在《新疆资源经济地图集》中的设计[J].地理空间信息，2012，10（2）：161-162