椭圆柱相贯线槽的数控加工

刘振超

（柳州铁道职业技术学院，广西 柳州545007）

凸轮是汽车、内燃机、工程机械、机械制造等行业广泛应用的关键零件之一，其种类繁多，型面复杂。许多凸轮零件的轮廓曲线是较为复杂的非圆曲线，如渐开线曲线、抛物线等，目前多用UG、Mastercam等软件或CAD/CAM集成系统进行自动编程和加工，但这种方式存在数控程序长、灵活性不足等问题。如果采用宏程序编程，则这些问题将会得到很好的解决。宏程序使用变量编程，能够对变量进行赋值，同时变量间还可以进行算术与逻辑运算，可将有规律的形状用最短的程序段表示出来，编写出的程序非常简洁，逻辑严密，通用性极强，具有极好的易读性和修改性，而且机床在执行此类程序时，比执行CAD/CAM软件生成的程序更加快捷，反应更迅速。特别对于中等难度的零件，使用宏程序加工要比自动编程效率更高。本文以柱形端面凸轮曲线槽的编程和加工为例，详细解析了宏程序的应用。

1 建立曲线槽的数学模型

图1是一柱形端面凸轮，椭圆1柱体已完成加工，其AMBA曲线为一空间曲线槽，其曲线是由两个相互垂直的椭圆柱1、2正交形成的相贯轮廓线。当凸轮绕回转中心O1O2轴回转时，通过该曲线槽轮廓控制与它配合的摆杆的运动。

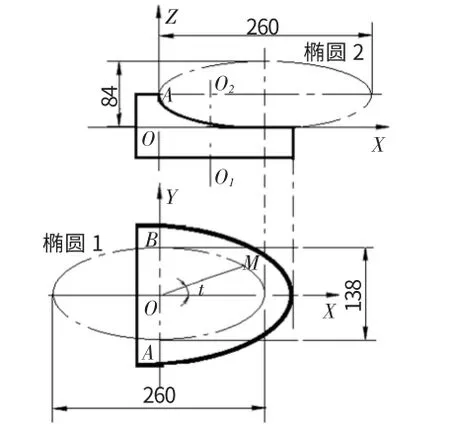
图1 柱形凸轮端面曲线及工件坐标系

该曲线槽在XOY平面上的投影是1/2椭圆及一条连接直线。考虑到取值计算的方便，以椭圆1的对称中心O为零点建立工件坐标系，则如图2所示；若以角度t为变量，则该空间曲线槽在XOY平面的方程是：

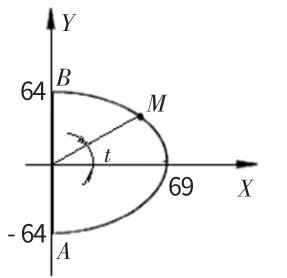
图2 XOY平面上的投影

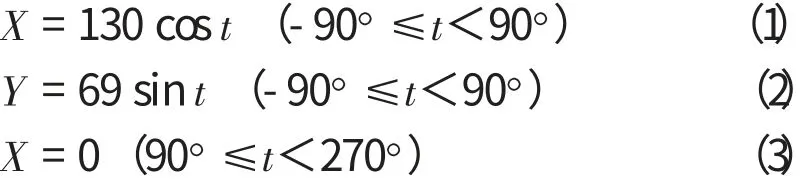
与此同时，该曲线槽随角度t展开时的Z坐标曲线如图3所示，与展开角度相对应的曲线方程可表达为：

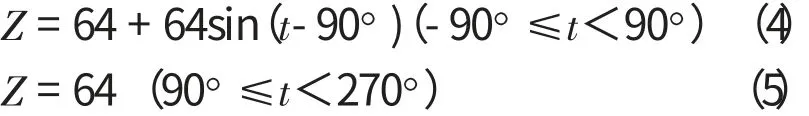
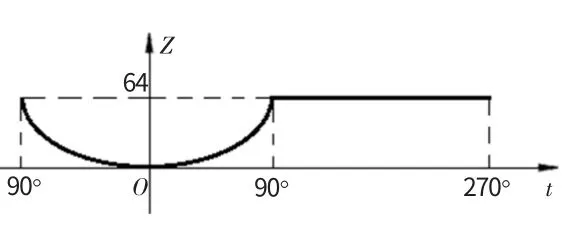
图3 随角度t展开的Z坐标曲线

2 刀具运动轨迹分析

用粗微分等步长逼近法加工曲线槽。数控系统一般只具有直线插补和圆弧插补功能，非圆曲线形状的工件一般运用逼近法来进行加工，其原理是根据零件图纸的轮廓形状误差允许值e允，通过计算确定逼近法加工的切削参数，如步进值或步进角度等，根据计算结果把曲线段划分为N段，再用N个小段直线来代替小段曲线。如果形状精度要求高，直线的段数就多。点与点之间的连接可以用G01直线插补指令来完成。

考虑编程取值的方便和曲线形状的因素，选择图1中A点作为切削起点，逆时针经M点、B点再回到A点。刀具每进一刀，重复上述路径一圈。曲线槽的端面是半圆形轮廓，如图4所示，半径为R=7 mm，可用球头刀粗精铣。如果不考虑刀具切深，则曲线槽上任意一点M的空间坐标（X，Y，Z）可以根据上述方程（1）~（5）计算得到。

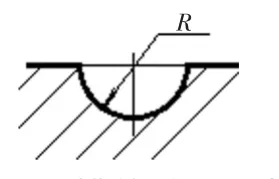
图4 槽的端面形状

3 宏程序的编写

3.1 变量的确定

以角度t 为第一自变量，取曲线槽上任意相邻两点间的角度⊿t相等，定义为步进角度。然后由参数方程分别计算出各点对应的X值、Y值和Z值，用G01进行空间直线插补，以空间直线来逼近空间曲线。

同时以进刀切深值为第二自变量，在每次进刀时Z坐标也跟着变化。

在编程时要理顺两个自变量之间的关系，利用宏程序的循环嵌套方式进行编程。

3.2 最小角度步进值⊿t的计算

（1）求曲线段的最小曲率半径Rmin

如图5所示为椭圆曲线，其曲线方程为：

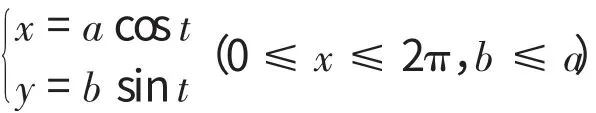
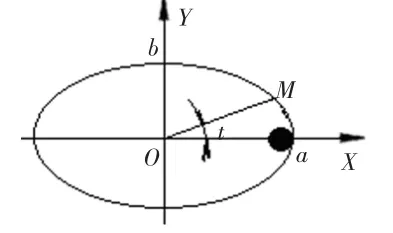
图5 椭圆曲线

根据椭圆的形状可判断，椭圆在（+a，0）和（-a，0）处曲率最大，即曲率半径最小，且根据椭圆曲率半径计算公式得：

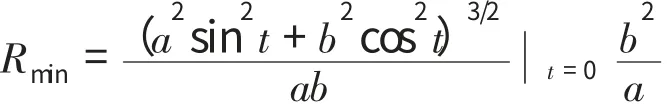
根据曲线槽的参数可知：

椭圆1：a=130，b=69

椭圆2：c=130，d=64

将其值分别代人上式计算得

椭圆1：R1min=692/130=36.623

椭圆2：R2min=642/130=31.508

（2）求插补步进角

将曲率半径最小处M点附近段轮廓放大，如图6所示，则在△O1MN中，有

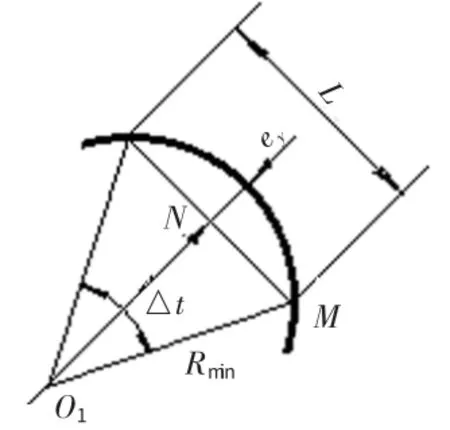
图6 步进角的计算图

经计算简化后得：

从△O1MN中还可得到：

将（6）式代入得：

Rmin取椭圆1和椭圆2中的最小值，即Rmin=R2min=31.508

如果曲线轮廓公差e=0.05，一般加工时其允许误差ey取其值的1/5-1/10，取上限1/5,得：ey=0.01。将Rmin=31.508和ey=0.01代人式（7），计算后得△t=0.204°。

即满足轮廓公差要求的步进角是0.204°。

3.3 宏程序

现选用FANUC 0i系统进行编程，由于篇幅有限，在这里只写出粗加工的程序。精加工时只要修改刀具切削进深值，调用子程序即可。

O 0001；（子程序名）

N10#1=130（椭圆1的长半轴为130）

N20#2=69（椭圆1的短半轴为69）

N30#3=130（椭圆2的长半轴为130）

N40#4=64（椭圆2的短半轴为64）

N50#101=64（当前铣刀Z位置）

N60#102=57(槽底Z坐标)

N70#103=-2（切深递进值）

N80 WHILE[#101 GE#102]DO1(刀具进深位置的条件判断)

N90#101=#101+#103；（递进切深）

N100 G01Z#101 F100;（开始切深进刀）

N110#10=-90（角度t的初始值为-90°）

N120 WHILE[#10 LE 90]DO2（角度条件判别）

N130#11=0.204（角度t的步进值为0.204°）

N140#10=#10+#11;（更新角度变量）

N150#12=#1*cos#10;(计算X坐标)

N160#13==#2*sin#10；(计算Y坐标)

N170#14=#101+#4+#4*sin(#10-90)(计算Z坐标)

N180 G01X#12Y#13Z#14;（空间直线切削）

N190 END 2;（结束循环2）

N200 G01X0Y-69;

N210 END 1;（结束循环1）

N220 M99;（子程序结束）

O1208：（主程序名）

N10 G54 G90G40 X0 Y0 Z15;（进入加工坐标系）

N20 G00 X0 Y-69;(快移至下刀位置A点)

N30 M03 S600 M08;（主轴转速600r/min，开冷却液）

N40 G0 Z66;（快速下刀接近A点上方）

N50 G01 Z64 F100;（工进至曲线A点）

N60 M98 P0001;（调用子程序O0001）

N70 G90 G01 Z66;（抬刀至工件上方）

N80 G0Z100;（快速抬刀至Z100处）

N90 M05M09;（主轴停，关冷却液）

N100 M30;（主程序结束）

4 结束语

宏程序是用户提高数控机床性能的一种特殊功能，是通过对变量赋值及变量之间的运算编制加工程序，具有灵活性强、通用性和智能性好等特点，非常适合非圆曲线或方程曲面类零件的加工编程。宏程序的程序段数量少，且简洁易懂，是CAD/CAM软件无法取代的原因之一，在类似凸轮零件的工件加工中巧用宏程序将起到事半功倍的效果。但宏程序的编制对编程人员的专业素质要求较高，编程人员除了要掌握宏程序的基本编程指令外，还要求能够建立零件走刀过程的数学模型和建立相应的数学关系表达式等，但这种编程方式可解决普通程序无法解决的难题。

[1]石永刚.凸轮机构设计与技术创新[M].北京：机械工业出版社，2008.

[2]杨静云.数控编程与加工[M].北京:高等教育出版社，2010.

[3]吴金会，刘 越，王祥祯.基于宏程序的方形体斜角面铣削加工应用研究[J].组合机床与自动化加工技术,2012（5）：94-96.

[4]胡运林.圆管体相贯坡口数控铣削加工技术的研究[J].组合机床与自动化加工技术，2012（2）：109-112．

[5]赵岐刚，于世忠.基于宏程序的圆柱凸轮数控加工[J].煤矿机械，2011（2）：117-118．

[6]颜明西，王斌武.宏程序在加工椭圆柱凸轮余弦曲线旋槽的应用[J].煤矿机械，2009（5）：110-111．