地震学百科知识（二）震源物理（下）＊

许忠淮 李世愚

（中国地震局地球物理研究所，北京100081）

地震科普

地震学百科知识（二）震源物理（下）＊

许忠淮 李世愚

（中国地震局地球物理研究所，北京100081）

7 震源参数（earthquake source parameters）

除上述震源机制参数或地震矩张量解的参数外，描述地震震源还经常使用一些其他的几何参数和物理参数。

7.1 标量地震矩（scalar seismic moment）

对于天然地震，标量地震矩指双力偶点源模型的一个力偶的力矩值［（1）式］，或地震矩张量解的双力偶成分的大小［（6）式的MDC值］。研究机构在发布天然地震的地震矩张量解时，常将标量地震矩简记为地震矩。

7.2 地震能量（earthquake energy）

一次地震所释放的总能量E，是断层附近的岩层通过断层错动所释放出来的原贮存在岩体内的弹性应变能。这些释放的应变能转化为岩石摩擦滑动产生的摩擦热Wf、岩石破裂和破碎需要的破裂能Eγ和辐射地震波的能量Es。

地震时震源向外辐射出去的地震波能量Es通常只是地震释放总能量E的一小部分，通常把Es和E通过地震效率η联系起来，表示成

有人估计η只是百分之几到百分之十几的量级。

分析地震波记录的观测结果，可得到地震辐射的地震波能量Es，古登堡和里克特（1956）发现，浅源地震的Es与震级MS有如下经验关系：

式中，Es以焦耳（J）为单位（1J＝107erg），MS是面波震级。出现数字地震记录后，有人［1］分析世界浅源地震数字地震记录的结果，得出上式最后的常数是4.4。

7.3 应力降（stress drop）

地震发生前后地震断层面上剪应力的变化。

地震的应力降有静态应力降（static stress drop）和动态应力降（dynamic stress drop）之分。前者指断层面上某一点的剪应力自破裂前至破裂后最终状态的变化值；后者指断层上任一点在滑动前的初始应力与滑动过程中该点的滑动摩擦应力之差。

令地震前断层面上的剪应力值为σ0，称为初始应力；若震后最终剪应力为σ1，则

称作地震的静态应力降，该量在整个断层面上的平均值是地震的平均应力降，即通常所发布的一个地震的应力降大小。

观测结果表明，构造地震的静态应力降基本在0.1～10MPa的范围内。由于地下岩层通常都受到一定的围压作用，一般认为，震后断层面上的剪应力不会降至零，大地震之后余震不断也说明震后剪应力不为零，因而地震的应力降Δσ大小并不能代表地震前震源区所受到的构造剪应力σ0的大小，Δσ只是σ0的一部分，地震只释放了构造应力的一部分。有些研究人员已注意到，根据地震波观测推断的板块内部地震的应力降要比板块边界地震的应力降高一些。

地震波的观测结果说明，地震断层的破裂总是从一个破裂点（或小破裂区）起始，然后快速扩展出去的。Yamashita［2］提出，断层面上任一点在其破裂过程中，该点的剪切应力实际有一个随时间变化的过程，如图11所示。动态应力降Δσd指地震断层上任一点在滑动前的初始应力σ0与滑动过程中该点的滑动摩擦应力σd之差，动态应力降可随断层面上的位置而变化。此外，断层的剪切破裂应力（即剪切破裂强度）σs与动摩擦应力σd之差称为有效应力σeff，这是对断层面上质点运动起加速作用的应力。

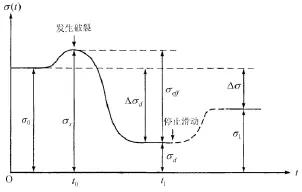
图11 断层面上任一点的剪应力自破裂前至破裂后随时间t的变化。σ0是初始应力，σs是断层介质的剪切破裂应力，σd是动摩擦应力，σ1是震后应力，Δσd是动态应力降［2］

7.4 震源时间函数（source time function）

描述地震发生时震源辐射地震波能力随时间变化过程的函数。

根据震源的弹性理论，双力偶点源在无边界的均匀介质中产生的P波位移场，用图12的坐标可表示为

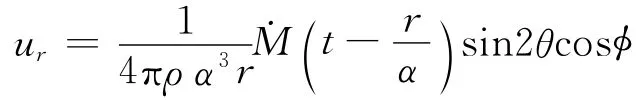
式中r是源点至接收点的距离，ρ是密度，α是P波传播速度，t是以震源断层开始错动时刻为零点的时间；因P波只有r方向的分量，所以位移用ur表示。式中M（t）是随时间变化的地震距，而.M（t）叫做地震矩率函数，它是控制震源地震波辐射的震源特性因子。常常将地震矩率函数的强度部分和随时间变化特征分开表述，即令

M0是标量地震矩，.g（t）即是震源时间函数，地震矩率函数是地震矩函数

的时间微商，M（t）通过介质的剪切刚度μ、断层的错动历史D（t）和发生位错的断层面积的变化A（t），描述了断层滑动的过程。

在一个地震的断层滑动过程完成后，地震的标量地震矩大小可用

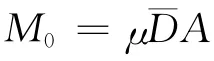
表示，ˉD是断层面积A上的平均滑动量，即平均位错。有人将M（t）写为

并将无量纲的S（t）也称作震源时间函数。

图12 表达双力偶点源P波位移场的坐标系

可见，在地震震源研究中，地震矩率函数中的.g（t）和无量纲的地震矩函数S（t）都叫做震源时间函数。

7.5 拐角频率（corner frequency）

地震破裂过程所产生的远场辐射波发生在有限的持续时间中，相应地，在频率域中，远场波动的位移谱的频带宽度是有限的，在高频段，振幅按角频率ω的某次方（即ω-ε）衰减，0＜ε＜3。通常把双对数坐标下震源振幅谱高频渐进趋势（包络线）和低频趋势（即零频水平）的交点称作拐角（corner），与拐角相应的频率称作拐角频率［4］。震源尺度愈大，震源辐射的初始体波脉冲的宽度愈大，其频谱的低频成分越丰富，拐角频率愈低。图13给出确定位移振幅谱拐角频率的一例。

图13 斯里兰卡PALK地震台宽频地震仪记到的2008年5月12日四川汶川8级地震的P波垂直向记录的位移振幅谱图，fc为拐角频率

作为震源参数之一的拐角频率，也可作如下理解。任何一个地震都有描述其震源变化过程的震源时间函数，该函数的傅里叶谱称为震源谱。震源位移振幅谱通常分为高频段和低频段，在用双对数坐标表示震源位移振幅谱时，可以分别用两条直线逼近高频段和低频段的变化趋势，两直线的交点对应的频率，也是低频段向高频段发生拐折的点对应的频率，即称为拐角频率。

7.6 视应力（apparent stress）

这是地震断层面上总应力的一部分，由于这部分应力的作用，地震产生了地震波的辐射。

记地震前断层面上的剪应力值为σ0，震后最终剪应力为σ1，则

可看成是断层面上的平均剪应力。若断层面积为A，断层平均错距为D，则可用断层面上的合力ˉσA使断层发生位移D所做的功来估计地震释放的总能量E：

地震向外辐射的地震波能量Es只是地震释放总能量E的一部分，即

η＜1，是地震效率。由上两式可得

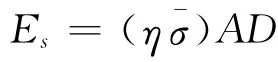
此式说明，地震辐射地震波的能量可看成是断层面上作用的等效平均应力

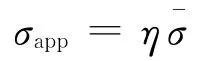
做功的结果，σapp就称作视应力。也可以说，视应力是从地震辐射的地震波能量大小看到的地震断层面上作用的平均应力。

通常不知道地震效率是多大，所以难以直接从平均应力来估算视应力大小。但由于地震的标量地震矩M0为

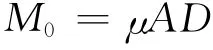
μ是岩石的剪切弹性模量，所以可用地震波辐射能量Es与地震矩M0的比值来估算视应力：

因为Es和M0都可由地震波观测估算出来。

7.7 断层长度（fault length）

地震断层最大破裂尺度的度量。地震产生的断层面的几何形状可能因地震的不同而不同，比如：较小的地震断层面可能近似为圆盘形或椭圆形，而浅源大地震的断层面一般可用矩形来近似。断层长度常指断层面的长边的长度，而短边的长度叫做断层宽度。

地壳上层是易发生岩石脆性破裂的脆性层，厚度一般是十几到二十几公里；而下层因温度较高易发生塑性形变，不易发生脆性破裂的地震。浅源大地震的岩层破裂可延伸百千米、甚至数百千米，破裂主要沿地壳上层的脆性层扩展，因而可用长的矩形断层来表示断层面的形状。

7.8 地震位错（earthquake dislocation）

天然地震的发生总是伴随着断层的错动或者断层两盘的相对运动。地震发生前位于断层面两侧上同一位置的点，在地震发生后不再位于同一位置，那么，这两个位置之间的差，就叫地震位错。

7.9 震源方向效应（source directivity）

指由于断层破裂沿特定方向快速传播引起的辐射地震波的振幅和频率与方向有关的现象。

一些断层面相对窄长的大地震，当破裂从断层一端向另一端快速扩展时（称单侧破裂），这就相当于有一个向特定方向移动的震动源，迎着破裂方向的观测点（图14中的正x方向）记录到的地震波，频率会变高，振幅会变大；而背着破裂方向的观测点（图14中的负x方向）记到的波，频率会变低一些，振幅会降低一些（图14）。这与观测到移动声波源显示出的多普勒效应的原理是一样的。

有时断层的破裂从中间某处开始，向两侧扩展，这时震源方向性效应表现为接近破裂方向的观测点记录到的波的频率和振幅会偏高一点，而与破裂传播方向接近垂直的方位上的观测点，记到的波动将与震源不移动情况下辐射的波动一样。大地震的震源方向效应常会加重地震在特定方向上引起的破坏程度。

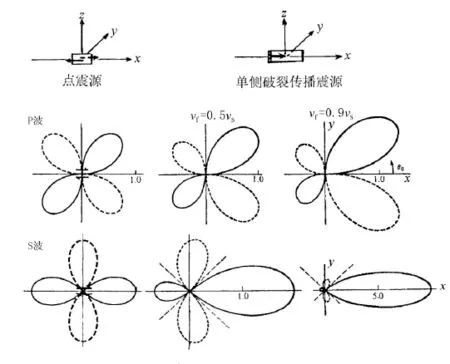
图14 断层破裂传播引起的地震波辐射花样的方向性效应。中、下图给出P波和S波在震源坐标（上图）的χ-y平面内用玫瑰瓣表示的辐射花样，原点至玫瑰线上任一点连线的长度代表该连线方向上波振幅的相对大小。实线对应挤压P波或沿逆时针方向位移的S波，虚线反之。vf是破裂扩展速度，vS是S波传播速度

7.10 地震破裂速度（seismic rupture velocity）

指地震断层破裂的扩展速度。根据对震源初始破裂点位置的测定和震源辐射地震波的方向效应的观测，推断出较大地震的破裂扩展速度大多在2～3km／s；有人已发现有少数大地震，断层破裂扩展速度可超过地壳内S波的传播速度，即超过约3.5km／s。地震断层破裂连续扩展的速度不会超过地壳的P波传播速度。

断层的剪切破裂有两种不同类型（图15）：一种是切平面剪切破裂（in-plane shear crack，材料断裂力学中称Ⅱ型裂纹），破裂的传播方向与断层的错动方向一致；另一种是法平面剪切破裂（anti-plane shear crack，Ⅲ型裂纹），破裂的传播方向与断层的错动方向垂直［4］。已有的理论研究结果认为，剪切破裂的传播速度与破裂类型有关。对切平面剪切破裂，取决于构造剪应力大小和断层摩擦滑动的具体条件，破裂传播速度可取低于瑞雷波速度的数值，或取高于剪切波速度（不超过纵波速度）的数值，但一般不会稳定地取介于瑞雷波速和剪切波速之间的数值。对法平面剪切破裂，破裂传播速度可取低于剪切波速度的任意数值，上限是剪切波速度。

图15 断层的两种剪切破裂方式

已有一些实验结果和观测结果支持以上的理论推断。例如2001年11月14日中国的昆仑山MS8.1大地震，使近东-西走向、近直立的昆仑山断层产生了一段约400km长的左旋走滑破裂，这是切平面型剪切破裂（图15左）。Bouchon和Vallee［3］根据区域地震台的宽频带地震波记录，推断出由西向东传播的破裂，以接近瑞雷波的速度破裂了开始的100km段，以后很快转为以超剪切波的速度（最高达5km／s）破裂了断层的其余300km。

8 断层滑动方式（fault slip type）

8.1 稳滑（stable slip）

断层两盘以稳定的常速度相对缓慢滑动，在这种滑动过程中断层面上的剪应力是准静态地下降的。

地壳内的许多断层会长时期（数十年、数百年甚至更长）处于稳滑状态，滑动速率可以为每年1毫米至几十毫米的量级。从长期看，断层稳定滑动的速度也可能有些变化，但多是很缓慢的变化。稳滑断层没有弹性波的辐射。断层稳定滑动的方式也称为断层的蠕动。有些大断层的某些段落是蠕动段，而另一些段落处于不滑动的闭锁状态，可称为断层的闭锁段。在周围构造应力的作用下，断层的闭锁段会逐渐积累应力，成为可能发生地震的地方。但目前实际确定断层的闭锁段是个复杂而困难的问题，即使确定了可能发生地震的闭锁段，更困难的问题是，一般情况下不能准确确定发生大地震的时间。

8.2 粘滑（stick-slip）

断层两盘的错动表现为较长时间的粘着（stick）和突然急速滑动（slip）重复交替出现的现象，称为断层的粘滑。

断层的粘滑以间隙性的急跳式滑动为特征，发生粘滑的条件与断层两侧的岩石性质、断层表面的摩擦特性和应力加载条件等有关。例如，含较厚断层泥的断层较易发生稳定滑动，不利于发生粘滑；对给定的岩性和断层面特性，增大断层面上的正压力可能使断层从稳滑状态转变为粘滑状态。

粘滑的概念原是在有预切面岩块的摩擦滑动实验的基础上提出的，1966年美国W.F.Brace和J.D.Byerlee［5］建议用岩石摩擦滑动出现粘滑来解释地震发生的机制。他们强调，地震并不是简单地因为岩石所受的应力作用超过岩石的强度而发生的破裂，而是由于断层面上的摩擦力随断层的滑动发生变化，使断层滑动失去稳定性而发生的。断层发生失稳滑动后，由于断层面上产生了应力降，也由于摩擦力随断层滑动发生了变化，可以使断层重新回到稳定的粘着状态，等待下一次粘滑的发生。而岩石破裂模型虽能解释破裂的起始，但不易解释破裂的停止；有时需人为地引入高强度的障碍区或低应力区，才能解释破裂停止。

8.3 岩石破裂准则（rock fracture criteria）

这是判断岩石达到破坏程度与否的应力指标，有时被用作地震断层发生破裂和滑动的条件。对于完整岩石来说，最常用的破裂准则是莫尔（Mohr）准则，它的线性简化形式叫做库仑准则。根据岩石破坏实验结果，有人提出作用在岩石中某个面上的阻止岩石破坏的剪切力τf为：

其中τ0称岩石的聚合强度（cohesion），也可看成是无正压力条件下岩石的抗剪切强度，μ为岩石的内摩擦系数，τ0和μ是与岩石种类有关的材料常数；σN是作用在所考虑的面上的正应力。库仑准则认为，当作用于岩石中某面上的实际剪切力τ满足条件

时，岩石就发生破裂。

9 震源模型（seismic source model）

9.1 地震成核（nucleation）模型

这是关于地震断层破裂起始过程的模型。地震成核模型有两种，第一种认为是岩体内的微破裂集结而形成了地震断层的宏观破裂，这称为广义成核模型；第二种认为是剪切滑动面上临界滑动段的形成而导致了地震破裂的起始，这称为狭义成核模型。

微破裂集结的学说最初来自断裂力学和损伤理论，用于解释金属和岩石介质内部裂纹的起始扩展，其内容是在原始宏观裂纹端部附近应力集中区域有许多微裂纹逐渐萌生、增长，这个区域叫做过程区。随着微破裂密度加大，相互作用逐渐增强，微破裂发育从无序向有序转变；当微破裂局部密度达到临界值时，过程区内的微破裂聚集，并与原始主裂纹贯通。根据分形理论，这种集结过程在尺度上是多层次的，而且是自相似的，因此微破裂的集结学说被推广到百米乃至千米级尺度，用于解释地震断层的形成与起始扩展过程。

狭义成核模型以断层面摩擦本构关系为理论基础，用状态变量描述断层摩擦滑动过程。其内容主要是：①存在一个临界尺度，在滑动段小于该尺度时，滑动是稳定的，扩展速度很慢，这个阶段要持续很长时间；②在滑动段扩展到大于临界尺度时，剪应力超过稳定状态的摩擦阻力，扩展加速，很快变成失稳滑动。该模型预示，在快速扩展的主破裂发生前的缓慢预滑可能产生长周期形变波。

9.2 凹凸体（asperity）模型

凹凸体的概念来自摩擦学，认为固体介质摩擦面上存在许多小的凸出部分，接触面的粘着部分和滑动部分交替分布，使得摩擦面上应力分布不均匀。后来有人将凹凸体概念推广用于千米级的地震断层面上，用来解释地震的多重事件，特别是大地震的多重性。这些人认为地震发生前，断层面上的凹凸体处于闭锁状态，从静摩擦变成滑动摩擦实际是这些互相啮合的凹凸体被解锁的过程。当介质为脆性时，这些凹凸体接连解锁表现为多重破裂。凹凸体的破裂就构成整个大破裂过程的一个个子事件。

9.3 障碍体（barrier）模型

认为地震断层面上的介质强度不均匀，地震时强度低的部分先破裂，强度较高的部分形成地震断层扩展的障碍体。地震断层在扩展时有可能被障碍体阻挡而暂时停止，或越过障碍体继续扩展，使地震破裂表现为多重事件。被越过的障碍体在以后仍然可能破裂，形成余震。

9.4 膨胀模型（dilatancy source model）

这是基于无预存切面岩样的岩石力学实验结果建立的试图解释地震的可能前兆的震源模型。该震源模型的主要实验依据是美国布雷斯（W.F.Brace）等人［6］1966年在美国地球物理研究杂志上发表的实验结果。该实验表明，岩石在破裂前出现体积膨胀现象。即使在高围压条件下，只要有差应力存在，这种现象就依然出现。布雷斯等用断裂力学的理论和实验解释了该现象的机理，认为是岩石内部的越来越多的微裂纹在差应力作用下出现许多拉张破裂所造成。膨胀模型有两种，一种由A.Nur和C.H.Scholz等人（1972—1973）提出［7］，认为在地震前，岩体膨胀使原来的孔隙饱和度降低，孔隙压力减少，从而使岩体的抗剪切能力提高，叫做岩石的硬化；而周围岩体的水逐渐向不饱和区域渗透，随着时间推移，膨胀区域的岩体水饱和度逐渐恢复，岩体的抗剪切能力下降，地震发生。该模型与水有关，因此也称作膨胀-扩散（dilatancy-difusion）模型，或湿模型。另一种模型认为，由孕震区的微裂纹扩展和集结也可以导致地震断层的破裂起始，从而引起地震发生。该模型由前苏联大地物理研究所提出，因此也叫做IPE（Institute Physics of the Earth）模式。该模型认为孕震过程可以没有水的参与，因此也叫做干模式。

这些基于均匀岩石样品实验结果提出的震源模型，能否用来解释天然地震（尤其是大地震）的震源过程，尚未有公认。

（作者电子信箱，许忠淮：xuzh＠cea-igp.ac.cn）

［1］Choy G L，Boatwright J L.Global patterns of readiated seismic energy and apparent stress.J.Geophys.Res.，1995，100（B9）：18205-18228

［2］Yamashita T.On the dynamical process of fault motion in the presence of friction and inhomogeneous initial stress：Part I，Rupture propagation.J.Phys.Earth，1976，24：417-444

［3］Bouchon M，Vallee M.Observation of long supershear rupture during the magnitude 8.1Kunlunshan earthquake.Science，2003，301（5634）：824-826

［4］安艺敬一，P G理查兹.定量地震学：理论和方法.北京：地震出版社，1987

［5］Brace W F，Byerlee J D.Stick slip as a mechanism for earthquakes.Science，1966，153：990-992

［6］Brace W F，Paulding Jr B W，Scholz C.Dilatancy in the fracture of crystalline rocks.J.Geophys.Res.，1966，71（16）：3939-3953.doi：10.1029／JZ071i016p03939

［7］Scholz C H.The Mechanics of Earthquakes and Faults（Second edition）.Cambridge：Cambridge University Press，2002

P315.3＋3；

A；

10.3969／j.issn.0235-4975.2013.03.008

2012-11-07。