基于标定板特征的摄像机线性标定方法研究
赵 群,杨进华
(长春理工大学 光电工程学院,长春 130022)
0 引言
机器视觉的一个主要目标是从摄像机获取的图像信息出发计算三维空间中物体的几何信息,并由此重建和识别物体。空间物体表面某点的三维几何位置与其在图像中对应点之间的关系由摄像机成像几何模型决定,摄像机标定就是确定这种几何模型参数的过程。几何模型参数包括内部参数和外部参数两类,摄像机内部参数是由摄像机内部几何和光学特性决定的,主要包括焦距f和主点坐标(u0,v0),还有镜头畸变的各类畸变系数等。摄像机外部参数是指摄像机坐标系相对世界坐标系的位姿关系,包括旋转矩阵R和平移向量t。
摄像机标定方法大致可分为两大类:传统摄像机标定法和摄像机自标定法。自标定法虽然不需要空间场景的三维几何信息,仅仅利用摄像机获取的图像中的信息就可以确定摄像机的内部参数,但是需要控制摄像机做严格运动,实验要求比较高,稳定性差。传统标定法典型算法有直接线性法[1]、非线性优化法[2]、Tsai两步法[3]、Zhang的平面法[4]等。其中直接线性法由于不考虑镜头畸变,精度较低;非线性优化算法比较繁琐,速度慢,且对初值选择依赖性较大,如选择不当,很难得到正确结果;Tsai两步法和Zhang的方法均先用线性法求出部分参数,而在考虑镜头畸变中也引入了非线性优化。本文提出一种考虑了镜头畸变的线性标定法,避免了非线性优化,对主点坐标、纵横比、有效焦距、一阶径向畸变系数等5个内部参数以及旋转矩阵和平移向量的6个外部参数进行了标定。实验证明本文提出的算法精度较高。
1 摄像机模型
空间任何一点P在图像上的成像位置可以用针孔模型近似表示,即点P在图像上的投影位置为光心Oc与P点连线OcP与图像平面的交点Pu,这是理想的透视投影模型。在实际中由于摄像机镜头光学系统的加工误差和装配误差,摄像机像面上的实际成像与理想成像之间存在光学畸变误差。主要畸变有径向畸变、偏心畸变和薄棱镜畸变,在工业视觉中一般只需要对径向畸变进行校正,Tsai[3]指出,在对摄像机进行标定的时如果考虑过多的非线性畸变会引入过多的非线性参数,不仅不能提高标定精度,反而会引起解的不稳定。因此我们采用一阶径向畸变的针孔模型。
如图1所示该模型有四个坐标系:计算机图像坐标系Ouv;图像坐标系oxy;摄像机坐标系ocxcyczc;世界坐标系OwXwYwZw。
从世界坐标系到计算机图像坐标系的变换分为如下4步[5]:

图1 一阶径向畸变针孔模型
(1)世界坐标系与摄像机坐标系的变换,可以用旋转矩阵R和平移向量t来描述:

(2)摄像机坐标系到理想图像坐标系的变换:

(3)理想图像坐标系与实际图像坐标系的转换,考虑一阶径向畸变,建立畸变模型:

式中,r2d=x2d+y2d,k1为一阶径向畸变系数。
(4)实际图像坐标系到计算机图像坐标系的转换:
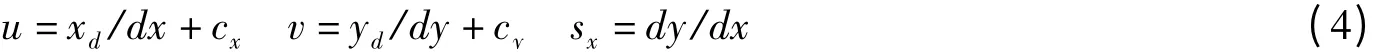
式中,(cx,cy)为主点坐标,(dx,dy)分别为图像平面上x,y方向上单位像素间的距离,sx为图像纵横比。
2 基于SIFT算法求解HALCON定标板特征点的图像坐标
本文采用MVTec公司的HALCON提供的标准标定模板(7×7),尺寸0.3m×0.3m,边框内圆点的中心距为0.0375m,精度高达微米级。如图2所示:

图2 HALCON标定板
SIFT(the Scale Invariant Feature Transform)算法[6,7]是David G.Lowe提出的一种基于尺度空间、对图像放缩、旋转甚至仿射变换保持不变性的特征点提取算法。首先求出标定板图像的高斯尺度空间,通过变换不同的空间尺度因子,进行多尺度空间的极值点检测,即可较稳定获得标定板边框内各个特征中心点的亚像素坐标。实验所得图3如下:
如图3(b)所示,十字亮线代表已经获取到的特征点的中心坐标。在拍摄时,最好保证标定板和平台垂直且正对相机镜头,使得标定板上的特征点在摄像机坐标系下的z坐标值相同,以确保标定工作的顺利进行。

图3 标定板原图及特征点中心坐标提取
3 摄像机内外部参数的线性求解
3.1 标定图像主点坐标
本文采用直接光学法[8-9]。标定原理如图4所示:
激光光束射向镜头表面,大部分光透过镜头,部分光由镜头各表面反射。当激光光束与镜头不同轴时,在激光束出射光阑面上可观察到由反射光束形成的多个不同位置的弥散斑。此时调整激光束相对镜头的位置,当所有弥散斑刚好和出射光阑小孔重合时,认为激光束与镜头光轴重合。然后在镜头前的光轴上放一定倍率的衰减片,打开CCD相机,激光束在CCD像面上的像点即为镜头光学成像中心。通过求光斑图像的质心坐标,便为主点坐标(u0,v0)。
3.2 标定纵横比
由于摄像机焦距同时在x和y方向上缩放图像,所以垂直拍摄一个圆环,然后计算其在水平方向和垂直方向上的像素直径比即为纵横比sx。
3.3 求解旋转矩阵R和平移分量tx、ty

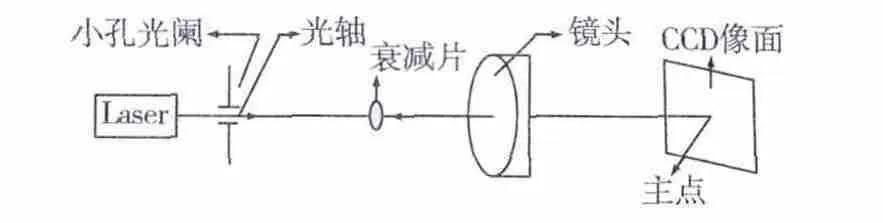
图4 直接光学法

3.4 求解焦距f、一阶径向畸变系数k1和平移分量tz
由公式(1)(2)(3)联合得:
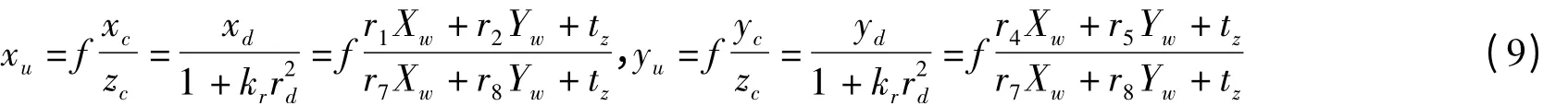
同样整理成含有f、k1和tz的线性方程:

式中,E=r1Xw+r2Yw+tz,F=r4Xw+r5Yw+tz,G=r7Xw+r8Yw,k=fk1
最后将(10)式中的两个方程合成一个线性方程组,用最小二乘法求解f、k1和tz三个参数的值。
4 实验结果及分析
实验采用分辨率为13001024pixel、像元大小4.65μm的OK-AC1300型号相机,工作输出8bitRGB图像,镜头为35mm定焦镜头。实际采集HALCON标定板图像大小为800600pixel,其特征点总数为49个,如图(3)所示。通过计算其图像坐标和世界坐标,按3节步骤进行标定,出现了随着测试点个数的变化焦距f不稳定的现象,如下图5所示:

图5 焦距f变化曲线
经过多次实验,焦距的变化很大程度上受平移分量tz的影响,由于参加计算的测试点的个数不同使得tz也随着变化,从而导致的焦距f不稳定。因此实验采用激光相位测距仪测量CCD像面到标定板的垂直距离,即tz。并对原算法提出改进,将(9)式修改为:

重新计算后得到焦距随着测试点的变化在f=35mm附近得到较好的收敛。如图6所示:

图6 标定t z(红线)与未标定t z(蓝线)的焦距f变化曲线
本文采用测试点的真实图像坐标与再投影后相应的图像坐标之差的模平均值来描述[10],单位pixel,公式如下:

其中(ui,vi)为测试点的真实图像坐标,(ui',vi')为再投影后的图像坐标,n为测试点数。
利用本文算法得到标定结果,如表1所示。

表1 摄像机线性标定数据
实验选择30个特征点作为标定点,其余19个作为测试点。进行误差分析后得EAVG=0.8376pixel,可见本文标定精度较高,从焦距的标定值和所用镜头焦距的设计值对比,也可得到验证。
5 结语
本文提出一种简单有效的摄像机线性标定法。选用高精度的HALCON标定板作为标定模板,用需要标定的CCD摄像机对其进行一次性拍摄,并应用SIFT算法提取标定板图像的有效特征点坐标,达到了亚像素精度。最后分步完成了摄像机的全部参数线性标定,避免了非线性优化的繁琐。标定过程中,由于受标定结果tz变化的影响,导致结果中焦距f等一些参数不稳定,因此本文对原算法进行了改进,将tz独立出来进行标定,从而使标定结果中焦距f获得较好的收敛性。实验表明本文标定精度较高,适合大多数摄像机标定,在机器视觉领域有广泛的应用价值。
[1]Y I Abdel-Aziz,H M Karara.Direct linear transformation from comparator coordinates into object space coordinates in close-range photogrammetry[C].In:Proceedings of the ASP Symposium on Close-Range Photogrammetry,Urbana,Illinois,1971:1-18.
[2]吴福朝,阮宗才,胡占义.非线性模型下的摄像机自标定[J].计算机学报,2002,25(3):276-283.
[3]Roger Y.TSAI.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV camera and lenses[J].IEEE Journal of Robotics and Automation,1987,3(4):323-334.
[4]Zheng-you ZHANG.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2000,22(11):1330-1334.
[5]徐杰.机器视觉中摄像机标定Tsai两步法的分析与改进[J].计算机工程与科学,2010,32(4):45-48,58.
[6]Lowe,D.G.Object Recognition from Local Scale-Invariant Features[C].In Process of the International Conference on Computer Vision,Corfu,Greece,1999:1150-1157.
[7]Lowe,D.G.Distinctive image features from scale-invariant key-points[J].International Journal of Computer Vision,2004,60(2):91-110.
[8]Lenz Reimar K,Tsai Ronger Y.Techniques for calibration of the scale factor and image center for high accuracy 3D machine vision metrology[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1988,10(5):713-720.
[9]王峰,周仁魁,杨小许,等.CCD摄像机图像中心两种标定方法的应用研究[J].光子学报,2006,35(2):294-298.
[10]张颖.一种摄像机亚象素线性标定方法[J].计算机工程与应用,2007,43(9):56-58.

