车牌倾斜校正算法研究及改进

陈 玲，李熙莹，卢 林

(1.中山大学物理科学与工程技术学院，广东 广州 510275; 2.中山大学工学院，广东 广州 510275;3.广东省智能交通系统重点实验室，广东 广州 510275; 4.视频图像智能分析与应用技术公安部重点实验室，广东 广州 510275)

0 引 言

随着智能交通行业的快速发展，开发各种自动化卡口系统成为迫切需要，车牌自动识别系统作为智能卡口系统的一个重要组成部分，成为当前研究的热点之一。车牌自动识别系统依次由定位模块、校正模块、分割模块和识别模块构成。定位模块在整个图像区域内实现车牌区域的定位;校正模块主要实现车牌区域的倾斜校正和灰度校正;分割模块将车牌区域的单个字符分割出来;识别模块实现车牌的颜色识别和字符识别。车牌倾斜校正是校正模块的一个关键技术。

由于摄像机与车牌平面存在一定角度，所以拍摄得到的图像上车牌区域相对于原来车牌平面存在一个3D 旋转角，近似地将这个3D 旋转分解为水平旋转倾斜和竖直错切倾斜。然后，分别对水平旋转倾斜和竖直错切进行校正。

目前已经研究出的水平校正方法主要分为3 类:

(1)直线检测法。检测出通过车牌区域内最多点的一条直线，根据这条直线的倾斜角校正水平旋转倾斜。主要算法有:Hough 变换法和旋转投影法。Hough 变换法，如文献［1-4］，这种方法对于车牌存在边框时检测效果较好，但是在不存在边框或者噪声影响严重的情况下，校正效果不理想。主要由于Hough变换本身存在缺陷:首先，旋转角度取的是一系列离散值，其精度受累加器步长的限制，步长取很小时，又会限制计算速度;其次，存在峰值扩散效应，对累加器进行投票时可能会投票到峰值附近的点;第三，容易产生局部极大值。旋转投影法，如文献［5-8］采用的Radon 变换就是一种旋转投影变换。对二值化或是边缘检测后的图像进行旋转投影变换，寻找变换后的极值点对应角度作为倾斜角。这种方法存在和Hough 变换同样的缺点。图像中的噪声点对于这两种方法有直接影响。文献［6］提出采用形态学边缘能够更好地抑制噪声且检测出稳定的边缘信息，校正效果更理想。文献［3］提出了Hough 变换和Radon变换结合的方法，应用Hough 变换检测水平倾斜角，然后运用Radon 变换检测竖直错切角。

(2)特征直线法。文献［9-17］提出了利用特征直线对车牌倾斜进行校正。文献［10］对车牌图像的Sobel 竖直边缘运用K-L 变换理论寻找一条特征直线，使车牌竖直边缘点到特征直线的距离的平方和最小，直线的倾斜角就是车牌的水平倾斜角，其实质就是按照图像点到直线距离平方和最小原则将图像区域的点拟合成一条直线。文献［11］根据图像几何矩理论，将图像本原坐标系的x 轴作为特征直线，利用坐标轴旋转角校正水平倾斜，与文献［10］计算出的水平倾斜角相同，只是建立在不同的理论基础上而已。文献［13］提出采用小波变换提取边缘，运用主成分分析法寻找一条特征直线。文献［15］采用KMeans 聚类的方法将图像像素分为两类，然后拟合出一条直线，利用直线斜率进行倾斜校正。文献［17］采用SOM 神经网络将图像像素分为两类，然后拟合出一条直线，利用直线斜率进行倾斜校正。这些直线也可称为特征直线，也可以归于特征直线法。文献［16］采用加权最小二乘法将图像区域拟合成一条直线，采用直线倾斜角校正水平倾斜。简而言之，特征直线法就是将图像区域内全部点或采用特殊分类法得到的部分点拟合一条直线，利用直线倾斜角校正图像倾斜。

(3)方向图像法。文献［18-19］提出了一种基于方向场倾斜校正方法，求出图像中每一点的方向，统计得到方向直方图，找出分布最多的角度，求出车牌倾斜角。

目前的竖直校正的方法主要有两种:(1)直线拟合法。拟合出平行四边形错切边直线方程，根据直线倾斜角校正错切，文献［11-12］提出采用相关系数校正法和最小二乘法拟合直线。(2)旋转投影法，文献［3］提出一种旋转投影的寻找错切角的方法。

本文针对直线投影法的缺点提出两种改进算法;根据特征直线原理讨论特征直线法的校正误差;推导一种有效计算方向图像的方法，使方向图像法鲁棒性更强。通过实验研究对比各种改进方法的校正效果;对于竖直倾斜，设计实验比较现有方法的校正效果。

1 水平旋转校正算法及改进

由于摄像头安装位置和镜头光轴方向的影响，投影在图像平面的图像是投影变换图像，车牌区域经过投影变换后近似为存在旋转的平行四边形，如图1所示。对于这样的变形分步骤进行校正，首先进行水平旋转校正，检测出水平旋转角度，通过旋转图像进行校正;对于竖直方向的错切形变，检测出错切角，运用仿射变换进行错切校正。

目前水平旋转校正方法主要有3 类:直线检测法、特征直线法、方向图像法。

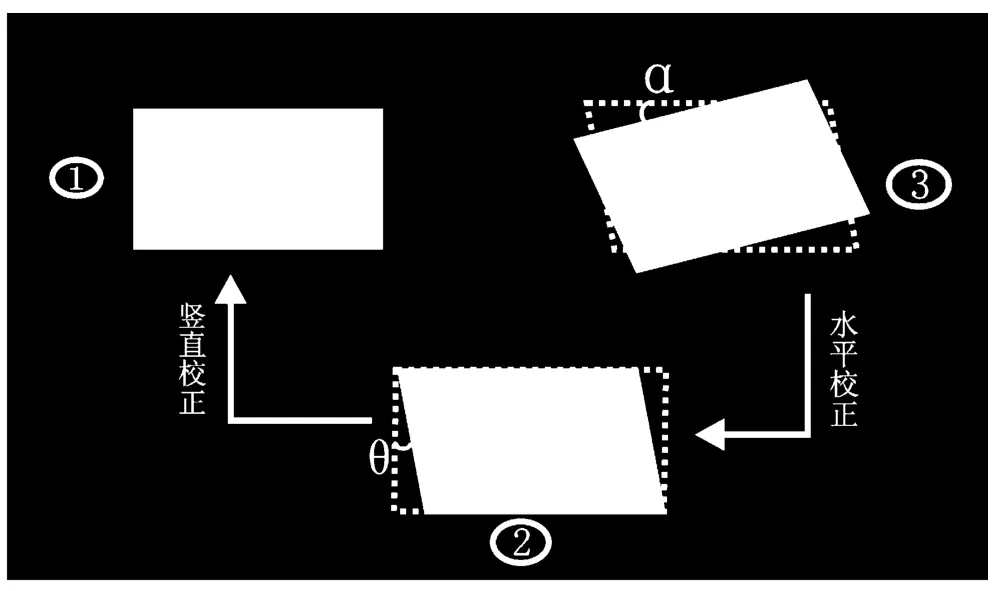
图1 车牌倾斜校正流程

1.1 直线检测法

直线检测的主要算法有Hough 变换和Radon 变换。首先对图像进行预处理，得到二值图或边缘图像，然后进行极值检测，利用极值所对应的角度计算倾斜角。实验部分结果可以看出边缘图的结果优于二值图，这主要是由于二值图引入的噪声较多。

Hough 变换本身存在伪极值、精度和峰值扩散3个缺点，使直接采用Hough 变换校正水平倾斜的效果不理想。Radon 变换检测法比较符合直观理解，但是和Hough 变换相似，同样也存在伪极值、精度和峰值扩散问题。

(1)伪极值。

Hough 变换中图像空间一条直线映射到参数空间为一个点，图像空间一个点映射到参数空间为一条正弦曲线，Hough 变换就是统计参数空间中的一个点有多少条正弦曲线相交，Hough 变换存在局部极值，使用极值抑制搜索算法可能得到一个伪极值。Radon变换同样也可能因为极值搜索而出现伪极值。

(2)累计步长影响计算精度和速度。

为了精确检测倾斜角度，累计步长不应该太大，但是过小的步长值又会大大降低计算速度。这是Hough 变换和Radon 变换的共同问题。

(3)峰值扩散效应影响。

峰值扩散效应是Hough 变换的一个普遍问题，一条直线上的点可能投影到参数空间相邻的几个点内，这就是峰值扩散效应。Radon 变换投影时也可能因为投影到变换域相邻的点而产生峰值扩散。

通过以上误差原因分析，提出两种分别针对Hough 变换和Radon 变换的改进算法。

(1)Hough 变换法改进。

①对预处理后图片选取参数空间累计角度步长Δθ 和长度步长Δρ进行Hough 变换，得到变换结果H，H的同一列具有相同角度参数，范围是［-90°，90°)，0°表示竖直方向，-90°表示水平方向。

②设定阈值T，将H中小于T(例如，选取H中最大值乘以0.6)的元素置为零。

③对②中得到矩阵的列进行累计求和，得到角度参数的频数分布h。

④车牌水平倾斜角在［-45°，45°］内，所以，分别统计(-90°，-45°］和［45°，90°)内的频数总和S1、S2。

⑤如果S1＞S2，则寻找h中(-90°，-45°］内最大值对应的角度θ0计算倾斜角，如果S1＜S2，寻找h中［45°，90°)内最大值对应的角度θ0计算倾斜角。如果S1=S2，采用θ0=90°计算倾斜角(此时倾斜角为0°)，选出角度θ0的区间称为角度选取区间。

⑥精度校正:由于Hough 变换累计步长影响校正精度，所以必须进行精度校正。⑤中得到的角度θ0和相应的选取区间((-90°，-45°］或［45°，90°))，计算h 在选取区间中θ0左右两边累计值s1、s2，采用式(1)计算校正值。

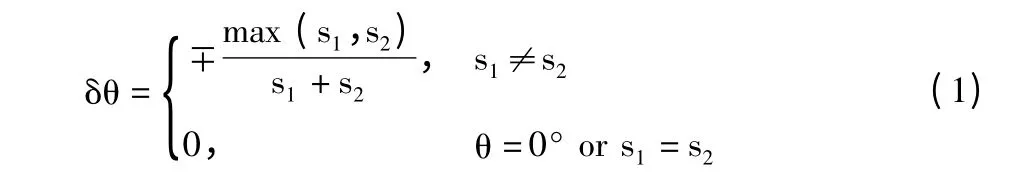
其中，s1＞s2取“-”，否则为“+”。

(2)Radon 变换法改进。

①由于车牌水平倾斜角在［-45°，45°］范围内，Radon 变换90°表示水平投影，Radon 变换角度取［45°，135°］，步长取Δφ，对预处理后车牌图像进行Radon 变换得到变换结果R。

②设定阈值T，将R中小于T(如选取R中最大值乘以0.8)的元素置为零。

③对②中得到矩阵按列进行累计求和得到角度参数的频数分布r。

④找出r中的最大值对应的角度φ，统计r 在φ左右偏移3°范围内的总和s1、s2，同样按Hough 变换精度校正方法，计算φ的校正值。

1.2 特征直线法(本原坐标轴法)

参与计算特征直线的图像像素点可以是经过分类法提取的部分像素点，也可以是图像区域内全部像素点，下面介绍的是未经过分类处理的特征直线法。

(1)原理。

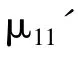
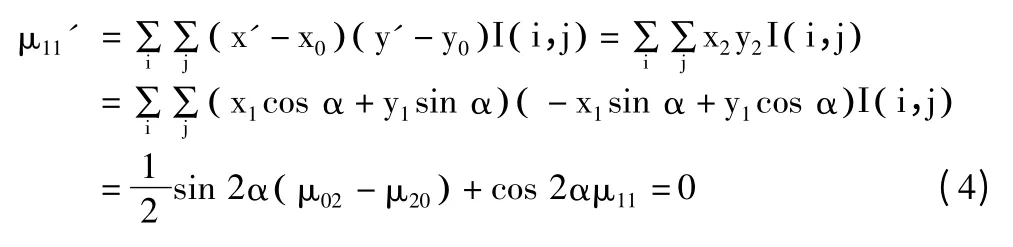
I (i， j) 表示图像像素灰度值，由(4)式推出:

μ11、μ20、μ02为坐标旋转前图像的中心矩。

(2)误差分析。

特征直线法在错切角不是很大时效果很好，但错切角很大时，检测结果存在偏差。水平矩形的特征直线倾斜角α=0，此时矩形特征直线为一条过矩形中心的水平直线，与平行四边形宽边平行。当矩形发生旋转倾斜以后，计算特征直线倾斜角，这个倾斜角就是旋转角，将特征直线旋转至水平可以校正倾斜。当矩形发生错切变成平行四边形(宽沿水平方向)，此时特征直线倾斜角不等于0，即特征直线不与宽边平行。平行四边形发生旋转倾斜时，将特征直线旋转至水平，并不能使平行四边形的宽处于水平方向，所以不能校正倾斜，如图2所示。

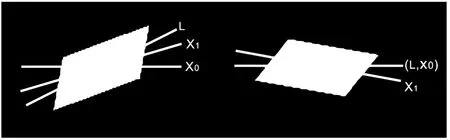
图2 存在错切的校正结果

如图3所示，x0为图像坐标系x 轴方向，x1为平行四边形宽的方向，L为特征直线。平行四边形的特征直线偏向较长对角线，特征直线法计算得到的倾斜角为α0(由x0轴正方向逆时针旋转得到时为正)，但是可以看出准确旋转角应为α，此时校正误差为α1(α1为锐角且由x1轴正方向逆时针旋转得到时为正，图3中为负)，α1为平行四边形水平时候特征直线的倾斜角。因此图3中会发生校正不足情况，而图2 则是校正过度。

图3 特征直线水平校正

图4 显示了采用不同错切角对水平矩形进行错切变换后得到的平行四边形特征直线倾斜角的变化，此时特征直线的倾斜角就是采用这种方法校正水平倾斜的误差。

对相同错切角，宽高比增大(宽指平行四边形较长边)，特征直线倾斜角绝对值变小，校正误差变小。对于固定宽高比，随着错切角的增加，倾斜角先增大后减小，错切方向影响倾斜角正负。

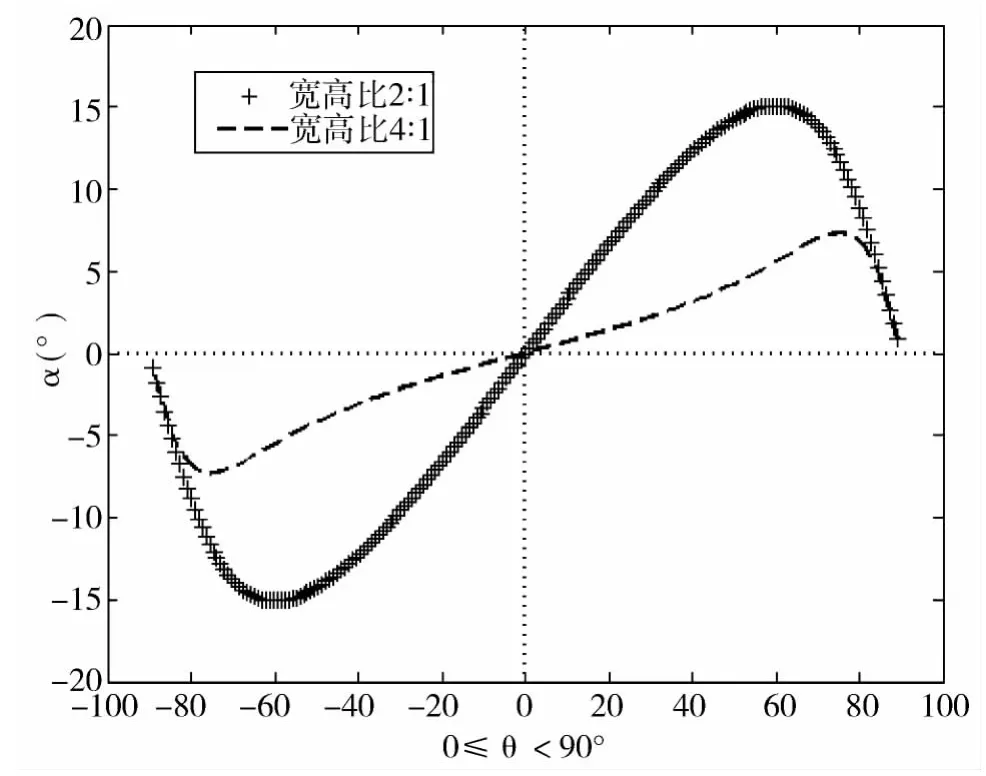
图4 不同错切角对应特征直线倾斜角

1.3 方向图像法

计算图像中各点的延伸方向，得到的方向矩阵可以表示成一幅图像，称为方向图像。对方向图进行统计，占比例最大的方向即为图像倾斜方向。根据式(6)计算图像中像素的方向角(此时定义为边缘切线与水平方向夹角)。

其中Ix、Iy是分别采用式(7)中的梯度模板Tx和Ty计算出的梯度图像。

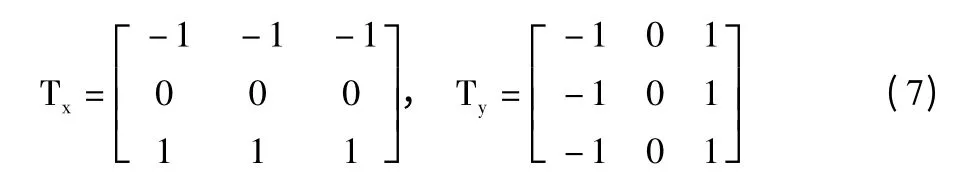
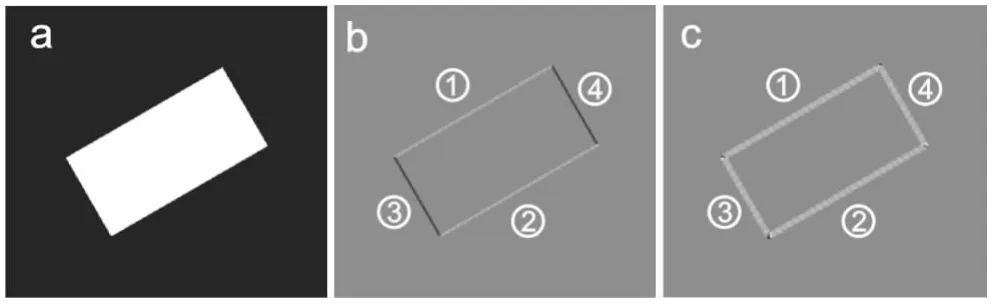
图5 矩形的方向图像

如图5所示为逆时针旋转30°后的矩形a的方向图，直接按式(6)计算方向时两条宽的边缘的梯度方向为30°(b中较亮的①和②两条直线)，其垂直方向的梯度为-60°(b中较暗的③和④两条直线)。但是，倾斜校正时，①和②偏离水平方向的角度和③和④偏离竖直方向的角度是相同的，如果互相垂直的两个方向计算结果相同，统计结果鲁棒性会更强。利用式(8)计算方向图像，得到的①、②、③、④四条边缘的方向角都是30°。旋转-30°(顺时针旋转30°)就能将矩形校正回来。

除了式(8)计算方向能使关系如①、②、③、④的四条边缘得到相同的计算结果以外，还有其他计算方法，通常这些计算方法都是利用反三角函数计算的。以下给出其他计算式的推导方法。首先水平倾斜由(-90°，90°)之间的角度表示。所以三角函数一个周期应该在(-90°，90°)内，且关于原点中心对称，满足条件的三角函数只有正弦函数sin kα 和正切函数tan kα(为方便推导与tan α的关系，取k∈ℝN+)。如果α 表示锐角，β=α -90°表示其垂直方向倾斜角，可以看出β∈ (-90°，0°) 。满足式(9)的正弦函数sin kα 和正切函数tan kα 即可作为方向计算式。

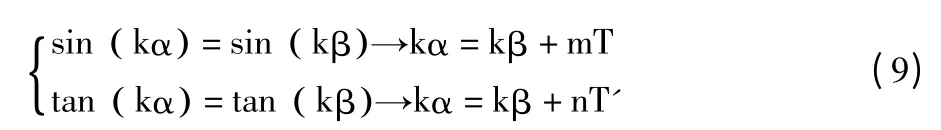
其中m、n都是整数，T 和T'分别为sin kα 和tan kα的周期:

结合式(9)和式(10)可以得到:

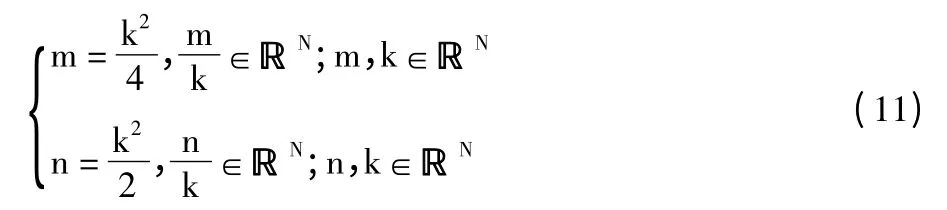
满足条件的三角函数是:

式(8)就是用tan 2α 和tan α的关系推导出来的，式(13)是利用sin 4α 得到的方向角计算式。

式(8)取值范围是［-45°，45°］，式(13)的取值范围是［-22.5°，22.5°］，都只能校正取值范围内的倾斜。利用式(8)计算时，如果倾斜角超出取值范围，则会被认为校正竖直倾斜，如图6所示，a1是水平倾斜30°的矩形，b1是利用式(8)计算得到的方向图像，边缘方向都是30°(逆时针偏离水平方向30°)，c1是校正结果。a2是水平倾斜60°的矩形，b2是它的方向图像，边缘方向都是-30°(顺时针偏离竖直方向30°)，c2是校正结果。式(13)只能校正［-22.5° ，22.5°］范围内的水平倾斜，图7是利用式(13)计算方向图像并校正20°倾斜的结果。

图6 tan 2α方向图像法倾斜校正

图7 sin 4α方向图像法倾斜校正

由于反正弦的定义域必须在［-1，1］之间，但是利用梯度求出的值不一定在这个范围内，所以反正弦的结果可能出现复数，此时，只能取它的实部进行计算。而tan 2α 则不受限制，所以一般方向图像法使用tan 2α 变换法进行校正。方向图像法思想虽然比较直观，但是受噪声影响严重，噪声过多则影响最后统计结果，从而影响校正结果。

为了减小误差。分别对计算式的分子和分母在像素的邻域模板内求和，计算得到的值就是中心像素点的方向值。图8 显示的是常利用的5×5方形模板和7×7圆形模板。

图8 5×5方形模板和7×7圆形模板

2 竖直错切校正

校正竖直错切的方法主要有错切边直线拟合法和基于预分割的旋转投影法。

2.1 直线拟合法

拟合出车牌边界所在直线，就可以根据直线斜率求出错切角，然后进行校正。

图9 错切校正

如图9所示，首先，统计车牌图像目标区域每一行最靠左的点坐标 (xi，yi)，组成一组点(p1，p2，…，pn)。其次，去除噪声过大的点。搜索得到的边界点中存在严重偏离车牌边框的误差点，这些误差点严重影响拟合结果，所以要去除这些噪声点的影响。误差点定义为不满足式(15)的点，即点的x坐标与坐标均值mx绝对差值超过标准差Sx的点，认为是应该去除的误差点。最后，将符合要求的边界点拟合直线得到直线倾斜角，计算图像错切角进行错切校正。

直线拟合法校正竖直错切虽然容易理解，但是应用于实际时误差相当大。原因主要有3 点，(1)一般车牌的左右边界不一定切割出来，这样提取的边界点就不准确，拟合出的直线误差很大。用于竖直校正效果不理想。(2)这种方法受图像中噪声点影响很大，拟合结果鲁棒性不强。(3)车牌图像尺寸一般不是很大，能够用于拟合直线的数据点很少，拟合结果稳定性较差。

2.2 旋转投影法

采用结合Radon 变换的旋转投影方法能提供更稳定的校正方法。如图10 对车牌二值化图像进行Radon 变换，变换以后投影区域内值为零数目最多的角度即为错切角(图像坐标系中沿-x方向错切时，错切角为负，反之为正)。这种方法是基于字符预分割提出的，校正结果更有利于后面的字符分割。车牌竖直错切角一般在［-15°，15°］，所以Radon 变换角度范围可以选取［-15°，15°］。

图10 Radon 投影校正

3 实验分析

3.1 水平校正

采用一套(220 张)由卡口系统实际拍摄得到，经过车牌识别系统定位与切割得到的车牌图像进行水平倾斜校正测试。首先采用顶帽变换对图像进行预处理，去除光照不均影响，然后利用顶帽变换后灰度图得到二值图和边缘图作为测试图片。将测试结果分为正确、未校正、错误3个级别。正确表示校正基本正确;未校正表示校正前后基本没有变化;错误为明显校正错误。测试采用数值观察+图像观察的方法。数值观察:观察倾斜角是否明显偏离根据摄像机位置事先得出的估算角(测试车牌约为3°);图像观察:人眼直接观察图像校正结果，判断测试结果类别。

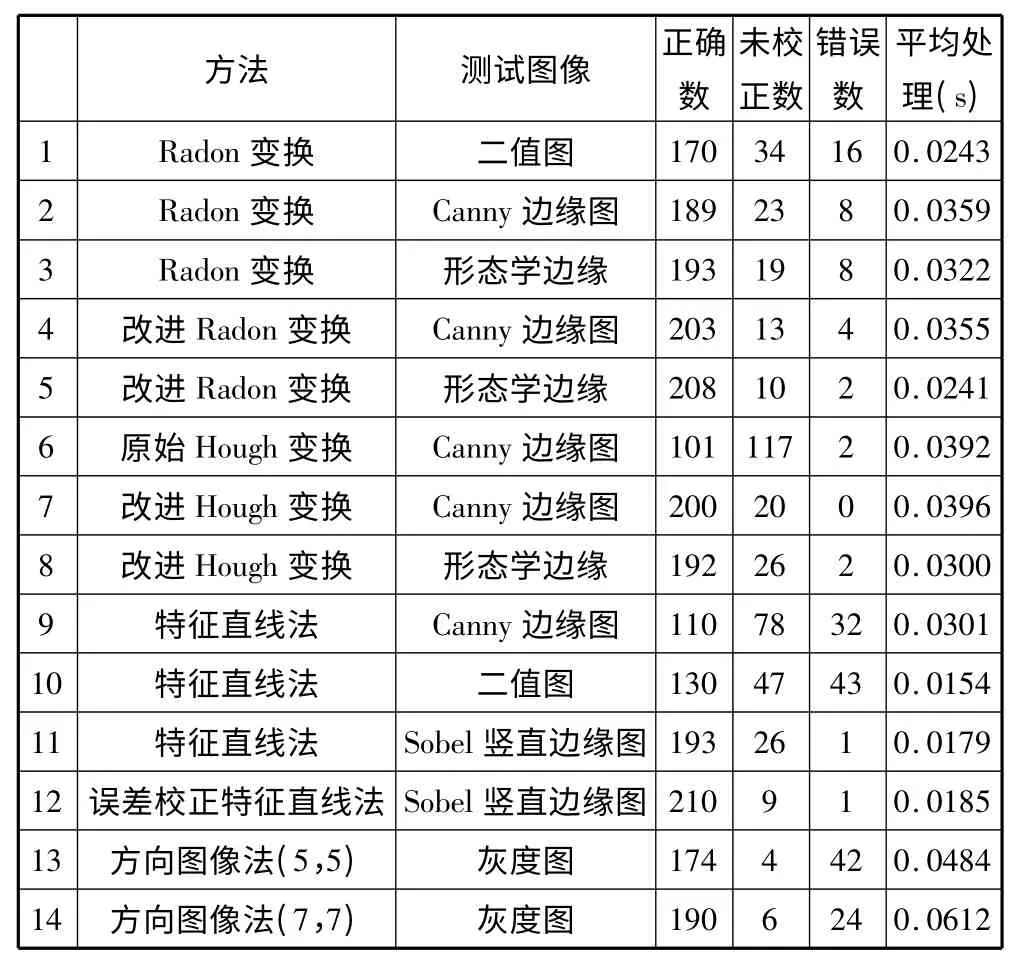
表1 水平校正测试结果

由表1中数据可以看出，Radon 变换法应用边缘图像要比应用二值图要好;原始Hough 变换正确校正率不是很高，改进后的Hough 变换校正效果较好;特征直线法结合Sobel 竖直边缘图能得到很好结果，并且计算速度较快，但是观察可知，特征直线法对于测试的这套车牌都存在校正不足的缺点，误差原因已在前面分析。根据车牌图像宽高比约3:1，估计错切角约2°，估计此时校正误差约为0.2°，所以实验12中采用0.2°误差进行误差校正，部分改善校正结果;方向图像法校正效果也较好，但是平均处理时间较长，实验中车牌图像平均尺寸为120×45，使用7×7圆形模板效果较好。综合正确率和速度进行考虑，方法5、7、12 明显优于其他方法，方法12中需要事先估计误差校正角，对于摄像机固定的系统才有效。同时实验数据可以看出各种改进算法都在一定程度上改进了校正结果。

3.2 竖直校正

对于竖直校正，由于实际拍摄得到的车牌错切角都较小，测试实验选用平拍得到的水平车牌图像进行人工错切变换。测试集选取了13 张实际拍摄的水平车牌图像，每一张图像在［-10°，-10°］内每隔2°进行一次错切变换，得到130 张测试图片，尺寸平均约为80×240。对这130 张测试图片进行错切校正。错切校正之前首先对车牌字符区域的上下边界进行精细定位，然后计算找出错切角，应用双线性插值法进行错切校正，如图11所示。表2 给出了130 张图片的测试结果。由实验数据可以看出旋转投影方法远优于直线拟合法。

图11 竖直错切校正

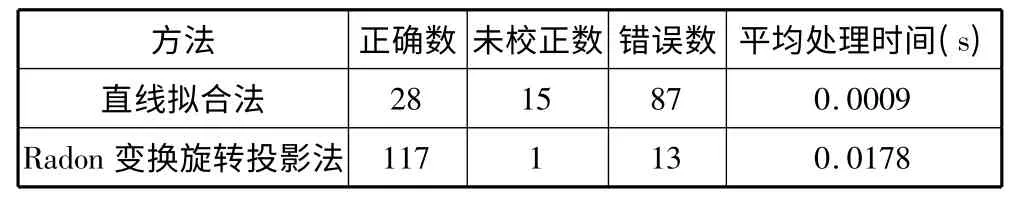
表2 竖直校正测试结果

4 结束语

本文对常用的几种水平倾斜校正方法进行对比研究，并分析校正误差存在的原因，针对各种算法的不足进行改进，实验结果也表明改进方法取得了明显效果。针对现有的竖直错切校正方法设计实验进行比较，结果表明基于字符预分割理论的旋转投影方法效果较理想。

［1］包明，路小波.基于Hough 变换的车牌倾斜检测算法［J］.交通与计算机，2004，22(2):57-60.

［2］王良红，王锦玲，梁延华.改进的Hough 变换在校正汽车牌照倾斜中的应用［J］.信息与电子工程，2004，2(1):45-48.

［3］杨立刚，张兴会，李兰友.车牌照字符倾斜校正方法的研究［J］.仪器仪表学报，2004，24(S4):696-697.

［4］Wen C Y，Yu C C，Hun Z D.A 3-D transformation to improve the legibility of license plate numbers［J］.Journal of Forensic Sciences，2002，47(3):578-585.

［5］葛海江，方江江，张翔.车牌识别系统中车牌定位及倾斜矫正算法研究［J］.杭州电子科技大学学报，2007，27(2):49-52.

［6］贡丽霞，白艳萍.Radon 变换在倾斜车牌图像校正中的应用［J］.测试技术学报，2009，23(5):452-456.

［7］贡丽霞.车牌识别系统中的牌照定位及倾斜校正技术研究［D］.太原:中北大学，2010.

［8］贡丽霞，白艳萍.基于Radon 变换和坎尼边缘检测的倾斜车牌校正方法研究［J］.太原师范学院学报:自然科学版，2010，9(1):61-63.

［9］黄骥，吴一全.基于颜色对特征点主成分分析的车牌校正方法［J］.中国图象图形学报，2008，13(4):642-646.

［10］吴一全，丁坚.基于K-L 展开式的车牌倾斜校正方法［J］.仪器仪表学报，2008，29(8):1690-1694.

［11］潘梅森，郭国强.基于图像矩的车牌号码倾斜校正［J］.计算机辅助设计与图形学学报，2007，19(8):1041-1045.

［12］Pan M S，Yan J B，Xiao Z H.An approach to tilt correction of vehicle license plate［C］// Proceedings of International Conference on Mechatronics and Automation，2007.2007:271-275.

［13］Paunwala C N，Patnaik S，Chaudhary M.An efficient skew detection of license plate images based on wavelet transform and principal component analysis［C］// Proceedings of the International Conference on Signal and Image Processing，2010.2010:17-22.

［14］Pan M S，Xiong Q，Yan J B.A new method for correcting vehicle license plate tilt［J］.International Journal of Automation and Computing，2009，6(2):210-216.

［15］HU Hao.An algorithm for vehicle license plate tilt correction based on line fitting method［C］// Proceedings of the International Conference on Information Engineering，2010.2010:162-166.

［16］Wang Y f，Xu P.Vehicle license plate tilt correction based on the weighted least square method［C］// Proceedings of the 2010 IEEE International Conference on Computer Science and Information Technology.2010:126-130.

［17］雷超阳，刘军华，李桥.基于SOM 神经网络聚类的车牌号码倾斜校正算法［J］.计算机工程与设计，2009，30(14):3406-3408，3413.

［18］潘仁龙，马晓娟，王林.基于方向场的车牌倾斜校正方法［J］.贵州科学，2011，29(2):85-88.

［19］Pan R L，Ma X J，Wang L.An efficient method for skew correction of license plate［C］// Proceedings of the 2nd International Workshop on Education Technology and Computer Science.2010:90-93.