激光偏振干涉纳米定位系统的设计与实验研究*

许素安，钱 飞，谢 敏，黄艳岩，富雅琼，陈 乐，孙 坚

(中国计量学院机电学院，杭州310018)

当前，在现代机械加工、生物工程、纳米科学与技术、先进光学器件及半导体等领域的推动下，精密测量与精密加工的精度水平正从微米量级向纳米量级以至亚纳米量级过渡。直接决定精密测量与加工精度的超精密定位方法与技术是这些领域的研究重点之一［1－5］。精密定位多采用电容测微仪，光栅，激光干涉仪。电容测微仪和光栅虽然能够实现纳米甚至是亚纳米的测量分辨率，但从溯源性角度考虑，仍需用激光干涉仪进行标定和校准。因此，在现代超精密加工中，激光干涉仪由于具有可溯源性、抗干扰能力强、无限高分辨率等特点，被广泛使用［6－10］。

激光干涉仪可分为单频激光干涉仪和双频激光干涉仪。在精密测量中，双频激光干涉仪以其测量稳定、抗干扰能力强、分辨率高等特点逐渐取代单频激光干涉仪，但单频激光干涉仪仍有其固有的优点如光路简单，成本低和周期性误差小。对于激光干涉仪系统，一旦经典误差源(如激光稳定性、线性误差、温度波动、机械振动)被抑制在一定范围，干涉仪的主要非线性误差则来源于光学偏振混叠。比如同样对于两偏振态混叠率为0.1的情况，单频激光干涉仪的误差比双频激光干涉仪约小20倍［11－12］。鉴于此，国内外研究机构和生产厂商又重新将眼光投向单频激光干涉仪，致力于单频激光干涉仪测量分辨率的提高研究。如Heidenhain公司的单频激光干涉仪(ILM311)的分辨率为0.15 nm;美国国家标准技术研究院(NIST)利用光学倍频细分法获得了0.1(0.7 nm的分辨率;我国清华大学利用组合频率解调法获得了0.49 nm的分辨率［13－14］;天津大学研制了干涉条纹8细分法的单频激光干涉仪，其分辨率为0.16 nm［15］;哈尔滨理工大学研发了基于偏振光的集成式单频激光干涉仪，其分辨率可达 10 pm/Hz1/2［16］。

本文提出了基于偏振光干涉的纳米定位系统。在传统的单频激光干涉仪的基础上，引入偏振光技术。用偏振计取代传统单频激光干涉仪的光电传感器并配置偏振分光元件、起偏镜等，可将干涉仪出射光的干涉条纹相位细分为36 000份，使用波长为633 nm的激光源，可将理论测量分辨率提高到10 pm。本文还就实现的纳米系统进行了实验研究和误差分析，分别给出了余弦误差、阿贝误差、激光源频率稳定性、空气折射率误差和出射光偏振态线性误差等各误差源的不确定度值。

1 激光偏振干涉测量位移原理

激光偏振干涉测长原理如图1所示。激光源的出射线性偏振光其偏振角为45°，该偏振光经偏振分光镜被分成两束:即P偏振光和S偏振光。P偏振光经λ/4玻片后变成圆偏振光被发送至固定镜，S偏振光经λ/4玻片后变成圆偏振光被发送至移动镜，该两束偏振光分别经固定镜和移动镜反射，依次通过λ/4玻片、偏振分光镜PBS后，成为两圆偏振光，最后经λ/4成为线性偏振光，被发送至偏振计。

图1 激光偏振干涉测长原理

测量光束在干涉仪输出处的电矢量方程为:

当移动镜移动时，测量光束相位角的变化量值为±φ，正负符号取决于移动镜的移动方向。测量光束的电矢量方程变为:

干涉仪出射光的总电矢量方程为:

因此，干涉仪出射光归一化琼斯矢量为:

干涉仪出射光束为线性偏振光，方位角θ与相位变化量Φ有关。移动镜的位移量可通过测量偏振平面的方位角θ来测量，位移量Δx与方位角变化量Δθ的关系可表达为:

式中λ0为真空激光波长，n为空气折射率。

方位角θ可由偏振计测量，其分辨率为0.01°，则针对633 nm波长源，位移测量可能达到的分辨率为17 pm。

2 激光偏振干涉纳米定位系统

偏振干涉纳米定位系统的结构图如图2所示，激光源出射光为线性偏振光，该线性偏振光的方位角为45°(实际可由线性偏振片和λ/2玻片组合调节而成)。移动镜固定于压电陶瓷(Thorlabs AE0505D16)上，该压电陶瓷对应于±20 V电压的最大行程为±1.5 μm，压电陶瓷由可编程电压源驱动。干涉仪的出射光发送至偏振计的传感单元，该传感单元通过串口线与偏振计的数据采集单元相连。PC机通过RS232串口实时采集由偏振计测量得到的方位角数据。实验室用的商用偏振计(Thorlabs－PA410)测量方位角，其测量分辨率为0.01°，因一个周期360°对应的位移量值为一个波长值λ，则该干涉仪的位移测量分辨率可达λ/36 000。整个实验系统安放于气浮隔震实验台上。实验室安装有小型环境监测仪以监控实验室内的温度(PT100，1σ =0.01 ℃)，压力(Paroscientific 1σ=3 Pa)和湿度(HygroM4，1σ=1%)的变化。

图2 激光偏振干涉定位系统结构图

为了验证自研单频偏振干涉仪的测量能力及理论推导的正确性，我们将自研的偏振干涉仪与商用单频干涉仪(SIOS－SP2000TR)的测量结果进行对比。其实验装置图如图3所示。偏振干涉仪与SIOS干涉仪测量同时测量安装于压电陶瓷执行器上的移动镜，该移动镜为双面移动镜。SIOS干涉仪的其中一束光束与偏振干涉仪的激光束共轴。值得一提的是两干涉仪的参考镜不是同一个，SIOS干涉仪的移动镜位于其测量头内，因此，两干涉仪的测量光路不同，故很难用该测量装置来测量大行程的位移。我们在短行程上将两干涉仪的测量结果做了比较，其实验结果如图4所示。另外，压电陶瓷的灵敏度为(75 nm/V)，欲得到理论值为10 nm步距值的位移，其步进驱动电压为0.13 V。该电压源为可编程电压源(Thorlabs－BPC301)，通过USB接口与PC机相连，自编的LabView软件可控制电压源的电压产生幅值和频率，图4的测量图对应的压电陶瓷的电压产生频率为0.1 Hz。

图3 偏振干涉仪与商用干涉仪位移测量装置照片

图4为压电陶瓷理论步进值为10 nm的两干涉仪测量结果，偏振干涉仪的测量曲线，其采样频率为2 Hz且数据未作均值处理。SIOS干涉仪的测量曲线，其采样频率为128 Hz且在64 bit数值上做平均处理。从图4可以看出，两干涉仪的测量结果基本拟合，考虑到两干涉仪不同光路，很难对实验结果做量化对比。

图4 偏振干涉仪与SIOS干涉仪位移测量实验结果

3 纳米定位系统实验研究与误差分析

激光干涉测长的测量精度容易受多种因素的影响，如机械误差、光学误差和环境误差。我们对这些误差源逐一进行了量化，并且特别给出了偏振干涉仪出射光的偏振态对位移测量的影响。

3.1 余弦误差

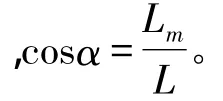
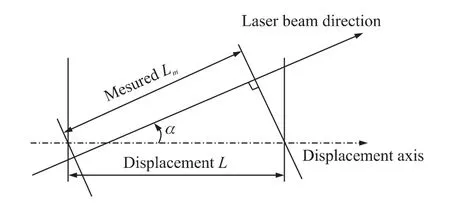
图5 余弦误差示意图

3.2 阿贝误差

当被测轴线与反射镜运动轴线不重合时，反射镜沿镜面中心的微小偏转会引起阿贝误差，如图6中E所示，当E→0时，阿贝误差E可近似的表示为E≅hα，h为阿贝臂。由此可见由俯仰角或摇摆角引起的阿贝误差与阿贝臂h成线性关系。

图6 阿贝误差示意图

我们实验系统中的俯仰角和摇摆角由商用单频干涉仪(SIOS SP 2000－TR)测得，偏转角的测量范围为±2 arcmin，测量分辨率为0.02 arcsec。俯仰角和摇摆角的测量结果如图7所示。

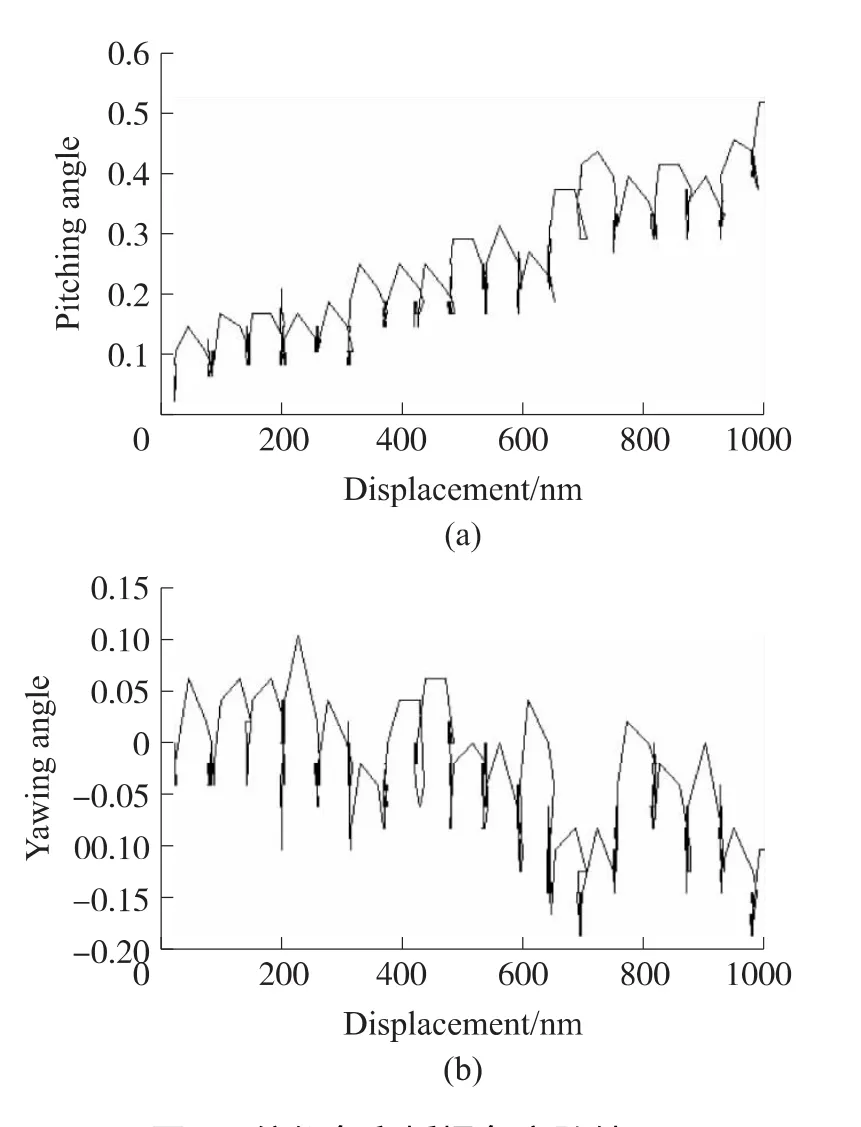
图7 俯仰角和摇摆角实验结果

图7(a)所示为俯仰角测试结果图，由图7(a)可知，压电陶瓷在1 μm行程上的俯仰角为0.5″(2.4 μrad)。图7(b)所示为摇摆角测试结果图，由图7(b)可知，压电陶瓷在1 μm行程上的摇摆角为0.3″(1.5 μrad)。对于我们的单频激光偏振干涉定位系统，很难测量阿贝臂的精确值，但其最大估计值为0.2 mm。因此，由俯仰角和摇摆角引起的阿贝误差分别为E=0.5 nm和E=0.3 nm，我们可得定位系统的阿贝误差为0.8 nm。

3.3 干涉仪出射光偏振态的影响

为研究激光束的偏振态对位移测量结果的影响，我们调节图2示例中置于偏振计前的λ/4玻片。干涉仪出射光的偏振态可随λ/4玻片的旋转方位角的改变而改变。图8为不同偏振态条件下的位移测量实验结果。压电陶瓷的步进驱动电压为0.7 V，相应的压电陶瓷理论步进位移值为70 nm。图6中实线对应的椭偏角ε=0°，虚线对应的椭偏角ε=10°，由图可知，虚线和实线终点处的差值为ε=20 nm。因此，在实验前，应确保干涉仪的出射光为线性偏振光(ε=0°)。经20次重复性实验表明，经来回行程后其起、始点的差值小于1 nm。

图8 激光束偏振态对位移测量的影响

3.4 激光源频率稳定性

实验所用激光源为单频633nm波长光源(Renishaw ML10)，ML10激光源可溯源于国家标准。其频率长期稳定性为10－7，也就是说对于100 μm行程位移，其测量误差值小于10 pm，因此该误差值对于我们的定位系统可忽略。

3.5 空气折射率误差

与所有的干涉仪一样，我们的偏振干涉仪的测量结果也受到空气折射率n的影响。该折射率主要与环境温度、气压、湿度和CO2含量有关。

如测量是在标准实验室条件下进行，即大气压强为101 325 Pa，环境温度为 20℃，水蒸气压为1 170 Pa(h≈50%，Tamb=20℃)，CO2含量为450×10－6。国际上通用的空气折射率计算公式为:

标准空气折射率(n－1)s与波长数σ(μm－1)有关，对于波长范围在350 nm＜λ＜650 nm时，σ介于1.538和2.587之间。对于严格环境控制的实验条件，空气折射率不确定度的最优值可为10－8。在标准实验室环境条件下，空气折射率不确定值可控制在10－5至10－6。对于微米级行程的位移，其测量不确定度可控制在皮米(pm)级。

3.6 定位系统误差评定

根据以上的分析，表1总结了本定位系统的主要误差源对应于位移量d的测量不确定值。

表1 定位系统误差分析表

4 结论

［1］ 许素安，Luc Chassagne，Suat Topcu，等.偏振激光干涉仪的纳米定位系统［J］.中国计量学院学报，2009，20(2):118－121.

［2］ Xu S，Ouedraogo K，Chassagne L，et al.Polarimetric Interferometer for Nanoscale Positioning Applications［J］.Review of Scientific Instruments，2008，79，125104:1－6.

［3］ Xu Suan，Chassagne Luc，Topcu Suat，et al.Phase Control of Ellipsometric Interferometer for Nanometric Positioning System［J］.Science China Technological Sciences，2011，54(12):3424－3430.

［4］ 李志全，吴朝霞，唐旭晖.双干涉式微位移测量系统的研究与性能改善［J］.传感技术学报，2009(3):216－219.

［5］ Chassagne L，Wakim M，Xu S，et al.A 2D Nano-Positioning System with Sub-Nanometric Repeatability over the Millimeter Displacement Range［J］.Measurement Science and Technology，2007，18:3267－3272.

［6］ 张立新，黄玉美，杨心刚，等.回转轴运动精度的干涉测量与误差补偿分析［J］.传感技术学报，2007，20(3):216－219.

［7］ 许素安，李东升，Chassagne Luc，等.基于外差干涉技术的纳米定位方法［J］.仪器仪表学报，2011，32(7):1655－1659.

［8］ 李立艳，王坚，韩春阳，等.用于纳米测量的集成化单频激光干涉仪［J］.中国激光，2011，38(4):0408001－1:6.

［9］ 齐永岳，赵美蓉，林玉池，等.高精度单频激光干涉仪的设计与实验研究［J］.传感器与微系统，2009，28(4):50－53.

［10］张立新，黄玉美，杨心刚，等.回转轴运动精度的干涉测量与误差补偿分析［J］.传感技术学报，2007，20(3):686－689.

［11］黎永前，李晓莹，朱名铨，纳米精度外差式干涉仪非线性误差修正方法研究［J］.仪器仪表学报，2005，26(5):42－546.

［12］ Xu Suan，Chassagne L，Topcu S，et al.Polarimetric Interferometer for Measuring Nonlinearity Error of Heterodyne Interferometric Displacement System［J］.2013，11(6):061201:1－5.

［13］ Bobroff N.Recent Advances in Displacement Measuring Interferometry［J］.Measurement Science and Technology，1993(4:907－926.

［14］ 所睿，范志军，李岩，等.双频激光干涉仪技术现状与发展，2004，34(4):251－253.

［15］曲兴华，王丽华.基于激光技术的亚纳米级位移测量系统的研究［J］.仪器仪表学报，2010，31(6):1276－1281.

［16］李立艳，王坚，韩春阳.用于纳米测量的集成化单频激光干涉仪［J］.中国激光，2011，38(4):0408001－1:6.