WSN中的分布式压缩感知

吕方旭，张金成*，石洪君，王 泉，王 钰

(1.空军工程大学防空反导学院，西安710051;2.空军大连通信士官学校信息网络系，辽宁大连116600)

无线传感器网络WSN(Wireless Sensor Network)是由具有传感能力、计算能力和无线通信能力的微型节点，以无线多跳路由方式通信的自组织网络。它能够协作地实时监测、感知和采集各种环境对象的信息，在军事和民用中应用非常广泛［1－3］。然而无线传感器网络体积小、携带能源有限，因此其计算、存储、通信能力都比较弱，当大规模部署时，整个网络的生存周期比较短。在信息驱动的协作跟踪［4］时，如果将原始数据发送到处理能力较强的簇头中计算，终端节点的通信能耗开销增大，整个网络的生存周期非常短。如何在保证监测信息不丢失的同时，降低数据传输量，是降低通信能耗的一种主要手段。近年来提出的压缩感知［5－8］(Compressed Sensing)技术，其以远低于奈奎斯特采样定理的情况下获取少量数据，然后利用重构算法对原始信号进行恢复，这为资源受限节点的采集和通信能耗的降低提供了解决办法。文献［9］利用压缩感知理论将节点采集得到的数据进行压缩传输，降低了通信能耗;文献［10－11］利用时空压缩感知的办法将多个节点采集的数据进行联合压缩传输，进一步降低了通信能耗，但这些都不是真正意义上的压缩感知。文献［12］进行了压缩采样的研究。由于传统压缩感知技术的实现对硬件资源要求比较高［13］，无法直接将其应用于节点资源受限的无线传感器网络。文献［14］提出了一种较好的解决思路，即随机压缩采样的思想。

本文主要研究了随机压缩采样的实现方法和分布式压缩感知这两方面的内容。首先，在研究随机压缩采样的基础上，提出了用定时器控制ADC进行随机压缩采样的实现方法，实验表明该方法有效可行。然后，提出了分布式压缩感知算法。该算法将随机压缩采样序列根据节点合理拆分，由各节点按采样子序列进行采样，最后利用各节点的采样值和CoSaMP算法实现对原始信号的精确重构。

1 压缩感知理论概述

压缩感知是Donoho等人在2006年开创的信号处理新理论。压缩感知的基本思想是将压缩与采样合并进行，首先采集信号的非自适应线性投影，即计算信号的测量值。然后根据相应的重构算法由测量值重构原始信号数据。若测量值的数据小于原始数据，则能获得压缩数据量的效果。它主要包括信号的稀疏表示、观测矩阵设计和信号重构3个方面。

压缩感知的先决条件是信号是稀疏的或者信号在某种变换下可以稀疏表示。即在一个信号中或者信号在某种变换下，如果只有k个元素是非零的，则该信号是k稀疏的。一般来说，普通的信号在时域都是非稀疏的。因此，要应用压缩感知，首先要对信号进行变换，以找到信号的稀疏域，一般信号在小波基、傅里叶基和余弦基中都是稀疏的。

观测矩阵就是对信号的一种获取方式，它的设计是压缩感知的主体，从物理上可以理解为信号在观测矩阵下的信号获取，信号也在投影的过程中被压缩。寻找一个满足约束等距性RIP(Restricted I-sometry Property)条件的观测矩阵Φ∈RM×N(M≪N)，对信号x执行一个压缩观测，即:

就可以得到M个线性观测y∈RM，这些少量线性投影中包含了重构信号x的足够信息。各分量表示如图1所示。

但是有限等距离性质的等距离常量是很难计算的，文献［8］指出，只有Donoho提出的相关性判别理论，即互相关系数可以较为直观的判别某一测量矩阵的形态。互相关系数可以由式(2)求得:

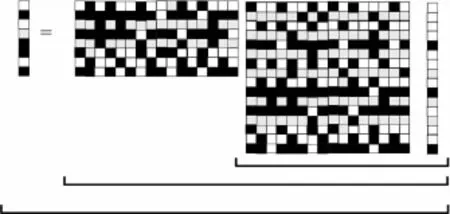
图1 压缩采样各分量示意图和矩阵表示

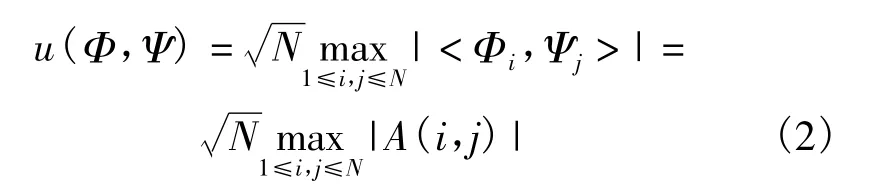
信号重构是已知测量值y和测量矩阵Φ来恢复原始信号x。从y中恢复x是一个解线性方程组的问题，从方程(1)上看，这似乎是不可能的，因为这是一个未知数大于方程个数的病态方程，存在无穷多个解。但是x在Ψ下可以稀疏表示，记CS信息算子ACS=ΦΨ，因此式(1)可以表示为

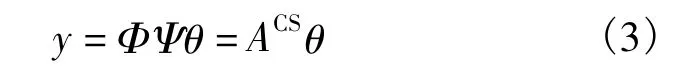
虽然从y中恢复θ也是一个病态问题［15］，但是因为系数θ是稀疏的，这样未知数个数大大减少，使得信号重构成为可能。文献［16］认为:只要矩阵ACS满足RIP条件，则可以证明θ可以通过求解最优l0范数问题精确重构，即:

式中，‖·‖0表示l0范数，即向量θ中非零元素的个数。

2 随机压缩采样

2.1 随机压缩采样的基本思想

传统的压缩采样工程实践［12］是利用M路ADC对信号进行随机线性投影来进行压缩采样，它是通过构建多路平行的信号采集支路，每个支路均由随机信号发生器和积分电路组成，其中随机信号发生器必须产生足够高频率的服从伯努利分布的±1信号。这种方法虽然降低了采样速率，但随机信号发生器仍需在奈奎斯特频率下产生随机数，不但增加了能量而且硬件实现较高，在无线传感器网络中无法直接使用。文献［14］的随机压缩采样，为压缩感知在无线传感器网络中的应用提供了思路。

本文在随机压缩采样理论的指导下提出用定时器控制ADC进行随机压缩采样，即定时器按照随机采样序列对波形进行随机抽取。如图2所示，图2(a)是传统的采样过程，它利用等间隔的采样序列对信号采样，其过程可以看作是信号在标准单位矩阵I(I是等间隔采样序列的矩阵表示形式)上的投影;图2(b)是随机压缩采样过程，它利用随机采样序列对信号采样，其过程可看作是信号在Sample(Sample是随机采样序列的矩阵表示形式)上的投影。

图2 两种采样过程

随机压缩采样过程中，利用一路ADC，根据随机采样序列对信号进行随机抽取，然后将采样值xd在观测矩阵Φ中投影，最后利用重构算法进行重构，各分量的矩阵表示如图3所示。

图3 随机压缩采样各分量示意图和矩阵表示

在这里我们定义随机采样率为:

其中Ttotal表示采样时间，M表示这段时间内随机采样的个数。

2.2 无线传感器网络中的随机压缩采样技术

本节研究了无线传感器网络中压缩感知技术的实现方法。无线传感器网络中，终端节点一般由包含传感能力、处理能力和无线通信的微小节点组成。目前常用的集成芯片有CC2430、CC2530等，由它组成的节点的资源和计算能力非常有限，但它内部含有较高精度的定时器，可以完成随机压缩采样任务;簇头节点一般具有较大的存储空间且可包含DSP芯片，能够完成较为复杂的重构算法。其信号处理流程图如图4所示。

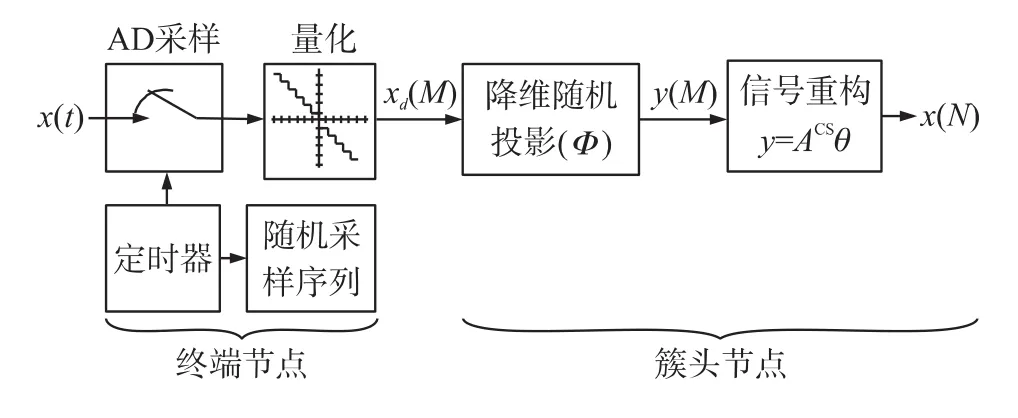
图4 无线传感器网络中的压缩感知流程图

具体步骤如下:

第1步 在簇头中生成随机采样序列ti，i∈{1，2，…，M}，其中 t0=0，ti=ti－1+ τ，τ 满足 N(N/M，M2K2/N2)的高斯分布，且τmin＞TADC(即随机压缩采样的最小采样间隔必须大于ADC的最小采样周期)。这里N/M代表不同稀疏度下的平均采样间隔，K为信号的稀疏度，M为该稀疏度下随机压缩采样次数。存储随机采样序列，并发送一份拷贝到簇头节点;

第2步 在终端节点中，定时器根据采样序列控制ADC进行随机压缩采样，获取随机采样值xd(M)，并将其发送至簇头节点;

第3步 在簇头节点中，接收xd(M)，然后根据随机采样序列 ti，i∈{1，2，…，M}，将 xd(M)内插(N－M)个0，得到 xd(N)，并在观测矩阵 Φ∈RM×N中进行降维随机投影，最终获得y(M);

第4步 在簇头中根据y(M)和ACS利用Co-SaMP重构算法进行重构。

在实际的应用中，随机压缩采样一定要注意的关键问题，即生成的随机采样序列的最小间隔必须大于ADC的最小采样周期，这样才能保证ADC的正常工作。

2.3 无线传感器网络中单节点的随机压缩采样实验

实验平台使用TI提供的CC2530芯片和ZStack－CC2530 －2.3.1 －1.4.0 协议栈。终端节由包含CC2530芯片的节点和外围电路组成，簇头由包含CC2530芯片的协调器和PC机组成。采集过程在终端节点中完成;重构算法在PC机中的MATLAB中完成，簇头中包含CC2530芯片的节点，负责数据和命令的无线收发。实验结构拓扑图如图5所示，其中B节点时终端节点，节点A和PC机组成簇头节点。

图5 实验结构拓扑图

实验中，ADC选用11 bit的量化精度，其采样周期 TADC=68 μs［17］，原始信号是由 F40 型数字合成函数信号发生器产生的正弦信号，频率是5 kHz，Vpp=800 mV，直流偏置是500 mV。随机采样点数M=50，恢复信号的采样频率是Fs=25 kHz，长度N=300。观测矩阵是M×N的随机矩阵，稀疏基是N×N的傅里叶基。ADC的等效采样频率faverage≈4.1 ksample。

实验结果如图6所示。图6(a)是从示波器测得输入信号波形的放大图，图6(b)是示波器观察原始信号的频谱和全局波形图，图6(c)是ADC随机采样后，发送到PC机在MATLAB中显示的随机采样波形图，图6(d)是随机采样波形和重构信号波形的对比，图6(e)是重构信号的全局波形图，图6(f)是重构信号的频谱图。

本实验根据4.1 ksample的采样频率下获取的少量的随机测量值，如图6(c)所示，重构出5 kHz的正弦信号(e)。从图6(a)和6(e)可以看出，重构信号的幅值和原始信号基本相同;从图6(b)和6(f)可以看出重构信号的频率没有失真。实验结果表明，在无线传感器网络中，利用定时器控制ADC进行少量随机测量后，可以实现对信号的准确重构。同时，本实验结果表明，利用低速的单个ADC对高频信号的获取是可行的。

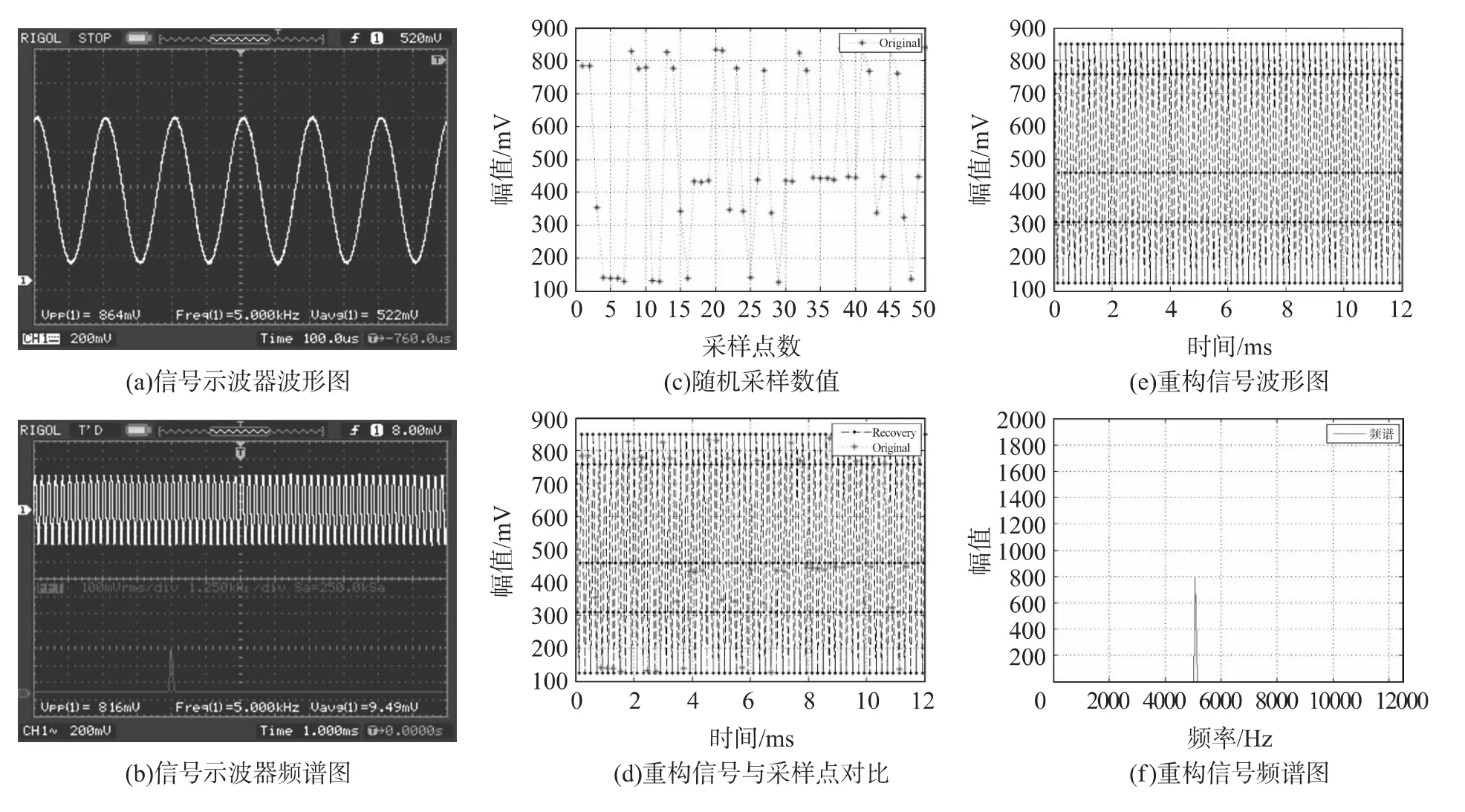
图6 压缩感知信号实验图

3 分布式压缩感知

3.1 分布式压缩感知模型

根据随机压缩采样的物理过程，如图2(b)所示，可将含噪信号的随机采样模型表示为:

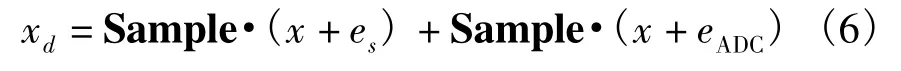
其中xd为随机压缩采样后的观测值，Sample为随机采样矩阵，es表示采样前信号混入的噪声，eADC表示ADC的量化噪声。本文在研究过程中假设es和eADC都是白噪声，且将式(6)化简为:

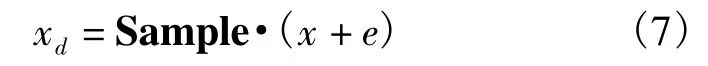
在分布式压缩采样过程中，首先将Sample拆分成r(r表示节点个数)个子矩阵，节点根据拆分后的采样序列进行随机采样;然后将各节点的采样值按拆分规则进行组合，得到随机观测值xd;最后将xd在观测矩阵上进行投影，得到压缩观测值y。其模型如下所示:

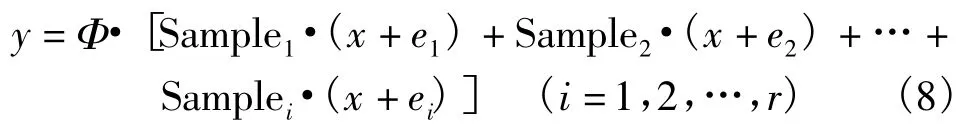
式(8)中Samplei表示第i个节点的随机子采样序列，ei表示第i个节点采样时的噪声，其中Sample=Sample1∪Sample2∪…∪Samplen且Ø =Sample1∩Sample2∩…∩Samplen。

3.2 无线传感器网络中的分布式压缩感知技术

在分布式压缩感知模型的指导下，结合1.3节描述的硬件平台，本节具体讨论了无线传感器网络中分布式压缩感知的实现方法。具体步骤如下:

第1步 在簇头中生成随机采样序列ti，i∈{1，2，…，M}，其中 t0=0，ti=ti－1+ τ，τ满足 N(N/M，M2K2/N2)的高斯分布，且 ti－ti+r＞TADC(即随机压缩采样序列的间隔r个的差值必须大于ADC的最小采样周期)。

第2步 根据式(8)，将随机采样序列拆分成r个随机采样子序列tj×r+n(i=j×r+n，i是随机采样序列的下标，j是随机采样子序列的下标，r是节点的总数，n是节点的序号)，并将其发送至各终端节点。

第3步 在各终端节点中，定时器根据各自收到的随机采样子序列控制ADC进行采样，得到随机采样值xdn(M')(表示第n个节点的随机采样值，长度为M'=M/r)，并将其发送至簇头节点。

第4步 簇头根据拆分规则生成联合随机采样序列 xd(M)，然后根据随机采样序列 ti，i∈{1，2，…，M}，将xd(M)内插N－M个0生成xd(N)，最后在观测矩阵Φ∈RM×N中进行降维随机投影，获得压缩值y(M);

第5步 在簇头中根据y(M)和ACS利用Co-SaMP算法进行信号重构。

对比1.3节的随机压缩采样步骤，分布式压缩感知步骤中增加了随机采样序列的拆分和测量值的组合。在实际应用中，为了保证ADC的正常工作，同样拆分后随机采样子序列的最小间隔必须大于ADC的最小采样周期。从3.1节可知，在采样序列一定的情况下，随着节点数的增加，各节点的采样子序列间隔会增加，且远大于ADC的采样周期，因此分布式压缩感知算法比单路ADC的随机压缩采样适用范围更广，可以在更低采样速率下完成高频率信号的采集。

在实际应用中，分布式压缩感知算法同样存在问题，虽然节点中高精度的定时器能够控制ADC严格按照采样序列采样，但多个节点能否按照采样序列进行协同采样是分布式压缩在实际应用中要解决的问题。实际上，只要保证在每一次采样时，各个节点中的定时器能够同时启动就能实现他们之间的协同采样。在临时簇中，由于参与分布式压缩感知的节点与簇头的距离都比较近，因此在确保分布式节点进入准备采集状态后，簇头通过发送脉冲命令帧的方法同时启动星型网络中各节点的定时器。

3.3 分布式压缩感知仿真实验

本节仿真实验对比了分布式压缩采样机制和传统压缩采样机制的重构效果。分布式压缩采样实验中，2个节点参与分布式压缩采样，由于分布式探测目标时各节点距离目标的位置不同，因此假设节点的信噪比分别为30 dB、40 dB。信号源是5个正弦信号的叠加，频率分别为 300 Hz、700 Hz、2 kHz、9 kHz和12 kHz，幅值为0.5～1的随机数，相位是0～π之间的随机数。压缩采样过程中，采样序列长度M=50，子序列长度为25，恢复信号的采样频率Fs=25 kHz，长度N=250。观测矩阵是M×N的随机矩阵、稀疏基是N×N的傅里叶基。单节点的等效采样率faverage≈2.5 ksample。传统压缩采样实验中，节点的信噪比35 dB，原始信号、观测矩阵和稀疏基都同分布式压缩感知相同，等效采样率 faverage≈5 ksample。图7和图8分别是两种压缩采样的重构结果。

对比可以发现，分布式压缩采样保留了原始信号有用的信息，因而在重构过程中能够保证较高的重构精度。分布式压缩感知的重构精度没有经典压缩采样的重构精度高，那是在采集时，两节点有10 μs左右的启动延迟，但它依然能够在包含优30 dB的输入信噪比时达到10－3的量级，同样保证了很高的重构精度。最重要的是，在不同输入信噪比的情况下，分布式压缩感知能够以远低于随机压缩采样的采样速率实现精确重构。

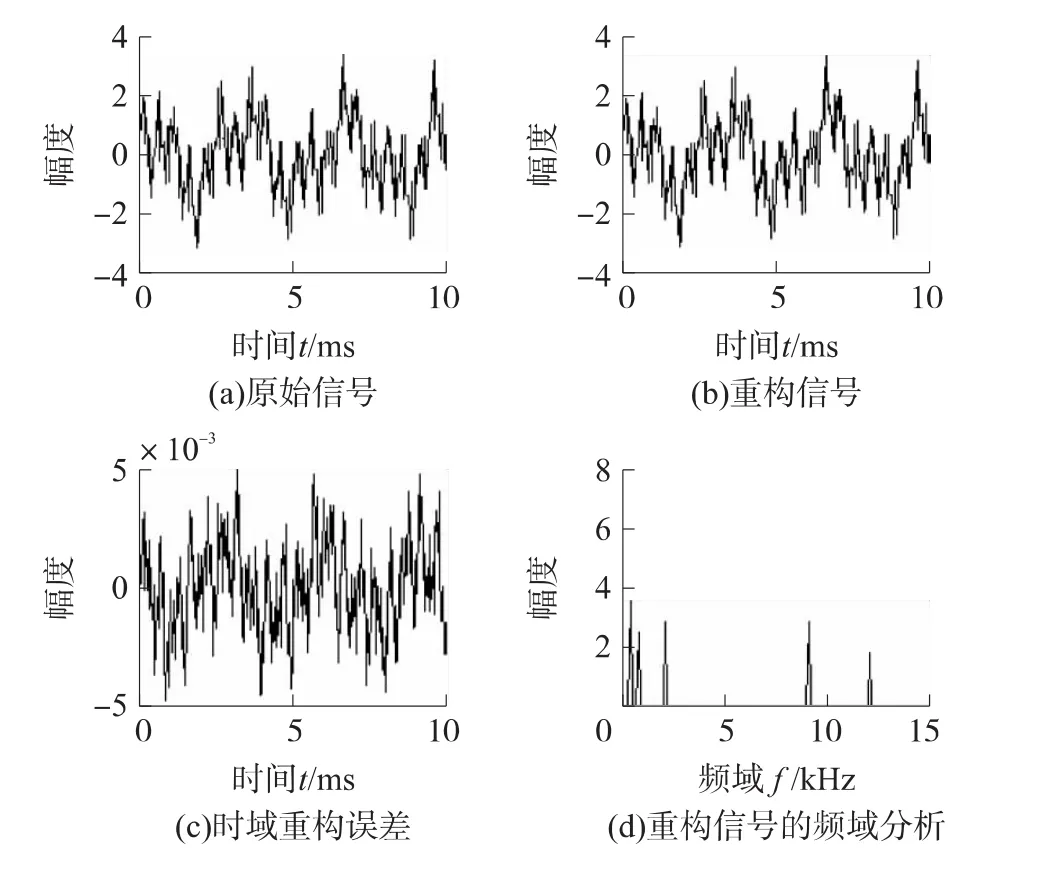
图7 分布式压缩采样重构结果

图8 经典压缩采样重构结果

3.4 无线传感器网络中的分布式压缩感知实验

实验中两个节点参与分布式压缩感知，两节点的启动延迟可以达到2 μs以下，其余实验平台同2.3节描述一样，结构拓扑图如图9所示。PC机和节点A作为簇头，完成采样子序列的分发，采样值的接收以及信号的重构;终端节点B和C是分布式采样的两个节点，它们各自在定时器的控制下按照随机采样子序列进行采样。实验中，ADC选用11 bit的量化精度，其采样周期TADC=68 μs，原始信号是信号源产生的5 kHz正弦信号，幅值Vpp=800 mV，直流偏置500 mV。每个节点的随机采样个数是25个，恢复信号的采样频率是Fs=25 kHz，长度N=250。观测矩阵是M×N的随机矩阵，稀疏基是N×N的傅里叶基。节点中ADC的等效采样频率faverage≈2.5 ksample。

图9 实验结构拓扑图

实验结果如图10所示。

实验中根据两个节点以2.5 ksample的采样速率随机抽取了25个值，如图10(b)所示，重构出以25 ksample采样率采集的5 kHz的信号，如图10(c)所示。从图10(a)和图10(c)可以看出，重构信号的幅值和原始信号基本相同;从图10(a)和图10(d)可以看出重构信号的频率没有失真。实验结果表明，本文提出的分布式压缩感知算法，能够在星型网络拓扑结构中以1/10的标准采样率下获得的少量数据实现信号的精确重构。

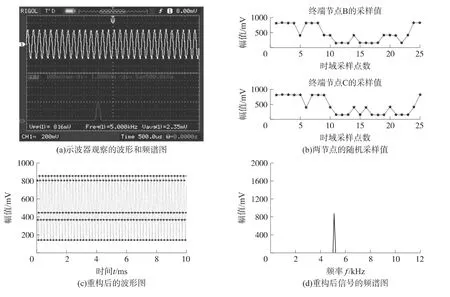
图10 分布式压缩感实验结果

4 结论

本文针对压缩感知在无线传感器网络中的应用，首先在分析随机压缩采样思想的基础上提出了用定时器控制ADC进行随机采样的方法，然后提出了分布式压缩感知算法。该算法将压缩感知理论应用于无线传感器网络平台，即在少量的观测数据下实现对信号的精确重构。仿真和实验结果均表明该方法具有很好的性能，具有非常重要的应用价值。

［1］ 吕方旭，张金成，刘立阳.基于WSN的多声源目标定位算法［J］.传感技术学报，2012，25(8):1121 －1125，1464 －1468.

［2］ 刘立阳，张金成，吴中林，等.基于RSSI＆DFP的无线传感器网络声源目标定位算法［J］.传感技术学报，2011，24(10):1464－1468.

［3］ 刘立阳，张金城，吴中林.基于分布式动态簇结构的WSN自适应目标跟踪算法［J］.传感技术学报，2012，25(1):110 －113.

［4］ 孙利民，李建中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005:391 －402.

［5］ Donoho D.Compressed Sensing［J］.IEEE Transactions on Information Theory，2006，52(4):1289 －1306.

［6］ Candès E，Wakin M.An Introduction to Compressive Sampling［J］.IEEE Signal Processing Magazine，2008，25(2):21 －30.

［7］ 石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37(5):1070 －1081.

［8］ 焦李成，杨淑媛，刘芳，等.压缩感知回顾与展望［J］.电子学报，2011，39(7):1651 －1662.

［9］ 胡海峰，杨震.无线传感器网络中基于空间相关性的分布式压缩感知［J］.南京邮电大学学报(自然科学版)，2009，29(6):12 －22.

［10］周四望，林亚平.无线传感器网络中的小波方法［M］.长沙:湖南出版社，2011:9.

［11］ Bontempi G，Borgne Y.An Adaptive Modular Approach to the Mining of Sensor Network Data［C］//Proc of the SIAM International Conference on Data Mining.Newport Beach，USA，2005.

［12］ Bajwa W，Haupt J，Sayeed A，et al.Compressive Wireless Sensing［C］//Proc of IEEE International Conference on Information Processing in Sensor Networks(IPSN).Nashville，USA，2006.

［13］ Candes E J，Wakin M B.An Introduction to Compressive Sampling［J］.IEEE Singal Processing Magazine，2008，25(2):21 －30.

［14］余恺，李元实，王智，等.基于压缩感知的新型声音信号采集方法［J］.仪器仪表学报，2012，33(1):105 －112.

［15］ Candes E J.The Restricted Isometry Property and Its Implications for Compresse Sensing［J］.C R Math Acad Sci Paris，2008，346(9－10):589－592.

［16］ Donoho D L，Tsaig Y.Extensions of Compressed Sensing［J］.Signal Processing，2006，86(3):533 －548.

［17］ Texas Instruments Incorporated.CC253x System-on-Chip Solution for 2.4 GHz IEEE 802.15.4 and ZigBee Applications User’s Guide［C］//Literature Number:SWRU191AApril 2009 － Revised June 2010:133－134.