智能抽水系统中的优化模型

唐华阳，彭英萍，谭大超，石章波

（乐山师范学院数学与信息科学学院,四川乐山,614000）

0 引言

随着社会的不断进步，能源需求逐年上涨，能源短缺和资源匮乏问题已经成为大家关注的焦点和热点。我国更是一个缺水和电力供应不足的国家。虽然现在全国上下大力倡导“节约水电人人有责”，但是依然存在部分人缺乏节约和环保意识，浪费水电现象经常发生。而且，在用电高峰期不仅用电量日渐高涨，电表飞转，每个月的电费账单也猛涨，这让不少市民感觉吃不消。同时，用电量的增长还会导致电网负荷越来越重。国家供电总公司为了解决在用电高峰时段设备负荷过大的问题，实行了阶梯电价及不同时段不同电价的收费政策。本项目在不同时段不同电价的收费政策基础上，针对楼宇智能抽水系统进行建模分析，制定最优化的抽水方案，使得抽水费用尽量少。

1 问题分析

1.1 蓄水池的现状分析

目前的自动蓄水系统主要集中在对水位的探测、检测电路和控制系统的设计以及安装传感器等方面，只是判断水满溢或无水两种状态来决定抽水与否，对水量的多少没有定量描述；并且抽水的时间可以出现在任何时候，不能满足电费的最优化，也不能保证用户在每个时刻都有足够的水可用；此外，在用电高峰期还会出现负荷过大的问题，对用户而言原蓄水系统既不安全又不实惠。

国家供电总公司为了解决在用电高峰时段设备负荷过大的问题，实行不同时段不同电价的收费政策，在安全上确实起到了一定的作用，对于鼓励老百姓在非用电高峰期间用电也有积极意义，但在目前的蓄水系统上并没有体现出分段计价的优势，这是项目将解决的问题。

1.2 解决方案设计

首先考虑一天的优化情况：为便于研究，对一天进行划分，即有必要根据电费价格不同将一天分成几段。在抽水时，考虑到机器的使用寿命，连续抽水的时间不要太长，两次抽水的时间间隔也不要太短（平凡开与关也会损坏机器）。所以从抽水开始到抽水结束所用的时间要合理分配，让机器连续使用的时间尽量长，减少机器维修费用。首先对我校供水中心的蓄水池抽水机的工作时间做了相关统计，方式如下：工作时间均是以小时计算，为了统计叙述方便，我们把划分的时段长取为1小时，即将每天均划分为24个时段，在各个时段进行讨论，得出优化后的结果。最后再将每个时段的长度向两边取值得出相应的优化结果，通过比较得出效果最好的时段划分方法，从而制定相应的抽水方案。

在调查中，我们得到了14天的用户用水数据记录。为此，将原始水位数据处理成需求量，引入0-1变量限制是否在该时段抽水，以满足用户需求以及蓄水池容量为约束，以抽水费用最小为目标建立优化模型，采用lingo软件进行求解得到优化方案。考虑到每天各个时段的需求量都不相同，假设每天各个时段的用水需求量服从正态分布，根据统计结果采用matlab软件产生服从正态分布的需求量来进行预测，由于通过这样的方法产生的预测数据可能会在某一时段达不到用户的需求，所以还需根据实际情况制定进一步的调整策略满足需求才行，最后再进行优化得出最小电费及抽水方案。

2 数据收集整理

2.1 将原始数据转化成用户水需求量

原始数据只是每隔一小时的水位线以及开始抽水和停止抽水的时间，我们需将这里的数据转换到每个时间段用户的需求量，即用历史使用量近似作为需求量。

（1）若此时间段内不抽水：

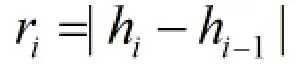
（2）若此时间段内抽水：

其中 表示第i个时间段用户对水的需求量；表示时刻i时水池中的水位线；表示单位时间段的抽水量。通过以上的公式可以把所有访问到的数据转化为用户在相应时间段内的水需求量（见表1）。

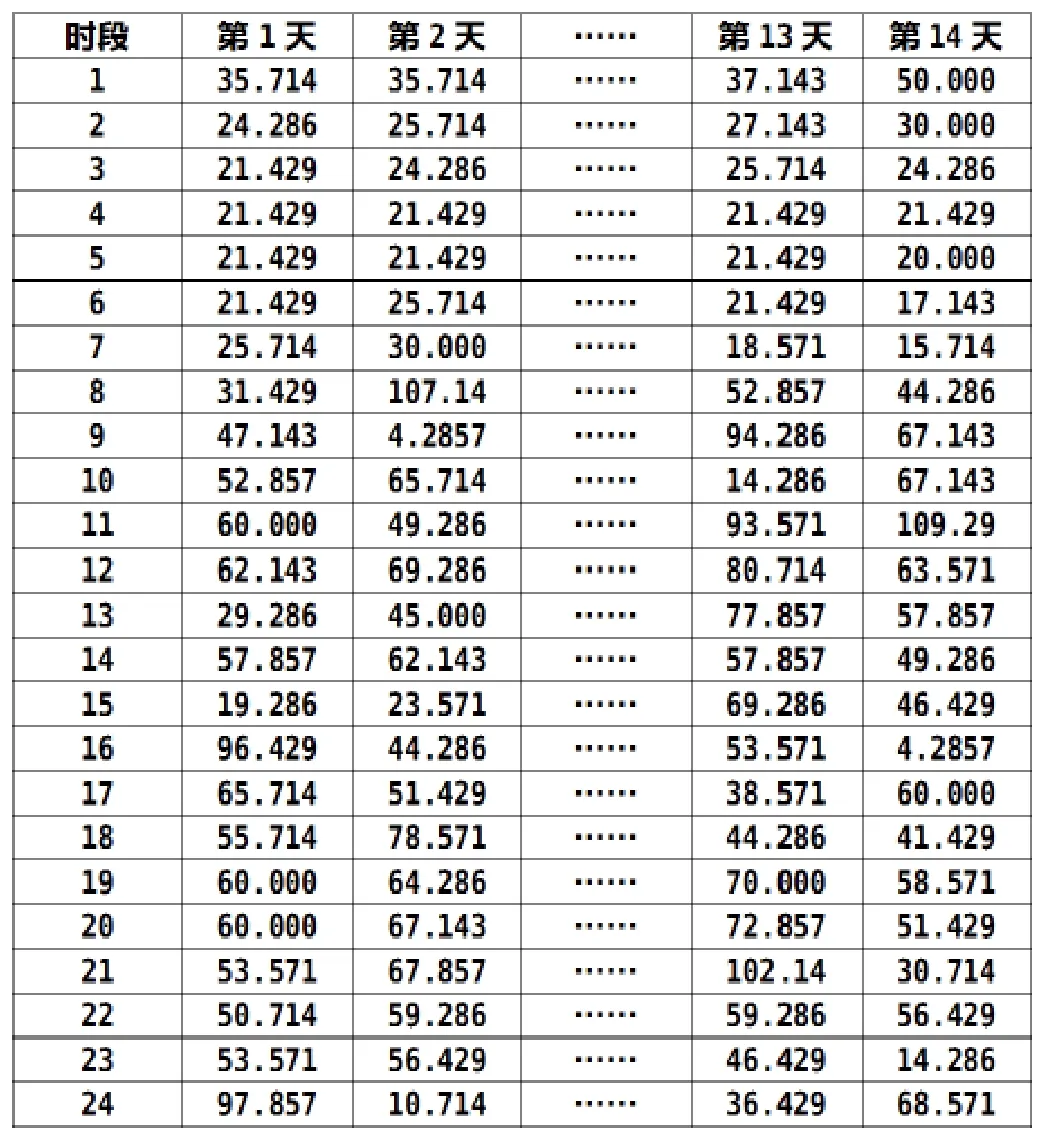
表1 部分需求量统计数据

原始数据来源于乐山师范学院自来水厂,其中第i时段表示的是从i-1时刻到第i时刻，例如时段1表示从0点到1点。

2.2 用历史需求量预测未来某天的需求量

将每天同一个时间段的水需求量数据通过以下公式进行统计，近似地计算出每天同一个时间段水需求量的期望和标准差：

3 优化模型的建立

在满足每天各个时段用水需求的情况下，应该使每天抽水的电费尽量少。因此，目标函数可表示为：

每个时间段内都能满足用户的需求，那么水池中的水加上该时段的抽水量应不低于用户的需求：

上一个时间段剩下来的水量就是下一个时间段初水池中的水量：

另外，水池的容量是有限的，所以每次抽水都不能超过水池的容积：

综合上述公式得到分时段抽水的优化控制模型，将数据带入即可求得智能抽水策略，即那些时段抽水、抽多长时间，那些时段休息等信息。

4 模型求解及结果分析

根据上述模型分别取初始水量为0、100、200、300、400、500通过Lingo编程求出结果如表2(其中假设水泵的功率为15千瓦)。

表2 第8天不同初始水量的费用以及抽水情况

从表中可以看出，当初始水位为0时，抽水方案为0-3时连续抽水，3-4时不抽水，4-5时抽水，5-11时不抽水，……，22-23时抽水，23-24时不抽水，抽水费用为69.3元。

通常情况下抽水是水位线降低时抽水，较高时停止抽水。我们将一天分为n1个抽水时段，记C为不使用优化模型的费用， 为第i个抽水时间段电费的平均单价， 为第i次停止抽水的时间， 为第i次开始抽水的时间，不使用优化模型时的电费应为：

通过计算可得在第5天，初始水位为300时使用优化模型的抽水费用为59.443元，通常情况下抽水费用为83.250元。从中可以看出，使用该优化模型比不使用时的电费每天能减少13.807元，每月能减少414.21元，每年能减少5039.555元。

5 模型改进

由于使用优化模型时需要知道每天各个时段的用水需求量，然而一个地方每天各个时段的用水量并不完全相同，而且未来的用水量也并不清楚，只能根据之前的数据来进行预测，然后再采用优化模型，从而制定抽水方案。为了便于比较，我们采用前13天的数据来预测第14天的数据。根据2.2中的预测方法得到预测效果对比图如下：

注：其中红色为对第14天的预测值，蓝色为第14天的真实值。

可以看出预测值与真实情况是有差别的，尤其是在第11时段附近，差异非常巨大。预测的水需求量和实际用水量产生差异的原因有很多：比如某一时间段发生一些意外情况(突然有别的用途增加用水量，水管爆裂等)。为了减少这种差异，我们在此预测的基础上制定了如下局部调整策略：

2)对当前时刻前n个时间段用水需求量做一个灰色预测，预测当前时刻后m个时间段的水需求量；

3)如果在m个时间段内，优化模型所计算的结果不进行抽水，或者抽水时间段数小于m，而通过灰色预测得到的结果是水池中的水加上抽到水池中的水都不能满足用户需求，那么就增加抽水时间段，直至满足用户需求。

采用前面的局部调整策略，n取值为6，m取值为2，得到调整后的预测对比图如下：

时刻0时，由于水池中水量大于对第1时段（即0时刻到1时刻）的水需求量预测值，所以第1时段的抽水策略不需要调整；同样对第2时段（即1时刻到2时刻）的水需求量预测值可见，第2时段的抽水策略也无需调整；

如此下去，直到时刻9时，水池中水量小于第10时段(即9时刻到10时刻)的水需求量预测值。这时，假设第10时段抽水，水池中水量加上第10时段的抽水量大于对第10时段(即9时刻到10时刻)的水需求量预测值，所以第10时段的抽水策略需要调整，即将在第10时段改为抽水，相应的抽水费用增加到55.485。

从图中可以看出经过局部调整后的预测值都能满足用水需求。

表3 第14天的抽水费用及抽水情况

从表3中可以看出，整体优化加上局部调整之后，既满足了用水需求，同时也减少了抽水费用且制定了相应的抽水方案。

6 结束语

本文通过数学建模的思想对楼宇蓄水池每天用户需求量进行整体规划，制定的抽水方案在一个地方用水相对稳定的情况下是适用的。而对未来需求量的预测方法有很多，如指数平滑、灰色预测等等，本文只是采用了其中一种，但无论采用哪一种方法预测都有可能达不到用户需求，所以制定良好的局部调整策略对制定未来抽水方案有较大的影响，相对传统的抽水方式在节约水、电以及制定抽水方案等方面具有明显的优势。本文给出的优化方案有利于合理使用电力资源，使得费用最小化，只要将文中模型、算法程序化，并结合硬件控制器，即可实现对蓄水池的智能控制与优化。

注：其中红色为对第14天的预测值，蓝色为第14天的真实值。

[1]欧阳春光，许丽娟，分段电费计价对家电的影响[J]，家用电器，2001年第7期 21页.

[2]张文昭，包本刚，潘海军，陈爱武，楼宇水塔水位检测与抽水自动控制系统[J]，湖南科技学院学报，2009年第8期第30卷48页.

[3]黄伟锋，李震，智能化楼宇自动蓄水控制系统[J]，机电工程技术，2007 年第10期第36卷55页.

[4]李静锋，陈义厚，水塔自动抽水装置的设计与研究[J]，大众科技，2008年第1期第116页.

[5]司夺奎，数学建模算法与程序[M]，海洋航空工程学院.

[6]卓金武，Matlab在数学建模中的应用[M]，北京航空航天大学出版社，2011-4-1.