一个数值求积公式的渐进性质＊

龙爱芳 胡军浩

（中南民族大学数学与统计学学院 武汉 430074）

0 引 言

随着科学技术和计算机技术的飞速发展，计算方法也显得日益重要，在计算方法中占有重要地位的数值积分也在飞速发展.而数值积分公式要提高精度的基础是积分中值定理中间点的渐近性质.文献［1－2］给出积分中值定理中间点的渐近形态的2个结论，文献［3］给出曲线积分中值定理中间点的一个一般性的结果，文献［4－6］根据积分中值定理中间点的渐近形态得到数值积分公式的渐近性.对于数值积分公式，最好是精度要高，同时计算也要简单，这是一个矛盾的事情.要想得到高精度的数值积分公式，必须提供导数，精度越高需提供的导数的阶数就越高，如果被积函数比较复杂，计算导数是非常麻烦的.有没有精度相对较高，而不需要计算导数的数值积分公式？答案是肯定的：Simpson公式只需要提供3 个节点的函数值，有3次代数精度，误差量级为O（h5）；复化Simpson公式只需计算节点处的函数值，误差量级为O（h4）.本文构造的数值积分公式同样可以不用计算导数值，只需要计算节点处的函数值，计算量与复化Simpson 相当，但它却有比复化Simpson更高的精度，误差量级为O（h6），和文献［5－6］相比具有形式更简单，计算量更小等优点.下面介绍本文的数值求积公式.

1 数值求积公式

1.1 插值多项式的构造

构造满足插值条件：

的次数不超过4的Hermite插值多项式H（x），其中xk，xk＋1，xk＋2为3个等距节点，即xk＋1＝xk＋h，xk＋2＝xk＋2h，则H（x）可以表示为

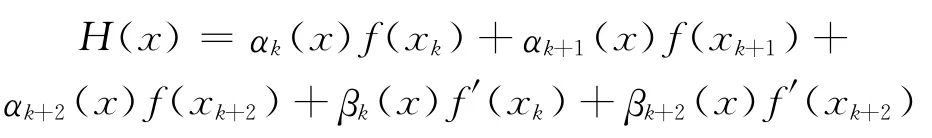
其中：插值基函数αk（x），αk＋1（x），αk＋2（x），βk（x），βk＋1（x）分别具有如下的表达式：

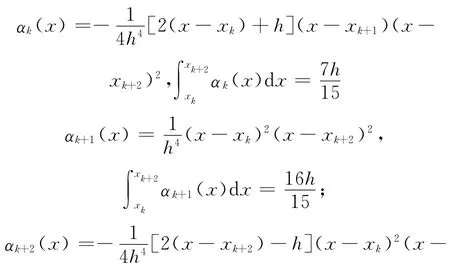
至此，满足插值条件的Hermite插值多项式构造完毕，余项表达式为

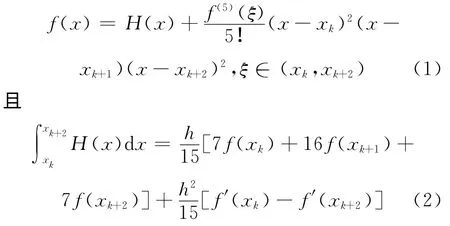
1.2 数值求积公式的构造

式（1）两边求积分并应用式（2）进一步分析得：

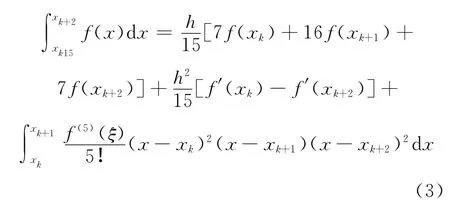
在式（3）中令xk＝a 可得本文的第一个数值求积公式

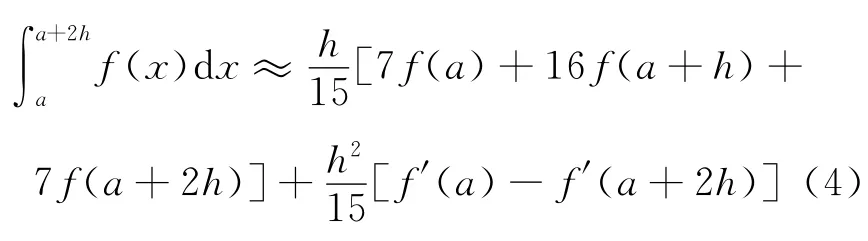
则至少具有5次代数精度且误差量级为O（h7）的数值积分公式构造完毕.并有式（3）得到如下积分中值定理：

定理1 如果f（x）在区间［a，a＋2h］上有直到6阶连续导数，则存在ξ∈（a，a＋2h），成立

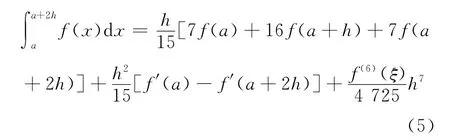
下面研究式（5）中间点ξ的渐进性.

假设有形如

的数值求积公式，设η＝a＋λh，要使式（6）的代数精度尽可能高，下面确定λ的值.

在式（6）中，显然当f（x）＝1，x，x2，x3，x4，x5时准确成立，当f（x）＝x6时，

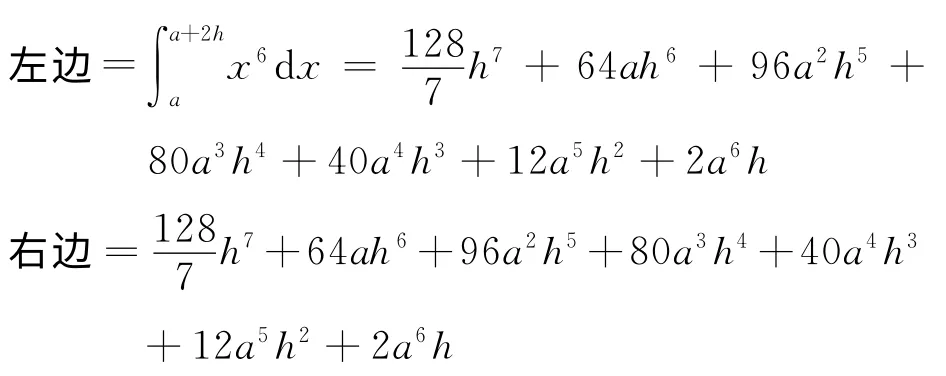
左边＝右边，即无论η取（a，a＋2h）中的任何值，数值求积式（6）均有至少6次代数精度.

式（6）中，当f（x）＝x7时

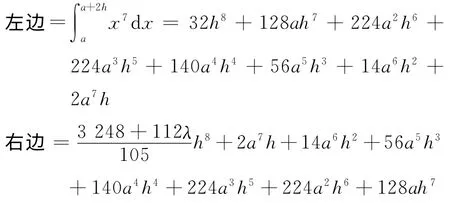
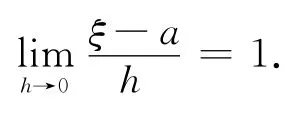
于是得到了本文的至少具有7次代数精度的第二个求积公式

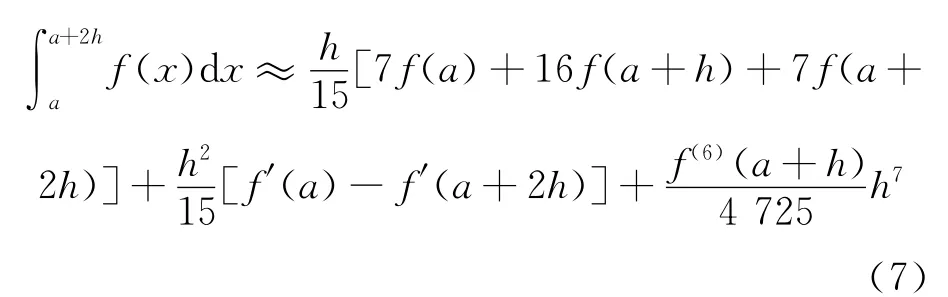
下面研究式（7）的误差量级.

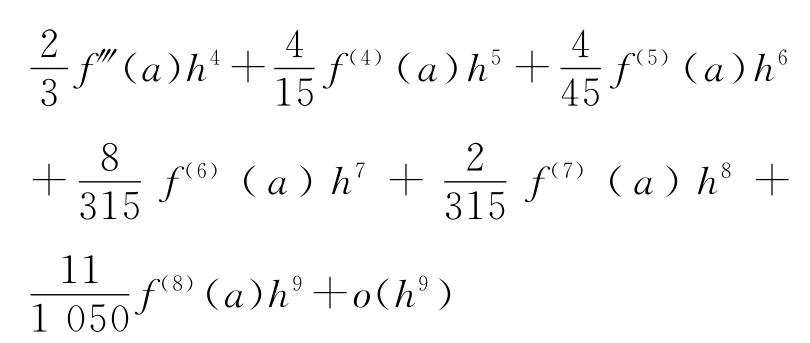
比较左边和右边知数值求积式（7）的误差量级为O（h9）.

定理2 如果f（x）在［a，a＋2h］上有直到8阶连续导数，则有

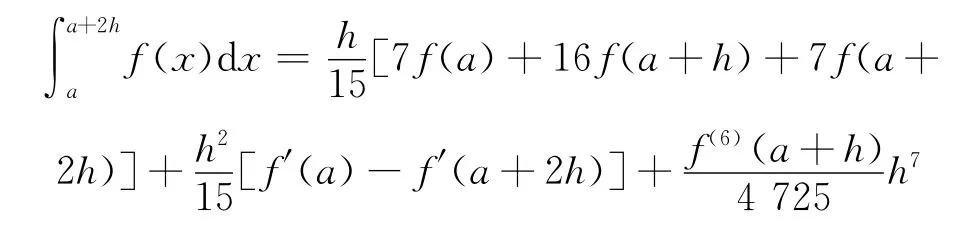
1.3 求积公式的进一步改进

由于本文得到的两个数值求积公式虽然精度高，但是必须计算节点处的一阶导数和高阶导数，为了克服这一缺点，应用式（5）复化求积得：

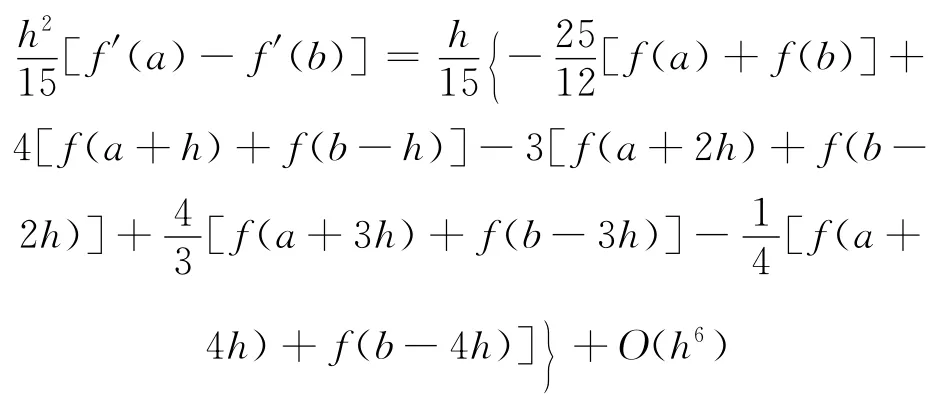
故得到本文的第三个数值求积公式：

它只需要计算节点处的函数值，不用计算任何导数值，计算量与复化Simpson公式相当，但精度却得到很大的提高，误差量级提高了两次.

定理3 如果f（x）在［a，b］上有直到6阶连续导数，则有

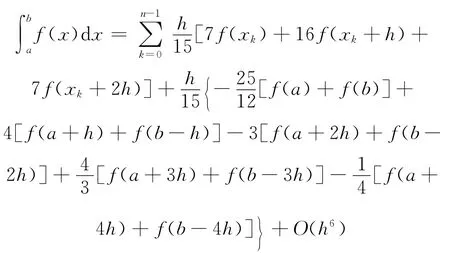
1.4 数值试验

表1 三个数值求积公式的计算结果

表2 复化Simpson公式和本文复化公式（9）的计算结果

2 结 论

1）由本文的积分中值定理

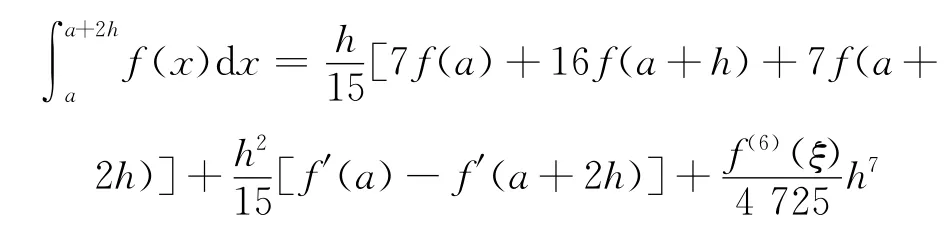
给出数值求积公式

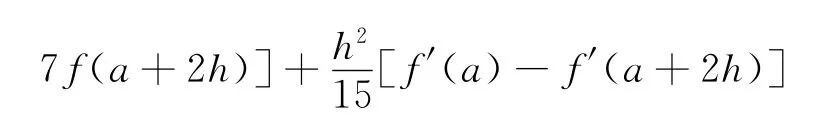
2）据积分中值定理中间点ξ的渐近性态，得到具有更高精度（7次）的数值求积公式

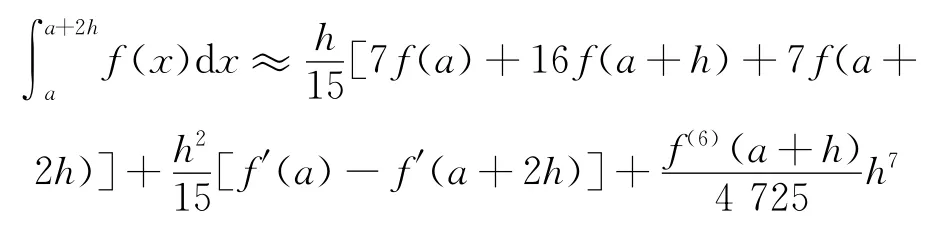
3）为了避免导数计算，应用复化求积，给出本文的第三个数值求积公式

从计算结果可以看出，本文给出的3个数值求积公式均非常有效.

［1］王福良，杨彩萍.积分中值定理中间点渐近形态的研究［J］.天津师范大学学报：自然科学版，2002，22（2）：38－40.

［2］赵奎奇.积分中值定理中值研究的进一步结果［J］.数学的实践与认识，2006，36（4）：292－295.

［3］赵益坤.关于曲线积分中值定理中间点的一个一般性的结果［J］.大学数学，2007，23（1）：166－169.

［4］YANG Caiping.A result on the mean value theorem for integrals［J］.Journal of Mathematics for Technology，2001，17（4）：91－92.

［5］刘彬清.一类高斯求积公式的极限性质［J］.工程数学学报，2003，20（4）：137－139.

［6］刘彬清.关于一些求积公式的渐近性［J］.应用数学与计算数学学报，2002（2）：83－87.