基于拟T－S模糊模型的网络化控制系统的卡尔曼滤波器设计＊

章 红方华京 任先平

（华中科技大学控制系1） 武汉 430074） （江汉大学物理与信息工程学院2） 武汉 430056）

0 引 言

考虑具有噪声的线性定常离散系统用以下状态空间模型来描述［1－2］：

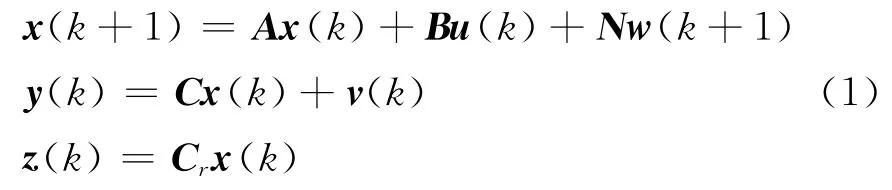
式中：x（k）∈Rn×1，u（k）∈Rm×1，y（k）∈Rl×1，z（k）∈Rq×1分别为系统状态向量、输入向量、传感器测量输出及系统实际输出向量；w（k＋1）和v（k）分别表示系统扰动和测量噪声，它们是不相关的、具有零均值的高斯白噪声，在采样间隔内，w（k）和v（k）均为常值，其统计特性为

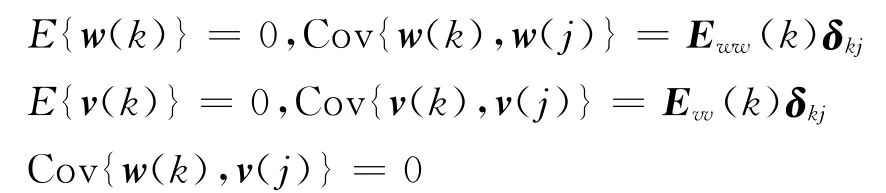
A∈Rn×n，B∈Rn×m，C∈Rl×n和Cr∈Rq×n分别为系统的状态矩阵、输入矩阵、传感器测量矩和输出矩阵，Eww（k）∈Rn×n，Evv（k）∈Rl×l分别为w（k）和v（k）的方差矩阵.

状态向量的初始值x（0）的统计特性给定为

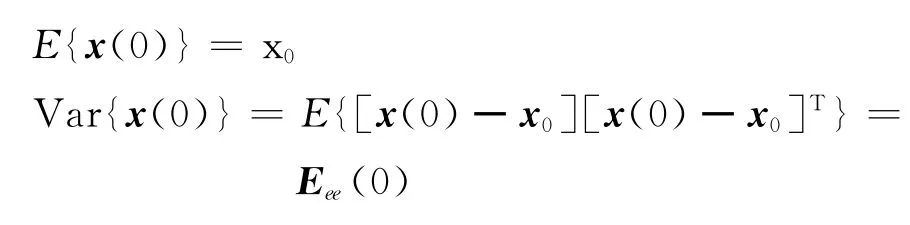
1 NCS系统模型

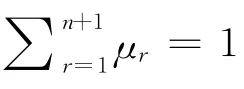
利用网络时延作为模糊变量，时延出现的概率作为隶属度函数，构造基于T－S模糊模型的拟T－S模型（quasi T－S fuzzy model，QTS）［3－6］.

根据时延的特性，将线性控制系统分为n＋1个子系统，前面的n 个子系统是没有数据包丢失的情况，当时延τ＞nTs时，假设出现丢包情况.

当时延τ＞nTs时，根据丢失的信息不同分别讨论：（1）若τca＞nTs，则控制器传递给执行机构的控制信息丢失，此时相当于一个开环系统；（2）若τsc＞nTs，则传感器传递给控制器的状态信息丢失，可以利用卡尔曼滤波器进行状态滤波和预估控制.

因此，构造n＋1个模糊子系统的系统模型，其中第r个模糊子系统分为2部分构造：

第一部分

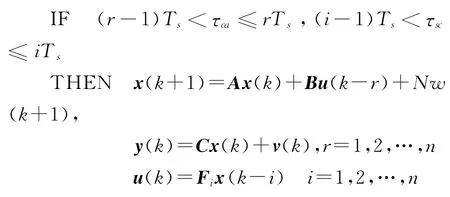
第二部分

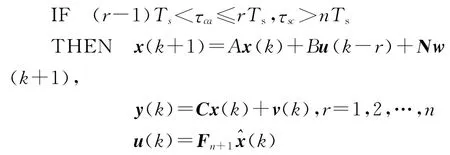
第n＋1个子系统的模型为

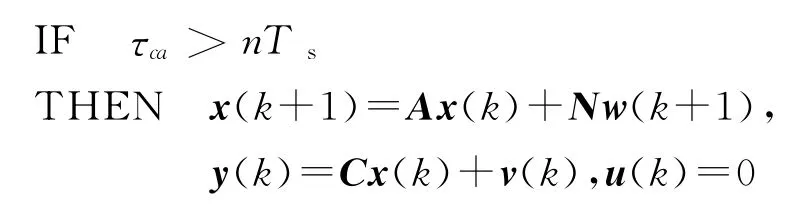
经模糊融合后得到NCS的模型为

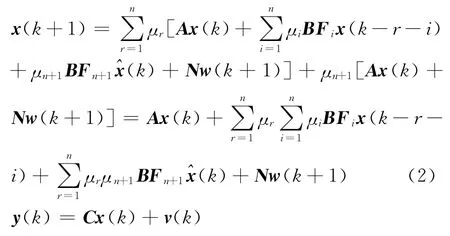
2 基于QTS模型的NCS状态估计器的设计

由于每一个子系统的系统矩阵、输入矩阵和输出矩阵都是相同，所以在每个采样时刻，子系统的增益矩阵、预测误差方差阵和滤波方差阵具有相同的形式，针对NCS系统出现丢包的情况，构造每个子系统的卡尔曼滤波器THEN

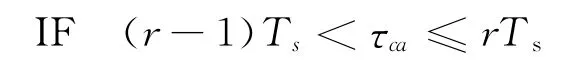
式中：Kr（k＋1）为待优化的增益矩阵算子.

3）增益矩阵

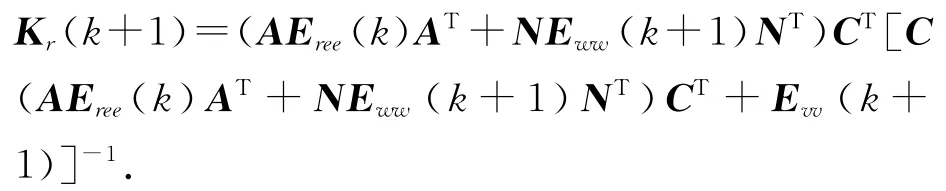
4）预测误差方差阵

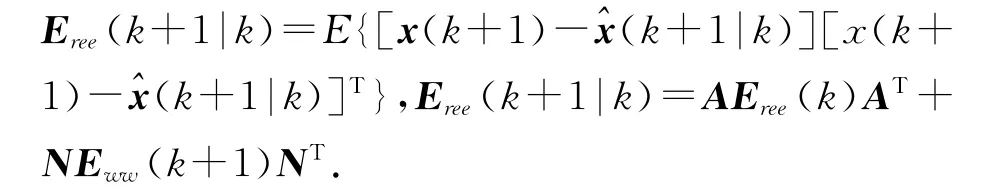
5）滤波误差方差阵

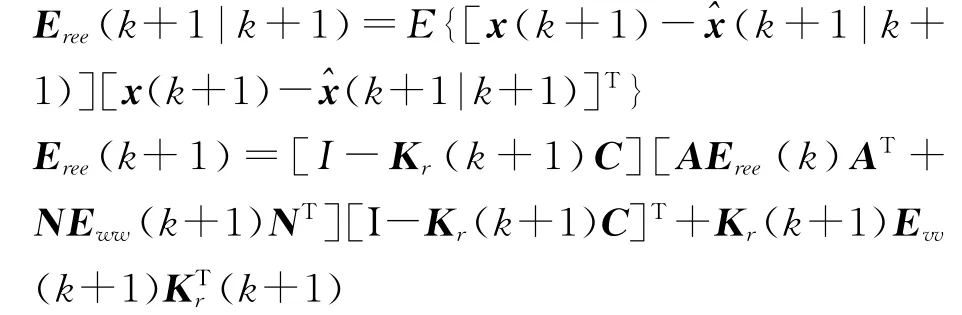
即：

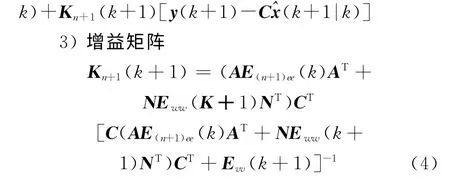
4）预测误差方差阵 E（n＋1）ee（k＋1｜k）＝AE（n＋1）ee（k）AT＋NEww（k＋1）NT

5）滤波误差方差阵

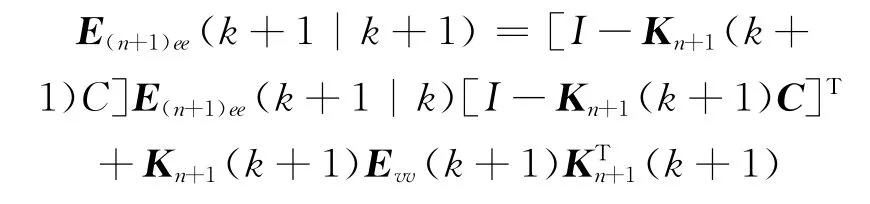
则经过模糊融合后系统的全局状态估计：

1）状态预估方程

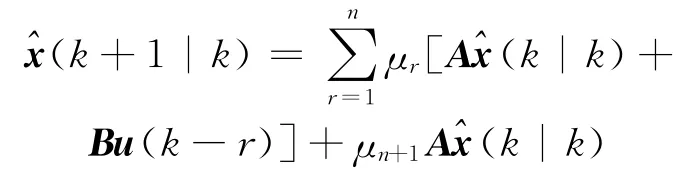
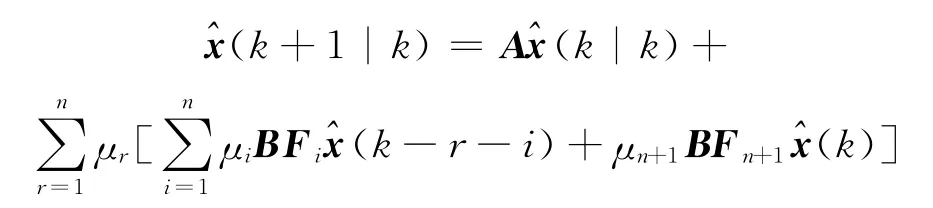
2）估计校正方程

3 模糊卡尔曼滤波器的数字仿真

以一个二级倒立摆系统为例进行分析.倒立摆系统的状态空间描述如下.

根据二级倒立摆系统运动的特点，极点配置应满足鞍点特性，所以取满足要求的极点为

假设网络控制系统的采样周期T＝0.05s，系统的时延分布特性满足本文开始的假设，当延迟时间τ＞0.15s时，认为系统出现丢包.系统时延和丢包出现的概率分布满足μ＝｛0.3，0.5，0.1，0.1｝.其中：μ1，μ2，μ3 为系统传输出现不同时延的概率，即n＝3，μ4 为系统传输出现丢包的概率.由于，各个子系统的系统矩阵、输入矩阵和连接矩阵都没有发生变化，所以根据极点配置的要求取状态反馈矩阵

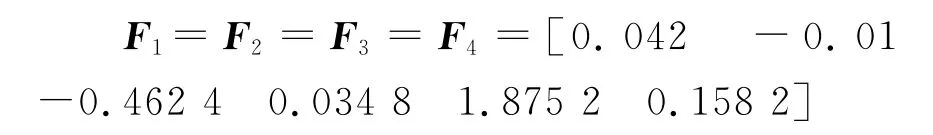
利用MATLAB仿真得到滤波器与系统输出之间的波形关系，见图1.

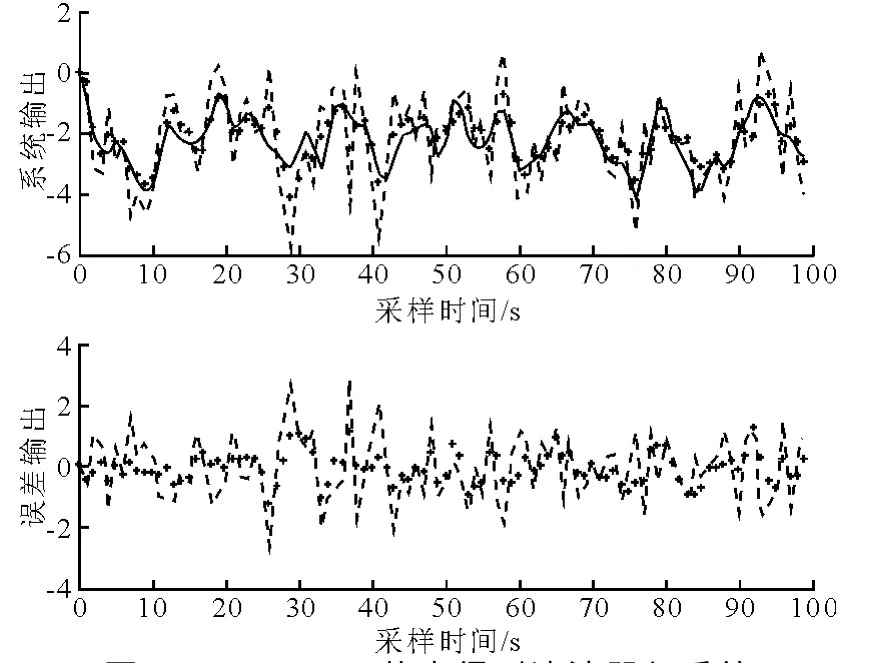
图1 MATLAB仿真得到滤波器与系统输出之间的波形关系图

在输出波形中，实线给出的是系统期望输出的波形，虚线表示的是系统受到噪声影响情况下的输出波形，用点点表示的波形经过滤波器的输出波形，可见所设计的卡尔曼滤波器可以滤去噪声的影响，更接近系统的实际输出.通过第二组的误差波形，可以更清楚地看出滤波特性，虚线反映的是实际输出和理想输出之间的误差，点线反映的是滤波器输出与理想输出之间的误差，很显然滤波器可以很好地抑制噪声对系统的干扰.

通过上述基于QTS模型构建的NCS系统卡尔曼滤波器可以很好地实现对噪声的抑制作用，以此为基础可以进一步展开对NCS系统故障诊断和容错技术的研究.亦可以将滤波器的应用推广到更广泛的领域.

［1］王志贤.最优状态估计与系统辨识［M］.西安：西北工业大学出版社，2004.

［2］张贤达.现代信号处理［M］.2版.北京：清华大学出版社，2002.

［3］FANG Huajing，ZHANG Hong，FANG Yiwei，et al.Quasi T－S fuzzy models and stable controllers for networked control systems［C］∥Proceedings of the World Congress on Intelligent Control and Automation，Dalian：IEEE，2006：220－223.

［4］FANG Huajing，YANG Fang，ZHENG Ying，et al.Fuzzy modeling and fault detection for networked control systems［C］∥6th IFAC Symposium on Fault Detection， Supervision and Safty of Technical Processes，Beijing：IEEE，2006：1091－1096.

［5］章 红，方华京，任先平.基于拟T－S模糊模型的网络化控制系统稳定性分析［J］.武汉理工大学学报：交通工程版，2012，36（1）：203－206，210.

［6］章 红，方华京，任先平.基于拟T－S模糊模型的网络化控制系统鲁棒性分析［J］.华中科技大学学报：自然科学版，2011，39（8）：108－113.