基于有限元的锁环静态分析与结构优化*

李 盼，薛晓宁

(广东海洋大学工程学院，广东 湛江 524088)

1 前言

碟式分离机工作时转鼓高速旋转，利用离心力实现物料的连续高效分离，如图1所示乳胶分离机转鼓由100多个零件组成，整个转鼓依靠锁环螺纹将转鼓底、转鼓顶等连接成一体，在影响转鼓及整机安全性的3个零部件转鼓底、转鼓盖和锁环中，锁环最为薄弱［1］，发生安全事故后造成的危害性最大，在高速状态下其受载状态十分复杂，对其受载状态进行研究十分必要，尚未见到国外锁环强度分析方面的研究的报道，经典弹性力学理论不能有效解决复杂结构应力分析，本文利用有限元法对锁环结构进行有限元分析。

图1 碟式分离机转鼓剖视图

2 锁环结构静态应力有限元分析

2.1 确定锁环结构几何参数

碟式分离机转鼓主要由转鼓底、碟片组、碟片压盖、转鼓盖、喇叭管、锁环等零部件组成。本文将利用有限元对锁环进行结构应力分析与参数优化［4］，锁环结构如图2所示，相关几何参数如下:d1=33.5 mm，d4=15.5 mm，d5=57.5，d6=14 mm，d7=94.5 mm，d8=221 mm;螺纹为矩形单线螺纹。

图2 锁环结构二维图

2.2 建立三维实体模型

锁环为轴对称模型，利用CAD建模软件建立锁环实体模型，为减少计算时间，提高分析效率，取结构1/4分析，其实体模型如图3(a)所示。

2.3 建立有限元模型

定义材料属性:锁环材料为35 CrMo，其弹性模量(杨氏模量)为 E=2.06 GPa，泊松比为 μ =0.3，密度为ρ=7900 kg/m3，屈服强度为σs=835 MPa，抗拉强度为σb=985 MPa。

图3 锁环计算模型

网格划分:为了取得较规则网格效果，选择扫掠网格划分方式，手动设置左右两个对称端面作为扫掠源面与目标面，整体网格单元大小为2 mm，对上端结构和螺纹区域做网格细化处理，设置网格单元大小为0.5 mm，得到网格划分单元数为147433，节点数为95194，得到的锁环网格划分模型如图3(b)所示。

施加位移约束:由于选取锁环模型的1/4进行分析，对左右两端面施加无摩擦对称边界约束，限制结构沿X、Y、Z轴移动自由度和绕X、Y轴转动自由度。

施加载荷约束:锁环加工状态受力十分复杂，对结构受力进行必要简化处理。

(1)锁环自重离心力F1

以角加速度ω形式施加于绕轴向方向旋转。

(2)转鼓顶盖对锁环作用力简化为均布面载荷［2］，施加于锁环上端与顶盖接触面位置。

(3)转鼓装配产生的预紧力F0采用ANSYS预紧力模块施加。

(4)转鼓内腔胶乳产生的液体离心分布压力［2］为F2:

式中:ρ为胶乳物料液体密度;r0为转鼓内胶乳液体自由表明半径;转鼓筒体与锁环接触位置的作用力主要由胶乳液体离心压力产生，利用ANSYS自带Mechanical APDL命令流施加于锁环螺纹截面处。

2.4 有限元分析计算结果

进入Solution分析进行求解，得到锁环静力分析计算［3］结果如图4所示。

图4 锁环应力与变形云图

分析图4可知:在锁环退刀槽、螺纹牙根位置有较大的应力存在，其中锁环下端最后一扣螺纹旋入位置应力水平最高，最大等效应力值为554.12 MPa。位于锁环上端位置，几何变形最为明显，其中最大几何变形量为0.28713 mm。这相对于35 CrMo材料屈服极限还有较大的优化空间。

3 锁环结构多目标驱动优化

3.1 基于AWE结构优化

优化设计［4］目的是寻求最优设计方案，在提高结构承载能力的同时减轻重量，其数学模型的一般表达式:

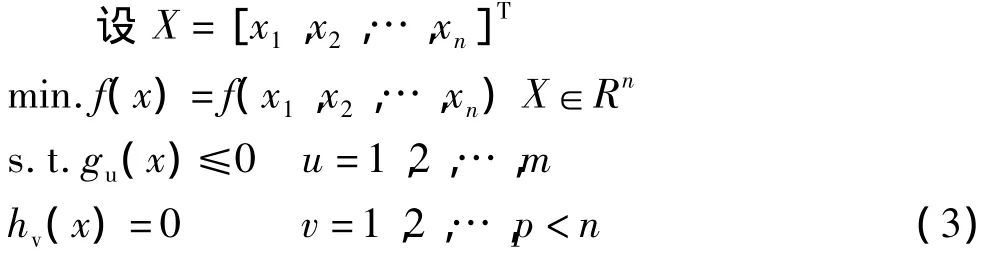
应用Workbench进行结构多目标优化时，通常先定义目标函数、设计变量及状态变量等参数［5］。

目标函数设置:从锁环应力分析结果可知，最大等效应力值偏大。在结构目标函数设置过程中，必须保证结构安全，并尽可能减轻质量、减少应力集中及总体位移变形。综合考虑，锁环结构目标函数按以下设置:保证锁环结构最大等效应力值尽可能小，优先级设为最高;在满足结构安全的条件下质量取最小值，优先级次之;最大几何变形量尽可能小，优先级别最低。

设计变量设置:从锁环应力分析结果可知，应力主要集中于靠近螺纹旋入位置，与顶盖接触位置的几何变形明显，综合这两个因素，锁环设计变量如表1设置，各设计变量的变化范围以软件默认的优化前尺寸±10%进行约束。

表1 设计变量与约束条件

状态变量设置:将锁环最大等效应力值和质量分别作为状态变量，为保证强度锁环的最大等效应力值必须小于许用应力值835 MPa，设计时使质量减少。

3.2 输入参数敏感性分析

灵敏度可以显示设计点对输出参数的敏感度，通过分析设计变量或结构参数的变化对结构特性影响的敏感度，为结构优化分析提供依据，确定最优方案，有效避免结构设计中的盲目性，提高设计效率，减少材料消耗，降低生产成本。图5为锁环参数设计点灵敏度分布图。

由图5可知:d1、d7对锁环结构优化设计目标函数的敏感度影响因子较大，在进行锁环响应分析时，主要考虑参数d1与d7对目标函数的影响。

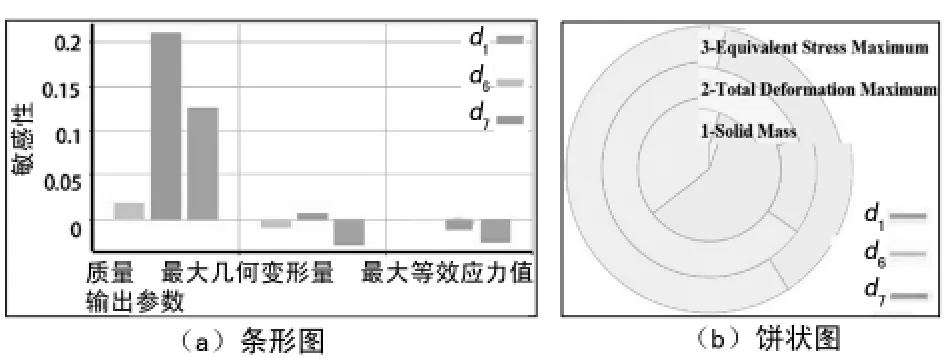
图5 锁环设计变量与目标函数灵敏度分布图

3.3 优化参数响应图

基于AWE综合响应分析，可直观观察输入参数对优化计算结果的影响，通过响应曲线或响应曲面的形式反映输入参数与输出数值之间的相互关系，即在任何响应点处可以观察输出参数的灵敏度，观察一个输出参数如何随着一个或多个输入参数的变化而变化。在多目标优化设计［6］过程中，由多个输入参数组成的优化程序，AWE平台也可以很方便地根据需要查看某个或某几个输入参数对优化结果的影响。

图6 设计变量与锁环结构目标函数二维响应曲线变化关系

锁环响应分析:通过敏感性分析，实验设计法中的设计点与输出参数关系曲线可知，d1、d7比d6对锁环物理特性影响相对敏感，因此主要考虑锁环设计变量几何参数d1、d7与目标函数之间的关系，如图6所示为锁环设计变量与目标函数之间的曲线关系。

由图6可知:d1越大，最大等效应力值越小，最大几何变形量越大，质量增加;d7越大，最大等效应力值越大，最大几何变形量呈先变大后变小的规律变化，质量增加。

为了更清楚了解设计变量参数对目标函数的影响，如图7所示，以参数d1、d7作为空间响应曲面的两个坐标，另一坐标设置为目标函数值，得到锁环设计变量d1、d7与各目标函数之间的响应曲面关系。

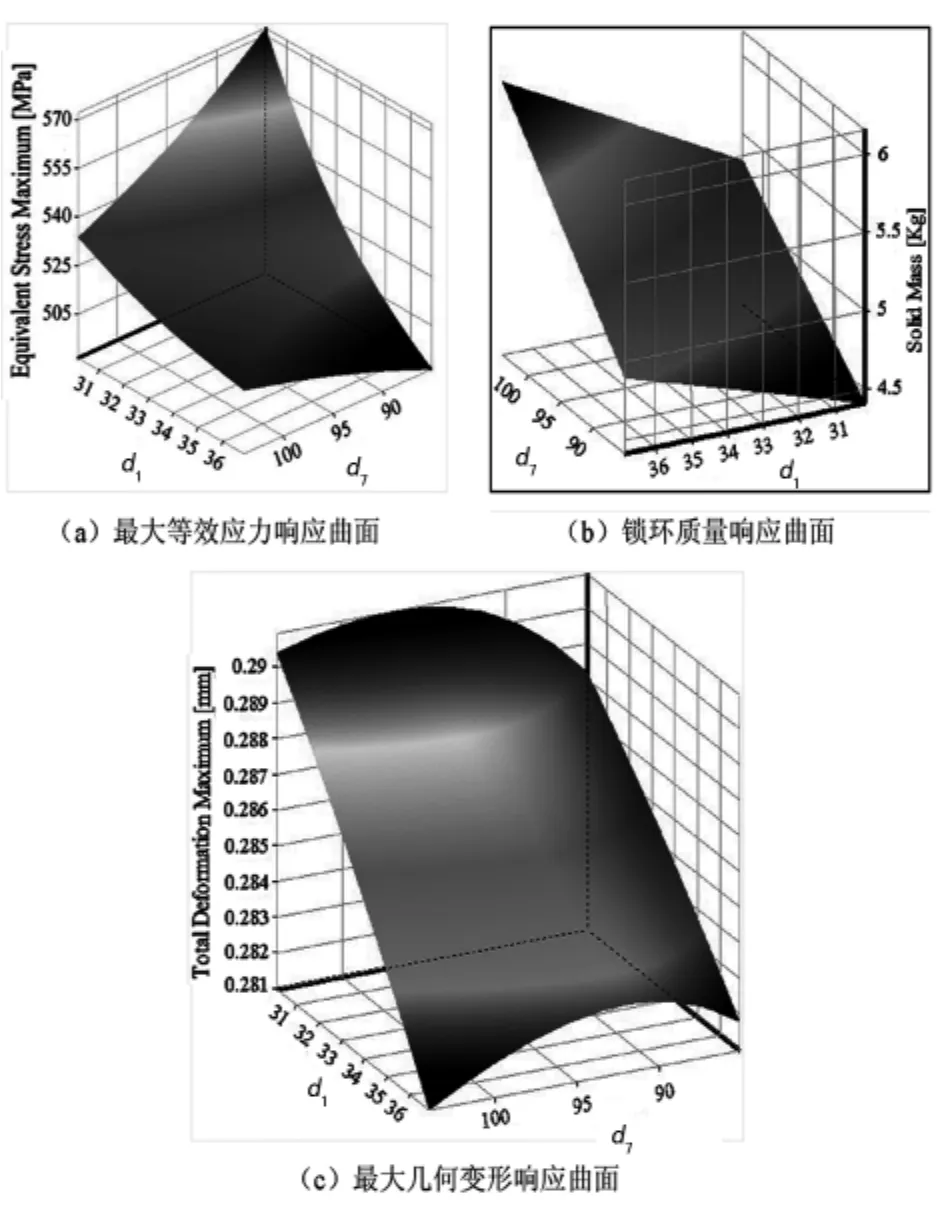
图7 三维响应面

3.4 确定最优解

对锁环进行优化时，通过目标驱动优化分析获得候选设计点，优化求解之后，得到的三组最优解候选设计点如表2所列。

综合考虑最大等效应力、锁环质量及最大几何变形量三个因素，最终确定选择候选设计点A方案为最优设计方案，将方案A插入设计点，更新几何参数后得到优化模型，重新进行求解，得到优化后设计结果如表3所示，并与优化前的分析数据进行对比。

表3可知:设计变量参数d1、d7相对优化前略有增大，d6减小，最大等效应力减小幅度60.96 MPa，降低11%，质量较优化前减小了 0.6504 kg，下降12.5%，几何变形也略有降低，受载状态得到改善，材料消耗减少。因此结构参数优化设计后，在结构几何尺寸及质量减少，强度得到提高。

表2 锁环优化候选设计点

表3 锁环优化设计前后各参数对照表

4 结语

建立了碟式分离机转鼓锁环的三维实体模型，在ANSYS Workbench环境里进行了有限元结构静力学分析，得到锁环应力与变形分布云图。根据分析结果，确定了优化设计变量与目标函数，进行锁环参数优化设计，通过优化分析，锁环质量、最大等效应力、最大几何变形量均有所降低。本文分析方法及结论对分离机设计及强度优化具有借鉴价值。

［1］韩 捷，梁利华.碟式分离机转鼓锁环的有限元应力分析［J］.浙江:浙江工业大学学报，2002，30(5):460 －463.

［2］孙启才，金鼎五.离心机原理结构与设计计算［M］.北京:机械工业出版社，1987.

［3］宋向辉，王 红，商跃进.动车转向架构架强度分析［J］.机械研究与应用，2012(2):1－3.

［4］查太东，杨 萍.基于ANSYS Workbench的固定支架优化设计［J］.煤矿机械，2012，33(2):28 －30.

［5］周万春，王启佳，孙 维，等.基于ANSYS Workbench的刮板输送机中部槽优化设计［J］.煤矿机械，2012，33(4):8 －9.

［6］赵 强，崔建昆，叶 芯.碟式分离机转鼓体应力分析与优化设计［J］.机械设计与制造，2007(1):21－23.