雷达辐射源特征参数提取算法复杂度分析

徐 璟，何明浩，陈昌孝，周 琳

(1.空军预警学院，武汉 430019；2.电子信息控制重点实验室，成都 610036；3.海军东海舰队司令部，浙江宁波 315000)

0 引 言

随着现代战争的发展，新体制雷达不断出现，雷达信号形式日益复杂，利用常规参数已经不能对雷达辐射源进行准确的分选和识别，为了更有效的对雷达辐射源进行分选和识别，人们对雷达信号脉内特征进行分析和提取。

脉内特征是雷达辐射源信号最具特色的参数之一，虽然当前的一些雷达辐射源信号的常规参数变化丰富，但其脉内特征参数却具有一定的稳定性［1］。目前，一系列的脉内有意调制特征参数被提取，如熵值［2，3］、小波包特征［3～5］、复杂度特征［6］等。这些特征参数都具备对雷达辐射源进行分选、识别的功能，而且都具有较高的识别率和参数稳定性，但就特征提取算法时间复杂度而言，目前研究人员只是给出运行一次或多次算法所需的时间或对算法运行的阶数进行分析，由于计算机性能不同，所以算法运算时间也不尽相同，无法对特征提取算法复杂性做出准确的评价。为此，从算法设计和数据结构入手，通过计算算法主要步骤每种运算的运算次数，分析特征提取算法的时间复杂度，推导出每种特征提取算法时间复杂度的计算公式，对特征提取算法进行评价。最后通过对五种特征提取算法进行计算机仿真，得出每种算法运行50 次的平均时间，验证本文分析的正确性。

1 五种特征提取算法

1.1 熵特征(En)

熵特征主要用来表示信号的不确定程度，用于雷达辐射源信号分选识别的熵特征主要有两种，近似熵(ApEn)和范数熵(NoEn)，而范数熵能定量描述信号的能量分布情况，所以在频谱形状不同，能量分布和集中程度不同的雷达辐射源信号特征提取中应用较广泛。范数熵特征的提取过程如下。

Step 1:对雷达信号进行预处理，即将信号序列由时域变换到频域，并对信号能量进行归一化处理，得到信号的中心频率和有效带宽。处理后的信号为{f(i)，i=1，2，…，N}。

Step 2:将处理后的信号，计算范数熵的值

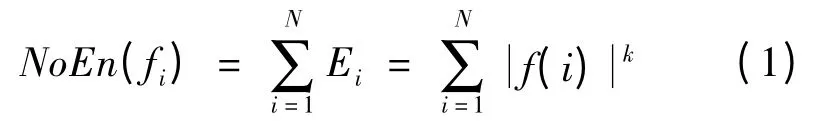
在Step 1 过程中对信号进行了归一化处理，{f(i)，i=1，2，…，N}的值在［0，1］之间，故信号能量越集中，范数熵值越大;反之，信号能量越分散，范数熵值越小。所以，范数熵值能反映信号能量分布的总体情况。

1.2 相像系数特征(CR)

采用不同脉内调制方式的雷达辐射源脉冲信号其频谱形状也是不同的，而且频谱形状的变化蕴含着脉冲信号的频率、相位和幅度的变化信息。因此，相像系数能对雷达辐射源信号的频谱形状进行有效刻画，是一种能有效区分不同脉内调制方式信号的特征参数［7］。相像系数受噪声影响较小，当信噪比大于5 dB 时，相像系数的值即趋于稳定。因此，利用相像系数可以将不同调制类型的信号有效分类，在常规参数的基础上补充相像系数是行之有效的方法。提取相像系数的具体步骤如下。

Step 1:对雷达信号进行预处理，即将信号序列由时域变换到频域，并对信号能量进行归一化处理，得到信号的中心频率和有效带宽。处理后的信号为{f(i)，i=1，2，…，N}。

Step 2:计算矩形信号序列{U(k)}和{f(i)}的相像系数，计算公式为

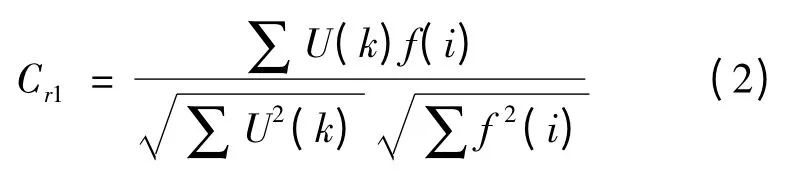
Step 3:计算三角信号序列{T(k)}和{f(i)}的相像系数，计算公式为

Step 4:将Cr1和Cr2组成联合特征向量集，称为相像系数CR= [ Cr1，Cr2]。

1.3 模糊函数特征(AF)

模糊函数是对雷达辐射源信号进行分析研究和波形设计的有效工具［8］，其完全取决于雷达辐射源所发射的信号波形。由于模糊函数提供了对信号结构信息较为完整的描述，因此利用模糊函数能挖掘出反映不同信号结构信息之间差异的特征参数。但提取的模糊函数二维特征图维数为800，极大的影响分选速度，因此，在提取模糊函数二维特征图后，利用小波包对其进行分解，得到不同信号序列间的差异。提取模糊函数特征的算法步骤如下。

Step 1:求取接收信号的模糊函数，公式为

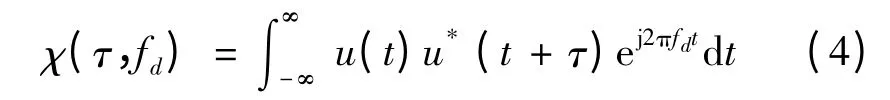
式中，u(t)为信号的复包络;τ 为延时;fd为多普勒频率差。

Step 2:将模糊函数简化为二维特征图。

简化方法为选择沿X 轴作平行于YOZ 平面的等间隔截面，得到M 个截面，取M 个截面的最大值作为特征向量，由此得到二维特征图。

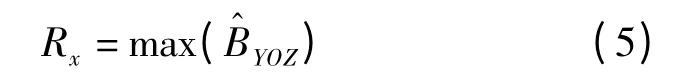
Step 3:求取二维特征图的小波包特征Wpt。

这里对二维特征图进行3 层小波包分解，第3 层共有8 个频带，分别包含着8 个频带的特征信息。用S3j(j=1，2，…，8)表示重构信号，则总信号可以表示为

S=S31+S32+S33+S34+S35+S36+S37+S38(6)

则可得到S3j的能量E3j(j=1，2，…，8)，

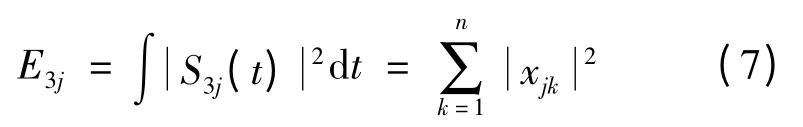
对其进行归一化处理可得到Wpt。

Step 4:将Wpt2和Wpt5作为分选、识别雷达辐射源信号的特征参数。

Wpt2和Wpt5在八维Wpt中具有最佳的类间分离度，因此最终选择其作为分选、识别不同雷达辐射源信号的新特征参数。

1.4 复杂度特征(C)

雷达辐射源信号波形的复杂性能反映信号的调制方式，通常可选择关联维数、盒维数、信息维数和Lempel-Ziv 四种复杂度特征来区分雷达辐射源信号。复杂度特征受信噪比的影响较小，尤其是盒维数和信息维数，为此文献［9］将盒维数应用到通信信号的识别中，但是直接从时域波形上提取信号的盒维数只能反映信号序列的几何尺度信息，若要全面的反映信号序列的复杂度，还需对信号的稀疏性进行提取，将盒维数和稀疏性作为复杂度特征进行提取［10］。其特征提取算法步骤如下。

Step 1:对雷达信号进行预处理，即将信号序列由时域变换到频域，并对信号能量进行归一化处理，得到信号的中心频率和有效带宽。处理后的信号为{f(i)，i=1，2，…，N}。

Step 2:求取预处理后信号序列的盒维数Df，求取公式为

Step 3:求取预处理后信号序列的稀疏性μ，求取公式为

设GN=g1，g2，…，gN为一维(0，1)空间中的一个序列，该序列中包含M 个“1”元素。为了能够描述在序列GN中不同位置处的疏密特性，构造一长度为N0的窗函数，使其在序列GN上由左至右滑动，第i 个窗口内包含的“1”元素为Mi个，则该窗口内的平均稀疏性可定义为μ

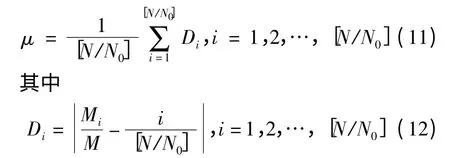
Step 4:将Df和μ 作为雷达辐射源信号分选、识别所用的频域复杂度特征参数。

1.5 双谱特征(BI)

经预处理后的雷达辐射源信号所含的噪声主要包括各种杂波、接收系统热噪声等，而这些噪声均趋于高斯分布。文献［11］证明了高阶谱作为时间序列分析的工具可以有效抑制高斯噪声的影响。因此，对接收到的雷达辐射源信号首先提取其双谱，以达到有效抑制高斯噪声的目的。但是，双谱幅度谱为三维特征，具有很高的维数，不便于运用机器进行分选处理，因此需进一步简化为二维特征，并提取其相像系数，将双谱二维特征相像系数作为新的特征参数。其提取步骤如下。

Step 1:提取接收信号的双谱幅度谱。

将数据{x(0)，x(1)，…x(N－1)}分成K 段，每段M 个样本，即N=KM，这里允许两段相邻数据间的重叠;将所给数据x(0)，x(1)，…，x(N －1)的双谱估计以K 段双谱估计的平均值给出，即

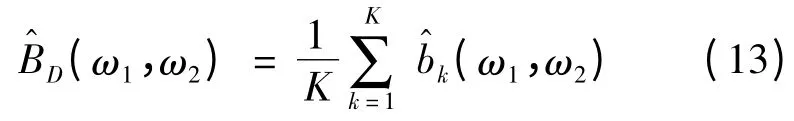
Step 2:将双谱幅度谱简化为二维特征。

简化方法和模糊函数二维特征图的简化方法一样。

Step 3:分别求取双谱二维特征的相像系数。

Step 4:将双谱二维特征相像系数作为雷达辐射源信号分选、识别的新特征参数。

2 算法复杂度概念

在已验证算法正确性的前提下，算法复杂度的高低主要体现在执行该算法所需的计算机资源的多少上，所需要的资源越多，该算法的复杂度越高;反之，所需要的资源越少，该算法的复杂度越低。计算机的资源，最重要的是时间资源和空间资源。因此，复杂度可分为时间复杂度和空间复杂度。由于时间复杂度与空间复杂度概念类同，计算方法相似，且在空间充足的情况下其影响可忽略不计，所以主要考虑算法的时间复杂度［12，13］。计算算法时间复杂度的方法主要有两种，一种是计算该算法中所有语句的频度之和，它是该算法所求解问题规模的函数，当用n 表示问题规模时，算法的时间复杂度用T(n)表示。如文献［1］就用该方法对特征提取算法的时间复杂度进行分析，但其结果太过主观，不能准确的对各算法的时间复杂度进行分析比较。另一种是计算算法执行时用到的加减乘除等运算的次数，来分析算法时间复杂度。利用该方法能定量的分析算法复杂度，进而更好的对算法的性能进行分析。为便于比较各种算法，可通过运行时间t(s)衡量算法的时间复杂度［13］，为

式中，ca，cs，cm，cd分别为每种运算一次操作所需时间;函数A，S，M，D 分别为每种运算的次数。由于每种运算在计算机中的运算时间不同，所以可对算法的时间复杂度进行量化表示。

3 特征提取算法时间复杂度分析

根据上文分析，可以计算五种特征提取算法的算法复杂度。

熵特征:由于熵特征提取算法中k 的值一般取2，所以其算法复杂度为

相像系数特征:提取相像系数要分别计算矩形和三角的相像系数，所以其算法复杂度为求去一个相像系数特征的两倍，其算法复杂度为

式中，ce为开方运算的时间。由于除法和开方运算较少，可以忽略，所以其算法复杂度为

模糊函数特征:该特征提取算法分为模糊函数和小波分解算法，所以其算法复杂度为

复杂度特征:该特征由盒维数特征和稀疏性特征构成，所以其算法复杂度为

式中，N0为求取稀疏性特征窗函数的长度;cs为比较运算;clog为对数运算，但对数运算只有一次，可忽略。该算法复杂度可简化为

双谱特征:该特征提取算法分为双谱估计算法和相像系数，所以其算法复杂度为

式(21)可简化为

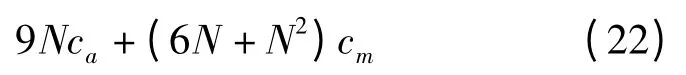
由上述分析可得每种算法的时间复杂度，见表1。

表1 每种算法的复杂度

4 算例分析及仿真实验

Brian.W.K 在文献［14］中对各种运算的运算时间进行了测试，在不同的数据条件下，乘法与加、减、比较运算时间基本相同，而除法运算时间比上述几种运算的运算时间大约多2 ～10 倍。由上文分析的每种算法的时间复杂度公式，结合测试数据可将算法的时间复杂度转化为每种算法的乘法数，见表2。

表2 每种算法的复杂度

由表2 可以得到5 种特征参数时间复杂度由大到下的排序为:BI、AF、CR、C、En。

为验证上文分析的算法复杂度的正确性，下面进行计算机仿真。

首先对5 种特征提取算法的运算时间进行计算，所用计算机平台为Core i3 联想个人电脑，CPU为3.3 GHz，内存为2 GHz，50 次计算的平均结果，见表3。

表3 5 种算法的平均运算时间

由表3 可以得出5 种算法的计算时间与上文分析的算法复杂度是相对应的，而且可以从仿真实验中发现，当算法复杂度中的运算出现平方阶时，其运算时间要远远大于运算为常数阶的算法。这对将来进一步分析算法时间复杂度提供了有力的依据。

为进一步验证上文分析算法复杂度的正确性，选用5 种特征参数对8 类雷达辐射源信号进行分选，假定每种信号分别产生50、100、150、200 个，总数则依次为400、800、1200、1600 个。特征参数依次为AF、CR、C、En、BI 分别称之为参数1 ～参数5;选用的分类器为KFCM 算法，初始聚类数目c =2，最大可能类别个数cmax=8，迭代次数T 设定为50，停止条件ε≤0.001，核函数为高斯径向基核;选择八种雷达辐射源信号，依次为CW、LFM、FSK、BPSK、QPSK、LFM-BPSK、FSK-BPSK 和NLFM 信号，分别称之为信号1 ～信号8。FSK 信号的两个频点分别为24 MHz和36 MHz，FSK-BPSK 信号的两个频点分别为25 MHz 和35 MHz，其余信号的载频均为30 MHz，脉宽均为10 μs，采样频率为120 MHz。LFM 信号的带宽为5 MHz;FSK 信号编码规律为［100110］;BPSK 信号的相位编码规律为［11100010010］;QPSK信号的相位编码规律为［01230312211300112012］;LFM-BPSK 信号的带宽为5 MHz，相位编码规律为［11100010010］;FSK-BPSK 信号的频率与相位编码规律均为［11100010010］;NLFM 信号为正弦调频信号。

所需时间如图1 所示，图中1 ～5 分别表示参数1 ～5。

图1 不同信号个数时的运算时间

由图1 可知，选用不同的特征参数对8 类信号进行分选所需的时间不同，随着信号总数的增加，分选所需时间也逐渐增加。分析其原因，不同特征参数提取的复杂性不同，在提取过程中所耗费的时间也不同。而选用不同特征参数进行分选所用的时间与上文分析的提取算法复杂度相匹配，由此可以证明本文分析的算法复杂度的正确性。

5 结 语

阐述了5 种特征提取算法，之后运用数据结构和算法设计等相关知识对5 种特征提取算法的时间复杂度进行推导，得到其数学表达式，最后通过计算机仿真实验验证了本文推导的特征提取算法时间复杂度的正确性。

［1］HAN JUN，HE MINGHAO，TANG ZHIKAI，et al.Estimating In-pulse Characteristics of Radar Signal Based on Multiindex［J］. Chinese Journal of Electronics，2011，20(1):187-191.

［2］GEXIANG ZHANG，HAINA RONG，LAIZHAO HU，et al.Entropy Feature Extraction Approach of Radar Emitter Signals［C］//Proceedings of International Conference on Intelligent Mechatronics and Automation. 2004:621-625.

［3］ ABDULNASIR YILDIZ，MEHMET AKIN，MUSTAFA POYRAZ，et al. Application of Adaptive neuro-fuzzy Inference System for Vigilance Level Estimation by Using Wavelet-entropy Feature Extraction［J］. Expert Systems with Applications，2009，36(4):7390-7399.

［4］MURAT UYAR，SELCUK YILDIRIM，MUHSIN TUNAY GENCOGLU. An Effective Wavelet-based Feature Extraction Method for Classification of Power Quality Disturbance Signals［J］.Electric Power Systems Research，2008，78(10):1747-1755.

［5］HO K C，PROKOPIW W，CHAN Y T.Modulation Identification of Digital Signals by the Wavelet Transform［J］.IEE Proceedings，Radar，Sonar and Navigation，2000，147(4):169-176.

［6］韩俊，何明浩，朱振波，等. 基于复杂度特征的未知雷达辐射源信号分选［J］. 电子与信息学报. 2009，31(11):2552-2555.

［7］GEXIANG ZHANG，LAIZHAO HU，WEIDONG JIN. Resemblance Coefficient Based Intrapluse Feature Extraction Approach for Radar Emitter Signals［J］. Chinese journal of electronics，2005，14(2):337-341.

［8］ JUN HAN，MING-HAO HE，YAN MAO，et al. A New Method for Recognizing Radar Radiating-source［C］. ICWAPR’2007，4:1665-1668.

［9］LI T J，GUO S B，XIAO X C.Study on Fractal Features of Modulation Signals［J］.Science in China(Series F)，2001，44(2):152-158.

［10］韩俊，何明浩，朱元清，等.基于双谱二维特征相像系数的雷达信号分选［J］.电波科学学报.2009，24(5):848-851.

［11］张贤达.现代信号处理［M］. 第二版.北京:清华大学出版社，2002.

［12］郑宗汉，郑晓明.算法设计与分析［M］. 北京:清华大学出版社，2005:5-29.

［13］SAHNI S.Data Structures，Algorithms，and Applications in C++［M］. Boston:WCB/McGraw-Hill，1998:17.

［14］BRIAN W K，Pike R.程序设计实践［M］.裘宗燕，译.北京:机械工业出版社，2000:341-343.