基于形位公差的公差原则在尺寸链中的应用*

樊富友，于 娟，陈 明，刘 萌，李 斌，陈 卫

(1.中国兵器集团公司长沙机电产品研究开发中心，湖南长沙410100;

2.中航光电科技股份有限公司，河南洛阳471003)

基于形位公差的公差原则在尺寸链中的应用*

樊富友1，于 娟2，陈 明1，刘 萌1，李 斌1，陈 卫1

(1.中国兵器集团公司长沙机电产品研究开发中心，湖南长沙410100;

2.中航光电科技股份有限公司，河南洛阳471003)

阐述尺寸公差与形位公差的关系，分析不同公差原则在设计中的适用范围，介绍形位公差在不同公差原则下的处理方法。通过实例分析计算，应根据装配关系，确定形位公差的增减性，非对称形位公差不能盲目地作为减环引入装配尺寸链中。

形位误差;装配尺寸链;公差原则;极值法;公差分析

1 引言

在设计产品时，除了需要进行强度、刚度及运动等计算外，还需要进行几何精度设计，以保证产品顺利装配和达到所需要的功能要求。另外，产品的质量取决于机械加工精度和装配精度［1］。尺寸链是解决尺寸精度分配和保证装配精度要求的常用方法，但在尺寸链中如何正确处理形位误差成为设计工程师较为难解决的问题［2］。形位误差在产品的制造过程中是不可避免的，传统的公差分析研究是单纯的尺寸精度公差，而很少考虑形位公差［3－4］，得到的公差分析结果有误差，已不能满足产品的要求。形位误差在装配尺寸链中的处理情况在文献［5－8］中得到有益探索。对于武器、航空航天产品既要考虑气动要求，又要满足水平精度测量，形位误差扮演着越来越重要的角色。回避或忽略形位误差的影响，往往造成产品返修或报废。

2 尺寸公差与形位公差的关系

2.1 尺寸公差与形状公差的关系

零件的线段定形尺寸是长度尺寸，平面的定形尺寸有长度和宽度尺寸。由于零件的定形尺寸尺寸公差带与直线度、平面度公差带方向不一致，因此不能用定形尺寸控制直线度、平面度，但高度尺寸采用包容原则，则高度尺寸公差能控制该平面的平面度误差。

圆度公差是限制圆柱体在同一正截面内实际圆对理想圆的变动量。圆柱度是限制实际圆柱体对其理想圆柱体的变动量，所以圆柱体的直径尺寸与圆度、圆柱度有关，尺寸公差能控制相应的圆度、圆柱度误差。

2.2 尺寸公差与定向公差的关系

两点检测实际尺寸，尺寸合格，平行度也可能有较大误差，即独立原则下，尺寸公差不控制平行度误差。包容原则下，尺寸公差控制平行度误差。一般情况下，尺寸公差不能控制垂直度误差;在任何情况下，尺寸公差不能替代控制倾斜度误差。

2.3 尺寸公差与定位公差的关系

轴、孔的定形尺寸与同轴度无关，所以轴、孔的直径尺寸公差不能控制同轴度误差。当同轴度公差采用最大实体原则时，轴孔的定形尺寸公差与同轴度公差有补偿关系。

对称度公差与同轴度公差一样，被测要素的定形尺寸公差不能控制对称度误差，定位尺寸也与对称度公差无关。

位置度公差是被测点、线、面相对其理想要素所允许的最大变动区域。理想要素位置由理论正确尺寸相对于基准而确定的。所以定位尺寸公差与位置度无关。当位置度采用最大实体原则时，被测要素的定形尺寸公差与位置度公差有关，位置度公差能得到定形尺寸公差的补偿。

3 公差原则的适用范围

公差原则分为独立原则和相关要求，相关要求又分为包容要求、最大实体要求，最小实体要求和可逆要求，从孔、轴配合性质，装配互换及其他功能要求出发，合理地选择独立原则或不同的相关要求。

3.1 独立原则的适用范围［9］

(1)尺寸公差与形位公差需要分别满足要求，两者不发生联系的要素，如测量平板的平面度误差。

(2)形位精度要求很高的场合，如滚动轴承内外圈滚道与滚动体的形状误差。

(3)两要素的定形尺寸公差不可能控制他们之间的位置精度的场合，如两对轴承孔的公共轴线中心距与孔的尺寸公差。

(4)零件上未注尺寸公差的要素。

3.2 相关要求的适用范围

(1)包容要求主要用于保证孔、轴配合的配合性质，特别是配合公差要求严格的精密配合，用最大实体边界保证所需的最小间隙或最大过盈。

(2)最大实体要求主要用于只要求装配互换的要素，也用与保证指定的配合性质。

(3)最小实体要求主要用于控制最小壁厚，保证零件强度。控制特定表面到理想导出要素所在位置的最大距离，以保证分度精度或定位精度，获得最佳技术经济效益。

(4)可逆要求只用于被测要素，不用于基准要素。

4 形位公差的处理方法

在尺寸链计算中，一般把封闭环视为组成环的函数进行尺寸公差的计算和分配，传统的尺寸链分析计算很少考虑形位公差对封闭环的影响。实际上，零件要素的尺寸及公差和零件要素的形状、位置公差都影响尺寸链的封闭环。因此，对于不同的零件功能要求应采用不同的公差原则，公差原则不同，在尺寸链分析计算中对形位公差的处理方法也不同。

4.1 独立原则下的形位公差

独立原则是指零件图样上对某要素给出的尺寸公差和形位公差各自独立，彼此无关，分别满足各自要求的公差原则。对于图样上不规定尺寸公差与形位公差相互关系的要素，其形位公差的要求与尺寸的大小无关，就表示它们遵循独立原则。尺寸公差只控制要素实际尺寸的变动量，把实际尺寸控制在给定的极限尺寸范围内，不控制形位公差，而形位公差只控制被测要素的形位公差，与实际尺寸无关。因此，在尺寸链的分析计算中，除了将零件的尺寸公差计入尺寸链外，还应将相应的形位公差作为尺寸链的组成环计入。在绘制尺寸链的过程中，对于形位公差上、下偏差时对称分布的环(如对称度、同轴度等)，无论是是增环还是减环，它们对封闭环的影响是一样的，可按增环简化处理。对于形位公差上、下偏差时非对称分布的环(如平行度、平行度等)，若是轴、孔式(套接)配合的，将形位公差叠加到最大实体上，造成装配间隙减小的，在尺寸链计算中将形位公差作为减环处理;若是对接配合的，将形位公差叠加到最大实体上，造成总尺寸增大的，在尺寸链计算中将形位公差作为增环处理。

4.2 包容要求下的形位公差

包容要求是要求单一尺寸要素的实际轮廓不得超出最大实体边界、且实际尺寸不得超出最小实体尺寸的一种公差原则，其实质就是用零件的尺寸公差控制其形位公差，因此，形位公差对封闭环不产生影响。在尺寸链的分析计算中可以不涉及图样上所注的形位公差，只需计入零件的尺寸及公差即可。

4.3 其它要求下的形位公差

在最大实体要求、最小实体要求及可逆要求的状态下，将零件的形位公差叠加到尺寸公差上，通过实体实效边界条件来满足封闭环的装配要求。

5 应用实例

例1:某弹体由舱段1与舱段2组成，舱段1与舱段2采用对接结构，由轴向螺栓连接，求舱段1与舱段2总长。

采用极值法求解尺寸链。

(1)分析:由以上可知，封闭环为对接舱段总长，舱段1、舱段2为组成环且为增环。

舱段1、舱段2采用独立原则标注，其外形尺寸及实际零件尺寸见图1所示。

图1 舱段外形尺寸及实际零件尺寸图

舱体的A1(300±0.2)、A2(180±0.1)尺寸公差无法控制平行度误差f1(0.1)、f2(0.1)，舱体的实际尺寸应是尺寸公差与平行度误差的综合叠加结果。

(2)计算:尺寸链简图如图2所示。

(3)结果

当舱体两端面同向倾斜变化时，尺寸公差无法控制平行度误差，在本例中，平行度误差作为增环引入尺寸链中。当舱体两端面反向倾斜时，尺寸公差能限制平行度误差，固不在计算平行度误差。

例2:轴与轴套配合尺寸如图3所示，试计算装配间隙。这里假定为小批量生产，零件要求满足完全互换。

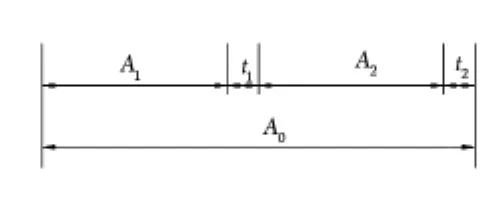
图2 尺寸链简图

图3 轴与轴套的尺寸简图

(1)分析:由以上可知，封闭环为轴与轴套的装配间隙，轴尺寸为减环，轴套尺寸为增环。轴线具有垂直度误差，在装配中对封闭环直接起作用，使作用尺寸增加，因此，垂直度误差作为减环引入尺寸链中。就增环轴套而言，垂直度误差造成配合的作用尺寸减小，可见轴套的垂直度误差作为减环引入尺寸链中。

(2)计算:尺寸链简图如图4所示。

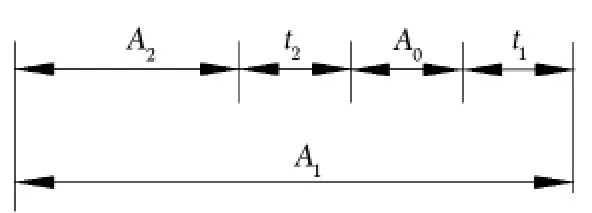
图4 尺寸链简图

通过以上两个简单的例子可知，首先确定封闭环，根据封闭环和装配关系确定形位误差的增减性。

6 结论

(1)形位公差是否计入尺寸链中与公差原则和形位误差的分布状态有关。

(2)在尺寸链计算中，先确定封闭环，根据装配性质确定形位公差的增减性。对于平行度，平面度、垂直度等形位误差不能盲目地都作为减环计入尺寸链中。

(3)不考虑形位公差的尺寸链计算，其结果只能是估算，考虑形位公差后，计算结果接近实际。

［1］ 王基生.具有形位精度的装配尺寸链的简易快速求解［J］.机械，1997，24(4):41－42.

［2］ 同长虹，黄建龙，董世芳.在尺寸链计算中如何考虑形位误差——公差原则在尺寸链计算中的应用［J］.现代制造工程，2008(1):89－91.

［3］ 袁贵星，王 平.蒙特卡洛模拟及其在公差设计中的应用［J］.天津科技大学学报，2008，23(2):61－64.

［4］ 王太勇，熊跃东，路世忠，等.蒙特卡洛仿真法在尺寸及公差设计中的应用［J］.农业机械学报，2005，36(5):102－104.

［5］ 陈 飞，徐学林.尺寸链计算中对称度误差的处理方法［J］.林业机械与土木设备，2006，34(1):37－38.

［6］ 刘燕德，蒋育华，欧阳爱国.考虑形位误差的装配尺寸链计算探讨［J］.江西农业大学学报，2003，23(1):158－160.

［7］ 张 炜.具有形位误差的装配尺寸链的分析计算［J］.甘肃农业大学学报，1997，32(4):327－330.

［8］ 杜官将，薛小强.尺寸链中形位公差的判别与解算［J］.机械工程与自动化，2008(6):164－168.

［9］ 甘永立，吕林森.新编公差原则与几何精度设计［M］.北京:国防工业出版社，2007.

Application of Geometric Tolerance－Based Tolerance Principle in Dimension Chain

FAN Fu－You1，YU Juan2，CHEN Ming1，LIU Meng1，LIBin1，CHEN Wei1
(1.Changsha Electromechanical product Research and Development Center，China South Industries Group Corporation，Changsha Hunan 410100，China;
2.Avic China Aviation Optical-Electrical Technology Co.，Ltd，Luoyang Henan 471003，China)

In this paper，the relationship between dimension tolerance and geometric dimension are described，applicable ranges of different tolerance principles in design are analyzed，and processing methods for geometric tolerance under the different tolerance principles are introduced.By example analysis and calculation，increasing and decreasing of the geometric tolerance is determined according to assembly relationship，and asymmetric geometric tolerance can't blindly serve as a decreasing link to be leaded into assembly dimension chain.

geometric tolerance;assembly dimension chain;tolerance principle;extremum method;tolerance analysis

TG801

A

1007－4414(2013)05－0049－03

2013－08－02

樊富友(1980－)，男，河南驻马店人，硕士，工程师，主要从事工作:结构设计及工艺。