乒乓球轨迹预测的研究与仿真＊

王奇志，杨晓晓

（北京交通大学计算机与信息技术学院，北京 100044）

1 引言

机器人打乒乓球时，需要解决快速运动的乒乓球的跟踪、轨迹预测问题，这些问题是机器人研究领域中的共性和关键问题。轨迹预测是对轨迹跟踪过程在时间轴上的进一步延伸。乒乓球机器人在击球过程中，需要首先判断和预测来球的轨迹，才能给运动控制系统以足够的时间，驱动手臂去击打球。因此，轨迹预测对于机器人击球成功率至关重要。

轨迹预测算法主要分为两类：基于运动学模型的方法和基于经验的方法。

文献[1]采用近似的物理模型对乒乓球运动轨迹进行预测，首先对乒乓球在各个轴向上进行受力分析，列出乒乓球在空中飞行的轨迹方程。当乒乓球与球台发生碰撞时，以乒乓球与球台碰撞前的速度为输入，碰撞后的速度为输出，建立碰撞模型。但是，该方法精确建模比较困难，需要大量的实验以确定模型参数。

1997年，上海交通大学芮庆等人和日本大阪大学宫崎文夫教授合作，首先在理论上研究了关于乒乓球轨迹的预测和仿真算法，提出了一种采用局部加权线性回归算法（Local Weight Regression）的乒乓球轨迹预测算法[2]。该方法的优点是不需要对被控对象建立动力学模型，缺点是需要大量的有效样本，并且无法区分乒乓球是否旋转，难以根据旋转对预测结果进行分析。

在轨迹预测中获得反弹前的乒乓球的速度对于反弹后的轨迹预测至关重要。本文着重对文献[1]的计算反弹前的速度的计算方法进行改进，应用Matlab 6.5对改进算法的可行性进行分析，同时为了直观地分析预测轨迹，设计了基于OPENGL的3D 仿真平台。

2 相关工作

2.1 基于运动学模型的轨迹预测

机器人对乒乓球的轨迹预测，基本分为四个步骤：

（1）轨迹跟踪阶段。将采集到的点进行RANSAC去噪，然后采用基于最小二乘法的多项式拟合方法对运动轨迹进行拟合，结合采集时间计算乒乓球在各个测量点的速度和加速度。

（2）反弹前的轨迹预测。对乒乓球飞行的物理机理进行建模，获得乒乓球飞行的微分方程，求解乒乓球的轨迹和速度。

（3）乒乓球与球台的碰撞。主要是构造乒乓球与球台的碰撞模型。

（4）反弹后的轨迹预测。与反弹前轨迹预测采用相同的方法。

2.2 乒乓球飞行模型

乒乓球在空气中运动的过程中，主要受到两个力的作用：重力G＝mg 和空气阻力F＝kv2，其中m 为乒乓球的质量，g 为重力加速度，k 为空气阻力系数。飞行模型参见文献[1]。

（1）水平方向上：

水平方向的Y 轴，具有和X 轴一致的位置预测表达式。

（2）垂直方向上：

2.3 乒乓球与球台碰撞模型

要对乒乓球的轨迹做出准确的预测，除了建立飞行过程精确运动方程之外，还需要对乒乓球与桌面的碰撞进行建模，得到比较准确的反弹模型。碰撞模型的建立参见文献[1]。

反弹模型在X、Y 方向的速度变化用一阶多项式来表示：

其中，kx、ky、bx、by是反弹参数。

垂直方向的反弹模型为：

其中，kz是反弹参数。

反弹模型对反弹前的初始点的速度敏感，没有采用公式推导计算反弹前的速度，而是提出了将预测的轨迹用最小二乘法拟合求导得到反弹前的速度。从实验结果可以看到预测效果很好。

3 算法改进

3.1 初速度反馈调节

在轨迹预测过程中，建立的方程表达式与初始点有关，所以初始点的选取对轨迹预测的精确度影响很大。另一方面，由采集到的10个点进行曲线拟合求导，则计算的速度在一定程度上也会产生误差，所以文献[1]采用了基于位置负反馈的方法对求导得到的速度值进行校正。利用预测与采样点之间的偏差构成反馈回路，调整过程为：

文献[1]中K＝0.005，为定值。本文中：

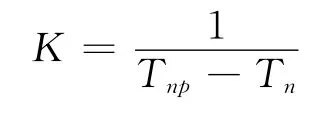
其中，K 是一个动态的系数。这样：

表示预测的坐标误差与时间的比值，表示一个平均的速度误差，它是一个动态修正的系数。

经过多次实验证明，提高了预测结果的精确度。如图1所示，图a1、图b1、图c1为固定比例系数时三个轴上的轨迹预测示意图，右列为动态系数调节时三个轴上的轨迹预测示意图。其中，星号表示跟踪得到的乒乓球轨迹，圆圈表示预测的轨迹。

Figure 1 Chart of track prediction comparison（feedback regulation coefficient）图1 轨迹预测对比图（反馈调节系数）

表1为固定比例系数时预测的坐标及误差，表2为动态系数反馈调节时预测的坐标及误差。由表1和表2可以看到，改进后的系数预测更加准确。

Table 1 Predicted coordinate and error of the fixed proportion coefficient表1 固定比例系数时预测的坐标及误差

Table 2 Predicted coordinate and error of the dynamic coefficient feedback regulation表2 动态系数反馈调节时预测的坐标及误差

3.2 反弹前初速度的计算

反弹模型对反弹前的初始点的速度敏感，文献[1]采用公式推导计算反弹前的速度，本文提出将已经预测好的轨迹用最小二乘法拟合求导得到反弹前的速度。从实验结果可以看到预测效果很好。图2是轨迹预测对比图，左列是用文献[1]提出的方法进行的预测，右列是用本文提出的方法来预测乒乓球反弹后的轨迹。

为了更直观地看到预测效果，公式推导和曲线拟合求解反弹前速度和误差如表3 和表4 所示。坐标中的点是反弹后预测的连续四个坐标值及其误差值。

Table 3 Predicted coordinate and error of the formula calculating before a rally表3 公式推导计算反弹前速度时预测的坐标及误差

4 实验结果与分析

4.1 Matlab 6.5 实验结果分析

实验结果如图2所示，其中三幅图的横坐标均为时间（s），星号表示实际的观察位置，圆圈表示预测的位置。由于乒乓球拍的左右宽150mm，上下高156 mm，因此，对轨迹预测的误差有一定的容忍度，实际误差50mm 以内可以满足击球作业的要求。从表2和表4可看出，X 轴、Y 轴、Z 轴三个坐标轴的误差总和均小于50 mm，所以预测效果符合控制要求。

Table 4 Predicted coordinate and error of the curve fitting before a rally表4 曲线拟合求解反弹前速度时预测的坐标及误差

4.2 OpenGL仿真结果

通过OpenGL仿真平台真实地再现预测轨迹和采样轨迹。如图3所示，图中点状线为采样的轨迹，实线为预测的轨迹。根据这种具有真实感的对比，可以看到预测结果比较好。

Figure 2 Chart of track prediction comparison（calculating rebound before initial velocity）图2 轨迹预测对比图（计算反弹前初速度）

Figure 3 Chart of predicted trajectory and sampling trajectory图3 真实再现预测轨迹和采样轨迹

5 结束语

机器人打乒乓球的一个关键是对乒乓球的飞行轨迹进行准确的预测，进而提前计算得到击打点的位置和速度信息。本文主要是对乒乓球飞行轨迹预测中采用的运动学模型[1]的算法进行改进。实验结果表明，比例系数的改进以及反弹前初速度计算的改进都能够更加准确地预测乒乓球的轨迹，满足打乒乓球作业的要求。

[1]Zhang Zheng-tao，Xu De，Yu Jun-zhi.Research and latest development of ping-pong robot player[C]∥Proc of the 7th World Congress on Intelligent Control and Automation，2008：4881-4886.

[2]Rui Qing，Hu Zong-wu.Research of using LWR learning table tennis orbit prediction simulation[J].Robot，1998，2.（5）：373-377.（in Chinese）

[3]Zhang Yuan-hui.Based on real-time visual table tennis robot calibration and tracking technology[D].Hangzhou：Zhejiang University，2009.（in Chinese）.

[4]Anderson R L.Understanding and applying a robot ping-pong player's expert controller[C]∥Proc of IEEE International Conference on Robotics and Automation，1989：1284-1289.

[5]Hashimoto H，Ozaki F，Asano K，et al.Development of a ping-pong robot system using 7degrees of freedom direct drive arm[C]∥Proc of SPIE 0856，IECON'87，1987.dio：10.1117／1912.943015.

[6]Shreiner D，Woo M，Neider J，et al.OpenGL programming guide：The official guide to learning OpenGL[M].Fourth ed.Deng Zhen-xiang，translation.Beijing：The people post and Telecommunications Press，2005.（in Chinese）

[7]Woo M，Neider A，Davis T，et al.OpenGL programming guide[M].Seventh ed.translated by Wu bin，Duan hai-bo，Xue feng-wu.Beijing：China Electric Power Press，2001.（in Chinese）

附中文参考文献：

[2]芮庆，胡宗武.用LWR 学习进行乒乓球轨道预测的仿真研究[J].机器人，1998，2.（5）：373-377.

[3]张远辉.基于实时视觉的乒乓球机器人标定和轨迹跟踪技术[D].杭州：浙江大学，2009.

[6]Shreiner D，Woo M，Neider J，et al.OpenGL编程指南[M].第四版.邓郑祥，译.北京：人民邮电出版社，2005.

[7]Woo M，Neider A，Davis T，et al.OpenGL 编程权威指南[M].吴斌，段海波，薛凤武，译.北京：中国电力出版社，2001.