铝型材在线切割的PMSM控制系统仿真研究
张刚,廖冬初
(湖北工业大学电气与电子工程学院,武汉 430068)
0 引言
铝型材首先通过挤压机挤出,再经过多道工序,最后传送到切割台进行切割。过去对铝型材的切割方式是以人工控制切割为主,切割精度不能保证,生产效率也不高,这种切割方式逐渐被淘汰。现在一般采用在线切割为主,手工切割为辅的切割方式。在线切割主要要求切割小车的移动速度与型材挤出速度保持同步,否则就会影响切割质量[3],这样控制小车运动的动力系统就显得格外重要。永磁同步电机(PMSM)采用永磁体为转子,没有励磁损耗,且PMSM具有体积小、重量轻、过载能力大、效率高、结构简单、维护方便、运行可靠、易于控制等优势[1,5],所以选用PMSM为切割小车的动力源。本文在分析铝型材在线切割的工作流程的基础上,建立以PMSM为控制系统的仿真模型,并给出仿真模型结构图和仿真结果波形。
1 切割系统的工作流程
为了能够准确分析高速且精确的切割过程,把切割小车在轨道上的反复运动过程分为准备、加速、跟踪、反向加速、反向匀速返回和归位六个状态,切割小车的速度控制曲线如图1所示。
首先切割系统进入准备工作状态,在这个状态中,切割机处于等待传送轨道上的铝型材,此时系统通过编码器对挤出的铝型材进行测量,并将信号反馈给控制器,控制器根据一定的控制算法处理后,若发现测量的长度与设定的切割长度相差为设定值时,切割小车开始以最大的加速前进,这个过程称为加速状态。加速状态要求用时最少,使切割小车以最短的时间达到铝型材运行的速度,从而进入跟踪并切割状态。在跟踪并切割状态下,控制器不断处理编码器的反馈信号来计算铝型材的速度和长度,从而调整切割小车的速度。当切割小车和铝型材相对静止且铝型材的切割长度在允许误差范围内时,启动切割机,注意在切割时要始终保持切割小车的速度与铝型材的运行速度同步,5s后发出停止切割信号,使切割机停止切割,切割完成后,切割小车进入反向加速返回状态。在这个状态中切割小车首先做减速运动使其速度为0,然后使控制小车的永磁同步电机反转,并以最大反向加速度加速到设定的最大返程速度,进入到反向匀速返回状态。当切割小车以匀速返回到接近的设定初始位置时,再次使切割小车做减速运动而进入归位状态,当切割小车的速度减速到0时,切割小车停止并正好回到设定的初始位置,从而完成整个切割周期。然后切割系统再次进入准备切割的工作状态,重复以上的六个状态完成全部铝型材的在线切割。

图1 切割小车速度控制曲线图
2 PMSM磁场定向的控制策略分析
永磁同步电机的数学模型是一个非线性、多变量和强耦合的复杂系统[1]。为了使永磁同步电机的控制方式像直流电机的控制方式一样,在此,我们选用了磁场定向的矢量控制方法。这样就可以实现对定子电流的控制来控制PMSM的转矩。
磁场定向控制就是对交流电机的控制参数进行解耦,从而实现对交流电机的线性化控制。在PMSM中,将0dq旋转坐标系放在转子上,随着转子一起同步旋转。在实际检测电路中,是不能检测到0dq坐标系上的变量的,而是检测三相电流ia、ib、ic,这样就必须通过坐标变换把定子电流的合矢量在0dq旋转坐标系上进行解耦,即。通过位置传感器对转子位置的检测可以 知 道与 d 轴 的 夹 角θ, 则,对于凸装式转子电机,,根据电磁转矩方程:

式中:Pn为转子的极对数,fψ为转子磁链,由于转子是永磁结构,其fψ为常数。

图2 PMSM矢量控制原理图
由图2可以看出,整个原理框图是由位置环、速度环及电流环组成的三闭环反馈系统,系统主要包括三相电流检测模块、位置速度检测模块、坐标变换模块、PI调节器模块及逆变器控制模块。由图可以知道对切割小车的控制流程为,首先给定位置信号与检测到的切割小车的位置信号相比较后,通过PI控制器得到速度给定信号*ω,然后速度给定信号与检测的速度信号做差后,其差值通过PI控制器得到电流给定信号,最后由磁场定向控制方式给定=0以及由速度变换得到的信号,同时与通过检测到的三相电流经坐标变换而反馈的id,iq作比较,它们的差值通过PI控制器而得到在0dq坐标系上的轴电压Ud、Uq,再由坐标变换为0aβ坐标系上的轴电压Vα、Vβ,利用SVPWM控制算法得到驱动逆变器的六路PWM驱动信号,最终达到跟踪控制的目的。
3 PMSM控制系统模型的建立
在MATLAB环境下建立如图3所示的PMSM磁场定向控制系统的仿真模型。

图3 PMSM磁场定向控制系统的仿真模型
此仿真模型中主要包含了坐标变换模块、PI控制模块、SVPWM模块、功率变换模块和电机及测量模块。
3.1 坐标变换的仿真实现
在PMSM数学模型中有相对于定子的ABC静态坐标系、0aβ静态坐标系和相对于转子的动态0dq坐标系。在控制系统中主要通过控制0dq坐标系上的轴电流轴电压来实现电磁转矩控制,所以必须将ABC静态坐标系的变量转化为0aβ静态坐标系的变量,再由0aβ静态坐标系的变量转化为转子动态0dq坐标系的变量。
因为三相电流对称性即:

所以三相电流转化为0αβ轴上的电流如式(3):

Park变换是指0aβ坐标系向转子0dq坐标系的转化,通过Park可以变换出id,iq、其变换方程如式(4):

由式(2)(3)(4)可以得到ABC坐标系到0dq坐标系的转化方程如式(5):

由方程(5)可以得到由ABC坐标系到0dq坐标系变换的仿真模型如图(4)所示。

图4 ABC到0dq坐标变换模型
图中u1为ia,u2为ib,u3为sinθ,u4为cosθ,Fcn1为u(1)*(u(4)+(sqrt(3)/3)*u(3))+u(2)*(2*sqrt(3)/3)*u(3),Fcn2为u(1)* ((sqrt(3)/3)*u(4)-u(3))+u(2)*(2*sqrt(3)/3)*u(4)。
Park逆变换是指0dq坐标系向0αβ坐标系的转换,通过Park逆变换可以将Ud、Uq转换为Vα、Vβ。其逆变换方程式如下:
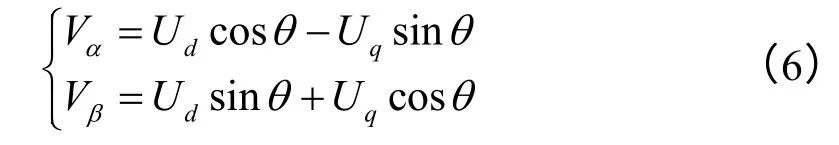
根据方程式(6)可以得到Park逆变换的仿真模型如图(5)所示。

图5 Park逆变换模型
图中u1为Ud,u2为Uq,u3为sinθ,u4为cosθ,Fcn3为 u(1)*u(3)+u(2)*u(4),Fcn4为u(1)*u(4)-u(2)*u(3) 。
3.2 SVPWM算法的仿真实现
逆变器的脉宽调制采用SVPWM控制技术,SVPWM具有数学模型简单、控制线性度好和容易实现等优点。其原理如图6所示。它以三相正弦波电压供电时交流电机的理想磁通轨迹为基准,用逆变器的8种开关模式产生的实际磁通去逼近基准磁通圆,使电机获得幅值恒定的圆形磁场(即正弦磁通)[4],从而达到较高的控制性能。
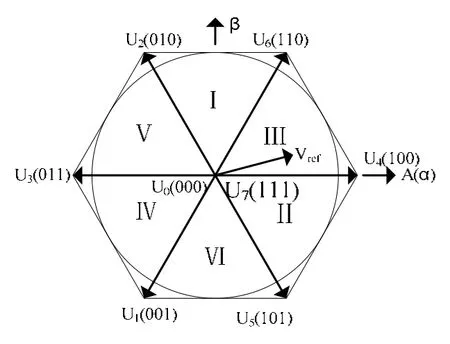
图6 SVPWM原理图
如图6,以第Ⅲ扇区为例说明合成矢量与基本矢量之间的对应关系,根据矢量的合成原理可知:
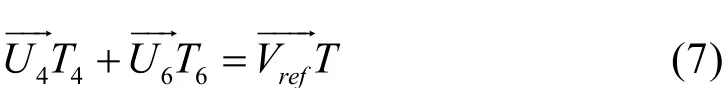
式中U4、U6为两个相邻基本矢量,T4、T6为分矢量上的作用时间,Vref为合成矢量,T为PWM周期。由(7)式及图6,将合成矢量分解到0aβ坐标系如下式:

根据SVPWM原理,图6中的六个基本矢量的幅值均为2Udc3,其中Udc为逆变侧的直流电压,为了计算的方便,系统中所有变量均采用的是标幺值。所以基本矢量取相对于最大相电压,基本矢量的幅值变为,代入上式可以得:

同理可以计算出其它扇区基本矢量的作用时间,在此定义:

则对应于上面计算的第Ⅲ扇区U4、U6上的作 用 时 间T4=-Z、T6=X,同 理 在 其 他 扇区 中的基本矢量作用时间也可以用X、Y、Z三个变量来表示,他们之间的对应关系可以用如表所1示:

表1 不同扇区基本矢量作用时间
PWM波形的软件实现方法很多,目前比较流行的是7段式电压空间矢量PWM波形。根据空间矢量所在的扇区不同,三组IGBT的切换时间如表2所示:

表2 不同扇区IGBT的切换时间
其中定义:

从上面两个表可知,空间矢量所在扇区判断的正确与否是保证IGBT切换的关键,在此,定义三个变量A、B、C,利用前面的X、Y、Z三个变量的值来计算,若X>0,则A=1,否则A=0;若Z<0,则B=1,否则B=0;若Y<0,则C=1,否则C=0;所以扇区号N=A+2B+4C。
由上述SVPWM控制原理,SVPWM模块的仿真模型如图7所示。

图7 SVPWM仿真模块
3.3 仿真结果
仿真中采用的永磁同步电机是以台达伺服电机(ECMAC30604)为仿真对象。电机额定功率P=400W,额定转速 n=3000r/min,额定转矩T=1.27N·m,转动惯量J=0.28×10-4kg·m2,定子电阻R=1.55Ω,电机电感L=0.00671H,极对数Pn=5。在仿真中对位置环作如下处理,位置环的给定信号采用与时间有关的一次函数,反馈信号为电机旋转的机械角度。模拟切割小车往返的负载转矩均为1 N·m。得到定子三相电流、转子转速、位置跟踪的波形如图8、9、10所示。

图8 三相定子电流
由图8可以看出在电机从静止到转动或从转动到停止电流脉动都较小,突然改变负载系统能够很快进入稳定状态。由图9可见,电机的正向加速和反向加速都能够瞬时达到稳定速度状态,在速度跟踪和返回阶段电机转速都很稳定,从图中可以看出转子速度完全符合切割小车的工作流程。由图10可见,位置能够完全跟踪。
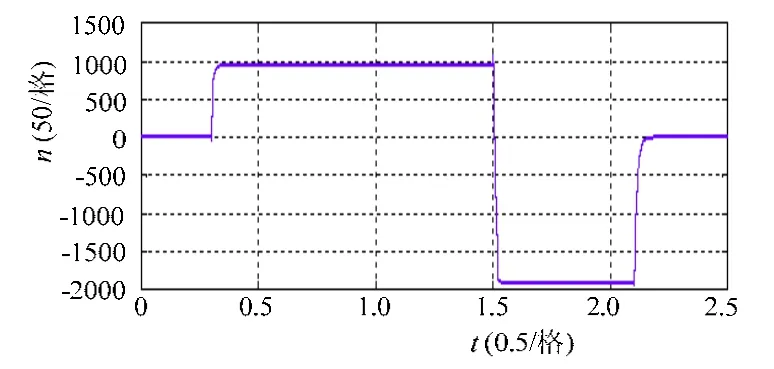
图9 转子转速

图10 位置跟踪
4 结论
本文在分析铝型材在线切割中切割小车工作要求的基础上,选用永磁同步电机作为其动力系统,并灵活运用磁场定向的矢量控制策略,搭建了基于MATLAB的PMSM控制系统的仿真模型,根据实际电机的参数给定,最终达到了预期的结果。在对电机的等系统的仿真模型中,使用MATLAB软件是一种很有效的研究方法,既可以省略很多繁琐的计算,也可以有效的将理论与实际相结合,而且最终结果可靠。
[1] 张成, 王富东, 罗力恒, 等. 采用双自由度PI速度控制器的PMSM矢量控制仿真研究[J]. 工业控制计算机, 2011, 24(3): 58-60.
[2] 王晶菡, 李铁才, 杜坤梅. 基于Matlab的永磁同步电机控制系统仿真研究[J]. 宁波职业技术学院学报,2007, 11(2): 1-4.
[3] 张铮, 郑文超, 陈水胜, 等. 铝型材生产线同步定长切割系统[J]. 湖北工业大学学报, 2009, 24(4):28-30.
[4] 王晓明. 电动机的DSC控制—微芯公司dsPIC应用[M]. 北京:北京航空航天大学出版社, 2009:176-185.
[5] 缪孟良. 永磁同步电机DTC与SVPWM控制方法比较研究[D]. 福建: 厦门大学, 2007:35-43.

