曲线匹配法在雷达动态标校中的应用

练学辉，李 伟，蔡文彬

(1.海军驻南京地区雷达系统军事代表室，南京 210003;2.中国船舶重工集团公司第七二四研究所，南京 210003)

0 引言

在雷达动态标校过程中，需要通过硬件或软件的方法对雷达测量的目标距离、方位、仰角的系统误差进行修正，以提高测量精度。目前，常用的方法是通过校准雷达和真值设备的系统时间，然后根据数据时戳匹配雷达测量数据和真值数据，并对真值数据进行坐标转换，再通过匹配后数据得到测量值与真值的误差并计算出系统误差，根据系统误差进行误差修正［1-2］。这种方法简单方便，易于实现，但前提是必须保证系统的数据时戳精度在可容忍范围内。对于处于相邻位置的两个系统来说，只需要建立数据通信，进行时间对时就可以完成时间同步，使两个系统的时间误差在可容忍的范围内;但对于架设在不同区域的设备来说，上述方法不易实现。同时，即使实现了系统之间的时间对时，但每个设备内部的时间延时也需要考虑，如不能正确估量则延时的程度不同所引起的误差也不尽相同。为了避免不可估量的时戳精度对系统差的影响，本文提出一种曲线匹配的方法。这种方法不以时间作为匹配条件，而是将目标运动参数曲线进行匹配，通过使目标运动轨迹重合，得到系统误差，进行误差修正［3］。

图1 修正前和修正后的雷达目标与真值目标轨迹图

1 时间匹配法

目前，雷达标校一般采用时间匹配法，是通过比较两个系统跟踪目标的数据时戳，使用数据率较高的真值数据的时间匹配数据率较低的雷达测量数据，查找时间差最小的两组数据，然后再根据雷达时戳将真值数据插值到相同时间进行真值比较。

采用时间匹配法标校的过程一般有以下几个步骤:

(1）系统对时 由雷达向真值设备发送时统报文，真值设备根据时统报文进行时间校准;

(2）目标跟踪雷达发现目标并稳定跟踪后，向真值设备发送目标参数，引导真值设备跟踪同批目标;

(3）数据记录雷达和真值设备各自发送跟踪的目标信息至数据采集设备，目标信息一般包括系统时间、目标标识、距离、方位、仰角等信息;

(4）坐标转换 由于雷达与真值设备的架设位置不同，所跟踪的目标数据之间存在位置偏差，需要根据架设位置的差值将真值设备跟踪的数据进行坐标转换;

(5）数据分析 对采集的雷达数据和真值数据进行匹配，计算雷达与真值设备跟踪参数的误差。

在分析数据时，首先将超差的个别异常数据剔除。需要剔除的异常数据包括:

(1）初始建航但航迹尚未稳定的数据;

(2）航迹即将丢失时的数据;

(3）误差大于3 倍精度的数据。

然后，通过计算真值方位和雷达方位、真值仰角和雷达仰角的差值，得到方位差和仰角差数据。然后，对方位差和仰角差数据进行分析处理，根据有效数据的方位差和仰角差计算出方位和仰角的系统误差。接着，根据系统差对雷达的方位和仰角进行修正，修正后再进行标校。此时，标校结果的系统误差应趋向于0，否则系统误差修正不成功，需重新标校修正。

2 曲线匹配法

曲线匹配法是在直角坐标系中用散点图绘制目标运动轨迹，分别以方位、仰角为横轴和纵轴，在同一幅图中分别绘制雷达目标运动轨迹和真值目标运动轨迹［4］。可以使用Excel 或Matlab 绘制，然后比较两条曲线是否重合;如果不重合，说明两个系统之间存在系统差，需要通过修正系统差将两条运动轨迹匹配，如图1所示。

从图1(a）可看出，两条曲线没有完全重合，接下来就是通过对雷达系统的系统误差进行修正，使雷达目标运动轨迹图与真值目标运动轨迹图重合，如图1(b）所示。

本文设计了曲线匹配算法来计算系统误差并完成曲线匹配，具体算法如下:

(1）遍历雷达测量数据，针对雷达测量数据Zi在真值数据中寻找与其距离差值最小的n 条真值数据;

(2）将n 条数据各自与Zi的距离差值与门限值λ 进行比较，将大于门限λ的数据去除;

(3）计算Zi与门限判断后剩余数据的X 误差和Y 误差均值，求得相对于雷达测量数据Zi的AveXi和AveYi;

(4）遍历所有雷达数据，对每条数据都进行上述处理，然后计算所有AveXi和AveYi的均值，求得AveX和AveY，即系统误差。

3 两种方法的对比与分析

使用曲线匹配法的优点就是无须两个系统的精确对时，只要记录两个系统跟踪的目标数据，然后将它们的跟踪数据对应为相同目标，来实现系统误差标校工作。在试验中，通过移动雷达目标运动曲线，使两条轨迹重合，此时方位上、仰角上移动的数值即为方位系统差和仰角系统差。

以相同航路上两批目标为例，图2 是使用时间匹配法计算出误差后绘制的误差折线图，图3为使用曲线匹配法绘制的目标运动轨迹图。

从图2中可以观察到，由于雷达系统与真值系统的时间之间存在误差，因此使用时间匹配法计算出的方位、仰角误差较大，并且左右两图中方位和仰角的系统差不一致。

从图3中可以观察到，使用曲线匹配法将两条曲线匹配之后并没有出现图2中所示的误差特别大的点。因此，使用曲线匹配法时无须考虑两个系统的量测数据时戳是否完全同步。

图2 时间匹配法计算的误差

图3 曲线匹配法计算的误差图

同时，对比图2和图3，分别对比左右两图，可以看到图2左右两图计算的系统差差别较大，而图3中显示两目标得出的系统差非常接近。系统差数值见表1。此外，使用曲线匹配法时还可以观察到目标航迹的跟踪是否稳定，如图4和图5所示。

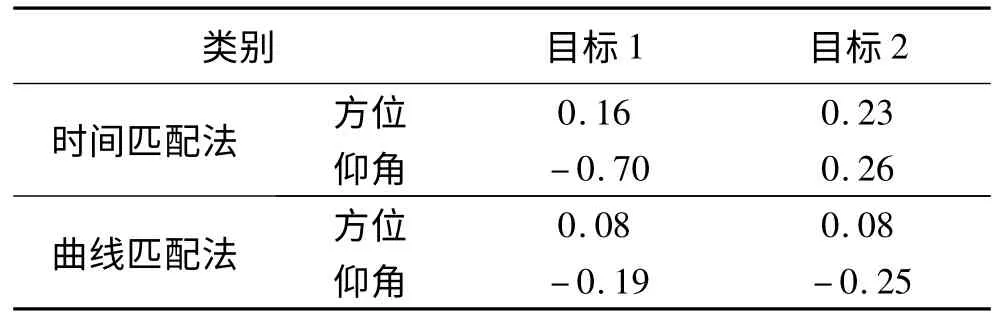
表1 相同航路两批目标的系统差

图4(a）为修正前轨迹图，图4(b）为修正后轨迹图。从图中可以发现，两条曲线不能完全重合，原因是跟踪数据异常，因此此组数据不能用来统计系统差。而如果采用时间匹配，发现此段数据并没有超差，仅从做差数据上发现不了跟偏的问题。如果将此段跟偏数据代入计算系统差，将会影响系统差的准确性。同样，图5中在方位239°及245°时跟踪偏离的问题也可以在比较的同时发现，也不会影响对使用曲线匹配法计算的系统差。

但是，曲线匹配法并不能通过任何目标运动轨迹计算出系统差。当目标的运动轨迹是直线或近似直线时，由于使两条轨迹重合的系统差不唯一，此时无法确定系统差的值。图6为一次试验中雷达目标与真值目标的运动轨迹图。因为两条曲线几乎呈平行直线的关系，所以无法通过曲线匹配法进行修正。因此，使用曲线匹配法需要目标的运动轨迹不能为直线，最好选择过顶飞行目标或方位有转向的航路上的目标。

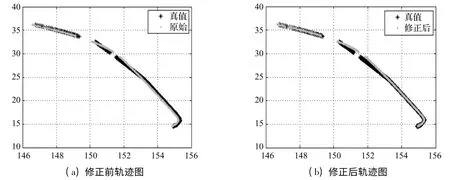
图4 目标运动轨迹(一）

图5 目标运动轨迹(二）

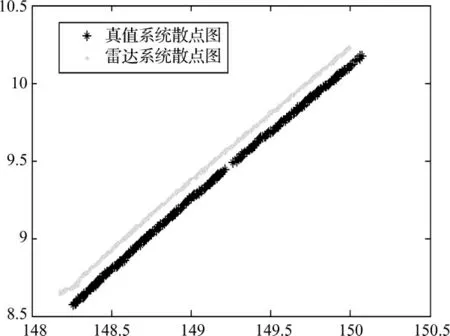
图6 目标运动轨迹(三）

4 结束语

通过对比分析发现，在两个系统的数据时戳精确匹配的情况下，时间匹配法简单有效，只需要将两个系统的数据一一对应，直接做差，即可得出系统差。而如果两个系统中数据时戳精度较差时，时间匹配法将不使用。此时，曲线匹配法能够很好地计算出系统差，可将目标运动轨迹进行匹配，而无须剔点，从而能够发现雷达跟踪过程是否稳定。它能够应用于所有场合，但目标参数曲线必须要有拐点。

曲线匹配法是通过移动曲线进行曲线重合匹配以达到误差修正的目的，通过数据修正处理，使得雷达目标轨迹图和真值目标轨迹图重合。本方法已在某雷达与ADS 真值系统的动态标校试验中得到应用，效果良好，后续将进行曲线自动匹配算法的进一步探索与研究。

［1］罗军，商允力，等.应用AIS信息进行岸基对海雷达标校［J］.电讯技术，2009(9）.

［2］朱起悦.应用差分GPS技术进行雷达标校［J］.电讯技术，2006(1）.

［3］田伟.雷达精度试验中GPS 数据坐标转换及误差分析［J］.雷达与对抗，2007(2）.

［4］苑文亮，唐小明，等.基于ADS-B 数据的雷达标校新方法［J］.舰船电子工程，2010(3）.