基于小波神经网络的GPS高程异常拟合模型探究

刘 浩,徐 南

(河海大学 地球科学与工程学院,江苏 南京 210098)

GPS因具有全球性、全天候、连续性、高精度等导航定位的特点近年来在测量中得到了广泛的应用,在精确测定目标的平面坐标的同时还可以测定其高程坐标,有效地减小了测量的劳动强度并提高了工作效率,因此如何有效地利用GPS进行高程测量以减少普通几何水准量测是目前一个重要的课题。然而GPS采用WGS-84坐标系,测定的高程值是测站点沿法线方向到参考椭球面的距离(大地高H),而我国采用是正常高高程系统,需测定测站点沿重力线方向到似大地水准面的距离(正常高Hγ),两者之间存在的差值——高程异常ξ=H-Hγ,因此精确测定高程异常值 ξ对于用GPS高程测量代替普通几何水准测量具有重要意义。目前高程异常值拟合的主要模型有:平面拟合模型、二次曲面拟合模型、多项式拟合模型、移动曲面拟合模型、薄板小挠度变形模型拟合模型、多面函数拟合模型等[1]。这些模型为用GPS高程测量部分代替几何水准测量提供了可能,但仍存在精度较低等缺陷。近年来学者们针对神经网络做了大量研究,神经网络已经成为人工智能、认知科学、信号处理、模式识别、知识处理等相关领域的热点。神经网络因具有很强的鲁棒性、容错性和学习能力,能够很好地逼近复杂函数,这为利用神经网络高精度地计算高程异常提供了可能。

1 神经网络模型

1.1 BP神经网络

BP神经网络是最典型、目前应用最广泛的一种人工神经网络。该网络是一种前向网络,分为输入层、隐藏层、输出层;主要特点是信号前向传递,误差反向传递。理论研究表明,只要有足够多的隐含层神经元,三层人工神经网络可以无限地逼近任何线性和非线性函数。但BP神经网络也有一些固有缺陷,如算法容易陷入局部极小点、预测精度低、收敛速度慢等,这些缺陷限制了它在工程中的进一步应用[2]。

1.2 小波神经网络

小波神经网络是近年来新兴的一种人工神经网络,充分继承并融合了小波变换和神经网络两者的优点。其思想是用已定位的小波函数代替Sigmoid函数作为激活函数,通过仿射变换建立起小波变换与网络系数之间的连接并应用于函数逼近。与前向的神经网络相比,小波神经网络依据小波分析理论确定其基元和整个结构,可避免BP神经网络等结构设计上的盲目性,此外小波神经网络不仅充分利用了小波变换的时频局部化特性而且具有更灵活有效的函数逼近能力和较强的容错能力,可有效克服普通人工神经网络模型固有的一些缺陷[3-4]。

小波神经网络以BP神经网络拓扑结构为基础,将小波基函数作为隐含层节点的激活函数,信号向前传播的同时误差反向传播的神经网络。

小波神经网络训练步骤如下[5]:

(Ⅰ)网络初始化:随机初始化小波函数的平移参数和伸缩参数以及网络连接权重并设置网络学习速率;

(Ⅱ)样本分类:将样本分为训练样本和测试样本,其中训练样本用于训练网络,测试样本用于测试网络预测精度;

(Ⅲ)预测输出:将训练样本输入网络,计算网络预测输出、网络输出和期望输出的误差;

(Ⅳ)权值修正:根据(Ⅲ)的误差修正网络权值和小波函数参数,使网络预测值逼近期望值;

(Ⅴ)判断算法是否结束,若没有结束则返回(Ⅲ)。

小波变换实质就是通过一个基本小波函数φ(x)平移或伸缩构成一族小波函数系去表达或逼近一个函数。论文使用的小波基函数是Morlet小波,其表达式为:

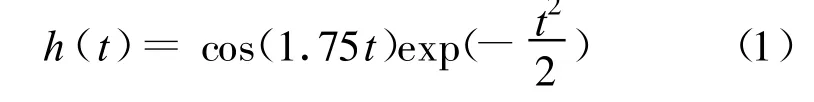
2 试验分析

文献[6]共有34个GPS点的高程异常数据,本文除了要比较BP神经网络和小波神经网络两种神经网络模型的效果,还要和文献[6]模型进行比较,因此作者选择了10个与文献[6]相同的点作为两种神经网络的训练样本,利用BP神经网络模型和小波神经网络模型分别计算另外24个GPS点的高程异常数据,如表1所示。

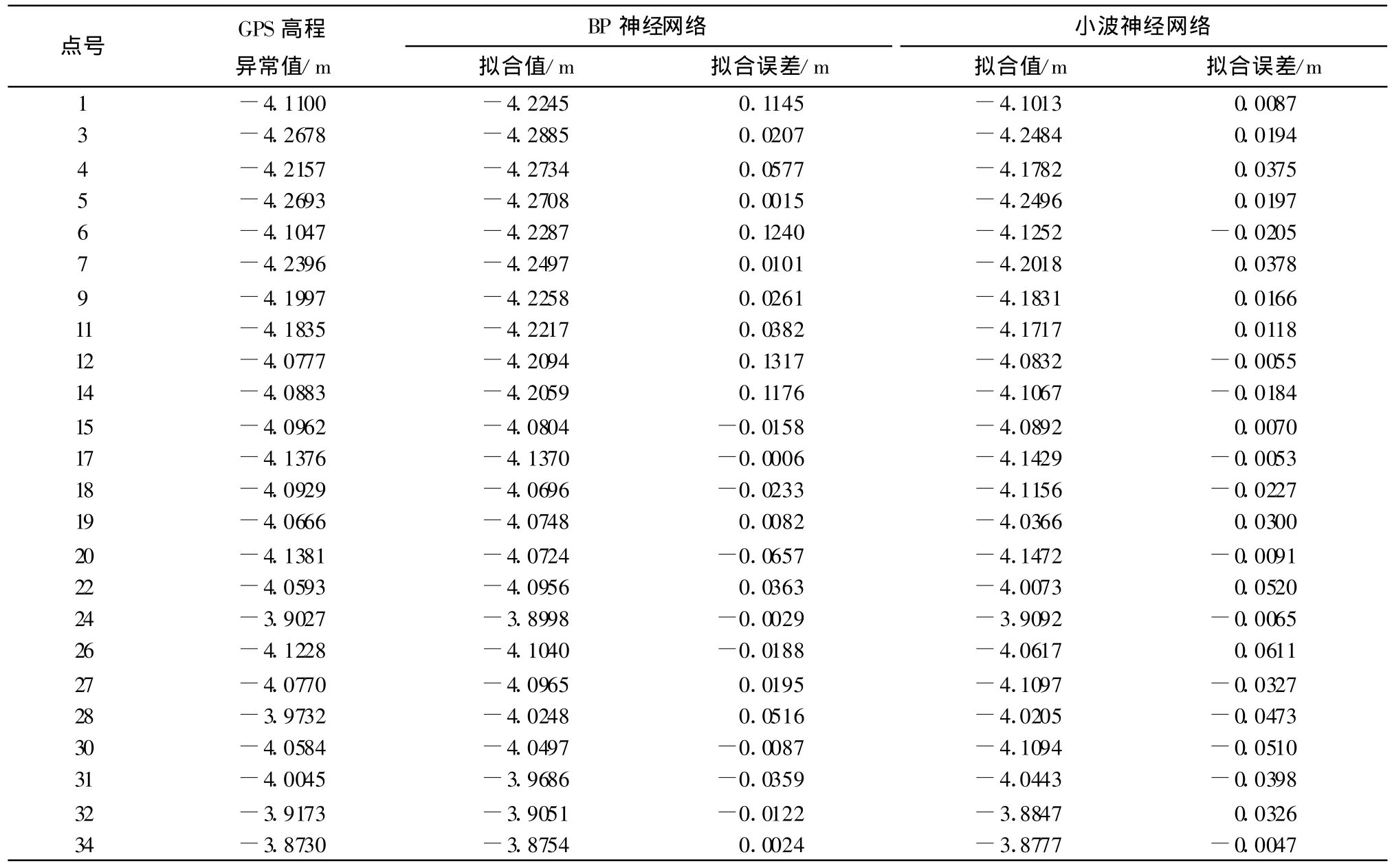
表1 利用两种不同神经网络模型进行GPS高程异常数据拟合的结果

表2 不同模型进行GPS高程异常拟合的精度

根据表1、表2的数据,可以看出在文献[6]提供的数据下,小波神经网络模型拟合中误差0.0306 m最小,文献[6]模型拟合中误差0.0411 m次之,BP神经网络模型拟合中误差0.0579m最大,说明小波神经网络模型拟合的结果较其它两种模型而言精度更高。

将三种不同模型对GPS高程异常拟合的结果和GPS高程异常值绘制在一起,如图1所示;将三种不同模型对GPS高程异常拟合的误差值绘制在一起,如图2所示。从图1和图2可以看出,小波神经网络模型对高程异常的拟合结果和GPS高程异常值比较接近,表现出了较高的精度,文献[6]的模型次之,BP神经网络模型的拟合结果和GPS高程异常值相比出现了较大的浮动,说明小波神经网络模型拟合的结果精度相对更高些。

图1 GPS高程异常拟合结果

图2 GPS高程异常拟合误差

3 总 结

高精度地确定高程异常是利用GPS进行高程测量一项非常重要的工作,因此高程异常拟合模型的选择显得尤为重要。本文选择了BP神经网络和小波神经网络两种神经网络模型,介绍了其基本原理,利用两种神经网络模型分别计算了高程异常的拟合结果和拟合误差。从表1、表2可以看出,文献[6]模型中误差为0.0411 m,BP神经网络模型中误差为 0.0579 m,而小波神经网络模型中误差为0.0306 m;图1、图2更形象地说明小波神经网络模型拟合结果和GPS高程异常值最为接近,证实了小波神经网络模型具有较高的拟合精度。

综上,可以得出在实验数据下小波神经网络模型比其它两种模型更优,证明了小波神经网络在GPS高程异常拟合方面具有较强的实用性。

[1]岳仁宾.GPS高程拟合模型及其应用研究[D].重庆:重庆大学,2008.

[2]桂现才.BP神经网络在MATLAB上的实现与应用[J].湛江师范学院学报,2004,25(3):79-83.

[3]郑小洋,叶仲泉.Legendre小波神经网络[J].重庆大学学报(自然科学版),2003,26(8):48-51.

[4]李 逊,谢红胜.基于遗传算法的小波神经网络[J].计算机与数字工程,2007,35(8):5-7.

[5]史 峰,王小川.Matlab神经网络30个案例分析[M].北京:北京航空航天大学出版社,2011:208-210.

[6]付云文,袁 伟.组合模型在GPS高程转换中的应用[J].西华大学学报(自然科学版),2011,30(6):30-33.