基于物元可拓法对郑州市地表水水质评价

陈南祥,汤 泽

(华北水利水电学院资源与环境学院,河南 郑州 450011)

随着人口的逐步增加,郑州市人均当地水资源占有量为198.8 m3,不足全国平均水平的1/10。同时,城市化、工业化的迅速发展和对水资源的认识不足,造成河湖水质恶化、生态系统遭到破坏、城市污水排放严重等一系列问题。因此,对地表水水质评价是环境质量评价的一项重要内容,也是进行有效的环境管理的重要手段之一。目前,地表水水质评价方法有多种,主要有模糊综合评价法[1]、人工神经网络法[2]、层次分析法,因子分析法、GIS模型评价法和灰色系统法等[3-6]。本文主要采用由蔡文教授创立的物元可拓法[7],它能有效地解决多指标和由单项指标评价结果不相容的问题,建立评价事物多指标质量评定模型,直接求出关联度,对水质进行等级评价,避免了在评价中水质指标值界于两个相邻级别时,很难准确判断其属于哪个级别的问题[8]。但物元可拓法对水质评价也存在一定的局限性,若待评物元的特征值超出了节域范围,在计算综合关联度时就会出现相等的状况。在这种情况下,就无法计算综合关联度,所以需要从多方面去分析水质情况。

1 物元模型的构建

物元可拓理论是研究物元关系和可拓性及物元变换规律,描述事物变化和与矛盾转化的形式化语言。在可拓数学中,采用关联函数的概念把逻辑值域从[0,1]扩展到(-∞,+∞)实数轴,把所解决的矛盾问题定性化和定量化。

1.1 物元分析

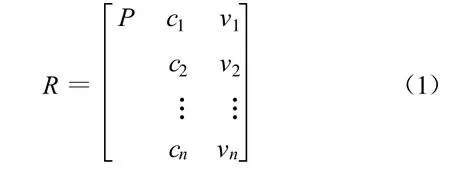
给定事物的名称P,它关于特征C的量值V,以有序三元组R=(P,C,V)作为描述事物的基本元素,简称物元[9]。若事物P有多个特征量c1,c2,c3,…,cn表示,其相应量值用v1,v2,v3,…,vn来描述,则称n维物元,用矩阵表示为:

1.2 经典域、节域和待评物元的确定

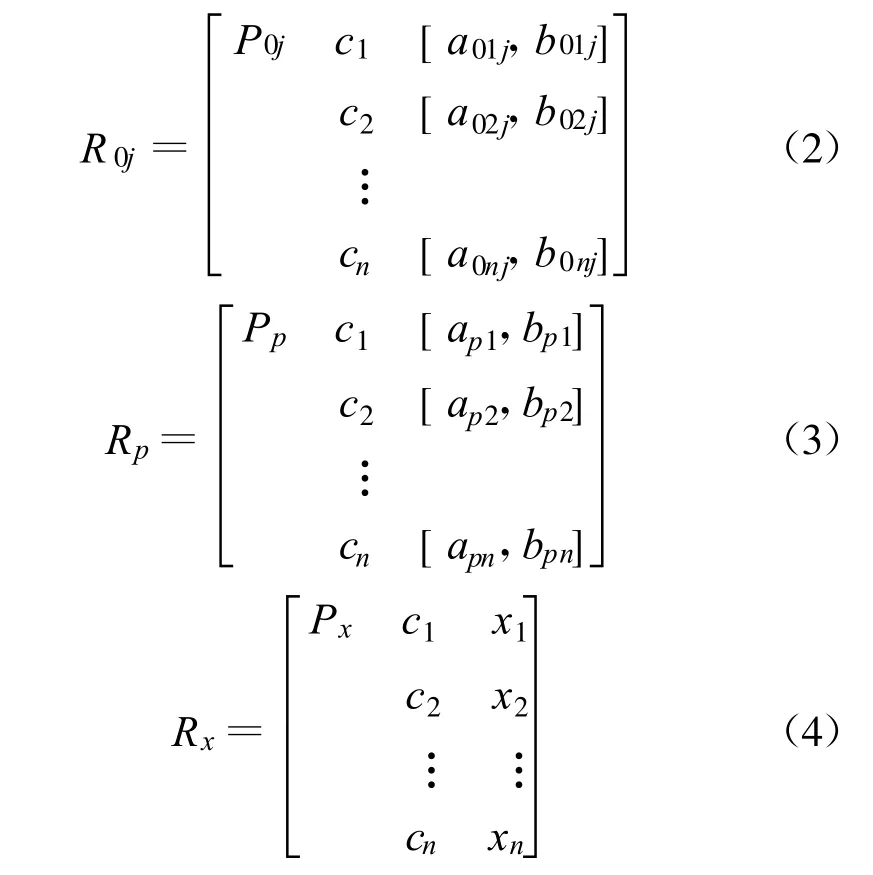
当事物P0j为第j等级标准时,其特征cij取值范围为[a0ij,b0ij],经典域为式(2);由标准值和实测值来确定节域Rp,其特征ci取值范围为[api,bpi],为式(3);由实测值确定待评物元Rx,其式为(4)。

1.3 关联函数与关联度的确定

关联函数:

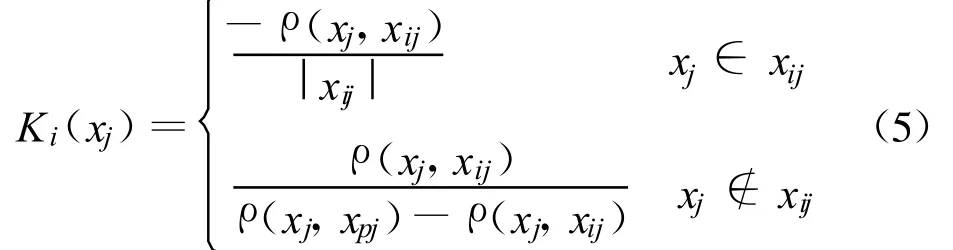
式中 ρ(xj,xij)为点 xj与区间xij的距离;ρ(xj,xpj)为点xj与区间xpj的距离。若区间x0取值范围为[a,b],则点xj到区间x0=[a,b]的距离公式:

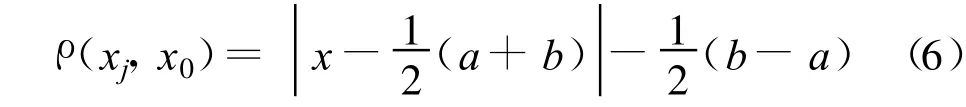
且Ki(xj)表示各评价因子关于评价级别的关联度。

1.4 综合关联度和评价等级

待评事物Px在第j级的综合关联度为:

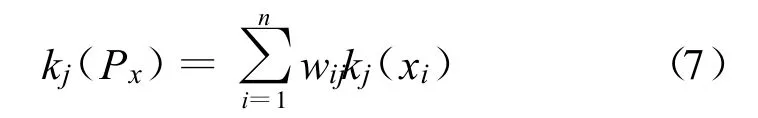
式中:kj(xi)的数值表示评价单元符合某标准范围的隶属程度;wij为各评价因子的权重。根据最大隶属度原 则,kj(Px)=max{k1(Px),k2(Px),…kn(Px)}。kj(Px)≥1,被评价对象超出标准对象上限,其值越大,说明开发潜力越大;0≤kj(Px)≤1,被评价对象符合标准对象隶属程度的要求,其值越大,越接近标准要求上限;-1≤kj(Px)≤0,被评价对象不符合标准对象要求,但具有转化为标准对象的条件,其值越大,越容易转化;kj(Px)≤-1,被评价对象既不符合标准对象要求,也不具备转化为标准对象的条件。

2 物元可拓法在郑州地表水水质评价中的应用

本文以郑州市河流评价为例,选取6个监测点,采用《地下水质量标准》(GB/T14848—1993)[10]作为评价的标准,将水质级别划分为五级,并以PH(c1)、DO(c2)、COD(c3)、高锰酸盐指数(c4)、BOD5(c5)、NH3-N(c6)、总磷(c7)、总氮(c8)八项指标作为评价因子,各指标采用2012年实测值,见表1。

2.1 数据归一化处理

每个评价因子的量化值区间范围不完全相同,有的评价因子以数值越小级别越高;有的则以数值越大级别越高,为了便于结果的比较,需对各评价指标和评价标准进行数据归一化处理[11]。

对于数值越小级别越高的评价指标归一化公式:

对于数值越大级别越高的评价指标归一化公式:

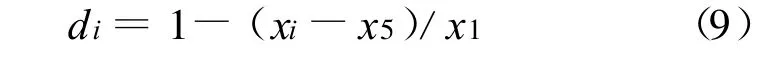
式中 :di、xi、x1、x5分别为归一化后的标准值 、未归一化的标准值、Ⅰ级和 Ⅴ级标准值。归一化后的评价标准见表2,归一化后的实测值见表3。

2.2 确定权重

评价因子权重的确定方法有很多,本次研究根据层次分析法[12],运用AHP软件,计算出各监测点 的各监测指标的权重,计算结果见表4。

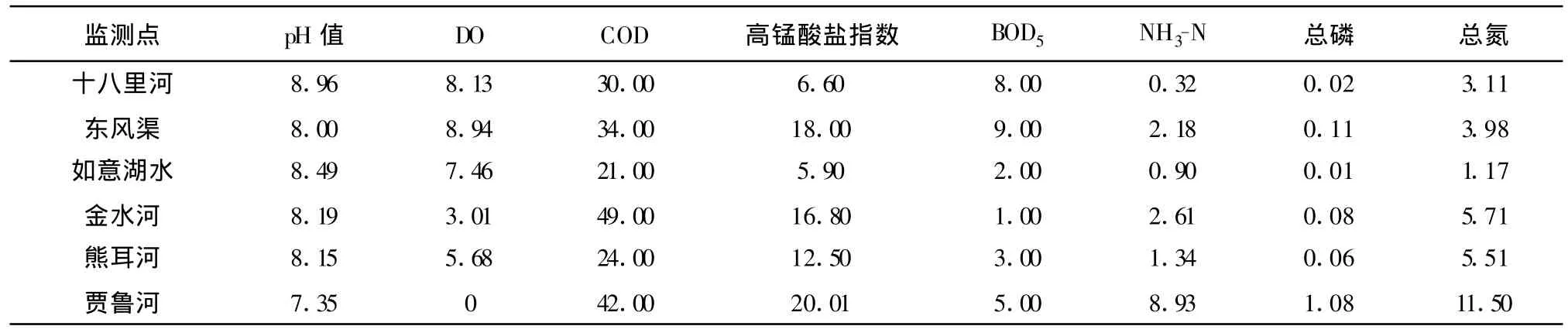
表1 各评价因子在6个监测点的监测值 单位:mg/L

表2 归一化后的分级标准值 单位:mg/L

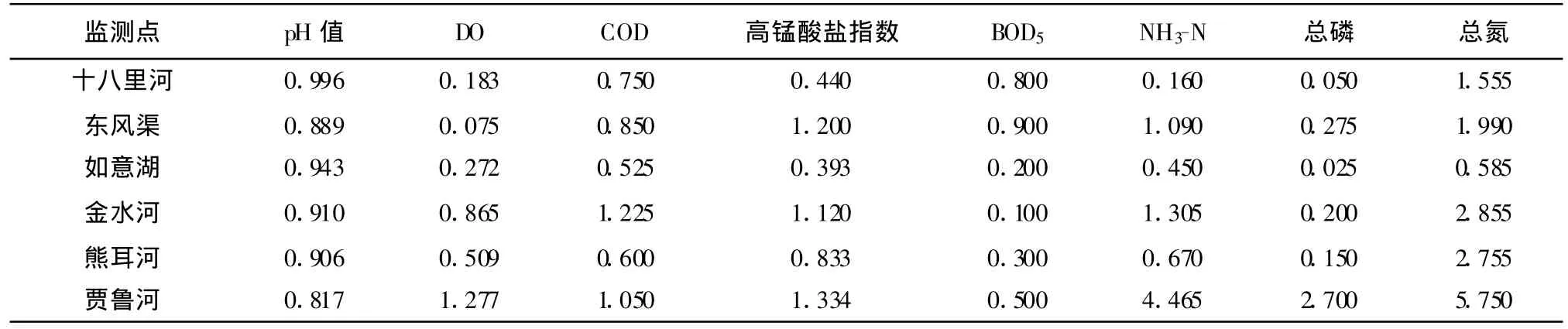
表3 归一化后的监测值 单位:mg/L

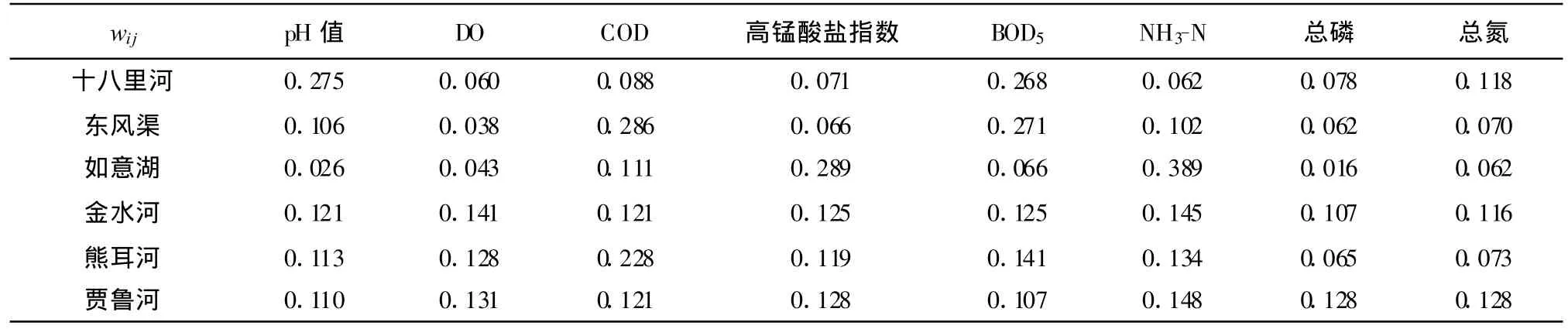
表4 各监测点的各监测指标的权重

2.3 确定监测点综合关联度及评价等级

根据经典域,节域和待评物元的定义,以及表2、表3,由式(2)～式(6)可得十八里河各评价因子关于评价级别的关联度,计算结果见表5。

通过表4和表5,运用综合关联度公式(7),k1(p)=-0.557,k2(p)=-0.508,k3(p)=-0.6,k4(p)=-0.426,k5(p)=0.018。根据最大隶属度原则,综合关联度为 k5(p)=0.018,所以十八里河水质为Ⅴ类水,水质污染严重。

按照上述步骤,利用物元可拓法分别计算6个监测点的综合关联度,计算结果见表6。

根据等级评价原则,选取最大隶属度,由表6可见,十八里河水质等级为Ⅴ类水,且不接近标准最大上限值;东风渠水质等级为Ⅴ类水;如意湖水质等级为Ⅲ类;熊耳河水质等级为Ⅳ类水;由于金水河和贾鲁河综合关联度都小于0,但数值都在区间[-1,0]之间,所以评价对象不符合标准对象要求,但具有转化为标准对象的条件,且金水河数值大于贾鲁河,说明金水河更易转化,同时它们都属于类Ⅴ类水。根据评价结果可以得到,水质由好到坏的顺序:如意湖、熊耳河、十八里河、东风渠、金水河、贾鲁河。

表5 十八里河各水质指标与各水质类别的关联度

表6 各监测点关于各水质类别的关联度

2.4 计算结果对比

为验证本文方法的合理性和可行性,采用模糊综合评价法对各监测点进行水质评价,并与本文方法进行对比,见表7。

表7 结果对比

从对比结果可以得出,两种方法评价结果基本相同。所以,基于物元可拓法的地表水质评价结果可信,评价结构也验证了该评价模型的可靠性。

3 结 语

(1)选取了郑州市6条河水质样本,采用8个评价因子,利用基于物元可拓法的水质评价模型进行水质综合评价,其评价结果与模糊综合法评价结果基本一致,说明物元评价模型可靠,可用于水质的综合评价。

(2)根据综合关联度可知郑州市地表水水质总体较差,为了促进生态系统的可持续发展,需要加大力度进行治理,以达到郑州市生态需水的标准。

[1]邓超冰.海水水质的模糊综合评价模型的比较[J].海洋环境科学,1993,12(2):22-28.

[2]孙 涛,潘世兵,李永军.人工神经网络模型在地下水水质评价分类中的应用[J].水文地质工程地质,2004,31(3):58-61.

[3]李如忠.水质评价理论模式研究进展及趋势分析[J].合肥工业大学学报(自然科学版),2005,28(4):369-373.

[4]罗定贵,王学军,郭 青.基于MATLAB实现的ANN方法在地下水质评价中的应用[J].北京大学学报(自然科学版),2004,40(2):296-302.

[5]周林飞,许士国,孙万光.基于灰色聚类法的扎龙湿地水环境质量综合评价[J].大连理工大学学报,2007,47(2):240-245.

[6]刘章军,叶燎原.模糊概率模型及其在地下水水质评价中的应用[J].应用基础与工程科学学报,2007,15(3):286-293.

[7]蔡 文.物元模型及其应用[M].北京:科学技术文献出版社,1994.

[8]张先起,梁 川.基于熵权的模糊物元模型在水质综合评价中的应用[J].水利学报,2005,36(9):1057-1061.

[9]门宝辉,粱 川.水质量评价的物元分析法[J].哈尔滨工业大学学报,2003,35(3):358-361.

[10]中华人民共和国地质矿产部.GB/T14848—1993.地下水质量标准[S].北京:中国标准出版社,1993.

[11]刘雷雷,盖 美.水质评价物元分析模型及其应用——以大连英那河水库为例川[J].水资源研究,201l,32(1):6-8.