Seepage model and experiments of drag reduction by nanoparticle adsorption*

GONG Wei (龚玮), DI Qin-feng (狄勤丰), WANG Xin-liang (王新亮), HUA Shuai (华帅),

ZHANG Ren-liang (张任良), YE Feng (叶峰)

Shanghai Institute of Applied Mathematics and Mechanics and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China, Email: gwsuri@sina.com

Seepage model and experiments of drag reduction by nanoparticle adsorption*

GONG Wei (龚玮), DI Qin-feng (狄勤丰), WANG Xin-liang (王新亮), HUA Shuai (华帅),

ZHANG Ren-liang (张任良), YE Feng (叶峰)

Shanghai Institute of Applied Mathematics and Mechanics and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China, Email: gwsuri@sina.com

(Received November 19, 2012, Revised April 3, 2013)

The hydrophobic nanoparticle (HNP) adsorption is a new technique of drag reduction, which changes the wettability of the porous walls of the core, generates the slip-boundary of the fluid flow and consequently enhances the oil recovery. In the present work, a seepage model with consideration of the slip effect in the micro-channels and the influence of the equivalent pore radius modified by the HNP adsorption is proposed based on the Darcy’s law. The permeability of the non-wetting phase in the porous media is calculated according to its dependence on the slip length, while the slip length is determined by a function of the contact angle and the equivalent pore radius. Numerical simulations are performed by use of the COMSOL multiphysics, and an acceptable agreement between experimental and simulation results is achieved (with an error less than 2.5%). The present model can then be used for the mechanism investigation and the prediction of the oilfield performance.

seepage model, slip effect, drag reduction, nanoparticle adsorption, permeability

Introduction

The fluid flow in an oil reservoir is a complex seepage behavior and can be described by a seepage model approximatively. The seepage model for onephase flows was first established by Darcy, and the first seepage model for two-phase flows in porous media was developed by Douglas and Peaceman[1]in 1959. Since then, different seepage models were proposed for different seepage’s flows for various oil recovery enhancement methods in petroleum engineering[1-4]. In 1968 Zeito[2]put forward seepage models for the polymer flooding according to the viscoelastic characteristics of polymer, and Roshanfekr et al.[3]followed the similar studies in 1991. In 2001, Zhao[4]put forward a seepage model for the microbial enhanced oil recovery with consideration of the microorganism’s growth, the metabolism and the migration. These seepage models are all based on Darcy’s law and are the modification of the basic models in essence.

The drag reduction based on the hydrophobic nanoparticle (HNP) adsorptions is a new technology to enhance the oil recovery, which changes the wettability of the core porous walls and generates the slipboundary for the fluid flow[5,6]. The lab and field experiments show that this new technology greatly reduces the water injection pressure and can enhance the water injection rate effectively[7,8]. The essential mechanism of this technology is the slip effect due to the adsorptions of HNPs. Some seepage models describing the flow behavior with consideration of the slip effect in the micro channels were proposed[9-12], which are used mainly for the slippage effect in the gas flow. In the oil industry, because the slip effect is more remarkable in the gas flow than in the liquid flow, therefore, the slip effect in the wetting fluid is often ignored. In this paper, considering the slip effect, a seepage model is proposed for the drag reduction by theHNP adsorption method, and then the core displacement experiments are carried out for its validation. Finally, simulations are carried out to reveal the discrepancy of the pressure distribution due to the HNP adsorptions with the COMSOL Multiphysics.

1. The mechanism of drag reduction by nanoparticle adsorption

In the development of the petroleum industry in China, the proportion of low permeability oil fields is in increase continuously, and therefore, it is of great significance to exploit low permeability oil fields. The water injection is the main method to enhance the oil recovery in low permeability oil fields, but the problems of high injection pressure and low injection volume rate have to be faced. Two methods are used to solve these problems. One is through reservoir stimulations to take measures, such as the acidification and the hydraulic fracturing, which reduce the drag by increasing the pore size, but the reservoir may be contaminated if the method fails. The other is the surface modification method, such as the drag reduction technology by using surfactant and by using HNPs.

The drag reduction technology by the HNP adsorption is a new physical method to reduce the flow resistance in reservoir micro-channels. The HNPs enter into the reservoir micro-channels to form a strong or super-hydrophobic adsorption layer on the micro-channel walls. In the process of water injection, the slip effect of fluid flows is caused by the super-hydrophobic properties of the adsorption layer due to the micro or nanoscale rough structure of the adsorption layer. Simultaneously, the nanoparticle adsorption layer can effectively prevent the contact between the injection water and the clay on the micro-channels walls, to avoid the expansion of the clay.

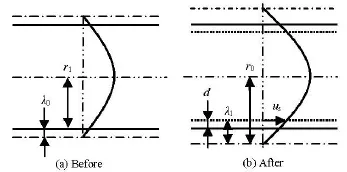
Fig.1 Sketch of slip effect before and after adsorption

The slip effect is the essential mechanism of the drag reduction technology by the HNP adsorption. It is related with the slip velocity on the super-hydrophobic adsorption layer and is always expressed by the slip length. When the slip length of micro-channels is larger than the thickness of the HNP adsorption layer, the effective aperture is larger than the actual pore diameter, and the slip effect plays a part in reducing the flow resistance, and then the nanoparticle adsorption method could reduce the injection pressure. This principle can be described as in Fig.1, wheresuis the slip velocity,0ris the initial aperture,dis the diameter of HNPs,0λis the initial slip length, and1λis the slip length after the HNP adsorption.

2. Seepage models

Since the Darcy’s law was proposed in 1856, it has become the basic equation for studying hydraulics behavior. Combined with the mass conservation equation and the energy conservation equation in the process of flow, the basic seepage models for an oil reservoir are as follows:

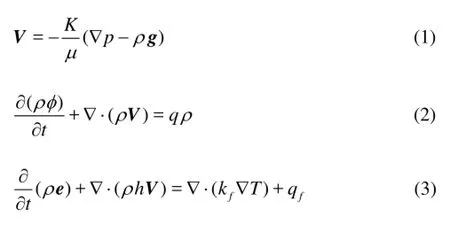
whereVis the apparent velocity,Kis the permeability,μis the dynamic viscosity,gis the gravity acceleration,ρis the density of the fluid,pis the pressure,φis the porosity,Tis the temperature,his the specific enthalphy,eis the specific energy,qis the strength of the source or the sink, andfqis the heat energy.

In an oil field development technology, all the seepage models of a common water flooding method are based on the above modified basic seepage models. For example, in the oil displacement process with surfactant, the surfactant can reduce the capillary forces and free the trapped oil, and the mass fraction of the surfactant changes during the flooding. Therefore the seepage models of the surfactant flooding are established by modifying the mass conservation Eq.(2) in the basic seepage models[13]. In the oil displacement process with polymer, the polymer can increase the apparent viscosity and decrease the permeability of the aqueous phase. Different polymer in this technology usually has different physical properties (e.g., viscoelasticity), as a result, not only the mass conservation equation but also the viscosity itemμof the seepage models need to be modified[14]. In the oil displacement process with microbial flooding, the microbe has special features such as growth, metabolism, reproduction.

The appropriate mass conservation equation becomes very important. Considering that the microbial sediment will lead to the change of the permeabilityKand the porosityφ, and the microbial migration will lead to the change of the velocityV, so the basic seepage Eqs.(1)-(3) should also be modified to fit the flooding[15]. Similarly, in order to establish the appropriate seepage models for the drag reduction technology by the HNP adsorption, the slip effect and the influence of the reservoir porosity and the permeability by the HNP adsorption should be taken into account.

3. Assumptions

(1) The fluid flow in the porous media follows the Darcy’s law, i.e.,Re＜5.

(2) The reservoir is isothermal.

(3) The phase of the fluid is water.

(4) The porous medium is isotropic, the rock and the fluids are slightly compressible.

(5) Gravity is ignored.

(6) Nanoparticles are monolayer adsorptive.

Fig.2 Single pipe model

4. Modeling

The micro-channel of the oil reservoir enjoys various characteristics, such as the multiscale nature, the variable sections, and the strong twists. So it is difficult to describe the structure of the micro-channels accurately. Consequently, a single circular tube model (as shown in Fig.2) is usually used to simplify the model of the core, where 0R,Lare the radius and the length of the core sample, respectively,0ris the radius of the circular pipe. According to the studies of Carman[16],0rcan be calculated by the following formula.

wherekis the permeability measured with gas, 0φis the initial porosity,τis the tortuosity.

In fact, in 1823, Navier proposed a slip boundary condition that the fluid velocity on a surface is proportional to the shear rate at the same point, but the value of the slip length is difficult to determine. Zhang et al.[17]proposed a slip length formula by using the lattice Boltzmann method,

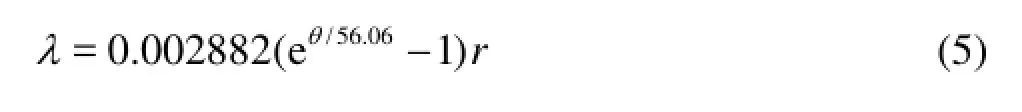
whereθis the contact angle,λis the slip length.

Therefore, the radius1rafter adsorption is

Furthermore, considering the effect of the pressure and the variation of the porosity caused by the HNP adsorption, the final porosity can be obtained by

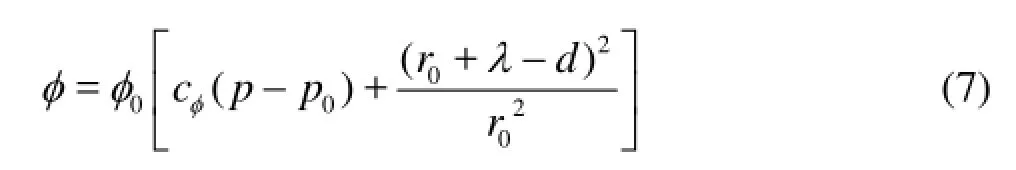
wherecφis the porosity compressibility,0pis the reference pressure,0φis the porosity under0p. There are two parts in Eq.(7), the first one is contributed by the pressure, and the second one is caused by the HNP adsorption.

For the single circular pipe model, a formula for the flow rate can be obtained as in the Hagen-Poiseuille flow,

According to the Darcy’s law, another formula of the flow rate can be obtained as

Comparing Eqs.(8) and (9), the formula of the permeability is obtained as

After the HNP adsorption, there is not only a slip effect, but also a reduction of the aperture, so the permeability after adsorption is

Comparing Eqs.(10) and (11), the permeability with the HNP adsorption is

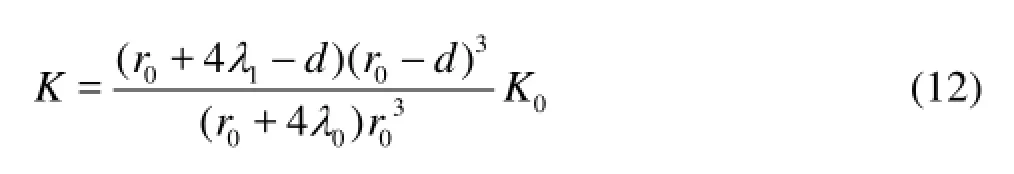
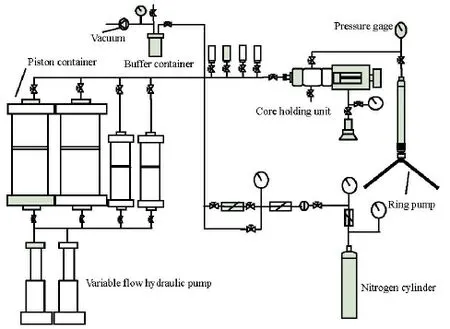
Fig.3 Core flow installation

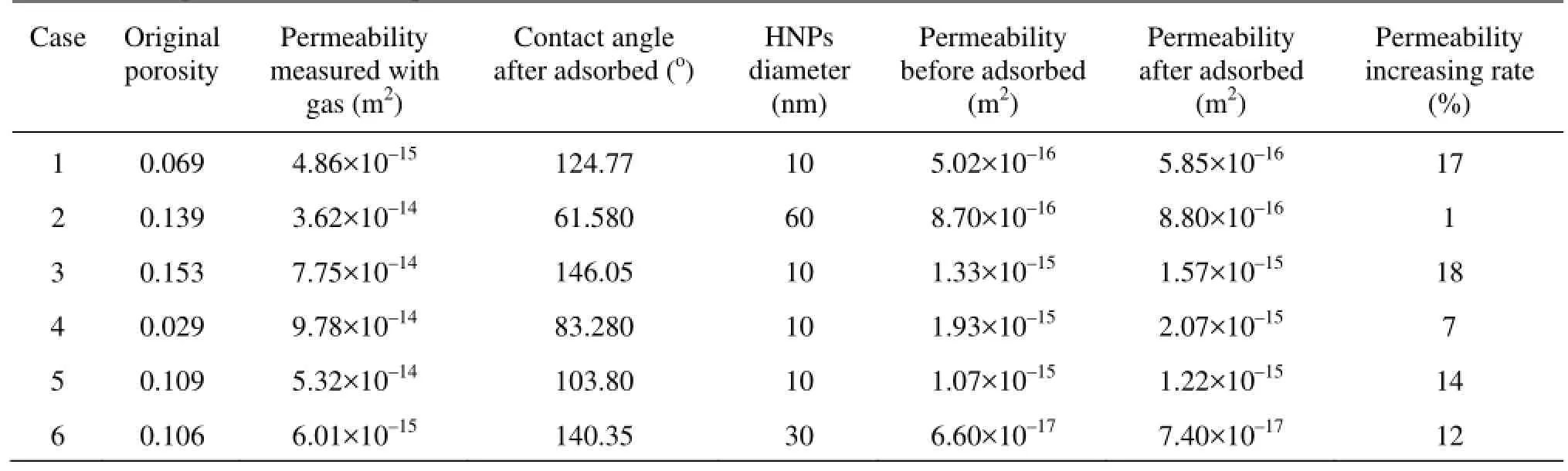
Table 1 Core parameters and experimental results

Substituting Eq.(12) into Eq.(1), we obtain the velocity

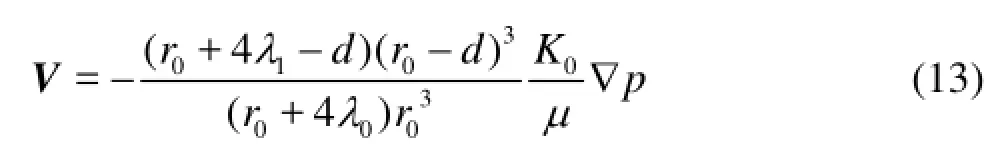
Considering the micro compressibility of the fluid, the density can be obtained as

wherefcis the fluid compressibility, and0ρis the density under0p.

Substituting Eq.(13) into Eq.(2), the seepage model of the drag reduction technology by the HNP adsorption is obtained as

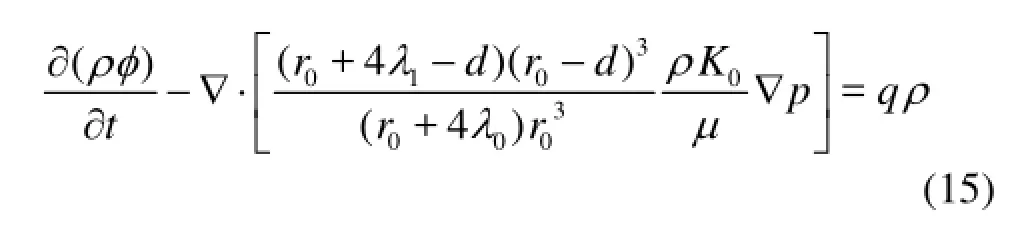
where the porosityφand the densityρare calculated by Eqs.(7) and (14).

5. Model validation and simulation

In this paper, the core flow installation (Fig.3) is applied to evaluate the water injection rate enhancement. Six core experiments with different initial permeabilities were carried out to study the influence of the HNP adsorption on the flow characteristics. The physical parameters and the experimental results of the core samples No.1-No.6 are listed in Table 1. Here, the zero degree of the contact angle is determined by experiments of all six cores before being adsorbed. It is shown that after the HNP adsorption, the permeability of the cores is improved significantly, and the largest increase rate is about 18%.

According to the seepage model proposed in this paper, the permeability for the above 6 cores is calculated to compare with the experiment results (seeTable 2). In order to further illustrate the validity of the model, the calculated results based on the previous model without considering the slip effect are given at the same time. The results in Table 2 show that the previous results contain a large error and show a completely different changing tendency. It is because the previous model does not consider the slip effect, which is the main mechanism of the drag reduction technology by the HNP adsorptions. On the other hand, as the slip effect is taken into account on the flow performance, a very accurate prediction is made by the new seepage model, and the prediction errors are all less than 2.5%, with the case 4, the error is only about 0.31%. This shows that the new model is suitable for the drag reduction technology by HNPs.

In order to further verify the correctness of the model, the COMSOL multiphysic is used to simulate the fluid flow and the pressure distribution in the core displacement experiments. The simulation and the analysis of this technology are as follows.

Choosing a core (No. 1) from a block of one oil field with high injection pressure and low injection rate to simulate. The core parameters are shown in Table 1. The permeability measured with water is increased to 0.582×10–16/m2, the increase rate is 17%.

Table 2 comparison between experiments and different model’s simulations after hnps adsorbed

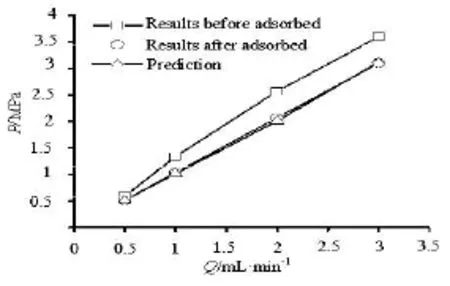
Fig.4 The relationship between pressure gradient and flow rate simulated with COMSOL

The relationship between the pressure gradient and the flow rate simulated with the COMSOL and experiments are shown in Fig.4. It is shown that after the HNP adsorption, the pressure measured with water decreases significantly, and the simulation results agree with the experimental results quiet well. In order to understand the pressure distribution, the variation of the displacement pressure under the injection rate of 3mL/min is also shown in Fig.5. It is obviously that the displacement pressure on the core is decreased from 3.596 MPa (Fig.4(a)) to 3.101 MPa (Fig.4(b)), and the pressure reduction reaches 13%.

Fig.5 The pressure distribution before/ after HNPs adsorption

6. Conclusions

(1) The seepage models of the common water flooding methods are usually based on the modified basic seepage models without consideration of the slip effect. In this paper, we establish a seepage model for the drag reduction technology by the HNP adsorption, which considers the slip effect in the micro-channel and the influence of the aperture reduction due to the HNP adsorption, based on the basic seepage models.

(2) The model enjoys a good prediction accuracy. The error between the model and experimental resultsis less than 2.5%. This results show that the proposed seepage model can reflect the intrinsic nature of the drag reduction technology by the HNP adsorptions.

(3) The pressure distribution under a given flow rate is obtained successfully with the model and the open function by the COMSOL, which effectively reflects the drag reduction by the HNP adsorptions.

[1] CHEN Z.Finite element methods and their applications[M]. Berlin, Heidelberg, Gemany: Springer, 2005.

[2] EWING R. E., WANG H. A Summary of numerical methods for time-dependent advection-dominated partial differential equations[J].Journal of Computational and Applied Mathematics,2001, 128(1-2): 423-445.

[3] ROSHANFEKR M., JOHNS R. and POPE G. Simulation of the effect of pressure and solution gas on oil recovery from surfactant/polymer floods[J].SPE Journal,2012, 17(3): 705-716.

[4] ZHAO Zi-gang. A method for defining condensate gas reservoir’s phase state characteristic and predicting gas well optimum output[J].Acta petrolei sinica,2001, 22(2): 49-55(in Chinese).

[5] ZHANG Ren-liang, DI Qin-feng and WANG Xin-liang. Numerical study of wall wettabilities and topography on drag reduction effect in micro-channel flow by lattice Boltzmann method[J].Journal of Hydrodynamics,2010, 22(3): 366-372.

[6] DI Qin-feng, SHEN Chen and WANG Zhang-hong et al. Experimental research on drag reduction of flow in micro channels of rocks using nano particle adsorption method[J].Acta Petrolei Sinica,2009, 30(1): 125-128(in Chinese).

[7] DI Qin-feng, GU Chun-yuan and WANG Xin-liang. Experimental investigation of drag reduction in micro-channels with surfaces adsorbed hydrophobic nanopar-ticles[C].Proceedings of the 9th International Conference on Hydrodynamics.Shanghai, China, 2010, 337-342.

[8] DI Q., SHEN C. and WANG Z. Innovative drag reduction of flow in rock[C].Proceedings of the International Oil and Gas Conference and Exhibition in China.Beijing, China, 2010.

[9] YIN X., PENG X. Numerical analyses of a spiral groove dry gas seal under slip flow conditions[C].Proceedings of the Seventeenth (2007) International Offshore and Polar Engineering Conference.Lisbon, Protugal, 2007.

[10] CLARKSON C. R., NOBAKHT M. Production analysis of tight-gas and shale-gas reservoirs using the dynamicslippage concept[J].SPE Journal,2012, 7(1): 230-242.

[11] BARRAT J. L., BOCQUET L. Large slip effect at a nonwetting fluid-solid interface[J].Physical Review Letters,1999, 82(23): 4671-4674.

[12] SHABRO V., TORRES-VERDIN C. and JAVADPOUR F. Numerical simulation of shale-gas production porescale modeling of slip-flow, knudsen diffusion, and langmuir desorption to reservoir modeling of compressible fluidC].North American Unconventional Gas Conference and Exhibition.The Woodlands, Texas, USA, 2011.

[13] YIN D., GAO P. and PU H. et al. Investigation of a new simulator for surfactant floods in low permeability reservoirs and its application in Chao-522 field, 2010 update[C].SPE128645.Muscat, Oman, 2010.

[14] WANG J., DONG M. Optimum effective viscosity of polymer solution for improving heavy oil recovery[J].Journal of Petroleum Science and Engineering,2009, 67(3-4): 155-158.

[15] YAO C. J., LEI G. L. and MA J. Y. Experiment and simulation of indigenous microbial enhanced oil recovery (IMEOR)[C].International Petroleum Technology Conference.Bangkok, Thaliand, 2011.

[16] CARMAN P. C. Fluid flow through granular beds[J].Transactions of the Institution of Chemical Engineeres,1937, 15: 150-166.

[17] ZHANG Ren-liang, DI Qin-feng and WANG Xin-liang. Numerical study of the relationship between apparent slip length and contact angle by lattice Boltzmann method[J].Journal of Hydrodynamics,2012, 24(4): 535-540.

10.1016/S1001-6058(13)60435-7

* Project supported by the National Natural Science Foundation of China (Grant No. 50874071), the Chinese National Programs for High Technology Research and Development (Grant No. SS2013AA061104 ), and the Shanghai Program for Innovative Research Team in Universities, Shanghai Leading Academic Discipline Project (Grant No. S30106).

Biography: GONG Wei (1988-), Female, Master

DI Qin-feng,

E-mail: qinfengd@sina.com