LLCL滤波的单相光伏并网逆变器控制技术研究

邱晓明，王明渝，胡文翠

（重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

随着传统能源的日益匮乏，开发和利用可再生能源迫在眉睫，其中，光伏并网发电是可再生能源的重要发展方向之一[1-2]。并网逆变器作为光伏并网发电系统的核心部件，一般须通过滤波器和电网相 连接，以阻止电流谐波进入电网，如何获得高质量的入网电流也是研究热点之一。

并网电流高次谐波主要集中在逆变器开关频率及其整数倍频率处。文献[3]提出了一种新型LLCL滤波器，通过在传统LCL 滤波器的电容支路中串联一个电感值较小的电感，和电容组成了一个串联谐振电路，其串联谐振频率设置在开关频率处，相比于LCL 滤波器更能够对开关频率处的电流谐波进行衰减，从而进一步减小总的电感值。和LCL 滤波器一样，LLCL 滤波器同样存在谐振问题，容易导致系统不稳定。目前抑制LCL 滤波器谐振的方法主要有无源阻尼法[4-5]和有源阻尼法[6-8]。分析表明，抑制LCL 谐振的控制策略同样适用于LLCL 滤波器。

本文采用了网侧电流外环，电感、电容串联谐振支路电流内环的双闭环有源阻尼控制来抑制LLCL 滤波器引起的谐振尖峰，增强系统稳定性。对于网侧电流外环采用带谐波补偿的准比例谐振(PR)控制器能够有效跟踪并网电流指令的同时，可针对特定次谐波进行补偿。但谐振控制器在其谐振频率处存在180°相角跳变，随着谐波补偿次数的增加，易导致系统不稳定。本文通过在带谐波补偿的准PR 控制器之后增加一个超前校正环节，利用该环节的相角超前对谐振控制器谐振频率处的相位进行补偿，同时提高了整个系统的相位裕量，从而增强了系统的稳定性。此外，为了减小电网电压畸变或扰动对系统并网电流的影响，系统中引入了电网电压前馈控制。

1 系统控制策略

基于LLCL 滤波的单相光伏并网逆变器基本结构如图1所示，忽略各电感和电容的等效串联电阻。

图1 LLCL滤波的单相光伏并网逆变器Fig.1 LLCL filter based single-phase PV grid-connected inverter

LLCL 滤波器通过在传统LCL 滤波器的电容支路中串联一个小电感，和电容一起组成了串联谐振电路，串联谐振频率由式(1)决定。

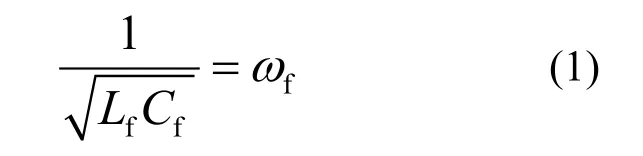
由图1 可求得LLCL 滤波器的等效模型如图2所示，得系统开环i2(s)/uAB(s)的传递函数如(2)所示。

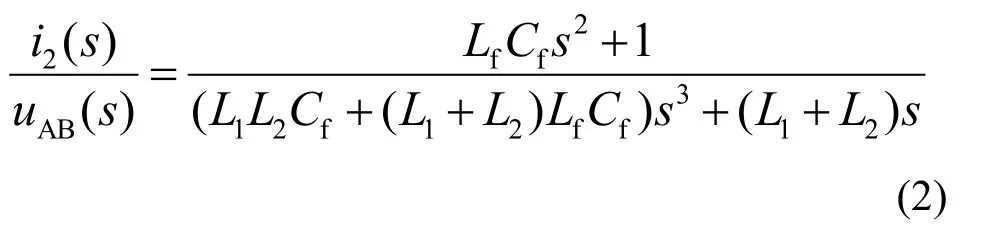
图2 LLCL滤波器等效模型Fig.2 Equivalent model of LLCL filter

画出系统开环i2(s)/uAB(s)波特图如图3所示，图中对比了采用LCL 滤波器时i2(s)/uAB(s)波特图，参数L1、L2、Cf相同。由图3 可以看出LLCL 滤波器在串联谐振频率处对高次谐波的衰减能力比LCL 滤波器要大得多，而在0.5 倍的串联谐振频率内其特性与LCL 滤波器相似，不足之处是在高于串联谐振频率段幅频特性以-20 dB/dec 衰减，对此频率段内的高次谐波衰减能力小于LCL 滤波器。因此当串联谐振频率设置在开关频率处时，可对并网电流开关频率处的高次谐波起到极大的衰减作用。

图3 采用LLCL和LCL时系统开环i2(s)/uAB(s)波特图对比Fig.3 Bode plots ofi2(s)/uAB(s) for LLCL and LCL filters

由图3 可知，采用LLCL 滤波器系统同样存在谐振尖峰问题，且增益在0 dB 之上，须要采取一定的措施抑制谐振尖峰，提高系统稳定性。抑制LCL谐振的无源或有源阻尼措施均适用于LLCL 滤波器。本文采取了网侧电流外环，串联谐振电路电流内环的双电流闭环有源阻尼策略[8]，同时为了减小电网电压畸变或扰动对并网电流的干扰，引入了电网电压前馈控制策略[9-10]，控制框图如图4所示。其中，igref为给定的参考电流信号，Gc(s)为网侧电流外环调节器，K为串联谐振电路电流内环比例调节器，K1为电网电压前馈系数，KSVM=1 为逆变桥等效比例环节，逆变器采用SVPWM 调制方式。

由图4可得电流环开环传递函数如式(3)所示，电流环开环传递函数特征方程阻尼系数ξ如式(4)所示。K取值越大，系统阻尼系数越大，抑制谐振的效果越好，但过大的系统阻尼会使系统动态性能变差，工程上一般取0.5<ξ<0.8。电流闭环传递函数如式(5)所示。由式(5)可看出采用电网电压前馈很难完全消除电网电压的干扰，可近似取K1=1/KKSVM。

图4 电流双闭环控制框图Fig.4 Block diagram of current dual-loop control strategy

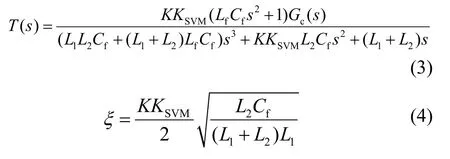
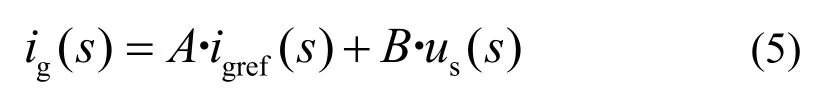
其中：

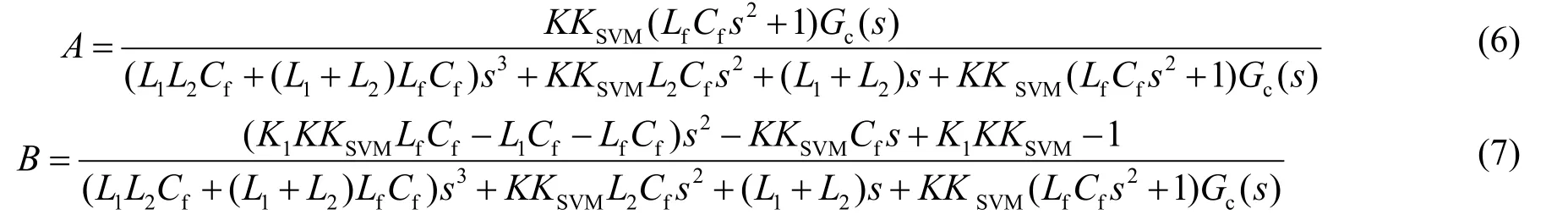
2 网侧电流外环控制设计

由第一节分析可知，采用电网电压前馈策略虽然可以一定程度上抑制电网电压的干扰，但不能完全消除其对并网电流的影响。网侧电流外环的目的是获得高质量的入网电流，带谐波补偿的准PR 控制器[11-14]不仅可以提高电流跟踪精度，实现单位功率因数并网，还可以抑制电网电压畸变引起的并网电流畸变。式(8)为带谐波补偿的准PR 控制器的传递函数，Kp为比例系数，Kr为谐振系数，ωc为带宽系数，ω0为基波角频率。波特图如图5所示，图中最高谐波补偿次数为11 次。

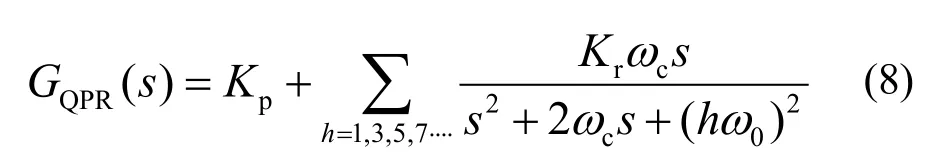
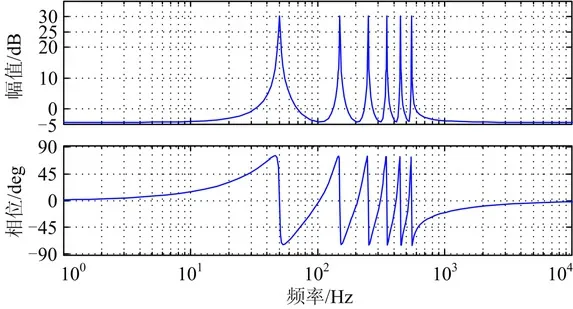
图5 带谐波补偿的准PR控制器波特图Fig.5 Bode plot of quasi PR with harmonic compensation

但谐振控制器在其谐振频率处存在约180°相角跳变，随着谐波补偿次数的增加，其与系统本身的相角延迟叠加后，容易导致系统在谐振频率附近发生-180°的相位穿越，使系统不稳定[13]。并且相位裕量也随着补偿次数的增加而恶化，因此谐波补偿一般只补偿3、5、7 次[14]。本文通过在准PR 控制器之后串联一个超前校正环节[15]，利用该环节的相角超前来提高谐振频率处的相位，可增加谐波补偿的次数的同时，增强了整个控制系统的相位裕量。

超前校正环节传递函数如式(9)所示。

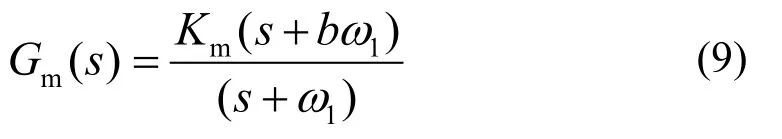
最大超前角与最大超前角频率分别如式(10)、(11)所示。

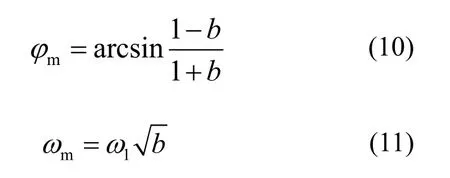
最大超前角频率ωm设置在补偿的最高谐波次数频率处，且最大超前角φm不宜过大，以免串联超前校正环节对系统整个开环传递函数幅频特性产生较大的影响，取10°<φm<30°。选取Km的原则可由Gm(s)在ωm处过0 dB 由式(9)计算所得。

本文中设计的最高谐波补偿次数为11 次，取最大超前角频率ωm定在11 次谐波频率550 Hz 处，最大超前角φm=20°，由式(9) ～式(11)可得Km=1.4，ω1=4 900，b=0.5。图6 为Gm(s)波特图，可以看出，在以ωm为中心的一定频率段内，Gm(s)都具有一定的相位补偿功能。

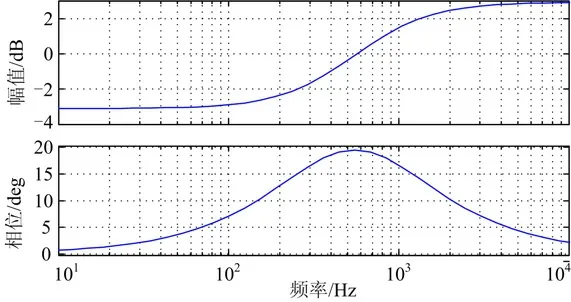
图6 Gm(s)波特图Fig.6 Bode plot ofGm(s)

因此，加入超前校正环节后网侧电流外环控制器Gc(s)传递函数如式(12)所示。

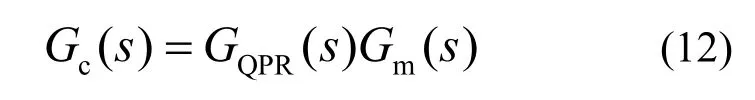
图7 对比了采用加入超前校正环节后，即式(12)所示的控制器与只采用带谐波补偿的准PR 控制器时电流环开环传递函数波特图。由图7 可以看出，加入超前校正环节后对系统的截止频率影响较小，却提高了系统在各谐振频率处的相位，且相位裕量从38.2°提高到56.2°，并且可看出超前校正环对系统整个频率域内的幅频特性影响较小，在基波频率及特定谐波补偿频率处仍有较大的增益。

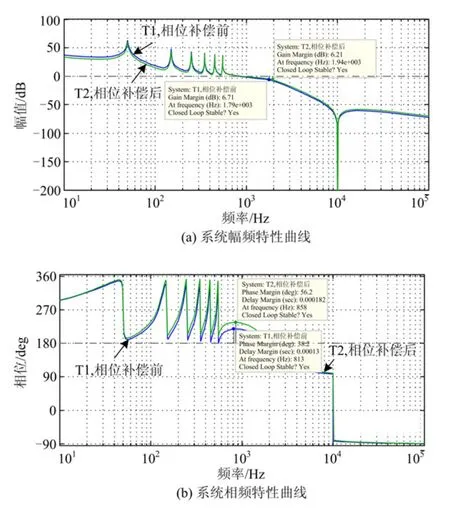
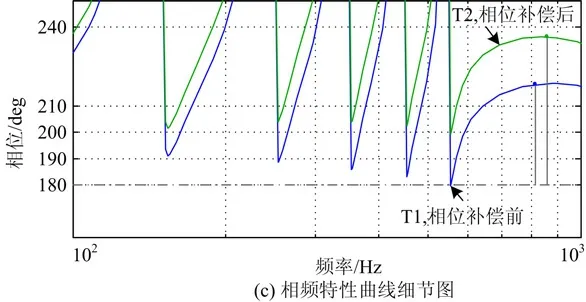
图7 电流环开环波特图Fig.7 Bode plot of current loop

3 仿真分析

为了验证理论分析的正确性，建立系统仿真模型，系统主要仿真参数如表1所示。表1 中，LLCL滤波器电容Cf按LCL 滤波器参数设计方法设计，则Lf由理论分析环节中式(1)可得，串联谐振频率为逆变器开关频率。带谐波补偿的准PR 控制器谐波补偿次数到11 次，KP=0.6，Kr=64，ωc=3.14，ω0=314。电流内环比例系数K=40。超前校正环节比例系数Km=1.4，ω1=4 900，b=0.5。

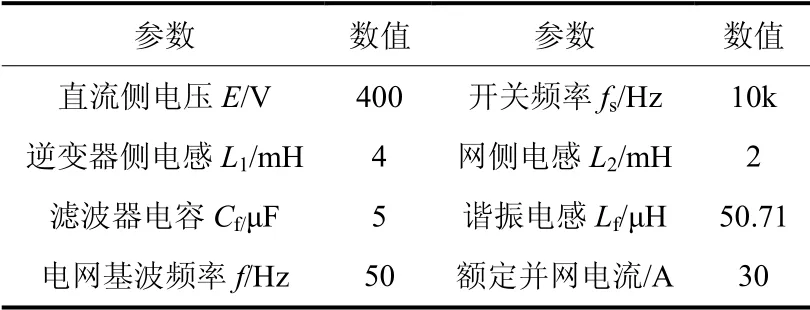
表1 系统仿真参数Table 1 System simulation parameters

仿真中，模拟电网电压含有3、5、7、9、11次谐波，谐波总畸变率THD=15.21%，图8 中给出了电网电压傅里叶分析。

图9 为并网逆变器仿真结果，并网电流在0.065 s 时幅值减半，电网电压在0.125 s 时突降。由图9可看出系统的动态性能良好，能够快速跟踪给定并网电流，并且具有良好的抗电网电压扰动性。

图10 为并网电流为额定值一半时的傅里叶分析。由图可知，即使电网电压含有较大的3、5、7、9、11 次谐波，系统仍能保证并网电流具有较低的THD 值。图11 为采用LCL 滤波时，并网电流傅里叶分析，对比图10 与图11 可知，LCL 滤波时并网电流高次谐波主要集中在开关频率附近，而LLCL滤波时并网电流开关频率附近的谐波得到极大的衰减，高次谐波集中在两倍的开关频率附近，且THD值小于LCL 滤波器。说明了LLCL 滤波效果优于LCL 滤波器。

为了验证串联超前校正环节对系统稳定性的影响，仿真中调节准PR 控制器参数Kp变化，其他参数均不变。当Kp=0.15，取值过小；或Kp=1.4，取值过大时，图12 为未加入串联超前校正环节的系统并网电流仿真波形，图13 为加入串联超前校正环节后系统并网电流仿真波形。对比图12 与图13 可知，加入串联超前校正环节后Kp的取值范围增大，增强了系统的稳定性。

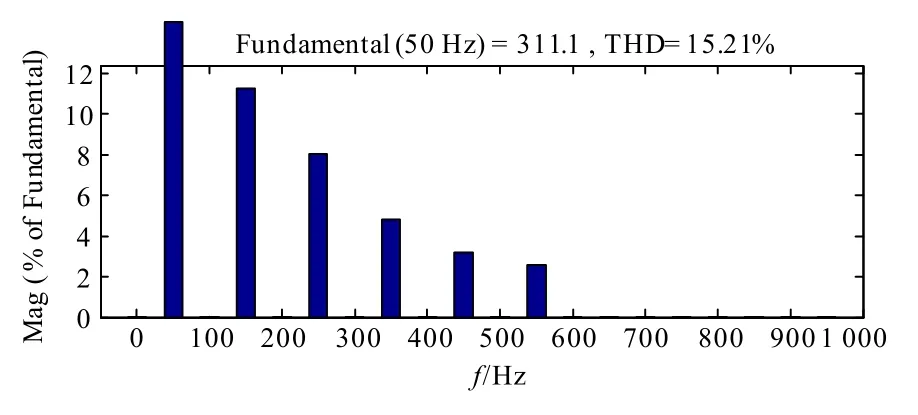
图8 电网电压傅里叶分析Fig.8 FFT of the grid-voltage

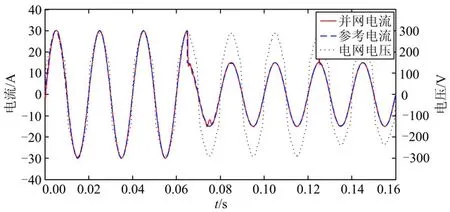
图9 并网逆变器仿真结果Fig.9 Simulation results of grid-connected inverter

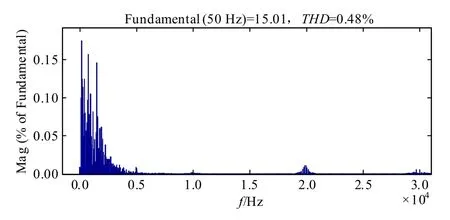
图10 并网电流傅里叶分析(LLCL)Fig.10 FFT of the grid current with LLCL filter

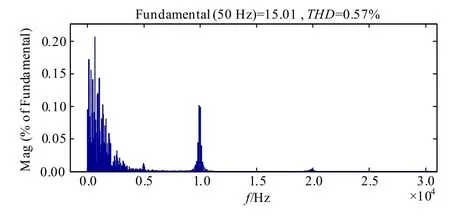
图11 LCL滤波时并网电流傅里叶分析Fig.11 FFT of the grid current with LCL filter

图12 未加串联超前校正环节仿真波形Fig.12 Simulation results with no series-leading correction

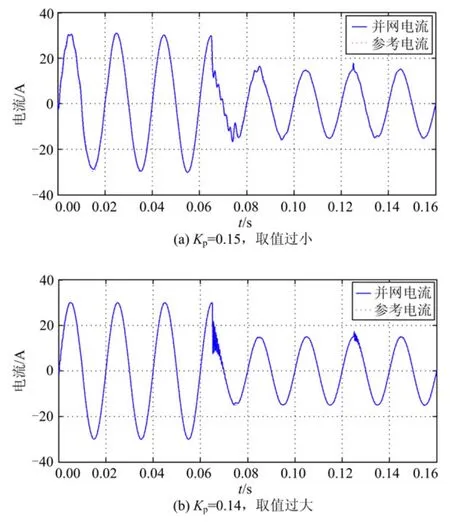
图13 加入串联超前校正环节后仿真波形Fig.13 Simulation results with series-leading correction

4 结论

本文采用LLCL 滤波器对单相光伏并网逆变器进行滤波，通过在开关频率处产生串联谐振，LLCL滤波器能够对开关频率处的并网电流高次谐波起到极大的衰减作用。采用并网电流外环，电感、电容

串联谐振电路电流内环的双闭环控制，提出在并网电流外环带谐波补偿的准比例谐振控制器之后增加一个超前校正环节，对谐振控制器谐振频率处的相位进行补偿的同时，提高了系统的相位裕量，增强了系统稳定性。引入电网电压前馈控制策略，增强系统对电网电压的抗干扰能力。仿真结果验证了理论分析的正确性和可行性。

[1]Bull S R.Renewable energy today and tomorrow[J].Proceedings of the IEEE,2001,89(8):1216-1226.

[2]周林,曾意,郭珂,等.具有电能质量调节功能的光伏并网系统研究进展[J].电力系统保护与控制,2012,40(9):137-145.

ZHOU Lin,ZENG Yi,GUO Ke,et al.Development of photovoltaic grid-connected system with power quality regulatory function[J].Power System Protection and Control,2012,40(9):137-145.

[3]WU Wei-ming,HE Yuan-bin,Blaabjerg F.An LLCL power filter for single-phase grid-tied inverter[J].IEEE Trans on Power Electronics,2012,27(2):782-789.

[4]张承慧,叶颖,陈阿莲,等.基于输出电流控制的光伏并网逆变电源[J].电工技术学报,2007,22(8):41-45.

ZHANG Cheng-hui,YE Yin,CHEN A-lian,et al.Research on grid-connected photovoltaic inverter based on output current control[J].Transactions of China Electrotechnical Society,2007,22(8):41-45.

[5]王小涛,曾成碧,刘晨曦.基于模糊控制的并网逆变器的研究[J].电力系统保护与控制,2011,39(9):97-101.WANG Xiao-tao,ZENG Cheng-bi,LIU Chen-xi.Study of grid-connected inverter based on fuzzy control[J].Power System Protection and Control,2011,39(9):97-101.

[6]Malinowshi M,Bernet S.A simple voltage senseless active damping scheme for three-phase PWM converters with an LCL filter[J].IEEE Trans on Industry Electronics,2008,55(4):1876-1880.

[7]彭双剑,罗安,荣飞,等.LCL 滤波器的单相光伏并网控制策略[J].中国电机工程学报,2011,31(21):17-24.

PENG Shuang-jian,LUO An,RONG Fei,et al.Single-phase photovoltaic grid-connected control strategy with LCL filter[J].Proceedings of the CSEE,2011,31(21):17-24.

[8]徐志英,许爱国,谢少军.采用LCL 滤波器的并网逆变器双闭环入网电流控制技术[J].中国电机工程学报,2009,29(27):36-41.

XU Zhi-ying,XU Ai-guo,XIE Shao-jun.Dual-loop grid current control technique for grid-connected inverter using an LCL filter[J].Proceedings of the CSEE,2009,29(27):36-41.

[9]Liserre M,Teodorescu R,Blaabjerg F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J].IEEE Trans on Power Electronics,2006,21(1):888-895.

[10]赵清林,郭小强,邬伟扬.单相逆变器并网控制技术研究[J].中国电机工程学报,2007,27(16):60-64.

ZHAO Qing-lin,GUO Xiao-qiang,WU Wei-yang.Research on control strategy for single-phase grid-connected inverter[J].Proceedings of the CSEE,2007,27(16):60-64.

[11]王玉斌,陈建良.基于LCL 滤波器的并网/独立双模式控制高性能逆变器设计[J].电力系统保护与控制,2010,38(20):110-114.

WANG Yu-bin,CHEN Jian-liang.High performance LCL-based utility-interactive design and parallel applications[J].Power System Protection and Control,2010,38(20):110-114.

[12]Liserre M,Teodorescu R.Multiple harmonics control for three-phase grid converter systems with the use of PI-RES current controller in a rotating frame[J].IEEE Trans on Power Electronics,2006,31(2):836-841.

[13]黄如海,谢少军.基于比例谐振调节器的逆变器双环控制策略研究[J].电工技术学报,2012,27(2):77-81.

HUANG Ru-hai,XIE Shao-jun.Double-loop digital control strategy based on proportional-resonant controller[J].Transactions of China Electrotechnical Society,2012,27(2):77-81.

[14]戴训江,晁勤,樊艳芳.基于阻尼谐振的光伏并网逆变器谐波补偿控制[J].电力自动化设备,2011,31(1):79-83.

DAI Xun-jiang,CHAO Qin,FAN Yan-fang.Harmonic compensation control of grid-connected inverter based on damping resonance[J].Electric Power Automation Equipment,2011,31(1):79-83.

[15]左为恒,周林.自动控制理论基础[M].北京:机械工业出版社,2007:149-150.