两系统链视角下科技协同创新效率研究——基于我国28省市高技术产业的数据分析

□冯 锋 燕会雷 [中国科学技术大学 合肥 230026]

引言

高技术产业对我国经济发展起着非常重要的作用，为了争取在激烈的市场竞争中占据有利地位，各省市都加大了对高技术产业的科技投入。科技创新在促进经济的发展中占据着主导地位[1]，企业自身竞争力的高低不仅取决于科技投入的多少，更取决于其效率的高低[2]。因此本文对我国各省市高技术产业投入产出效率的研究就显得具有较强的现实意义。

目前，对科技投入产出效率的研究方法主要包括数据包络分析、相关指标法等。由于数据包络分析方法能够对科技投入的多个指标进行衡量，因而应用最为广泛，如用于资源城市发展效率等[3]。通过使用DEA方法对我国区域R&D投入产出水平进行研究，谢建国发现我国30个省市的科技投入产出的技术有效性较高，而经济有效性偏低[4]；基于阿尔蒙法的滞后期模型,胡振华、刘笃池从科技投入规模和投入产出效率出发，对我国30 个省市1996～2006年的科技投入进行研究[5]；刘民婷、孙卫运用DEA方法对陕西省的产学研合作效率进行了实证分析，得出行业的不规模和对科技投入产出效率的不重视是导致陕西省制造业产学研合作效率不高的主要原因[6]；以DEA方法为基础，章仁俊、王俊峰对我国1992～2007年的36个工业企业自主创新效率进行了研究分析，得出二次创新效率是自主创新效率的主要原动力[7]。

本文以高技术产业的科技投入产出作为研究对象。OECD认为高技术产业的生产包括技术研发、改造以及应用等过程，从投入到产出中间需要经历一系列过程，故成果的应用具有一定的时间滞后性[8]。高技术产业的投入产出分为技术产出和技术转化两个阶段，考虑到投入产出的转化时滞，根据庞瑞芝[9]等的实证研究，本文把阶段时间的滞后性作一年处理。因此，高技术产业的科技投入产出分为技术生产和技术改造与应用两个阶段。考虑到投入产出的滞后性，本文通过两阶段模型对我国28省市的高技术产业的2008、2009、2010年的科技投入产出数据进行效率研究。

一、研究方法概述

（一）灰色关联度分析概述

灰色关联度通过因子间的影响程度或各因子对目标值的贡献测度来寻求系统中各子系统(或因素)与目标值之间的关系，灰色关联度越大说明子因素对目标值的贡献就越大，反之越小。具体计算如下：

假设原始数列为M0(x)={m0(1),m0(2),...,m0(q)}，比较数列为Ni(x)={ni(1),ni(2),...,ni(q)}，i=1,2,...,u，x=1,2,...,q。其中u表示比较列个数，n为样本数；则M0(x)与Ni(x)之间的关联系数为：

上式中，λ为系数（0＜λ＜1），分辨系数根据本文研究需要，定为0.5。

综上，则有M0和Ni之间的关联度为：

（二）链式DEA模型的建立

A .Charnes,W.W.Cooper和E.Rhodes于1978年提出了数据包络分析( Data Envelopment Analysis,简称DEA)[10]，该方法可以被广泛应用于评价一组同质的决策单元之间的相对效率[11]。传统的DEA得不出生产过程的中间阶段的效率及各阶段对生产过程的整体效率的影响情况，而链式网络DEA模型不仅可以决策单元的整体有效性，也可以评价决策单元各阶段的有效性，找出问题的症结[12]。

本文运用的DEA模型是两阶段系统模型，如下图1所示。下图中N1是子决策单元Q的输入向量，N1∈ENQ；M1不仅是子决策单元S的输入向量，同时也是子决策单元Q的输出向量，称其为中间向量，M1∈EQS；在二阶段中N2是子决策单元S的输入向量，I2∈ENS；M2是子决策单元S的输出变量，M2∈EMS。在该链式系统中，假设各个子决策单元在各自的生产前沿面上都有锥性投影，因此可以利用C2R模型对每个子决策单元的效率进行评价。在该模型中，只考虑决策单元等产出前沿面上的锥性投入投影；则子决策单元Q和S的两个虚拟子决策单元（或称投影）就构成一个虚拟的链式模型系统。

图1 系统链式DEA系统模型

综上所述，子决策单元Q的投影是输入尽可能小但是中间向量保持不变，而子决策单元S的投影则是输出尽可能大而且中间向量不变，其中中间向量均保持变化。因此链式系统模型生产可能集是由所有实际的和虚拟的链式系统所组成，记作Y，则Y的表达式为：

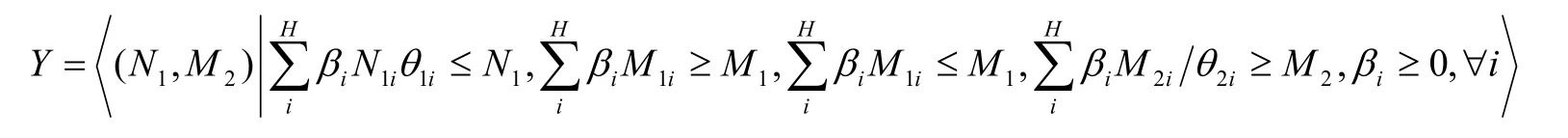
上式中，H表示决策单元数，投入或产出的乘数用β表示，C2R效率值用θ表示。在可能集Y下，链式系统模型的效率可用如下线性规划问题表示：

其中α0为目标函数值，st为约束条件，B和K分别表示投入和产出权重[13]。

（三）检验模型的建立

本文采用单一因子回归建模，将整体效率作为因变量，证以上结论即两阶段的协同创新对创新效率具有正向作用。建模如下：

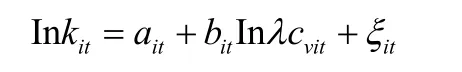
其中，Kit表示i各省市t年的创新效率水平，cλvit表示i省市t年的科技创新系统中两子系统的协同创新水平，ait、bit为待估参数，ξit为随机误差项。

两子系统的协同创新水平表示二者协同创新的拟合度，二者拟合度越高表示二者的协同创新水平越高。本文将通过协同模型来检测两子系统的协同创新的拟合度，各省市创新系统中的协同创新水平可以用其相对离差cλv表示。其表达式如下：

其中，M1和M2分别表示两子系统的创新水平，n为分辨系数，且n≥2，0≤vCλ≤1。

二、段科技投入产出链模型建构和指标 遴选

在科技投入产出两阶段链中，企业的研发机构是科学技术生产的主要机构，而申请的专利和新产品项目数是第一阶段的产出，企业的专利、新产品项目数和技术的消化和吸收等则是技术的改造与应用阶段的投入，新产品产值和销售收入则是最终 产出。

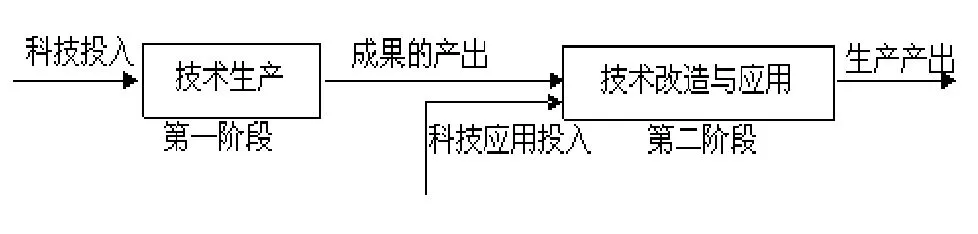
图2 两阶段链科技投入产出模型

如图2，技术生产属于第一阶段，技术改造与应用属于第二阶段。在第二阶段，企业不但吸收第一阶段的科技成果作为自身的投入，同时，也会相应投入资源。最终产出为新产品产值和新产品销售收入。上述模型中，共包括科技投入、科技成果产出、科技应用投入和生产产出等四个指标。本文根据已有研究[14～16]际情况对各个指标进行了细化，形成了可衡量且符合实际的指标体系。其中：

科技投入指标包括企业科学家与工程师（人）、R&D人员折合全时当量（人年）、科技活动经费内部支出（万元）、R&D经费内部支出额（万元）等4个细化指标。

科技成果产出指标包括专利授权数（个）、新产品项目数等2个细化指标。

科技应用投入指标包括专利授权数、新产品项目数、技术吸收消化费用（万元）、技术应用和改造经费（万元）、新产品开发经费支出（万元）等5个细化指标。

产业产出指标包括新产品销售收入、新产品总产值等2个细化指标。

综上，把科技投入、科技成果产出和科技应用投入、生产产出的数据分别使用第t年、第t+1年、第t+2年的数据。具体而言，科技投入指标采用2008年的数据，科技成果产出和科技应用投入指标采用2009年的数据，而最终产出数据则采用2010年的数据。本文选取我国28个省市（新疆、西藏和青海部分数据缺失）的高技术产业作为决策单元，数据均来源于《中国科技统计年鉴》和科技部网站等。

三、实证分析

（一）科技投入要素与产出结果的灰色关联度分析

分别用w1、w2、w3、w4、w5、w6、w7、w8、w9表示第t年各省市高技术产业投入的科学家与工程师（人）、R&D人员折合全时当量（人年）、R&D经费内部支出额（万元）、科技活动经费内部支出（万元）和第t+1年的投入的新产品开发经费支出（万元）、专利授权数、新产品项目数、技术吸收消化费用（万元）、技术应用和改造经费（万元）等，各要素前一年的投入与第二年的产出灰色关联度的计算结果如下表：

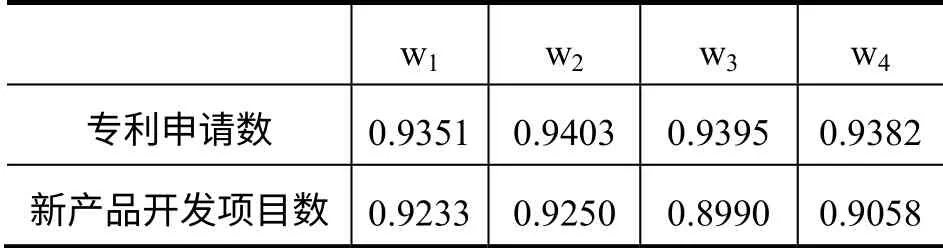
表1 第一阶段投入产出的灰色关联度

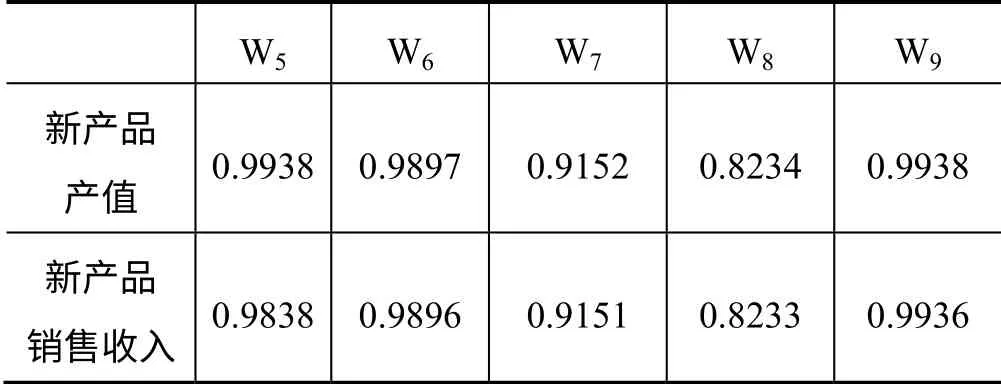
表2 第二阶段投入产出的灰色关联度

从表1和表2的灰色关联度中可以看出，本文对于阶段链所选取的投入产出指标之间有着非常高的关联度，因此，可以用链式DEA模型进行测算各省市的分阶段和整体阶段效率。

（二）数据处理结果

基于上面所示的链式网络DEA系统模型的特征，本文在对我国28个省市的的科技投入产出两阶段效率进行分析时借助Matlab软件，对两个分阶段效率的计算使用了C2R进行计算，结果如表3所示。

为了便于比较各省市各个阶段和综合效率，把我国28省市的分阶段效率和两阶段综合效率绘制在企业-效率图中，可以直观地看到各阶段的效率走势图，如图3所示。

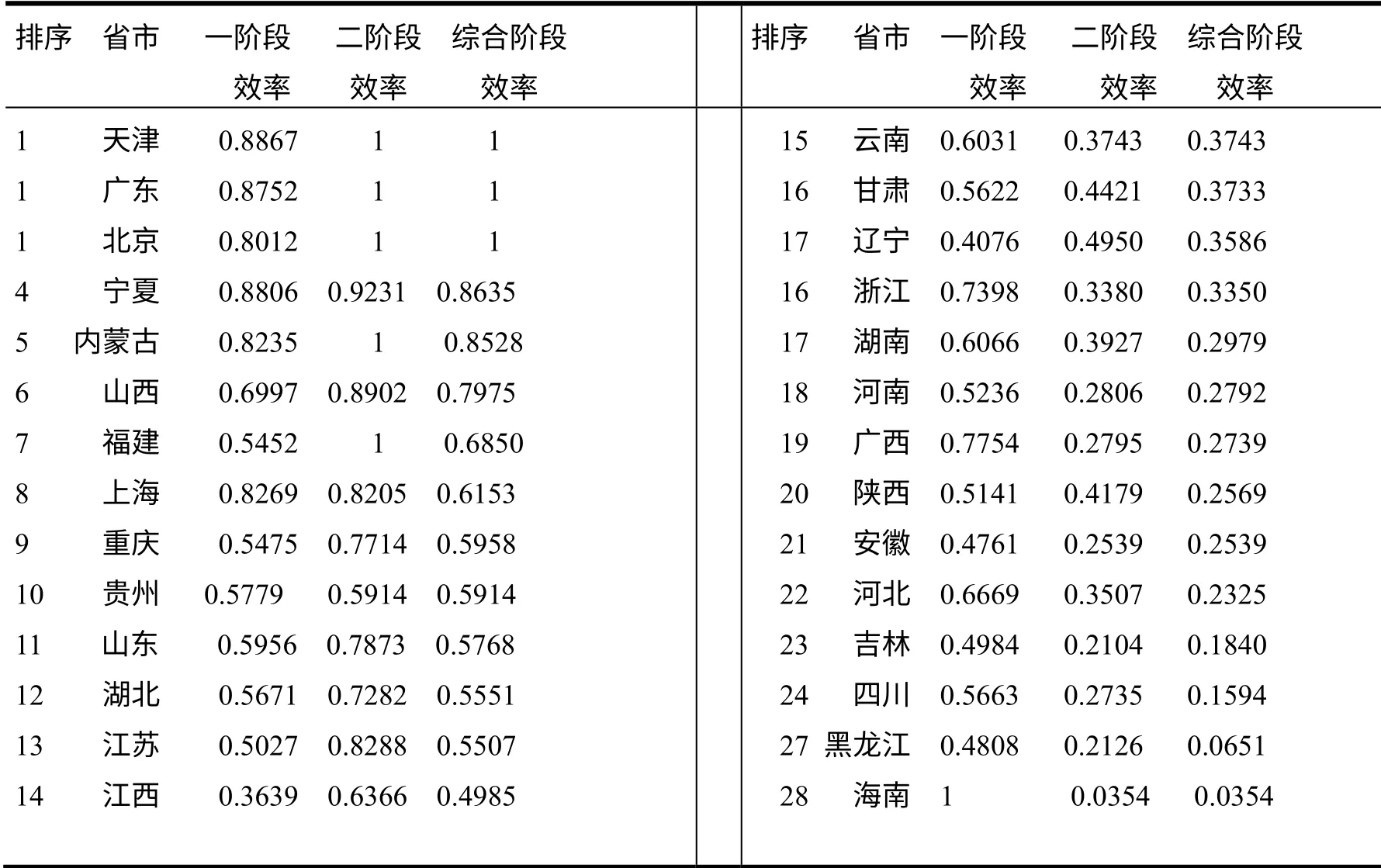
表3 各省市两阶段科技投入产出链效率

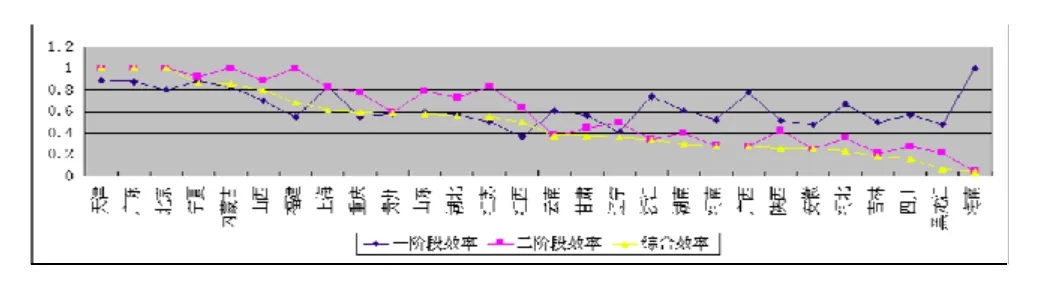
图3 我国各各省市投入产出效率图

（三）模型检验分析

借助上面模型对各省市的科技投入产出阶段效率和整体效率协同创新水平进行测算。采用包含单位根的截面加权估计法（CSW）对模型进行估计。模型回归结果详见下表。

表4 模型回归结果

从表4中看出，在0.05的显著水平下，回归系数b通过了显著性检验。因此两子系统的协同创新水平对整体科技创新系统效率具有明显的正向影响。

（四）数据处理结果分析

从以上表格和图形中我们可以看出在综合阶段上，我国各省市效率有着很大差别。其中天津、广东、北京的综合阶段效率最高，其值为1；而宁夏和内蒙古效率也较高，其值为都在0.8以上。综合阶段效率在0.5以上的，有福建、上海和江苏等8省市，而江西等省市效率都在0.5以下；其中黑龙江和海南整体效率最差，其值不足0.01。

在我国28省市高技术产业投入产出效率中，各阶段的产出效率也有着很大差别。在一阶段产出效率中，天津、广东、宁夏等的效率最优，其值均在0.8以上；一阶段效率值在0.6以上的有山西、海南等7省市，其中海南省一阶段的效率更是高达1；一阶段效率值在0.6以下的有重庆、陕西等省市，其中江西效率最低。在二阶段产出效率中，广东、北京、等省市效率最优，其值为1；效率值在0.8以上的有宁夏、江苏等4省市；效率值在0.6以上的有重庆、江西等，其余的二阶段效率则在0.6以下，而海南的效率最低。

（五）相似性分析

为了找出投入产出规律以提高各省市投入产出水平，本文使用SPSS统计软件运用聚类分析的方法对各省市两阶段科技投入产出链的效率进行相似性研究，聚类结果如图4所示。

从图4中不难看出，根据投入产修护效率把我国的28个省市分为四类。第一类为广东、上海和福建等，这些省市两阶段和综合阶段效率很优，称之为效率兼优型省；第二类为云南、河北和广西等，这些省份在技术生产阶段效率较优，而技术转化为生产能力的效率较低，称之为技术生产效率偏优型省市；第三类为重庆、江苏和江西等省市，这些省市将技术转化为生产力的效率较高，但科学技术的生产阶段效率不高，称之为技术的改造与应用效率偏优型企业；第四类为甘肃、辽宁、黑龙江等省市，这类省市科学技术的生产与应用阶段的效率都不高，导致整体效率也不高，称之为效率兼劣型省。

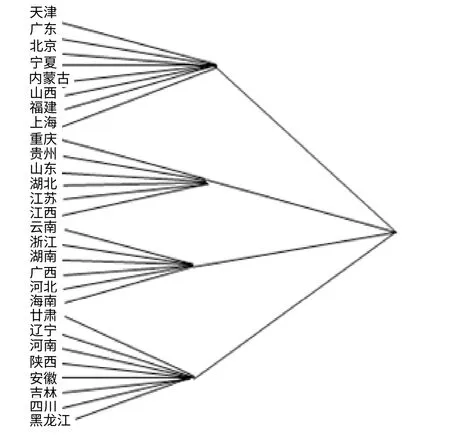
图4 各省市效率相似性分析

（六）效率图谱分析

根据以上的聚类分析，本文绘制出了我国各省市高技术产业投入产出的效率图谱，如图5所示，这样更能清楚地看出我国各省市高技术产业一阶段、二阶段和综合阶段效率的分布情况，便于我国在制定政策时从宏观上进行把握。

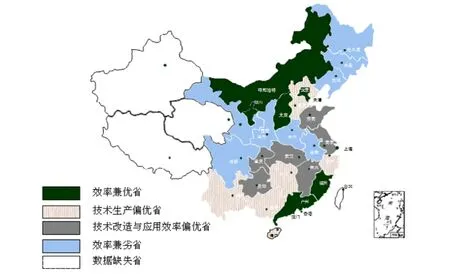
图5 各省市科技投入产出效率图谱

四、结论及建议

本文通过链式DEA系统模型对我国28省市进行了科技投入产出的分阶段和整体效率研究，并把其分为四类，即效率兼优型省市、技术生产偏优型省市、技术改造与应用偏优型省市和效率兼劣型省市四类。

根据以上结论，提出以下建议：

1．各省市在进行科技投入时，不能忽视各个靶阶段的效率，应充分把握投入产出的阶段性特点，重点针对效率改进的靶阶段，做到有的放矢，努力提高靶阶段的效率。在技术生产方面效率不高的省市如重庆、山东等，应加大对基础技术生产的投入。对于湖南、河北和广西等技术的改造与应用阶段效率不高的省份，要加大对技术的改造，努力提高技术转化为实际生产力的能力。对于效率兼劣型的省市如甘肃、陕西等，两子阶段的效率都要提高，才能提高整体阶段的效率。

2．中央政府在对各地区进行财政拨款和制定各种优惠政策时，要有目的性的政策倾斜，根据不同类型的地区有所侧重，以提高不同省市的不同阶段的效率；同时国家可以根据我国八大区域的划分，有针对性地设立高技术产业区，使之有利于从整体上提高各阶段的效率。

总之，本文把灰色关联度、链式DEA模型和单因子回归模型结合起来，对我国高技术产业进行研究，为今后研究区域科技投入产出效率提供了独特的视角。由于链式DEA模型的方法有着一定的局限性，只注重数据而忽视了各省市经济的发展水平等。因此，在以后的研究中，可以与地区的经济发展水平相结合，使其更加具有理论和现实意义。

[1]GRILICHES Z.Productivity,R&D,and basic research at the firm level in the 1970,s[J].American Economic Review,1986(1):141-154.

[2]吕喜英.基于DEA的我国科技投入产出二次绩效评价[J].广西财经学院学报，2009,22(3):47-52.

[3]傅利平,王中亚.基于DEA模型的资源型城市经济发展效率实证研究[J].电子科技大学学报，2010(6):20-23.

[4]谢建国，周露昭.中国区域技术创新绩效——一个基于DEA的两阶段研究[J].学习与实践,2007(6):29-34.

[5]胡振华,刘笃池.我国区域科技投入促进经济增长绩效评价[J].中国软科学,2009(8):94-97.

[6]刘民婷,孙卫.基于DEA方法的产学研合作效率评价研究[J].科学学与科学技术管理,2011,32(03):12-15.

[7]章仁俊,王俊峰.中国工业企业自主创新效率评价：基于DEA 方法的研究[J].中国科技论坛，2010(05):52-56.

[8]陈爱国,魏晓平.技术产业科技活动效率：基于CCA-DEA的分析[J].科技进步与对策,2010,27(24):113-115.

[9]庞瑞芝,李鹏.中国工业创新：过程、效率与模式[J].产业经济研究,2011(02):3-4.

[10]CHARNES A,COOPER W W,RHODES E.Measu ring the efficiency of decision making uni ts [J].European Journal of Operat ion al Res earch,1978,2(6) :429-444.

[11]魏权龄.评价相对有效性的DEA方法[M].北京:中国人民大学出版社,1988.

[12]魏权龄,庞立永.链式网络DEA 模型[J].数学的实践与认识,2010,40(01):213-215.

[13]杨锋,翟笃俊,樑梁,毕功兵.两阶段链系统生产可能集与DEA评价模型[J].系统工程学报,2010,25(3):401-406.

[14]梅桥.基于DEA的科技投入产出分析与政策研究——以我国东部11省市为例[D].合肥:安徽大学,2010.

[15]邵一兵,孙熠.两阶段DEA模型在可持续发展评价中的应用[J].技术经济与管理研究,2006,60:35-36.

[16]谢友才,张红辉.区域科技投入产出效率的DEA视窗分析[J].研究与发展管理,2007,19(3):85-92.