考虑孔压消散时黏土的动变形研究
郑 刚,霍海峰,雷华阳,张立明(1. 天津大学水利工程仿真与安全国家重点实验室,天津 30007;. 天津大学滨海土木工程结构与安全教育部重点实验室,天津 30007)
考虑孔压消散时黏土的动变形研究
郑 刚1,2,霍海峰1,2,雷华阳1,2,张立明1,2
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 天津大学滨海土木工程结构与安全教育部重点实验室,天津 300072)
针对饱和黏土随时间的增加不断排水的情况,在不排水动剪切之后,实施了孔压消散阶段,并对不同消散程度土体的不排水剪切变形进行了研究.结果表明:完全固结后,饱和黏土刚度与动强度将会提高,再次保持原动应力水平不排水剪切时,土体轴向塑性变形基本不发生变化;当孔压消散与不排水动力剪切重复作用时,土体的变形主要来自于固结排水产生的轴向形变,且动剪切产生的动孔压与固结时的排水量随固结次数的增加而减小,并最终趋于稳定.随着固结度的增加,不排水剪切时的动变形不断减小.
动变形;动孔压;固结;不排水剪切
近些年,国内沿海地区修建了大量的公路、铁路等交通干线,在这些基础设施服役期间,路基在长期交通荷载作用下的变形量是相当可观的.资料显示,上海一号线运营后某段沉降量达到了20,mm左右[1];日本道路协会对低路基软土地基进行实测[2],发现服役期间地基沉降量约为建设期间的一半;Miura等[3]通过实测发现Saga机场道路开放交通后的附加沉降达到15,cm左右.
为揭示工后路基沉降机理并预测运营期间沉降量,国内外众多学者针对不同影响因素做了许多定性定量研究,如Monismith等[4]提出了简单的指数模型,将土体累积轴向变形与循环振次建立了联系;Chai等[5]通过引入静偏应力对此指数模型进行了修正;Hyodo等[6]针对高塑性海积黏土,采用经验模型模拟循环荷载作用下软黏土的孔压消散过程;周健等[7]将动力荷载引起的沉降分为瞬时沉降和固结沉降,并建立了残余应变公式;张茹等[8]研究了振动频率对于饱和黏土变形的影响;蔡英等[9]则建议采用半对数方程来建立累积塑性应变与循环周数的关系.
已有的对于饱和黏土变形预测经验公式大多是直接建立其与循环振次的函数,在此基础上综合考虑各种因素的影响,例如,将荷载简化为连续作用的循环荷载,并在此条件下进行剪切.因认为黏土的渗透系数较小,交通荷载作用下产生的动孔压来不及消散,故已进行的试验一般将饱和黏土的变形发展看做不排水状态.而现实中,动荷载作用下饱和黏土并非完全不排水,且车辆荷载等产生的循环荷载常常是有间歇期的(例如地铁夜间不运营),这会使孔压得到部分消散,土体得到一定程度的固结压密,从而又会影响到下一阶段动变形发展.因此,在考虑孔压消散情况下,研究土体的累积轴向变形规律,对揭示长期交通荷载作用下路基的变形机理具有重要的现实意义.
笔者通过一系列室内动力试验,研究了循环荷载作用下饱和黏土的动变形特性,着重探讨了考虑孔压消散对其变形的影响.
1 试验土样与试验步骤
1.1 试验土样
试验中的黏土取自天津临港工业区,深度9~11,m,主要有3类土,分别为可塑黏土、软塑黏土、粉质黏土.具体物理指标如表1所示.

表1 主要物理参数Tab.1 Major physical parameters
1.2 试验步骤
试验设备采用英国GDS动态三轴仪,竖向激振力为电磁式控制,振动频率最大可达5,Hz,孔压传感器安置在土样底部.
交通荷载引起的应力波是一种低频率、低动应力的单向脉冲波,故试验中对于动荷载的模拟采用具有静偏应力的正弦荷载,频率选用1,Hz.试验步骤具体如下.
步骤1 土样制备:按规范要求制取原状样,直径39.1,mm,高80,mm,并进行抽真空饱和,若饱和度达不到要求,则反压饱和至满足要求.
步骤2 土样固结:水位线在地下1,m左右,故对深度10,m左右的土取有效围压σ3,=100,kPa,并进行等向固结,固结过程中,给试样施加一个相对围压很小且恒定的偏应力以保持顶帽与试样接触,固结完成以孔压降至反压为标准.
步骤3 施加一定的偏应力qs,此阶段不排水,并以此偏应力作为动应力幅值进行不排水循环剪切,振动一定次数后,主要为500次、1,000次、2,000次,产生动应变εd,动孔压u1,2个指标均为动应力在平衡位置所测.
步骤4 将主应力差降为0,并进行排水固结,超孔压消散为u′1,排水量为v1.
定义固结度Up=1-u′/u,当试验不研究固结度对动变形影响时,均使动孔压降为0,即完全固结.
步骤5 重复步骤3与步骤4,动孔压和排水量分别为u2,v2,…,un,vn.试验中主应力差随时间变化如图1所示.

图1 主应力差与时间关系Fig.1 Relationship between deviatoric stress and time
2 试验结果分析
2.1 孔压消散对土体变形与强度的影响
为研究孔压消散对土体变形与强度的影响,笔者对可塑黏土、软塑黏土、粉质黏土做了相应的试验,分别研究了在不同动应力比r、不同循环振次N作用下,固结后土样的动力变形情况,其中,动应力比r= σd/(2σ3),σd为动应力振幅,σ3为固结围压,具体结果如图2所示.ε1为当动应力达到平衡位置时土样的轴向塑性应变.图中曲线上升部分为黏土的不排水循环剪切阶段,在转折处停止剪切进行排水固结,孔压消散完全后,继续不排水动力剪切,为方便对固结前后动力剪切变形进行比较,图中忽略了由固结引起的应变.可以看出,不论是对可塑黏土、软塑黏土,还是粉质黏土,孔压消散后继续振动时,其变形不再发生变化,说明土样刚度有较大水平的提高,为进一步了解孔压消散对其变形的影响,本文针对试验中的可塑黏土做了更加细致的研究.
图3为考虑孔压消散轴向变形曲线.其中虚线部分为动应力比0.200情况下,不考虑孔压消散的轴向变形,可以看出变形曲线属于破坏型,在振次4,000次左右出现转折.若在振次分别为500、2,000、5,000时,停止振动并进行排水固结,动孔压完全消散后,继续按原动应力水平振动,产生累计塑性应变曲线如实线所示,其中OA段为孔压消散过程中轴向变形的增加,AB段为固结之后不排水循环剪切,可以看出孔压消散后土样刚度有较大提高,振动期间变形基本不发生变化.
图4中第1阶段为动应力比0.175下不排水剪切土样的轴向变形,第2阶段为孔压完全消散后保持动应力比0.175不变不排水剪切,此阶段轴向应变不再发生变化,当动应力比提高到0.250后,变形才继续发展,但增加幅度仍小于第2阶段,说明孔压消散后土体的动强度将有较大程度的提高.
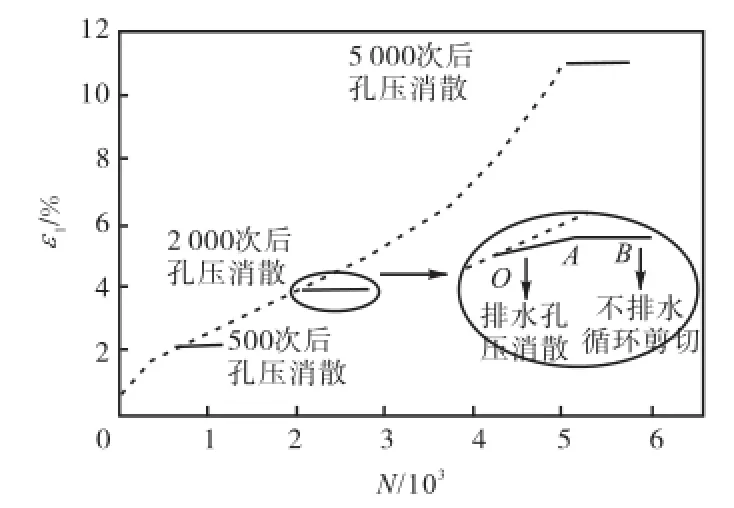
图3 考虑孔压消散轴向变形曲线Fig.3 Axial deformation of clay with consideration of pore dissipation of pressure

图4 孔压消散后不同动应力比下变形曲线Fig.4 Dynamic deformation of clay under different dynamic loading ratio with consideration of dissipation of pore pressure
黄茂松等[10]认为,结构性黏土在动荷载作用后由于土体结构的破坏,有效围压的降低,黏土的不排水强度与刚度会有所下降.而本文试验中,孔压消散后,其刚度与强度均有一定的提高,这主要是由于孔压消散过程中,土中水的排出对于土体属于固结压密过程,当此压密作用对土样的影响大于结构性破坏产生的影响时,土样强度与刚度将有所提高,反之则下降.
2.2 孔压消散固结度的影响

图5 不同固结度下的轴向应变Fig.5 Axial strain under different consolidation degrees
图5 为不同固结度下土样的轴向应变.试验土样首先在动孔压比0.200下振动500次,产生超孔压u,再按不同固结度进行排水固结,固结度如试验步骤4中所定义,孔压消散为u′,之后保持原动应力水平不排水再振动500次.试验中,孔压传感器与土样底部相连,可通过监测孔压值的变化来控制土样的固结度.由于不同固结度下,由固结引起的土样变形有所不同,即图3中的OA段.为方便比较,数据处理时均忽略固结过程中的变形量.
由图5可以看出,随着固结度的增加,动剪切时土样变形会减小,当固结度达到60%时,轴向应变增加很有限,固结度达到100%时,轴向应变不再发生变化.
图6中NCL为饱和黏土的正常固结线(normal consolidation line)[11].本次试验中土样先在围压下固结,孔隙比e1,土样在交通荷载作用下不排水振动,状态由A点变为B点,之后随着孔压的消散,土中水不断排出,完全固结时土体状态位于C点,孔隙比降为e2,在NCL中,孔隙比e2对应的固结压力为,故C点的土体处于似超固结状态.
对于交通荷载作用下的结构性黏土,存在一个门槛动应力比r′,如果所施加的动应力比小于此门槛,土体将不产生轴向塑性应变[12].当门槛动应力比一定时,孔压完全消散后C点的门槛动应力为2,将大于A点门槛动应力2,若原动应力水平低于2,土体动应变将不再发生变化.故试验中,完全固结后剪切时,动应变不再增加.

图6 e-ln p′平面上状态路径Fig.6 State path in the e-ln p′ plane
2.3 重复消散剪切下的变形
循环荷载作用下路基的沉降主要分2类,第1类为动荷载直接作用下,路基产生的瞬时沉降;第2类为动孔压消散过程中,由于土中水的排出,土体固结产生的变形,现实中路基的沉降是上述二者的综合作用.因此,在施工期与运营期不同阶段,区分构成沉降的主因与次因成为准确预测路基沉降的关键.笔者假设交通荷载作用是由剪切与固结循环构成,且每组循环中固结时动孔压完全消散,并进行了一系列试验研究,主应力差与时间关系如图1所示.
图7为动应力比0.200,每组循环2,000次,重复剪切固结作用下土样的轴向应变曲线.可以看出,第1次孔压消散后,在保持原动应力水平情况下,黏土的变形主要由孔压消散来决定,不排水循环剪切过程中,瞬时变形基本不发生变化;第1次固结引起的轴向应变为0.35%,且随着孔压消散次数的增加,每次消散过程中土样固结变形不断减小,经过多次消散后,固结总变形不足1%,其值远小于未固结时动荷载引起的变形.
在图7的试验结果中,OA段为孔压消散阶段,ABC为不排水循环剪切阶段,可以看出固结变形在A点出现峰值,剪切时变形稍有下降并趋于平稳.BC低于A点的原因是,曲线中各点为作用一个循环后当动应力达到平衡位置时所取,而动应变关于时间的曲线与动应力相似为正弦函数,考虑到黏土的滞后性,即动应变相对于动应力的出现有所滞后,当动应力取平衡位置时,所取的动应变会较实际的应变平衡位置有所减小,表现为BC较A点稍有降低.

图7 重复剪切固结下轴向变形曲线Fig.7 Axial deformation of clay under the repeated dissipation and shear
图8 为每组循环荷载剪切时动孔压比发展曲线.可以看出,孔压发展呈双曲线型,初始阶段发展较快,之后增速放缓,并最终稳定.当振动次数一定时,随着固结次数的增加,动孔压比不断减小.
图9为每组循环荷载剪切后产生的动孔压比随固结次数的变化.随着固结次数的增加,土样不断地排水压密,每组循环荷载剪切后产生的动孔压比将先减小,之后有稳定的趋势.
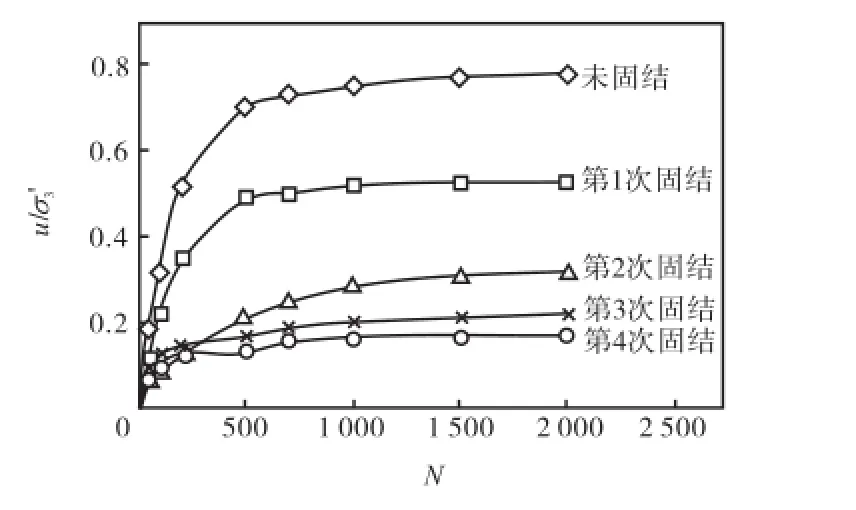
图8 动孔压比发展曲线Fig.8 Curves of dynamic pore pressure ratio

图9 动孔压比随固结次数变化Fig.9 Relationship between dynamic pore pressure ratio and consolidation times
图10 为每组循环荷载产生的孔压完全消散时土样的排水量.固结排水量的发展与孔压的发展趋势相同,均反映为初始阶段随消散次数的增加而迅速减小,之后减小幅度减缓并有稳定的趋势.
可以看出,在笔者假设的前提下,第1次完全固结后,道路的沉降主要以排水固结产生的变形为主,循环荷载直接作用引起的瞬时塑性累积变形可忽略.由固结引起的土样的动变形与排水量的发展密切相关,表现为随固结次数的增加,最初较大,之后幅度减小并趋于稳定.

图10 固结排水量随固结次数变化Fig.10 Relationship between drainage volume and consolidation times
本文对饱和黏土在交通荷载作用下的工况做了简化,将不排水动力剪切与孔压消散阶段分开考虑,但现实生活中,很难将二者完全分开,且不同的排水条件下,孔压消散程度也不同,完全固结只在特定情况下才得以实现. 故今后有必要针对不同工况开展更多的工作.
3 结 论
(1) 循环荷载引起的动孔压完全消散后,黏土的刚度与动强度将有明显提高,在保持原动荷载水平不变情况下,瞬时轴向塑性变形基本不再变化.此性质对于本次试验中采用的粉质黏土、软塑黏土、可塑黏土均适用.
(2) 经历第1次孔压完全消散后,黏土的变形主要由固结时产生的轴向应变决定,其值相对初期瞬时轴向塑性变形较小.
(3) 随着固结次数的增加,相同动荷载水平作用下产生的动孔压不断减小,并有稳定的趋势;固结时的排水量亦有相同的变化规律.
(4) 固结度对于土样的动变形有较大影响.随着固结度的增加,变形不断减小.
[1] 叶耀东,朱合华,王如路. 软土地铁运营隧道病害现状及成因分析[J]. 地下空间与工程学报,2007,3(1):157-160,166. Ye Yaodong,Zhu Hehua,Wang Rulu. Analysis of the current status of metro operating tunnel damage in soft ground and its causes[J]. Chinese Journal of Underground Space and Engineering,2007,3(1):157-160,166(in Chinese).
[2] 日本道路协会. 道路土工软土地基处理技术指南[M].蔡思捷,译. 北京:人民交通出版社,1989. Japan Road Association. A Technical Guide to Ground Treatment in Road Engineering[M]. Cai Sijie,trans. Beijing:China Communications Press,1989(in Chinese).
[3] Miura N,Fujikawa K,Sakai A,et al. Field measurement of settlement in Saga Airport Highway subjected to traffic load[J]. Tsuchi-to-Kiso,1995,43/44/45/46 (449):49-51.
[4] Monismith C L,Ogawa N,Freeme C R. Permanent deformation characteristics of subgrade soils due to repeated loading[J]. Transport Research Record,1975,537:1-17.
[5] Chai J C,Miura N. Traffic-load-induced permanent deformation of road on soft subsoil[J]. Journal of Geotechnical and Geoenvironmental Engineering,2002,128(11):907-916.
[6] Hyodo M,Yasuhara K,Hirao K. Prediction of clay behaviour in undrained and partially drained cyclic tests[J]. Soils and Foundations,1992,32(4):117-127.
[7] 周 健,屠洪权,安原一哉. 动力荷载作用下软黏土的残余变形计算模式[J]. 岩土力学,1996,17(1):54-60. Zhou Jian,Tu Hongquan,Yaswhara K. A model forpredicting the cyclic behavior of soft clay[J]. Rock and Soil Mechanics,1996,17(1):54-60(in Chinese).
[8] 张 茹,涂扬举,费文平,等. 振动频率对饱和软黏土动力特性的影响[J]. 岩土力学,2006,27(5):699-704. Zhang Ru,Tu Yangju,Fei Wenping,et al. Effect of vibration frequency on dynamic properties of saturated cohesive soil [J]. Rock and Soil Mechanics,2006,27(5):699-704(in Chinese).
[9] 蔡 英,曹新文. 重复加载下路基填土的临界动应力和永久变形初探[J]. 西南交通大学学报,1996,31(1):1-5. Cai Ying,Cao Xinwen. Study of the critical dynamicstress and permanent strain of the subgrade-soil under the repeated load[J]. Journal of Southwest Jiaotong University,1996,31(1):1-5(in Chinese).
[10] 黄茂松,李 帅. 长期往复荷载作用下近海饱和软黏土强度和刚度的弱化特性[J]. 岩土工程学报,2010, 32(10):1491-1498. Huang Maosong,Li Shuai. Degradation of stiffness and strength of offshore saturated soft clay under long-term cyclic loading [J]. Chinese Journal of Geotechnical Engineering,2010,32(10):1491-1498(in Chinese).
[11] 李广信. 高等土力学[M]. 北京:清华大学出版社,2004. Li Guangxin. Advanced Soil Mechanics[M]. Beijing:Tsinghua University Press,2004(in Chinese).
[12] 雷华阳,姜 岩,陆培毅,等. 交通荷载作用下结构性软土动应力-动应变关系试验研究[J]. 岩石力学与工程学报,2008,27(增1):3052-3057. Lei Huayang,Jiang Yan,Lu Peiyi,et al. Experimental study on dynamic stress-strain relation of structural soft soil under traffic load [J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(Suppl 1):3052-3057(in Chinese).
Clay Dynamic Deformation with the
Consideration of Dissipation of Pore Pressure
Zheng Gang1,2,Huo Haifeng1,2,Lei Huayang1,2,Zhang Liming1,2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China;2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education,Tianjin University,Tianjin 300072,China)
During the research of dynamic response of saturated clay, undrained triaxial tests are usually conducted. Based on the fact that the saturated clay will ceaselessly drain overtime, tests were carried out to investigatethe undrained shear behavior of saturated clay after the dissipation of excess pore pressure. The results show that stiffness and dynamic strength will increase after consolidation, and the axial plastic deformation changes little under the former dynamic loading level. When the dissipation of pore pressure and undrained shear are repeated, the axial deformation mainly comes from consolidation, and the excess pore pressure and drainage volume will decrease with the increase of consolidation times, then come to a steady value. The undrained shear deformation will descrease with the increase of consolidation degree.
dynamic deformation;dynamic pore pressure;consolidation;undrained shear
TU443
A
0493-2137(2013)03-0191-06
2012-02-07;
2012-03-05.
国家自然科学基金资助项目(51078262);国家重点基础研究发展计划(973计划)资助项目(2010CB732106);天津大学自主创新基金资助项目(2010XJ-0101).
郑 刚(1967— ),男,博士,教授,博士生导师.
郑 刚,zhenggang1967@163.com.
图2 考虑孔压消散黏土的动变形
Fig.2 Dynamic deformation of clay with consideration of
dissipation of pore pressure

