Optimal Ratefor Constant-Fidelity Entanglement in Quantum Communication Networks

Youxun Cai,Xutao Yu,and Yang Cao

(State Key Laboratory of Millimeter Waves,Southeast University,Nanjing210096,China)

Abstract In this paper,we propose an entanglement scheme for long-distance,constant-fidelity communication in quantum networks.We dis⁃cuss the optimal rate of entanglement that allows for constant fidelity in both elementary and multihop links.We also discuss time complexity and propose the mathematical order of the rate capacity for an entanglement scheme.We propose a recursive entanglement scheme,a simultaneous entanglement scheme,and an adjacent entanglement scheme mathematically analyze these schemes.The rate capacity of the recursive and simultaneous entanglement schemes isΩ(1/en),but the adjacent entanglement scheme performs better,providing a rate ofΩ(1/n).

Keyw ords rate capacity;constant fidelity;entanglement scheme;ad hoc quantum networks

1 Introduction

Q uantum processing and communication networks combine the disciplines of quantum mechanics and classical information science.However,quantum networks are more secure and efficient than classical networks[1]-[3].Quantum commu⁃nication networks are based on quantum teleportation,which is essential for transmitting quantum states and establishing quantum channels between nodes at a distance[2].Quantum teleportation exploits one of the most intriguing properties of quantum mechanics:entanglement.In quantum entanglement,Einstein,Podolsky,Rosen(EPR)pairs are generated and then distributed via fibers or optical free-space links.This allows different nodes to transport a quantum state by transmitting classical bitsrather than quantumbits[2].

At present,photons are primarily used as the carrier in quantum entanglement generation.They are used over distanc⁃es of some hundreds of kilometers(e.g 250 km on fiber links and 144 km on free space)[3].However,the success of entan⁃glement decreases exponentially with distance because of ab⁃sorption lossand detector noisein thetransmission channel.

A solution toentanglement delay istoinsert quantumrepeat⁃ers between different nodes[5],[6].Quantum repeaters can store quantum states and use protocols to perform quantum op⁃erations.A repeater protocol definesa sequence of three opera⁃tions:entanglement generation on elementary links,entangle⁃ment swapping,and entanglement purification[7].The proto⁃col should bewell designed tomaximizesuccessat each link.

Entangled photons are used to express quantum states as EPR pairs.With the development of quantum networks,quan⁃tum optics has attracted more research interests recently.Fi⁃delity is one of the most important topics in this field and is de⁃fined as the probability that a decoded message has the same amount of information after coding and transmission as it did before coding and transmission.High fidelity is essential in long-distance communication to make messages reliable.In long-distance entanglement generation,fidelity can be affect⁃ed by memory decay,local measurement errors,entanglement swapping,or entanglement purification failure[7].The upper bound of the entanglement generation rate between nodes con⁃nected by quantumrepeatersisdetermined by thesefactors.

The quantum entanglement rate of each elementary link can be calculated and measured for specific quantum ad hoc net⁃works.In a multihop network,optimized quantum repeater pro⁃tocols increase the rate of quantum entanglement to reach the upper bound.

There are two main approaches to optimizing quantum re⁃peater protocols:developing a new quantum repeater structure(using quantum mechanics),and adapting classical network concepts to the quantum network.In[8],the former approach is taken.A Duan,Lukin,Cirac,Zoller(DLCZ)protocol gener⁃ates and connects entangled pairs of atomic ensembles over short distances.The protocol couples a single photon with col⁃lective atomic excitation modes.In[9],Qubus(hybrid)repeat⁃ers are described.These repeaters perform operations on both local qubits and continuous-variable states(qubus).In[6],EPR generation rate in ad hoc quantum networks is investigat⁃ed.Several heuristic algorithms are also introduced to ensure constant,maximum fidelity.These algorithms include Entan⁃glement Swapping Scheme Search,and Shortest Path Entangle⁃ment Flow.Novel quantum broadcasting schemes,such as ring,angular,and regional broadcasting,are defined in a quan⁃tumrepeater architecture and areextensionsof classical broad⁃casting concepts[6].Nevertheless,only recursive entangle⁃ment is applied in the quantum repeater protocols,and the en⁃tanglement rate when the number of nodes tends to infinity has not yet been determined.

In this paper,we focus on the rate capacity of entanglement that ensures constant fidelity when the number of nodes in a multihop link tends towards infinity.We use concepts from classical ad hoc networks to optimize the rate in a quantum re⁃peater with a typical structure[7].We propose three entangle⁃ment schemes for quantum repeater protocols.These schemes are recursive entanglement,simultaneous entanglement,and adjacent entanglement.Through mathematical analysis,we show that recursive entanglement and simultaneous entangle⁃ment provide a rate on the order of 1/en.However,adjacent en⁃tanglement provides a rate on the order of 1/n,which indicates better performance.

In section 2,we provide background on the entanglement rate capacity for an elementary link.In section 3,we describe the entanglement rate capacity model of EPR pairs for a multi⁃hop link.In section 4,we propose three entanglement schemes that ensure constant fidelity to establish multi-hop links are defined,the mathematical derivation of the rate capacity for each scheme ispresented,and their performancesareanalyzed.

2 Entanglement Rate Capacity Model for an Elementary link

For elementary link,the average timeτijto generate an EPR pair isgiven as thesum of thedetection time 1/fPgand commu⁃nication time dij/c:

where dijis the Euclidian distance between two consecutive nodes i and j;f is the operating frequency in the quantum re⁃peater;Pgis the probability of realizing an EPR pair;and c is the speed of light.For the quantum repeater in[7],Pgis

where F is the fidelity of the EPR pair between nodes,andηis the loss parameter,given by e-ξd,where d is the distance andξ is the rate of loss.The operating frequency depends on the quantummemory space M and link distance d[7]:

Therefore,the maximum operating frequency is[7]

Communication time is much shorter than detection time,i.e.(d/c)＜＜(1/(f Pg)).Therefore,the average EPR generation time is approximately equal to the detection time.A elementa⁃ry link's capacity for generating EPR pairs can be defined as the reciprocal of the maximum average time to generate an EPRpair,and isgiven by

3 Entanglement Rate Capacity Model for a Multihop Link

In practice,it is very difficult to transmit entangled photons over long distances because of channel loss and detector noise.It is reasonable to assume that entangled photons generated by a locate node can only be delivered to the consecutive node in a multihop link.A relay scheme is therefore used to ensure that any nodes over a long distance can share EPR pairs.Sup⁃pose Alice,Bob and Candy are three consecutive nodes in mul⁃tihop link.Alice can transmit entangled photons directly to Bob but not to Candy.First,photons are entangled so that Al⁃ice can share the them with Bob through elementary link(A,B).At the same time,Bob shares entangled photos with Candy through elementary link(B,C).As a result,Bob has a photon from the EPR pair with Alice.He also has a photon from the EPR pair with Candy.Second,we perform entanglement con⁃nection on the two photons that Bob has.This involves consec⁃utively swapping and purifying the entanglements.Third,we inform Alice and Candy about the classic information pro⁃duced by the quantum operation.Alice and Candy use this in⁃formation to operate the other entangled photons left in the quantum memory.Hence,by consuming two EPRpairs,we ob⁃tain an EPR pair between Alice and Candy,both of whom are unable to directly transmit photons.Using this relay scheme,more nodes can be added in multihop scenario,and fidelity can be constant for a remote node if entanglement swapping and purification arebalanced.

In the case of three nodes(Fig.1),we assume that entangle⁃ment occurs in the two elementary links at the same time.The average time for this process to occur has a lower bound of maxTheprobability of entanglement connection is determined by thephysical structureof the quan⁃tum repeater and is denoted Pc.The minimum average timeτACto obtain an EPR pair between Alice and Candy can be ex⁃pressed as:

▲Figure1.Entanglement for threenodes.

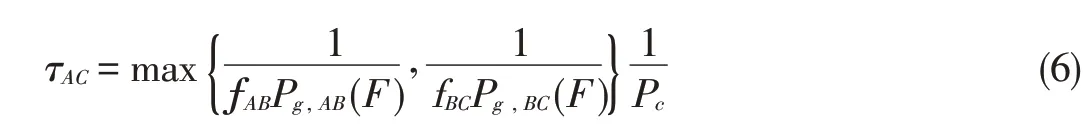
Moreover,the maximum average rate R(A,C)can be ex⁃pressed as

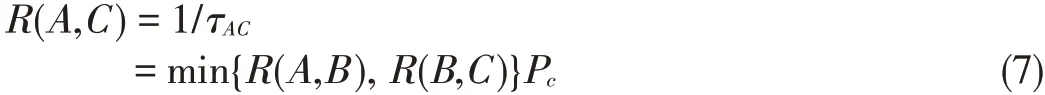
For n consecutive hops,entanglement connection can be doneon the k th repeater,and

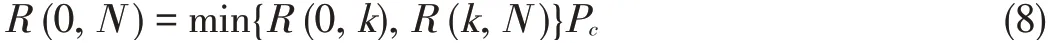
4 Three Entanglement Schemesfor Establishing Multihop Links

To create an EPRpair between the source node and destina⁃tion node,intermediatenodes are essential becausethey gener⁃ate EPR pairs and follow swapping steps to transmit an entan⁃glement.Take,for example,a finite multihop link with n nodes.If we know the exact entanglement rate between each pair of consecutive nodes,we can choose the appropriate se⁃quence scheme for entanglement on a node.In this way,the rate of entanglement can be optimized.In this paper,we are mainly concerned with the upper bound on the rate capacity with high probability(w.h.p);i.e.with probability tending to 1 as n approaches infinity.In the following,we use a probabilis⁃tic variation to denote the mathematical order.As n approach⁃es infinity,f(n)=Ω(g(n))w.h.p.as n approaches infinity.If thereisaconstant K,then

4.1 Recursive Entanglement Scheme

Recursive entanglement is an immediate scheme in which only one intermediate node is chosen for entanglement connec⁃tion at every turn.This process is repeated recursively so that an EPR can be established between the source node and desti⁃nation node in a multihop scenario.The start node can be se⁃lected arbitrarily,and entanglement connection should be doneat recursively before or after the node.

If the source node is chosen as the start node,the process for an n-1 hop path in the ad hoc quantum network is as in Fig.2.The arrows in Fig.2 indicate EPRpairs between nodes,and the triangles below the nodes indicate entanglement con⁃nections.Therecursiveschemeinvolves n-1 steps:

▲Figure2.Recursiveentanglement when thesourcenodeisthestart node.

1)Each node generates entanglements and shares an EPR pair with the adjacent nodes(Fig.1).Node 1 shares an EPR pair with node 2,and node 2 shares an EPR pair with node 3.Node n-1 sharesan EPRpair with node n.

2)Entanglement connection is done in node 2,and then node 2 sends the classical information to node 3 so that node 1 can sharean EPRpair with node3.

3)Entanglement connection is done in node 3,and then node 3 sends the classical information to node 4 so that node 1 can sharean EPRpair with node4.…n-1)Entanglement connection is done in node n-1,and then node n-1 sends the classical information to node n so that node 1 can share an EPRpair with node n.

The time taken to send classical information is negligible.Therefore,by applying(8)recursively,wecan concludethat

It is not necessary to choose node 1 as the starting node for the whole process if we know the exact entanglement genera⁃tion rateof each elementary link.Then,wecan useheuristic al⁃gorithms to determine which node to use as the start node and how to recursively doexecute theprocess.In thisway,themax⁃imumvalueof R(1,n)can beobtained.However,herewemain⁃ly focus on the mathematical order of R(1,n).Considering there are always n-1 steps,we let R(k th)be the rate of the ele⁃mentary link between the k th node and the next node at which entanglement isdone.Then,weconcludethat

where r isa constant,andɑ=1/Pc.The recursive entanglement schemeonly providesarateon theorder of 1/en.

4.2 Simultaneous Entanglement Scheme

Simultaneous entanglement was first described in[5].A quantum routing mechanism was proposed to construct the quantum communication network.Here,we describe the math⁃ematical order of the simultaneous entanglement swapping scheme(Fig.3).This scheme allows entanglement connection in parallel(rather than recursively)at the intermediate nodes.All the classical information is collected and applied to a spe⁃cially designed quantum logical circuit in the destination node.Then,the source and destination are entangled.This scheme involvesthreesteps:

▲Figure3.Simultaneousentanglement.

1)Each node generates entanglements and shares an EPR pair with the adjacent nodes(Fig.2).Node 1 shares an EPR pair with node 2,and node 2 shares an EPR pair with node 3.Node n-1 shares an EPRpair with node n.

2)Entanglement connection is done in parallel at all the inter⁃mediatenodes.

3)All the intermediate nodes send the classical information to node n.This information is received and processed at node n with a special quantum logical circuit.Node n then shares an EPR pair with node 1.

The time needed to send classical information is negligible,and all the n-2 entanglement connections should occur suc⁃cessfully at the same time.By applying(8)simultaneously,we concludethat

The simultaneous entanglement scheme only provides a rate on theorder of 1/en.

4.3 Adjacent Entanglement Scheme

In both the recursive and simultaneous entanglement schemes,the whole entanglement progress is a sequential chain of successful entanglement connections of each interme⁃diate node.Therefore for an n-1 hop link the total probability is always presented as a constant multiplied by an n-2 power of Pc.To decrease the mathematical order of the entanglement rate,we propose using the adjacent entanglement scheme.The main idea of adjacent entanglement is to divide the multihop link intosetsthat contain adjacent nodes.Thisensuresthat en⁃tanglement connection is done independent to that of other sets.After nodes in each set have performed entanglement con⁃nection,cluster sets are formed by small sets and continue with entanglement connection independently.Because entan⁃glement connection occurs independent of other sets,the total probability is multiplied by Pconly once at every turn,and the order decreases.We describe a concise scenario in which there are only 2knodes in a multihop link(Fig.4).

▲Figure4.Adjacent entanglement schemefor an a nodelink.

The adjacent entanglement scheme involves 2(log22k-1)steps:1)Each node generates entanglements and shares an EPR pair with adjacent nodes(Fig.4)Node 1 shares an EPR pair with node 2,and node 2 shares an EPR pair with node 3.Node n-1 sharesan EPRpair with node n.

2)The link is divided into 2k-2sets.Set 1 contains nodes 1 to 4,set 2 contains nodes 5 to 8 etc.Set i contains nodes 4i-3 to 4i,where i is an integer.Set 2k-2contains nodes 2k-3 to 2k.

3)Entanglement connection is done at nodes 2,3,6,7,...,4i-2,4i-1 at the same time.These connections are inde⁃pendent.By the end of step 3,node 1 isentangled with node 4,node 5 is entangled with node 8 etc.Node 4i-3 is entan⁃gled with node4i etc.

4)Entanglement connection is done at nodes 4 and 5 so that node 1 is entangled with node 8 etc.Entanglement connec⁃tion isdoneat nodes8i-4 and 8i-3 etc.

5)Entanglement connection is done at nodes 8 and 9 so that node 1 is entangled with node 16 etc.Entanglement connec⁃tion isdoneat nodes16i-8 and 16i-7 etc.

6)Entanglement connection is done at nodes 16 and 17 so that node 1 is entangled with node 32 etc.Entanglement connec⁃tion isdoneat node32i-16 and 32i-15 etc.…2(log22k-1).Entanglement connection is done at node 2k-1and 2k-1+1 sothat node1 isentangled with node2k.

The time needed to send classical information is negligible,and each set is independent.Each time entanglement connec⁃tion isdone,Pcis only multiplied once because of thisindepen⁃dence.Therefore,for a link with 2khops,the total probability isaconstant multiplied by a2(log22k-1)power of Pc.

In asimple8-nodescenario,

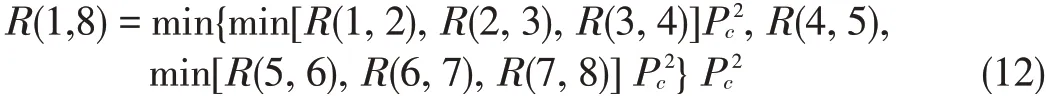
Therefore for an 8-hop link,the total probability is a con⁃stant multiplied by a 2(log28-1)power of successful connection probability Pc.For n→∞,the integer k=「log2n■makes n≤2k,and

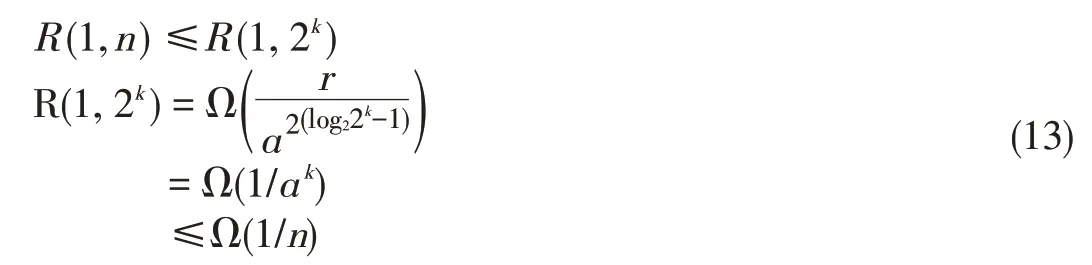
Therefore,the adjacent entanglement scheme can only pro⁃videarateon theorder of 1/n.

5 Conclusion

In this paper,we have discussed the optimal rate of entan⁃glement that can be achieved while still maintaining constant fidelity in a quantum communication network.Our discussion focused on a network in which the number of nodes in a multi⁃hop link approaches infinity.We proposed a recursive entan⁃glement scheme,a simultaneous entanglement scheme,and an adjacent entanglement scheme.These ensure constant fidelity when establishing multihop links.However,mathematical anal⁃ysis shows that the recursive and simultaneous entanglement schemesonly providearateon theorder of 1/enwhereasthead⁃jacent entanglement scheme performs better,providing a rate on the order of 1/n.