边坡动力可靠性分析方法的模式、问题与发展趋势
刘 晓,唐辉明,熊承仁
(1. 中国地质大学(武汉)教育部长江三峡库区地质灾害研究中心,武汉 430074;2. 科罗拉多矿业大学 土木与环境工程系,美国 科罗拉多州 戈尔登 80401)
1 引 言
边坡的稳定性问题是工程地质和岩土工程两大学科中的基本课题之一。人类对边坡稳定性的研究经历了两次飞跃:即从定性判断到定量分析的飞跃,从确定性理论到不确定性理论的飞跃。
1776年法国工程师库仑提出直线滑动理论,标志着边坡稳定性评价开始进入定量评价阶段[1]。20世纪50年代后,边坡稳定性评价理论逐步形成了以极限平衡理论(limit equilibrium method,LEM)居主导,有限元(finite element method,FEM)、有限差分(finite difference method,FDM)等数值方法为辅的定量评价理论体系[2-6]。基于确定性理论的这些方法,其缺点是没有考虑岩土体物理力学性质客观存在的不确定性,如材料参数(摩擦系数、黏聚力、重度等)的变异性和相关性,边界条件的不确定性(例如边界几何、初始应力场、孔隙水压力及外荷载的波动性等),以及理论模型的不确定性(所采用理论本身的近似性及其对不同边坡实例的敏感程度)等。
对不确定性问题的研究是现今科学界的重大研究方向之一[7]。自1967年Crawford等[8]首次将可靠度理论应用于土坡稳定性分析以来,学术界正在经历第2次飞跃,即逐渐接受不确定性的概念,在边坡稳定性评价和设计中引入可靠性分析方法。边坡可靠度分析方法是以获取稳定系数的各种确定性理论为基础,通过建立极限状态方程,以可靠度指标和失效概率作为稳定性评价标准。因此,基于不确定性理论的评价指标体系本身涵盖了确定性理论框架下的稳定系数,其来源于确定性理论,而又高于确定性理论,能更好地为工程决策提供依据。得益于计算机软硬件性能的爆发性增长,许多在20世纪80、90年代被认为虽然有前途,但过于复杂、计算效率不高、不经济的可靠度分析方法(例如Monte Carlo法),近年来获得了迅速的发展[9-15]。与之相应,边坡可靠性研究俨然已经成为岩土工程界的热点之一。许多国家和地区的学术机构已经或正在编制相关风险分析的规范。在美国,风险分析已经被大坝设计委员会接受;在香港、法国等地的边坡稳定分析和评价中,风险分析起着重要的决策作用。陈祖煜[16]指出:在滑坡和建筑物抗滑稳定分析中应逐步采用可靠度设计方法。
与结构工程发展的脉络相似,边坡可靠性研究将遵循从静力学领域向动力学领域的扩展和深化。静力学问题是动力学问题的特例,将边坡可靠性研究拓展到更具一般性的动力学领域是大势所趋,也是将研究不断推向深化的必然选择。特别是汶川大地震以来,全球范围内6级以上地震频发,地震进入高活跃期,这对边坡工程界提出了新的挑战。面对新兴领域,有需求就会有动力,大规模复杂岩土体可靠性问题的研究需求,必将极大地推动可靠度理论与各种非线性优化方法的结合研究,这对带动相关交叉学科的发展、催生新的学科生长点,具有重要的理论价值。
当前国际上对边坡动力可靠性分析方法的研究总体上正处于初始阶段。本文即是在这样的背景下,总结边坡动力可靠性分析方法的模式,分析存在的问题,对今后发展的方向提出预测。
2 静力可靠性分析法的模式分类
2.1 模式分类的必要性
现有的边坡动力可靠性评价理论和方法均是源自静力可靠性理论体系,因此,有必要对边坡静力可靠性研究的理论构架进行回顾与总结,并在此基础上对不同分析方法进行模式分类。
更重要的是,模式分类研究对于动力学领域还具有特殊的意义。与静力学问题不同,由于动力学问题的规模大,因而对算法的资源消耗(程序执行所需要耗费的时间、所占用的内存空间等)敏感,特别是在时间消耗上十分巨大。这就需要借助“计算复杂性理论”(computational complexity theory)的分析手段对不同的可靠性分析方法在数字计算机上实现的困难程度进行衡量,进而从算法的“可计算性”(computability)角度筛选出适用的动力可靠性分析方法。开展可靠性分析方法的模式分类即是实现上述目的的前提和基础。
以往涉及边坡可靠性分析方法的研究,大多专注于方法的本身,即致力于如何改进或者提出新的方法等,鲜见有关模式分类的相关研究。这主要是由于在静力条件下,各种算法的时间消耗和对内存空间的占用均在可承受的范围内,甚至某些以极限平衡法为基础的分析过程转瞬即可完成,因而是否开展计算复杂度分析显得并不十分迫切。与之相反,进入到动力领域,情况则大为不同:即便是简单模型的动力反应分析都涉及大量复杂的计算过程,计算效率问题愈发突出,已经成为必须解决的现实问题。因此,当研究的领域从静力问题拓展到动力问题后,开展不同可靠性分析方法的模式分类研究,进而评估不同模式的计算复杂度,已成为一种切实的需求。
2.2 边坡可靠性分析的理论构架
在边坡可靠性分析中,一般定义极限状态方程为
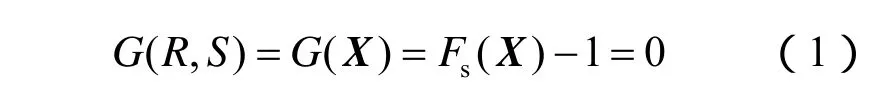
式中:G称为系统的功能函数;自变量R和S分别为结构的抗力和荷载效应,具体到边坡稳定性问题,R和S可以概化为向量X,包含影响边坡稳定性的各种参数(岩土力学参数、外部荷载等);Fs为稳定性系数。由上式稳定系数的引入,可以清楚地看到,系统功能函数实际上反映的是系统所储备的安全余量。当安全余量大于0时,系统处于稳定状态;当安全余量等于0时,系统处于极限状态;当安全余量小于0时,系统处于失效状态,进而有如下定义:

式中:Pf为失效概率;f(X)为功能函数G的联合概率密度分布函数。此外,还引入可靠度指标β,定义为功能函数的数学期望与标准差之比,即
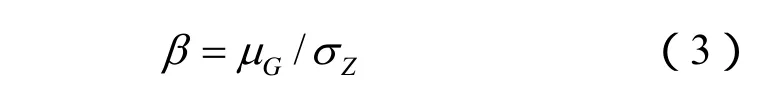
式中:μG和σZ分别为功能函数G的数学期望与标准差。
边坡可靠性分析方法是确定性的评价方法与可靠度理论相结合的产物。数学上,对不确定性问题最终都是转换为若干确定性问题进行处理,总的解决模式是:以确定性分析方法为内核,外部嵌套可靠性分析方法。对于式(1)中获取稳定系数 Fs的各种具体的实现方法,就属于确定性分析方法的范畴,是可靠性分析的内核;而求解式(2)与式(3)中失效概率 Pf与可靠度指标β的各种方法则属于外部嵌套的可靠性分析方法。
从数学建模的角度,内核所采用的确定性方法体现了研究对象的特有属性,依据研究领域和对象的不同而表现出很大的差别;而外部嵌套的可靠性分析方法一般具有通用性,其功能是对内核函数的响应进行数据处理,它将内核视为“黑箱”,不必深究其内部的物理含义,只需获得对应的输入与输出关系,即可实现可靠性分析。
2.3 边坡可靠性分析的6种模式
目前边坡可靠性研究中,所采用的确定性分析方法以传统的极限平衡法占据主导地位,近年来数值方法有上升的趋势[11-13,17-19]。前者以Bishop法、Morgenstern-Price法、Spencer法等为代表,后者以有限元法为代表。在可靠度分析方法方面,也可以归为两大类:一类是基于少量关键点采样的方法,主要有一次可靠度法(first-order reliability mehthod,FORM,含中心点法和验算点法等)、概率矩点估计法(point estimate method,PEM;Rosentlueth法)等;另一类是Monte Carlo及其衍生的随机模拟方法。鉴于后者在理论上可以无限逼近真实解,从而获得比第 1类方法更为精确的解答,因此,El-Ramly[20]将第 1类方法称为近似方法。笔者认为,从原理上将第1类方法称为“广义点估计法”较为合适,既能表达其基于小样本抽样理论的特色,又可以与已有狭义的概率矩点估计法相区别。图1(a)~(d)给出了两种力学分析内核以及两种外部嵌套的可靠性分析方法之间的两两组合模式。

图1 边坡静力可靠性分析方法的6种组合嵌套模式Fig.1 Six nested models of slope static reliability analysis methods
值得注意的是,响应面(response surface)理论的引入使得可靠性分析的内核有了新的演化。极限状态方程是描述边坡可靠性问题的数学基础,由于系统的复杂性,无论是采用极限平衡法还是以有限元为代表的数值方法,系统的极限状态方程始终处于高度非线性的隐式形式。响应面法的目标即是用某种显式的函数去拟合系统的极限状态方程,一旦确定了响应面函数,就可以用其直接计算待求采样点的函数值,也就是通过该函数来“代理”复杂的隐式内核,实现可靠度求解的简化。图 1(e)、(f)给出了以此为内核的两组合模式。相比其他两种内核(LEM与FEM),图1(e)与图1(f)模式不能直接通过内核获取边坡的稳定系数,需要先借助极限平衡法或数值方法来构建响应面,进而实现稳定系数的输出。在这两种可靠性分析模式中,响应面处于承上启下的地位,因此,又可以将响应面看作是一种中间层次。图2从数据流的视角给出了图1中6种模式的数据流层次示意图。
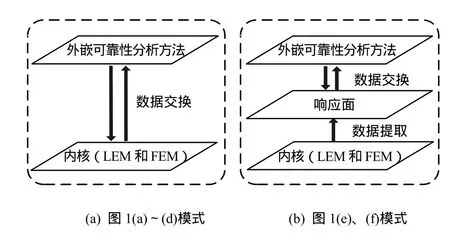
图2 6种组合嵌套模式的数据流层次Fig.2 Level charts of data flow for the six nested models
响应面函数虽然并不直接反映物理力学意义,但它提取自LEM或FEM内核,并可将其替代,其优势在于可以高效率地实现内核所具备的功能。
最初的响应面函数一般采用二次多项式拟合的方式[21],由于其函数形式较为简单,因此不仅效率高,而且使得外部嵌套的 JC法(广义点估计的一种)模块也有很好的收敛性,一度获得了迅速的发展,但其简单的函数形式同时也带来泛化性能欠佳的缺陷。由于寻找适合的响应面需兼顾其精度和效率,其本质上是个高度非线性函数的拟合和泛化问题,因此天然地与当前机器学习领域的进展密切相关,近年来发展很快,已经涌现出采用神经网络和支持向量机等新的响应面形式[18,22-23]来求解边坡可靠性问题。
2.4 6种模式的时间复杂度分析
计算复杂度分为时间复杂度(time complexity)和空间复杂度(space complexity),时间复杂度用以度量算法执行的时间长短,而空间复杂度则是衡量算法在执行中所需存储空间的大小,也就是对内存的消耗量。对边坡可靠性分析方法而言,制约其实际应用的主要是时间复杂度,上述6种模式之间存在数量级上的显著差别。各种组合模式算法的时间复杂度由其内核——边坡稳定性分析方法与嵌套在外的可靠性分析方法共同决定。
首先,分析计算内核的时间复杂度。精确比较极限平衡法与数值方法的计算时间消耗是比较困难的,不同分析案例之间的测试结果会因为所采用的具体方法和参数的不同而存在较大的离散性。实际上,计算复杂性分析所关注的是数量级上的差别,并不需要过于精确的比较。根据笔者的实际测试,若以执行1次极限平衡分析为1个基准单位考虑,则有限元类的数值方法,其时间复杂度大致为1000个单位左右。
其次,分析外嵌分析方法的时间复杂度。对于边坡可靠性问题,一般广义点估计法对内核调用的需求在几次至十几次之间,一般不超过100次。因此,从数量级的角度,以10次来评价广义点估计法是恰当的。至于蒙特卡洛法,由于循环次数与精度密切相关,不同的学者出于精度和效率的综合考虑,所选取的循环次数有较大的差别,但从现有的主流研究成果统计,其循环的数量级一般为1000。
再次,如图 1(e)、(f)所示,以响应面为内核的模式,其时间复杂度与前4种模式不同。图1(e)、(f)两模式的计算过程分为两个步骤:第一,建立响应面;第二,以外嵌可靠性分析方法驱动响应面,实现可靠性分析。由于极限状态方程已经显式化,无论是配合广义点估计法还是极限平衡法,一旦确立了响应面,则外部嵌套的方法所调用的是显式方程,与前4种隐式内核相比,具有很高的效率。拟合系统的极限状态方程需要的采样次数的数量级一般为10,若采用极限平衡法,则构建响应面的计算复杂度为10个单位,若采用数值方法,则相应的计算复杂度为10×103=104个单位。由于响应面函数的高效率,使得外嵌可靠性分析方法所消耗的时间大大减少,与构建响应面的时间消耗相比,不在同一数量级。根据计算复杂度理论,图1(a)~(d)模式的外层与内核对总体时间复杂度的贡献表现为相乘的关系;而对图 1(e)、(f)模式的两个步骤而言,其时间复杂度表现为相加的关系,考虑到数量级上的差别,图 1(e)、(f)模式中外层循环的时间消耗可忽略不计。
综上所述,图1对应给出了边坡静力可靠性分析方法6种组合模式的时间复杂度,以O表示。在已有的边坡可靠性研究文献中,大部分偏重方法的阐述,很少涉及到算法的复杂度分析,这主要是静力问题对计算复杂度研究的需求不高所致。而本文在此开展计算复杂度分析,主要是为后续定量评估动力可靠性分析方法奠定基础。
3 从静力可靠性到动力可靠性
3.1 边坡动力稳定性分析方法
与静力问题类似,边坡动力可靠性分析方法仍然遵循嵌套模式,确定性理论框架下的边坡动力稳定性分析方法是动力可靠性研究的内核和基础。为此,有必要对确定性理论框架下的边坡动力稳定性评价方法的研究进展进行简要概括。
地震和爆破震动作用下,人类对边坡稳定性评价的需求是边坡稳定性研究从静力学拓展到动力学的直接驱动力。其分析方法主要有拟静力法和数值法两大类。其中,拟静力法其实质还是静力法,最大的缺陷是无法体现动力反应。
在动力破坏模式方面,郑颖人等[24]认为,地震边坡的破坏由潜在破裂区上部拉破坏和下部剪切破坏共同组成(简称拉剪破坏)。赵安平等[25]则依据水下爆破试验结果提出了新的动力破坏模式:基岩与厚覆盖层边坡在地震力作用下因浅表层张拉而导致表层松散体流坍。但这种破坏模式还需要进行深入的研究和验证。一个明显的问题是,虽然爆破方式能模拟高频和大振幅,但由于爆破试验波有效持续时间太短(0.05 s),即便按模型相似比换算为原型条件下仍远不足0.3 s[25],这与地震波形动辄几十秒至几百秒的实际情况相差两个数量级。显然历时太短也就不利于反映边坡在整个地震历程中的共振效应,而共振效应对边坡动力稳定性的影响至关重要。相关模型试验[26]、数值模拟[27-28]和实例研究[29]也表明,动力破裂面发育深度与静力状态下的最危险滑面大体相当,而并非浅表层破坏。鉴于此,本文倾向于认同拉剪破坏模式。
在评价指标方面,也主要有两大类:①第1类是以Newmark[30]提出的基于永久变形的方法为代表,广义上该类方法还包括基于质点震动加速度、速率和位移的评价指标[31]。这类指标的一个突出特点是:针对不同的具体案例,判断系统失效与否的阈值差异很大,并无统一的标准。②第2类是以稳定系数为评价指标,体现了与静力学问题的一脉相承。由于动力条件下,稳定系数成为一个随时间变化的随机变量,因此,如何给出类似静力条件下的单值评判标准就成为一个问题。为此,张建海[32]、张伯艳[33]、薄景山[34]等提出以稳定系数时程中的最小值作为稳定性评价指标;吴兆营等[35]提出以平均安全系数作为评价指标;刘汉龙等[36]则是从概率分析和能量的角度出发,提出以最小平均稳定系数作为评价指标。相比较而言,以最小稳定系数作为评价指标显得过于保守,因为随机荷载下边坡的瞬间失稳并不一定导致边坡彻底破坏;而平均安全系数可能会高估边坡的动力稳定性;最小平均稳定系数虽然最为合理,但仍然是基于确定性理论框架,其评价结果缺乏风险层面的考量,这就引出了边坡动力可靠性。
3.2 边坡动力可靠性分析理论构架的特点
与静力问题相比,虽然边坡动力可靠性分析的极限状态方程仍然沿袭式(1),但有两个突出的特点:①动力荷载作为一种外部荷载,以随机变量的形式在向量X中予以反映,即动力的随机特性也会影响边坡的动力可靠性评价结果。若仅仅着眼于岩土参数的随机性来讨论边坡的动力可靠性是不够的,因为即使是同一个边坡,在不同的地震波形输入条件下仍然会表现出不同的可靠性。而在静力问题中,外部堆载、构造应力场等一般是不变的,并且由于重力加速度为常量,使得对重力场的考虑实际上转化为岩土体密度的函数加以处理。因此,在边坡静力可靠性分析中,对自变量X实际上往往只需要考虑岩土体的物理力学性质即可。②静力稳定系数升格为动力稳定系数。在静力条件下,式(1)中稳定系数 Fs是随自变量X变化的一个单一变量。而在动力条件下,对每一个任意确定的系统输入X,稳定系数都升格为一个随机过程 Fs(t)。这就使得需要定义某种动力稳定系数,使之在整个动力反应时间域内具备综合评价能力。
3.3 边坡动力可靠性分析方法
如前所述,边坡动力可靠性分析中,对不确定性的考虑实际上包含岩土参数和动力荷载两大类,据此可将当前边坡动力可靠性分析方法划分为3种类型。
3.3.1 仅考虑岩土参数的不确定性
拟静力法(或称为等效荷载法),是一种用静力学方法近似解决动力学问题的简易方法,其基本思想是在静力计算的基础上,将动力作用简化为一个惯性力系附加在研究对象上,该方法实际上只考虑岩土参数的不确定性。在此指导思想下,图1中静力可靠性分析方法的6种组合嵌套模式都可以自由地迁移到动力领域,并且不会造成计算复杂度的增加,其原因在于拟静力法的实质仍然是静力法。
由于与静力可靠性分析方法天然的兼容性,目前,基于拟静力法的边坡动力可靠性分析方法处于主流地位,2000-2012年SCI-E收录的关于边坡动力可靠性评价方法的文献无一例外全部是基于拟静力法,见表1。

表1 2000-2012年SCI-E收录的边坡动力可靠性评价方法的4篇文献的模式分类与计算复杂度Table 1 Pattern classification and computational complexity of the 4 SCI-E citations which focused on slope dynamic reliability methods and were published during 2000 to 2012
3.3.2 仅考虑边坡动力反应
由于极限平衡法对刻画边坡的动力反应存在理论上的障碍,所以应采用有限元为代表的数值方法来分析其动力反应。对于动力学问题,即便是在确定性的岩土力学参数条件下,稳定系数也表现为一个随机过程。因此,研究动力问题自然地需要借助概率论的相关方法。
目前,包括边坡稳定性问题在内,考虑可靠度的动力稳定评价方法,都或多或少吸收了 Rice[39]和Coleman[40]的“超越概率”思想,即以边坡的随机动力响应过程δ(t)在规定的时间内,不超过限值δ= a 的概率来定义结构的动力可靠度,而失效概率的定义则恰好与之相反。具体的动力响应过程δ(t)可以取为稳定系数,也可以是质点震动加速度等类似的指标。杨仕教等[41]采用动力有限元方法,以爆破震动速率为评价指标,以国标 GB6722-2003规范[42]规定的允许震动速率的最大值为限值,分析了云南某铅锌矿高陡边坡的动力可靠性。刘红帅等[43-44]采用动力有限元方法,分析稳定系数时程曲线的概率分布特性,并汲取超越概率的思想,提出了在指定失效概率水平下,通过反算限值 Fr= a 来作为动力稳定系数。
总的来说,上述动力可靠性评价方法的实质是对某种物理量(如稳定系数、位移等)的动力响应随机过程进行概率分析,进而提取相关统计量的特征值。很显然,在不同的地震波形输入条件下,同一边坡表现出不同的动力可靠性,而上述方法实际上只考虑了某种特定动力波形,也就是说,将边坡的动力可靠性分析结果仅仅视为对某种特定动力荷载过程的响应,并且在此过程中并未涉及到岩土力学指标不确定性的影响,从这个意义上来说,这种动力可靠性评价方法对式(1)中自变量 X的考虑是不完备的,因此,就有了下面将要阐述的第3类边坡动力可靠性分析方法。
3.3.3 同时考虑岩土参数的随机性和边坡动力反应
考察图1所示的6种模式,都具备考虑岩土力学参数随机性的能力,但其中能克服拟静力法的固有缺陷、实现动力反应分析的是图 1(c)~(f)4种模式(其中图 1(e)、(f)两种模式的响应面应采用数值方法构建)。
如3.2节所述,在动力条件下,对每一个任意确定的系统输入X,稳定系数都升格为一个随机过程 Fs(t)。这就使得需要采取“降维”的方法消去时间尺度,通过定义某种动力稳定系数,使之在整个动力反应时间域内具备某种综合评价能力。刘汉龙等[36]提出的最小平均稳定系数,以及刘红帅等[43-44]提出的在某种指定失效概率水平下的动力稳定系数能够符合上述综合评价的需求。
必须指出的是,这种综合评价是对时间尺度的综合,也就是说,其目的是将随机过程降维,使之能套用式(1)。至于影响边坡稳定性的各种参数的不确定性影响,则是通过图1(c)~(f) 4种模式之一的求解来实现。
至此,这种动力可靠性评价方法最终具备了如下两个重要特性:①体现了边坡岩土体的动力反应;②考虑了岩土体物理力学性质的不确定性。目前,采用此方法的研究成果还十分缺乏,唐辉明等[45]采用此方法对汶川地震区边坡的动力可靠性进行了评价,效果良好。
4 2000-2012年SCI-E文献统计
笔者统计了2000-2012年SCI-E收录的致力于边坡和滑坡可靠性分析方法研究的46篇主要文献,涉及的主要研究内容分布如表2所示,其合计情况见表3,多角度分类饼图见图3,具有如下几个特点:
(1)如图 3(a),静力领域仍然是研究者最为关注的,而动力问题研究程度较低,仅有 4篇文献[15,22,37-38],只占8.70%,并且这4篇文献全部基于拟静力法,见表1。
(2)如图3(b),极限平衡法以其易用性强的特点,仍然居于主导地位,数值方法只占20.83%。
(3)如图3(c),按图1所列的6种嵌套模式分类,涉及模式图1(a)和图 1(b)的成果在数量上超过一半,这主要是由限平衡法居主导地位造成的。

表2 2000-2012期间SCI-E收录的46篇有关边坡和滑坡可靠性评价方法的文献主要研究内容分布Table 2 Distribution of main research contents of the 46 SCI-E citations which focused on slope &landslide reliability analysis methods and were published during 2000 to 2012

表3 表2中46篇文献主要研究内容合计Table 3 Summation table of main research contents of the 46 citations in Table 2
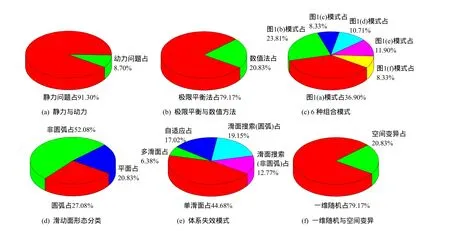
图3 表2中46篇文献研究领域的多角度分类饼图Fig.3 Pie charts on multiple-perspective classification of research fields based on the 46 citations in Table 2
(4)如图 3(d),在滑动面形态分类上,表面上看,非圆弧成果的数量大幅超过了圆弧滑动。这主要是借助强度折减法自适应定位滑动面的缘故(强度折减法具有刻画非圆弧滑动的能力),并不能说明涉及非圆弧滑动面搜索的技术方法已趋成熟并获得大量应用。25篇非圆弧成果中,11篇是指定滑动面,8 篇[11-12,17-19,21,62,68]借助强度折减法自适应定位滑动面,而仅有6篇[9,53,60,63,65,69]涉及非圆弧滑动面搜索。实际上,涉及非圆弧滑动面搜索技术的难点在于滑动面形态的数学描述和搜索结果的全局优化,这一直是土质边坡稳定性分析的重要问题之一[77-83]。
(5)如图 3(e),在体系失效模式方面,考虑有限个潜在滑动面(单滑动面和多滑动面)的情况占了一半,另有19.15%的成果借助强度折减法来回避滑动面的搜索问题,只有12.77%的成果涉及了难度最大的非圆弧滑动面搜索。
(6)如图 3(f),考虑岩土性质空间变异性的研究成果明显偏少。
此外,从时间的尺度分析,2011-2012年关于边坡可靠性评价方法的研究明显升温,涉及的文献数比2006-2010年的总和还要多。46篇文献的年度分布柱状图见图4。

图4 表2中46篇文献年度分布柱状图Fig.4 Annual distribution histogram of the 46 citations in Table 2
5 存在的问题
与静力可靠度分析方法的研究水平相比,现有的动力可靠度分析方法的研究水平明显偏低,突出表现在以下3个方面。
5.1 对不确定性考虑不足
如3.3节所述,现有的动力可靠性评价方法大多局限于两大类:①忽略动力反应,采取拟静力法使问题高度简化为静力求解;②对某种物理量的动力响应随机过程(例如,稳定系数时程)进行概率分析,进而提取某种特征统计量。前者的缺陷是显而易见的,而后者最为明显的缺陷是对不确定性的考虑很不充分。
首先,并未考虑岩土物理力学性质指标的不确定性,并且这种不确定性应当包含模糊性和随机性两种成分。考虑岩土参数的不确定性几乎是可靠性分析的标志性需求,因此,在动力可靠性分析中仍然沿用确定性的力学参数无疑是不完整的。
其次,并未考虑整个动力过程中最危险滑动面空间位置的变化,这实际上涉及体系可靠度的问题,在5.2节中将详细阐述。
再次,对失效状态的划分也并未引入模糊理论,而是采取一刀切的模式(稳定系数小于1,即判为失效),因而也不甚合理。
对不确定性的考虑是可靠性研究的灵魂,在特征物理量响应的不确定性、岩土力学性质的不确定性、最危险滑动面的不确定性、失效状态的不确定性这4个方面,当前的动力可靠性研究还仅仅停留在第1个方面,能同时涵盖全部4个方面的研究尚属空白。
5.2 体系可靠度求解方法的争论对动力领域的影响
在边坡可靠度分析中,对存在多个滑动面的情况,应作为一个体系来考虑[55,84-89]。对于岩质边坡来说,受控于大的结构面,一般认为潜在滑动面的数量是有限的,但对土质边坡来说,潜在的滑动面可以是无限多个,从系统可靠性的观点,土质边坡系统可以概化为无限多个滑动面组成的串联体系,任意一条滑动面失稳都将会造成系统的整体失稳。
实际上,边坡体系的可靠度问题无论是在静力还是动力领域都是前沿问题。而且,由于动力问题中瞬时最危险滑动面的空间分布位置存在很大的跳跃性,表现为一个随机过程,这使得体系可靠度问题在动力领域表现得更为突出。
总的来说,当前针对边坡体系可靠度问题有 4种处理方法,各种方法之间并不等效。至于何种方法更适用于边坡系统,则存在争议。
第 1种方法,为了简便起见,以某个滑动面上的可靠性指标作为系统的评估值。众多学者[1,20,90-93]提出了与最小可靠度指标对应的“概率临界滑动面”(critical probabilistic surface)的概念,并以此滑动面的可靠度近似作为体系的可靠度。其中 Hassan等[92]提出的搜索概率临界滑动面的一种简单方法,受到了广泛的关注,但因缺乏理论依据而受到质疑[94-96]。吴振君等[97]采用Low 等[98]提出的FORM优化解法,并结合广义简约梯度法与Hassan等[92]的简化方法做了对比。
第2种方法,是以岩土均值变量所对应的“最危险滑动面”(critical slide surface,也称为临界滑动面)为对象进行可靠性计算。谢桂华等[99]以费伦纽斯圆弧滑动为力学模型,采用遗传算法搜索了均值指标对应的最危险滑动面,并给出了其可靠度指标和失效概率。吴振君等[97]指出,该方法实际隐含了“边坡体系的失效概率等于边坡在此确定性滑动面上的失效概率”这一假定。祝玉学[100]认为,这种近似在大多数情况下是满足工程精度要求的。但在动力条件下,情况则明显不同,根据刘晓等[28-29]的研究,最危险滑动面的位置随着动应力场的变化表现出很大的差异性。而该方法所指的最危险滑动面是固定的、静态的,若应用于动力问题,其理论依据不足。
此外,学术界存在一种观点,对于上述“最危险滑动面”可以采用强度折减法进行“自适应”(或称为“自动”)定位,从而回避复杂的滑动面搜索作业[11-12],但根据刘晓[28]的研究,这种自动定位的滑动面与滑动面搜索结果并不总是保持一致,而是略有差别。这主要是由于强度折减前后应力路径的不同,造成边坡应力场的重分布,从而表现出应力场的轻微变化。如果说一般静力分析中,应用强度折减法定位最危险滑动面还并不需要特别关注这种应力场的变化,而一旦进入到动力领域,这恰恰是动力研究所需要密切关注的,因为动应力场在整个反应时程内往往表现出波澜壮阔的改变。所以强度折减法并不能替代各种滑动面搜索方法,其动力问题的适用性还需要进行更为深入的理论和实践探索。
第3种方法,对每次随机抽样的参数组合,搜索稳定系数最小的滑动面,分别得到一个确定性的临界滑动面及其对应的最小稳定系数,N次模拟后便可计算体系破坏概率和可靠指标[97],显然,这种方法借鉴于Monte Carlo方法的思想,其理论依据是大数定理。
第4种方法,是一个窄区间来锁定系统的可靠度的变化范围。由于各滑动面失效模式之间并不是彼此独立的,而是存在相关性,李典庆等[87]指出,若不考虑边坡各失效模式之间的相关性,会明显低估边坡体系的可靠度。但这种相关性很难直接定量描述,为此Moses等[101]、Cornell[102]提出的区间法,给出系统可靠度指标的上下限。Ditlevsen[103]将区间法进一步改进,缩减了区间的范围。理论上可以证明系统失效概率的下限不低于组成系统的各“元件”的最高失效概率,只有在各“元件”的相关性大到呈现出“包含关系”的极端情况下,才取等号(此时系统退化为“单一元件”系统),上述规律在很多学者给出的实例研究中[56,86,104-105]都得到了体现。区间法大多应用于评估有限个失效模式,但对于土质边坡这样的无限串联系统,区间法的实现则存在数学上的困难。
对于方法4,有严密的数学推导作为理论基石,其发展的方向首先是如何使得评估的区间尽量的压缩,提高精确度。而前3种方法的正确性,学术界一直存在争论[97]。Chowdhury 等[106]、Hassan 等[92]、陈祖煜[1]都曾指出,方法1和方法2得到的滑动面并不总是一致,并且Hassan等[92]认为,方法3因为得到的结果不是针对某条特定的滑动面,因而没有物理意义。实际上,这恰恰是其优势所在:方法 3的特点是着眼于串联体系的全局,不受“边坡体系的破坏概率必须对应某一滑动面”这一潜在思维惯性的影响,所得的评价指标并不拘泥于某一特定滑动面,因而更具有全局的观念。早在 1971年Cornell[102]就将串联体系的规律概括为:存在多个失效模式的体系,其总的失效概率大于其中任意一个失效模式的失效概率。通俗的说就是:串联系统可以比构成它的“元件”拥有更高的失效概率。因此,持“概率滑动面”观点的方法 1,显然是在搜索失效概率最大的“元件”,进而将这个元件的失效概率默认为系统的失效概率;而方法2则是以某一固定“元件”的失效概率作为系统的失效概率。显然,这两种方法都存在低估系统失效概率的可能。
与致力于相关性的解析思路(方法 4)不同,李典庆等[87]采用一种效率高于Mote Carlo法的自适应重要抽样(adaptive importance sampling,AIS)抽样方法来求解边坡体系可靠度问题,并且指出:随机抽样这类方法的优势是其本身不受失效模式之间相关或独立条件的限制,表面上看没有考虑模式之间的相关性,但实际上在计算过程中自然满足了功能函数间的相关性。持类似观点的还有El-Ramly等[20]和Altarejos-Garcia等[46],他们依据Monte Carlo法的普适性和高精度,将其作为检测和标定其他方法的准绳。因此,笔者认为,以Monte Carlo法的为依据的“方法3”理论上比其他3种方法更合理。而且,Monte Carlo方法的普遍适用性也决定了当系统由从有限的串联体系过渡到无限串联体系,也无论是静力问题还是动力问题,都可以获得求解。
关于方法3,其研究的空白点表现在两个方面:首先缺乏理论上强有力的证明。虽然其合理性可以从有关学者的成果[87,97,99]中窥见一斑,但总体上缺乏完整的证明。其次在于技术实现上的瓶颈,搜索稳定系数最小的滑动面,特别是有限元等数值方法下的非圆弧滑动面搜索问题,从来就不是一个简单的问题。即便是确定性领域的最危险滑动面搜索这个问题本身而言,已经是边坡研究的前沿之一。如果在可靠度分析中考虑“动”滑动面,将毫无疑问的嵌套这一具有相当难度的前沿问题。现有的可靠度研究大多是建立在对“定”滑动面的岩土力学参数随机分析上的,即使涉及滑动面搜索,也大多是在极限平衡框架下执行圆弧滑动面搜索算法。目前在数值方法理论框架下的,考虑非圆弧滑动面搜索的边坡可靠度研究成果[45]还十分少见。当问题上升到动力可靠性领域,则意味着在整个动力反应时程之中,要针对大量的瞬时应力场执行平行的搜索作业,实现起来更加困难。
边坡体系可靠度求解方法的争论对动力领域的影响比静力领域要显著得多。如果说静力问题中,不同的体系求解方法之间所关注的滑动面(概率临界滑动面和最危险滑动面)的空间分布位置在大部分案例下具有趋同性,但并不能总是保持一致,那么在动力时程的任意瞬间,这两者的差别是显著的、不断变化的、并贯穿于整个动力反应时程。这种显著的差异源于不断变化的动应力场的瞬时应力分布规律与常规重力场有很大的不同。
5.3 计算效能不足
当前,制约边坡动力可靠性研究向前发展的一个重要问题是计算效能的不足。动力问题与生俱来的复杂性,对硬件的计算能力提出了近乎苛刻的要求。当前,即便是确定性理论下的边坡动力稳定问题,其计算的时间开销已经很大,而动力可靠性分析需要循环嵌套这种确定性的动力分析,因而时间复杂度呈指数增长,计算效率成为关键问题之一。
根据实例研究[28-29],在当前主流PC工作站环境下,针对二维边坡进行基于数值方法的动力反应分析,其耗时以小时计;与之相比,执行静力数值分析的耗时以分钟计,效率相差超过10倍。据此估算,如果将图1(c)~(f)4种模式应用于动力分析,则计算复杂度和时间消耗估值见表4。

表4 固定滑动面条件下动力可靠性分析的时间复杂度Table 4 Time complexity of dynamic reliability analysis in the condition of fixed sliding surface
如前所述,鉴于极限平衡法对研究动力问题的局限性,表 4中并未列出图 1(a)~(b)两种模式。在图1(c)~(f)4种模式中,最为精确的当属图1(d)模式。这可以归为内、外两个方面的原因:该模式以数值方法为内核,对描述确定性框架下的动力学问题已经不存在理论上的困难;而且,正如El-Ramly等[20]所倡导的,Monte Carlo法本身的精确性能够很好地满足可靠性分析的要求。而图1(c)、(e)模式所采用的广义点估计法除了因为引入简化假设使得计算精度较差外,更面临可能计算不收敛的障碍,例如在极限状态函数比较复杂的情况下,JC法容易陷入不收敛。
在边坡静力可靠性领域,Griffith等[68]提出的方法可视为图1(d)模式的代表,受到了广泛的关注,Wu[107]认为,其代表了一类典型的分析方法。但遗憾的是,近年来并未见有与图1(d)模式相关的动力可靠性研究成果问世。笔者认为,制约该模式向动力学领域拓展的主要原因并不是理论上的障碍,而是计算效能的不足。在保守估计下,表4中列出的分析时间已经超过100 d(2400 h),超出了常规岩土仿真分析所能承受的极限。必须指出,表4中所列举的还仅仅是固定滑动面条件下的复杂度,如果考虑体系可靠度问题,则还需要在算法中嵌套进行滑动面的动态搜索,这无疑将大大增加计算的复杂度。因此,进行动力可靠性研究必须高度重视算法的效率,计算效能的瓶颈将使得理论可行的方法在实际运用中失去意义。
6 边坡动力可靠性研究的发展趋势
以目前的研究水平,边坡动力可靠性研究发展趋势可以归纳为以下3个方面。
6.1 对不确定性的考虑趋向全面和深入
当前,动力可靠性研究还未涉及岩土力学性质和边坡失效状态的不确定性,而在静力问题中这两个领域已有相关成果。鉴于随机性和模糊性是不确定性的两种最主要的表现形式。因此,动力可靠性研究的趋势之一是在岩土体物理力学性质的描述上继续深化随机理论,除了以常规的一维随机变量进行描述外,运用随机场理论来刻画空间变异性的研究[108]将逐步受到重视。例如,对二维边坡,岩土力学性质的空间变异性需要用二维随机变量来描述。目前考虑空间变异性的研究成果总体上较少,并且其中大部分局限于采用极限平衡法。而实际上,由于理论构架限制,极限平衡法仅仅只能反映滑动面上的岩土力学参数的空间变异性,而对其在整个边坡内的空间变异性则视而不见。相反,以有限元为代表的数值方法则不存在上述问题。目前采用数值方法开展考虑空间变异性的边坡可靠性研究的代表性文献见于Wang[76]、Griffiths[12,68]、Huang[11]等,总的来说,还比较少见,究其原因除了算法比较复杂、没有通用的商业程序可供借鉴和推广以外,实际应用中野外样本采集数量过少、往往达不到刻画空间变异性的最低要求,也是制约其应用一个重要的原因。随着研究的不断深入和边坡可靠性评估对精细化要求的提高,未来在此方面的研究必然会受到应有的重视。
趋势之二是将模糊性与随机性整合。这种整合表现在两个方面,即考虑岩土物理力学性质随机场的模糊性和边坡失效(破坏)状态判识的模糊性。对于边坡来说,模糊性是具有更深刻、更普遍意义的不确定性。模糊数学在表达人类的经验、定性描述等模糊的概念方面比经典的随机理论有较强的优势。例如,在对边坡失效状态的判别上,采用模糊判别显然比依据稳定系数“一刀切”地将边坡状态划分为“稳定”、“极限平衡”和“破坏”3种类型要合理得多,但遗憾的是,近13年来的SCI收录的边坡可靠性文献没有一篇涉足此领域(见表 2)。实际上,在同时考虑边坡岩土体力学性质的模糊随机性和极限状态的模糊性方面,贾厚华等[109]较早地给出了实现方法,但该文献还未来得及进一步考虑随机场的模糊性。可以预见,未来的边坡动力可靠度研究也将借鉴静力可靠度的发展脉络,朝着精细化的方向发展,逐步实现模糊性与随机性的深入整合。
6.2 对体系可靠度的研究趋向重视
边坡的体系可靠度问题由来已久,它实质上涉及最危险滑动面的空间定位问题,如果说在静力条件下还可以用近似的方法,以岩土性质处于均值条件下所对应的最危险滑动面作为系统固定的破坏面,以利于简化处理,则在动力条件下,最危险滑动面天然地具有显著的空间离散性,使得动力可靠性问题若沿用上述近似解法,必然存在相当大的误差,并且如5.2节所述,这种误差的指向性是导致低估系统的失效概率,偏于危险。因此,必须着力解决体系可靠度的理论和实践问题,研究的趋势分为理论和实践两个方面。
在理论研究方面,学术界在“搜索什么样的滑动面?是动态最危险滑动面还是概率滑动面”这个问题上存在争论。尽管当前的研究表明“方法 3”最趋合理,但解决争论的关键在于从理论上进行强有力的证明。这是今后边坡体系可靠度理论研究的趋势之一。
在具体实践方面,如何定位最危险滑动面?这无论是对确定性问题还是不确定性问题,也无论是对静力问题还是动力问题,都是无法回避的基本问题。在静力分析领域,上述问题亦是边坡研究的前沿方向之一,目前的趋势可以概括为3个“过渡”:由简单的圆弧滑动向非圆弧滑动过渡、由传统的基于极限平衡理论向基于数值方法的应力场理论过渡、由传统的非线性优化方法向新兴的群体智能优化方法过渡。第1种过渡反映了对滑动面几何形态刻画精度的需求正在提高,从圆弧滑动到非圆弧滑动,是一种跨越。非圆弧滑动其本身可退化为圆弧滑动的模式,因而更具有一般性。第2种过渡则反映了边坡稳定性分析的内核正趋向复杂化,特别是当问题延伸到动力分析领域,采用数值方法已成为一种必要。遗憾的是,表1中收录的4篇有关动力可靠度的文献[15,22,37-38]全部基于拟静力法(以极限平衡法为内核),不具备真正意义上的动力反应分析能力。第3种过渡则主要体现在滑动面搜索技术的进步。基于应力场的滑动面搜索流程可以描述为通过数值计算引擎(有限元或有限差分等)获取应力的时间-空间场,然后依据滑动面应力和抗滑力的积分算法来评估任意滑动面的稳定系数,而滑动面搜索技术即是要采取某种优化方法寻找稳定系数最低的滑动面。目前所应用的优化方法已经逐步从梯度法、牛顿法等常规方法[1]向群体智能方法[18-28,29,78-83]过渡。
6.3 提高计算效率
考察图1(c)~(f)4种模式应用于动力领域,由于广义点估计法在精度和收敛方面的缺陷,因此,应考虑从图 1(d)和图 1(f)两种模式中优选,也就是需要重点研究外部嵌套方法为Monte Carol的模式。
经典Monte Carol方法是可靠性分析的有力武器,但用于随机有限元(或有限差分等)这样一类数值分析领域,即图1(d)模式,则面临巨大的效率瓶颈:不仅在于因计算耗时大而显得很不经济,而且在于因耗时超过所能承受的限度而使得很多有价值的分析工作虽然在理论上不存在困难,但几乎无法应用于复杂案例的实践。尤其是动力分析领域,由于所采用的数值分析方法的高度非线性和离散性,再加之考虑模型参数的模糊和状态的模糊,极限状态曲面呈现出隐式、高维度的特点,巨大的计算量导致Monte Carol随机有限元模拟的效率问题尤为突出。
解决Monte Cralo模拟的效率瓶颈,可以从两个方向寻求解决的办法:提升硬件性能,或者改进算法。显然短期内提升硬件性能是不现实的,根据摩尔定律,计算机的运算速度不可能在短期内获得数百倍的性能提升,而且只靠提升硬件,实质上是回避问题,而不是解决问题,无法从本质上改变算法低效的现状。因此,根本出路在于找到更高效的算法。
构建新算法的关键在于,必须降低可靠度分析方法对采样点规模的依赖,否则问题的求解将会因为耗时过长而成为空谈。考虑到极限状态曲面实际隐含在求解的步骤之中,若能仅以少量采样点为代价,将隐式极限状态曲面近似的拟合,得到极限状态方程的显示表达,并作为Monte Carlo模拟的内核,从而构建新的快速随机模拟方法,则效率问题将得以解决。这就是图 1(f)模式的核心思想。该模式的时间复杂度主要由响应面拟合的时间消耗决定,一旦确定了响应面,则Monte Carlo模拟本身驱动响应面所消耗的时间与之不在一个数量级,可忽略不计。依据表4,图1(f)模式的时间复杂度比图1(d)模式要低两个数量级,效率提升十分可观。
寻找一种满足精度要求的、高效率的响应面代理方法是改进传统的Monte Carlo随机模拟方法的关键所在。这个问题实质上属于多维空间中极限状态曲面的拟合和泛化的研究范畴,其目标是在有限的训练样本条件下,获得高性能的响应面(精度高、泛化速度快)。从已有的相关研究成果来看,已有使用神经网络或支持向量机拟合极限状态曲面的报道[22-23,45],特别是学术界公认支持向量机有比神经网络更优异的泛化能力,而且计算速度快,这对动力学问题的大规模特点来说,正适得其所。可以预见,作为高效率的技术手段,未来以这些优秀非线性方法将会越来越多地应用于边坡动力可靠性分析的实践。
7 结 论
(1)静力学问题是动力学问题的特例,边坡可靠性研究从静力学领域逐步拓展到更具一般性的动力学领域是大势所趋,这也是研究不断深化的必然结果。现有的边坡动力可靠性评价理论和方法均是从静力可靠性理论体系发展而来。边坡静力可靠性分析方法可划分为6种组合嵌套模式,其中4种可拓展到动力反应问题,各种模式的算法时间复杂度在数量级上存在显著的差别。
(2)当前,边坡动力可靠性评价方法研究总体上正处于起步阶段,突出的问题表现在3个方面:①对不确定性的考虑还不够全面。在特征物理量响应的不确定性、岩土力学性质的不确定性、最危险滑动面的不确定性、失效状态的不确定性这4个方面,当前的研究仅仅停留在第1个方面,能同时涵盖全部4个方面的研究尚属空白。②边坡体系可靠度求解方法的争论对动力领域的影响显著。③动力问题对计算效能的需求大大高于静力问题,计算效率问题成为制约动力可靠性研究的技术瓶颈。
(3)未来边坡动力可靠性评价方法的发展趋势归纳为3个方面:①对不确定性的考虑将趋向深入。在岩土体物理力学性质的描述上,运用随机场理论来刻画空间变异性的研究将逐步受到重视。而且模糊性与随机性将期待获得深入的整合。②针对边坡体系可靠度求解方法存在争论的问题,今后从理论上进行强有力的论证是解决争论的关键。在体系可靠度的求解的具体实践上,将朝着分析方法精细化、考虑的不确定性因素复杂化的方向发展,将会更为广泛地与新兴的群体智能优化算法相结合,分析结果将更趋于合理。③高性能计算在动力可靠性分析中具有重要地位,在解决动力可靠性研究的计算效率问题上,以Monte Carlo法内嵌响应面法的模式具有良好的发展前景。通过吸收非线性学科的相关优秀算法作为高效率的响应面代理手段,将会极大地推动边坡动力可靠性分析方法的发展。
[1]陈祖煜. 土质边坡稳定分析:原理•方法•程序[M]. 北京:中国水利水电出版社,2003.
[2]DUNCAN J M. State of the art:limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,1996,122(7):577-596.
[3]DUNCAN J M,WRIGHT S G. Soil strength and slope stability[M]. Hoboken:John Wiley &Sons,Inc.,2005.
[4]ABRAMSON L W,LEE T M,SHARMA S,et al. Slope stability and stabilization methods[M]. New York:John Wiley &Sons,Inc.,2002.
[5]CRAIG R F. Craig's soil mechanics[M]. London:Spon Press,2004.
[6]CHENG Y M,LAU C K. Slope stability analysis and stabilization new methods and insight[M]. Abingdon:Routledge,2008.
[7]林育梁. 岩土与结构工程中不确定性问题及其分析方法[M]. 北京:科学出版社,2009.
[8]CRAWFORD C B,EDEN W J. Stability of natural slope in sensitive clay[J]. Journal of the Soil Mechanics and Foundations Division,ASCE,1967,93(SM4):419-436.
[9]JI J,LIAO H J,LOW B K. Modeling 2D spatial variation in slope reliability analysis using interpolated autocorrelations[J]. Computers and Geotechnics,2012,40:135-146.
[10]ZHANG J,ZHANG L M,TANG W H. New methods for system reliability analysis of soil slopes[J]. Canadian Geotechnical Journal,2011,48(7):1138-1148.
[11]HUANG J S,GRIFFITHS D V,FENTON G A. System reliability of slopes by RFEM[J]. Soils and Foundations,2010,50(3):343-353.
[12]GRIFFITHS D V,HUANG J S,FENTON G A. Influence of spatial variability on slope reliability using 2D random fields[J]. Journal of Geotechnical and Geoenvironmental Engineering,2009,135(10):1367-1378.
[13]GRIFFITHS D V,HUANG J S,FENTON G A. On the reliability of earth slopes in three dimensions[C]//Proceedings of the Royal Society A—Mathematical Physical and Engineering Sciences,2009,465(2110):3145-3164.
[14]LOW B K. Efficient probabilistic algorithm illustrated for a rock slope[J]. Rock Mechanics and Rock Engineering,2007,41(5):715-734.
[15]SHINODA M,HORII K,YONEZAWA T,et al.Reliability-based seismic deformation analysis of reinforced soil slopes[J]. Soils and Foundations,2006,46(4):477-490.
[16]陈祖煜. 水利水电工程风险分析及可靠度设计技术进展[M]. 北京:水利水电出版社,2010.
[17]TAN X H,WANG J G. Finite element reliability analysis of slope stability[J]. Journal of Zhejiang University(Science A),2009,10(5):645-652.
[18]LUO X F,LI X,ZHOU J,et al. A Kriging-based hybrid optimization algorithm for slope reliability analysis[J].Structural Safety,2012,34(1):401-406.
[19]LUO X F,CHEN T,LI X,et al. Slope safety factor search strategy for multiple sample points for reliability analysis[J]. Engineering Geology,2012,129:27-37.
[20]EL-RAMLY H,MORGENSTEM N R,CRUDEN D M.Probabilistic slope stability analysis for practice[J].Canadian Geotechnical Journal,2002,39(3):665-683.
[21]XU B,LOW B K. Probabilistic stability analyses of embankments based on finite-element method[J]. Journal of Geotechnical and Geoenvironmental Engineering,2006,132(11):1444-1454.
[22]PENG H S,DENG J,GU D S. Earth slope reliability analysis under seismic loadings using neural network[J].Journal of Central South University of Technology,2005,12(5):606-610.
[23]ZHAO H B. Slope reliability analysis using a support vector machine[J]. Computers and Geotechnics,2008,35(3):459-467.
[24]郑颖人,叶海林,黄润秋. 地震边坡破坏机制及其破裂面的分析探讨[J]. 岩石力学与工程学报,2009,28(8):1714-1723.ZHENG Ying-ren,YE Hai-lin,HUANG Run-qiu.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1714-1723.
[25]赵安平,冯春,李世海,等. 地震力作用下基覆边坡模型试验研究[J]. 岩土力学,2012,33(2):515-523.ZHAO An-ping,FENG Chun,LI Shi-hai,et al.Experimental research on seismic failure mode and supporting for slope of bedrock and overburden layer[J].Rock and Soil Mechanics,2012,33(2):515-523.
[26]叶海林,郑颖仁,杜修力,等. 边坡动力破坏特性的振动台模型试验与数值分析[J]. 土木工程学报,2012,45(9):128-135.YE Hai-lin,ZHENG Ying-ren,DU Xiu-li,et al. Shaking table model test and numerical analysis on dynamic failure characteristics of slope[J]. China Civil Engineering Journal,2012,45(9):128-135.
[27]徐光兴,姚令侃,李朝红,等. 边坡地震动力响应规律及地震动参数影响研究[J]. 岩土工程学报,2008,30(6):918-923.XU Guang-xing,YAO Ling-kan,LI Chao-hong,et al.Dynamic response of slopes under earthquakes and influence of ground motion parameters[J]. Chinese Journal of Geotechnical Engineering,2008,30(6):918-923.
[28]刘晓. 汶川地震区动力反应研究[博士学位论文 D]. 武汉:中国地质大学(武汉),2010.
[29]刘晓,唐辉明,胡新丽,等. 金鼓高速远程滑坡形成机制及动力稳定性[J]. 岩石力学与工程学报,2012,31(12):2527-2537.LIU Xiao,TANG Hui-ming,HU Xin-li,et al. Formation mechanism and dynamic stability of Jingu high-speed and long-run-out landslide[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(12):2527-2537.
[30]NEWMARK N M. Effect of earthquakes on dams and embankments[J]. Geotechnique,1965,15(2):139-160.
[31]祁生文,伍法权,刘春玲. 岩质边坡动力反应分析[M].北京:科学出版社,2007.
[32]张建海,范景伟,何江达. 用刚体弹簧元求解边坡、坝基动力安全系数[J]. 岩石力学与工程学报,1999,18(4):387-391.ZHANG Jian-hai,FAN Jing-wei,HE Jiang-da. Dynamic safety evaluation of slopes or dam foundations using rigid body-spring element method[J]. Chinese Journal of Rock Mechanics and Engineering,1999,18(4):387-391.
[33]张伯艳,陈厚群,杜修力,等. 拱坝坝肩抗震稳定分析[J]. 水利学报,2000,31(11):55-59.ZHANG Bo-yan,CHEN Hou-qun,DU Xiu-li,et al. Arch dam abutment aseismatic stability analysis[J]. Journal of Hydraulic Engineering,2000,31(11):55-59.
[34]薄景山,徐国栋,景立平. 土边坡地震反应及其动力稳定分析[J]. 地震与工程震动,2001,21(2):117-120.BO Jing-shan,XU Guo-dong,JING Li-ping. Seismic response and dynamic stability analysis of soil slopes[J].Earthquake Engineering and Engineering Vibration,2001,21(2):117-120.
[35]吴兆营,薄景山,刘红帅,等. 岩体边坡地震稳定性动安全系数分析方法[J]. 防灾减灾工程学报,2004,24(3):237-241.WU Zhao-ying,BO Jing-shan,LIU Hong-shuai,et al. A method for evaluating dynamic safety factor rock slope seismic stability analysis[J]. Journal of Disaster Prevention and Mitigation Engineering,2004,24(3):237-241.
[36]刘汉龙,费康,高玉峰. 边坡地震稳定性时程分析方法[J]. 岩土力学,2003,24(4):553-560.LIU Han-long,FEI Kang,GAO Yu-feng. Time history analysis method of slope seismic stability[J]. Rock and Soil Mechanics,2003,24(4):553-560.
[37]AL-HOMOUD A S,TAHTAMONI W W. A reliability based expert system for assessment and mitigation of landslides hazard under seismic loading[J]. Natural Hazards,2001,24(1):13-51.
[38]AL-HOMOUD A S,TAHTAMONI W W. Reliability analysis of three-dimensional dynamic slope stability and earthquake-induced permanent displacement[J]. Soil Dynamics and Earthquake Engineering,2000,19(2):91-114.
[39]RICE O C. Mathematical analysis of random noise[J].Bell System Technical Journal,1945,24:46-156.
[40]COLENMAN J J. Reliability of aircraft structures in resisting chance failure[J]. Operations Research,1959,7(5):639-645.
[41]杨仕教,罗辉,喻清,等. 高陡边坡爆破震动动力可靠性评价方法研究[J]. 武汉理工大学学报,2010,32(9):85-88.YANG Shi-jiao,LUO Hui,YU Qing,et al. Dynamic reliability evaluation method research on the vibration of blasting under the high and steep slope[J]. Journal of Wuhan University of Technology,2010,32(9):85-88.
[42]中华人民共和国国家质量监督检验检疫总局. GB6722-2003 爆破安全规程[S]. 北京:中国标准出版社,2004.
[43]刘红帅,唐立强,薄景山,等. 确定岩质边坡地震安全系数的新方法[J]. 哈尔滨工程大学学报,2009,30(9):1007-1010.LIU Hong-shuai,TANG Li-qiang,BO Jing-shan,et al.New method for determining the seismic safety factor of a rock slope[J]. Journal of Harbin Engineering University,2009,30(9):1007-1010.
[44]刘红帅,薄景山,杨俊波. 确定岩质边坡地震安全系数的简化方法[J]. 岩石力学与工程学报,2012,31(6):1107-1114.LIU Hong-shuai,BO Jing-shan,YANG Jun-bo.Simplified method for determing seismic safety factor of rock slope[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(6):1107-1114.
[45]唐辉明,李德威,胡新丽,等. 汶川地震区岩体稳定性评价技术方法[R]. 武汉:中国地质大学(武汉),2011.
[46]ALTAREJOS GARCIA L,ESCUDER BUENO I,SERRANO LOMBILLO A,et al. Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis[J]. Structural Safety,2012,36-37:1-13.
[47]BI R N,EHRET D,XIANG W,et al. Landslide reliability analysis based on transfer coefficient method:A case study from Three Gorges Reservoir[J]. Journal of Earth Science,2012,23(2):187-198.
[48]JOHARI A,JAVADI A A. Reliability assessment of infinite slope stability using the jointly distributed random variables method[J]. Scientia Iranica,2012,19(3):423-429.
[49]PARK H J,UM J G,WOO I,et al. Application of fuzzy set theory to evaluate the probability of failure in rock slopes[J]. Engineering Geology,2012,125:92-101.
[50]TAHA M R,KHAJEHZADEH M,EL-SHAFIE A.Application of particle swarm optimization in evaluating the reliability of soil slope stability analysis[J]Sains Malaysiana,2012,41(7):847-854.
[51]TANG X S,LI D Q,CHEN Y F,et al. Improved knowledge-based clustered partitioning approach and its application to slope reliability analysis[J]. Computers and Geotechnics,2012,45:34-43.
[52]CHEN C F,XIAO Z Y,ZHANG G B. Time-variant reliability analysis of three-dimensional slopes based on support vector machine method[J]. Journal of Central South University of Technology,2011,18(6):2108-2114.
[53]KHAJEHZADEH M,TAHA M R,EL-SHAFIE A.Reliability analysis of earth slopes using hybrid chaotic particle swarm optimization[J]. Journal of Central South University of Technology,2011,18(5):1626-1637.
[54]LI D Q,CHEN Y F,LU W B,et al. Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables[J]. Computers and Geotechnics,2011,38(1):58-68.
[55]LI D Q,JIANG S H,CHEN Y F,et al. System reliability analysis of rock slope stability involving correlated failure modes[J]. KSCE Journal of Civil Engineering,2011,15(8):1349-1359.
[56]LOW B K,ZHANG J,TANG W H. Efficient system reliability analysis illustrated for a retaining wall and a soil slope[J]. Computers and Geotechnics,2011,38(2):196-204.
[57]SAMUI P,LANSIVAARA T,KIM D. Utilization relevance vector machine for slope reliability analysis[J].Applied Soft Computing,2011,11(5):4036-4040.
[58]WANG Y,CAO Z J,AU S K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet[J]. Canadian Geotechnical Journal,2011,48(1):162-172.
[59]ZHANG J,ZHANG L M,TANG W H. Slope reliability analysis considering site-specific performance information[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(3):227-238.
[60]CHING J Y,PHOON K K,HU Y G. Observations on limit equilibrium-based slope reliability problems with inclined weak seams[J]. Journal of Engineering Mechanics,ASCE,2010,136(10):1220-1233.
[61]CHING J Y,PHOON K K,HU Y G. Efficient evaluation of reliability for slopes with circular slip surfaces using importance sampling[J]. Journal of Geotechnical and Geoenvironmental Engineering,2009,135(6):768-777.
[62]CHO S E. Probabilistic stability analyses of slopes using the ANN-based response surface[J]. Computers and Geotechnics,2009,36(5):787-797.
[63]HONG H P,ROH G. Reliability evaluation of earth slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering,2008,134(12):1700-1705.
[64]HSU Y C,LIN J S,KUO J T. Projection method for validating reliability analysis of soil slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering,2007,133(6):753-756.
[65]XUE J F,GAVIN K. Simultaneous determination of critical slip surface and reliability index for slopes[J].Journal of Geotechnical and Geoenvironmental Engineering,2007,133(7):878-886.
[66]JIMENEZ-RODRIGUEZ R,SITAR N,CHACON J.System reliability approach to rock slope stability[J].International Journal of Rock Mechanics and Mining Sciences,2006,43(6):847-859.
[67]BAFGHI A R Y,VERDEL T. Sarma-based key-group method for rock slope reliability analyses[J].International Journal for Numerical and Analytical Methods in Geomechanics,2005,29(10):1019-1043.
[68]GRIFFITHS D V,FENTON G A. Probabilistic slope stability analysis by finite elements[J]. Journal of Geotechnical and Geoenvironmental Engineering,2004,130(5):507-518.
[69]BHATTACHARYA G,JANA D,OJHA S,et al. Direct search for minimum reliability index of earth slopes[J].Computers and Geotechnics,2003,30(6):455-462.
[70]DUZGUN H S B,YUCEMEN M S,KARPUZ C A.Methodology for reliability-based design of rock slopes[J].Rock Mechanics and Rock Engineering,2003,36(2):95-120.
[71]GIASI C I,MASI P,CHERUBINI C. Probabilistic and fuzzy reliability analysis of a sample slope near Aliano[J].Engineering Geology,2003,67(3-4):391-402.
[72]TAN W H,CAI M F,ZHOU R D. Modified fuzzy point estimate method and its application to slope reliability analysis[J]. Journal of University of Science and Technology Beijing,2003,10(6):5-10.
[73]AUVINET G,GONZALEZ J L. Three-dimensional reliability analysis of earth slopes[J]. Computers and Geotechnics,2000,26(3-4):247-261.
[74]DODAGOUDAR G R,VENKATACHALAM G.Reliability analysis of slopes using fuzzy sets theory[J].Computers and Geotechnics,2000,27(2):101-115.
[75]MALKAWI A I H,HASSAN W F,ABDULLA F A.Uncertainty and reliability analysis applied to slope stability[J]. Structural Safety,2000,22(2):161-187.
[76]WANG J C,TAN W H,FENG S W,et al. Reliability analysis of an open pit coal mine slope[J]. International Journal of Rock Mechanics and Mining Sciences,2000,37(4):715-721.
[77]ZOU J Z,WILLIANS D J,XIONG W L. Search for critical slip surfaces based on finite element method[J].Canadian Geotechnical Journal,1995,32(2):233-246.
[78]陈昌富,龚晓南,王贻荪. 自适应蚁群算法及其在边坡工程中的应用[J]. 浙江大学学报(工学版),2003,37(5):566-569.CHEN Chang-fu,GONG Xiao-nan,WANG Yi-sun.Adaptive colony algorithm and its application to the slope engineering[J]. Journal of Zhejiang University(Engineering Science),2003,37(5):566-569.
[79]陈云敏,李育超,凌道盛. 蒙特卡洛法与有限元结合搜索边坡临界滑动面[J]. 岩土力学,2004,25(增刊2):75-80.CHEN Yun-min,LI Yu-chao,LING Dao-sheng. Locating critical slip surfaces by a method combining Monte Carlo technique and FEM[J]. Rock and Soil Mechanics,2004,25(Supp.2):75-80.
[80]陈云敏,魏新江,李育超. 边坡非圆弧临界滑动面的粒子群优化算法[J]. 岩石力学与工程学报,2006,25(7):1443-1449.CHEN Yun-min,WEI Xin-jiang,LI Yu-chao. Locating non-circular critical slip surfaces by particle swarm optimization algorithm[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(7):1443-1449.
[81]CHENG Y M,LANSIVAARA T,WEI W B. Twodimensional slope stability analysis by limit equilibrium and strength reduction methods[J]. Computers and Geotechnics,2007,34(3):137-150.
[82]CHENG Y M. Global optimization analysis of slope stability by simulated annealing with dynamic bounds and Dirac function[J]. Engineering Optimization,2007,39(1):17-32.
[83]LI Y C,CHEN Y M,ZHAN T L,et al. An efficient approach for locating the critical slip surface in slope stability analyses using a real-coded genetic algorithm[J].Canadian Geotechnical Journal,2010,47(7):806-820.
[84]WHITMAN R V. Evaluating calculated risk in geotechnical engineering[J]. Journal of Geotechnical Engineering,1984,110(2):145-189.
[85]张兴,廖国华. 多滑面边坡的破坏概率[J]. 岩土工程学报,1990,12(6):55-61.ZHANG Xing,LIAO Guo-hua. Failure probability of slope with multiple slip surfaces[J]. Chinese Journal of Geotechnical Engineering,1990,12(6):55-61.
[86]谭晓慧,王建国,胡晓军,等. 边坡稳定的模糊随机有限元可靠度分析[J]. 岩土工程学报,2009,31(7):991-996.TAN Xiao-hui,WANG Jian-guo,HU Xiao-jun,et al.Fuzzy random finite element reliability analysis of slope stability[J]. Chinese Journal of Geotechnical Engineering,2009,31(7):991-996.
[87]李典庆,周创兵. 考虑多失效模式相关的岩质边坡体系可靠度分析[J]. 岩石力学与工程学报,2009,28(7):542-551.LI Dian-qing,ZHOU Chuang-bing. System reliability analysis of rock slope considering multiple correlated failure modes[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(7):542-551.
[88]杨坤. 基于系统分析的漏天矿滑坡体系可靠度评价[J].山东科技大学学报(自然科学版),2009,28(4):9-12.YANG Kun. Reliability evaluation of landslip system in open-pit based on systems analysis[J]. Journal of Shandong University of Science and Technology(Natural Science),2009,28(4):9-12.
[89]吴振君,王水林,葛修润. LHS方法在边坡可靠度分析中的应用[J]. 岩土力学,2010,31(4):1047-1054.WU Zhen-jun,WANG Shui-lin,GE Xiu-run. Application of Latin hypercube sampling technique to slope reliability analysis[J]. Rock and Soil Mechanics,2010,31(4):1047-1054.
[90]LI K S,LUMB P. Probabilistic design of slopes[J].Canadian Geotechnical Journal,1987,24(4):520-535.
[91]MOSTYN G R,LI K S. Probabilistic slope analysisstate-of-play[C]//Proceedings of Probabilistic Methods in Geotechnical Engineering. Rotterdam:A. A. Balkema,1993:89-109.
[92]HASSAN A M,WOLFF T F. Search algorithm for minimum reliability index of earth slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering,1999,125(4):301-308.
[93]张明,刘金勇,麦家煊. 土石坝边坡稳定可靠度分析与设计[J]. 水力发电学报,2006,25(2):103-107.ZHANG Ming,LIU Jin-yong,MAI Jia-xuan. Reliability analysis and design of slope stability of earth-rock dam[J].Journal of Hydroelectric Engineering,2006,25(2):103-107.
[94]CRUM D A. Search algorithm for minimum reliability index of earth slopes—Discussion by Douglas A. Crum,Member,ASCE[J]. Journal of Geotechnical and Geoenvironmental Engineering,2001,127(2):194-195.
[95]D'ANDREA R. Search algorithm for minimum reliability index of earth slopes—Discussion by Robert D’Andrea,Member,ASCE[J]. Journal of Geotechnical and Geoenvironmental Engineering,2001,127(2):195-197.
[96]LI K S,CHEUNG R W M. Search algorithm for minimum reliability index of earth slopes—Discussion by K. S. Li,Member,ASCE,and Raymond W. M. Cheung[J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(2):197-198.
[97]吴振君,王水林,汤华,等. 边坡可靠度分析的一种新的优化求解方法[J]. 岩土力学,2010,31(3):713-718.WU Zhen-jun,WANG Shui-lin,TANG Hua,et al. A new optimization approach for slope reliability analysis[J].Rock and Soil Mechanics,2010,31(3):713-718.
[98]LOW B K,TANG W H. Efficient reliability evaluation using spreadsheet[J]. Journal of Engineering Mechanics,ASCE,1997,123(7):749-752.
[99]谢桂华,张家生,李继祥. 基于改进遗传算法的边坡可靠度分析[J]. 岩土力学,2009,30(6):1816-1820.XIE Gui-hua,ZHANG Jia-sheng,LI Ji-xiang. Slope reliability analysis based on improved genetic algorithm[J]. Rock and Soil Mechanics,2009,30(6):1816-1820.
[100]祝玉学. 边坡可靠性分析[M]. 北京:冶金工业出版社,1993.
[101]MOSES F,KINSER E. Analysis of structural reliability[J].Journal of Structural Division,1967,93(5):147-164.
[102]CORNELL C A. First-order uncertaintly analysis of soils deformation and stability[C]//Proceedings of First International Conference on Application of Statistics and Probability in Soil and Structure Engineering(ICAP1),Hong Kong:[s. n.],1971:129-144.
[103]DITLEVSEN O. Narrow Reliability bounds for structural systems[J]. Journal of Structural Mechanics,1979,7(4):453-472.
[104]谭晓慧. 边坡稳定可靠度分析方法的探讨[J]. 重庆大学学报(自然科学版),2001,24(6):41-44.TAN Xiao-hui. Discussion of reliability analysis methods of slope stability[J]. Journal of Chongqing University(Natural Science Edition),2001,24(6):41-44.
[105]吴震宇,陈建康,许唯临,等. 岩质边坡稳定的体系可靠度分析及工程应用[J]. 四川大学学报(工程科学版),2008,40(2):32-37.WU Zhen-yu,CHEN Jian-kang,XU Wei-lin,et al.Systematic reliability analysis of rock slope stability and its engineering application[J]. Journal of Sichuan University(Engineering Science Edition),2008,40(2):32-37.
[106]CHOWDHURY R N,TANG W H,SIDI I. Reliability model of progressive slope failure[J]. Geotechnique,1987,37(4):467-481.
[107]WU T H. Reliability analysis of slopes[C]//Reliabilitybased design in geotechnical engineering:computations and applications. New York:Taylor &Francis,2008.
[108]吴振君,葛修润,王水林. 考虑地质成因的土坡可靠度分析[J]. 岩石力学与工程学报,2011,30(9):1904-1911.WU Zhen-jun,GE Xiu-run,WANG Shui-lin. Reliability analysis of soil slope stability considering geologic origin[J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(9):1904-1911.
[109]贾厚华,贺怀建. 边坡稳定模糊随机可靠度分析[J]. 岩土力学,2003,24(4):657-660.JIA Hou-hua,HE Huai-jian. Analysis of fuzzy-random reliability of slope stability[J]. Rock and Soil Mechanics,2003,24(4):657-660.

