大型高速旋转机械基础单元结构件动力学相似设计的基础理论*
罗 忠 韩清凯 王德友 刘永泉
大型高速旋转机械基础单元结构件动力学相似设计的基础理论*
罗 忠 韩清凯 王德友 刘永泉
罗 忠 工学博 士 副教 授 110819 辽宁省 沈阳 市 东 北大 学 机械工 程与 自动 化学院 zhluo@mail.neu.edu.cn
韩清 凯 工学博 士 教授 116023 辽宁省 大 连市 大连 理工 大学 机械 工程 学院 hanqingkai@dlut.edu.cn 411201 湖南省 湘 潭市 湖南 科技 大学 湖南 省机 械装 备健康 维护 重点 实验室
王德 友 工学博 士 研究 员 110015 辽宁省 沈阳 市 沈 阳发 动机 设计研 究所 wangdy606@163.com
刘永 泉 工学博 士 研究 员 110015 辽宁省 沈阳 市 沈 阳发 动机 设计研 究所
在中国国家重点基础研究发展计划(973计划)项目《高端压缩机组高效可靠及智能化基础研究》、中国国家自然科学基金项目《旋转结构件模型试验的动力学相似理论及其应用研究》,中央高校基本科研业务费资助教育部新世纪优秀人才培育项目《混合式复杂转子系统动力学相似试验模型的设计方法研究》的共同资助下,针对大型高速旋转机械基础单元结构件,基于相似理论开展动力学相似设计理论研究,报告学术成果。
大型高速旋转机械基础单元结构件受转速、离心力、离心弯矩、恢复扭矩载荷、陀螺力矩和尺寸效应等因素的影响,仅依靠理论解析和数值模拟,不能彻底解决其动力学设计问题,必须增加物理试验验证。以弹性薄板为典型结构件,提出大型高速旋转机械基础单元结构件动力学相似试验模型设计方法。
通过分析基础单元结构件在结构振动测试试验中涉及的相似设计理论和方法,提出动力学相似定义——模型和原型在工作状态下,其动力学固有特性、模态振型、动力学响应行为,甚至包括典型故障特征,在一定范围内一致或成固定比例关系的相似现象。建立了基础单元结构件动力学相似设计的基本理论体系,包括完全相似试验模型设计准则及相似关系的建立方法,畸变模型的设计方法及畸变模型相似关系的修正方法。采用理论解析、数值模拟和试验验证相结合的研究方法,建立了模型与原型的结构参数、材料参数、载荷条件和边界条件成相似比例的映射关系,得到了4条动力学相似准则:相似模型和原型具有相同的模态主振型;完全几何相似的缩比模型和原型,其固有频率与几何缩比成反比;当缩比模型和原型为不同材料时,其固有频率正比于弹性模量和密度的缩比比值的平方根;通过附加质量块可以调整结构固有频率,也可能使模态次序发生较大变化。
相似模型试验可以有效物理模拟动力学特性及响应过程,再现原型的典型故障特征,由模型试验结果预测原型的动力学参数和特征。当模型参数和条件不能完全与原型成对应比例关系时,将导致基础单元结构件试验模型畸变,材料畸变和几何尺寸畸变是模型畸变的成因。从畸变产生机理出发,提出了模型畸变修正方法,以及模型几何适用区间确定方法。畸变模型修正存在一定的可修正区间,动力学相似模型几何适用区间与其误差控制区间及振型控制区间均相关,相似试验模型对于高阶动力学相似的参数设计要求更为严格。
以弹性薄板结构件为对象,以简化相似关系为目标,采用量纲分析法,提出弹性薄板完全几何相似和不完全几何相似模型(即畸变模型)与原型相似关系的建立方法。首先,利用解析及数值方法对弹性薄板固有特性问题进行参数敏感性分析,得到如下结论:弹性薄板不同振型对应的固有频率对几何尺寸变化的敏感性不同;弹性薄板振型中某一点的振幅对几何参数的敏感性与其相对位移有关;泊松比影响非常小,可以忽略不计且具有自相似性;材料并不是影响振动特性相似的主要因素,而几何尺寸是影响动力学相似的条件。其次,围绕建构畸变试验模型,推导了弹性薄板畸变模型的畸变系数;提出了弹性薄板构件畸变模型几何适用区间的确定方法;提出了一种基础单元构件的畸变模型修正方法——通过建立过渡模型的数值修正方程,获得动力学特性相似参数的修正系数,并对模型试验结果进行修正。研究表明,同种材料相似模型试验效果要好于异种材料相似模型的试验结果,缩比较大的模型,其试验结果好于缩比较小的模型的试验结果。
通过归纳,提出了动力学相似设计普适步骤,建立了大型高速旋转机械基础单元构件动力学相似设计理论框架,获得了动力学相似设计需要遵循的11项科学结论。
相似理论 动力学相似 相似准则 几何相似 大型高速旋转机械 基础单元结构件 弹性薄板 试验模型畸变模型畸变修正 数值拟合 模型几何适用区间 模型设计 量纲分析 固有特性 响应特性 集中质量 模态调节
1 引言
大型高速旋转机械(Large High-speed Rotating Machanical)的基础单元结构件(basic components),例如,转子叶片、转盘和转鼓,等等,其动力学特性及可靠性直接关系到装备的性能、寿命以及事故的预防。
受转速(rotating speed)、离 心 力 (centrifugal force)、离 心 弯 矩 (centrifugal moment)、恢 复 扭 矩 载 荷(restore torque load)、陀螺力矩(gyroscopic moment)和尺寸效应(size effect)等因素的影响,仅靠理论解析和数值模拟,并不能彻底解决大型高速旋转机械基础单元结构件动力学问题。这是 因为理论解析常 是基 于某些假设开展数学推导,而数值模拟往往忽略一些影响因素,因此必须通过物理试验来进一步验证与考察。
在工程实践中,直接采用结构原型进行试验,存在几何尺寸、旋转台动力、实验空间、试验难度、试验成本等约束,困难较多。采用动力学相似 模 型试 验(Dynamic Similitude Test Model),不 仅可 以合理 调整结 构、材料和工艺,还可以人为控制主要影响因素,剔除次要影响因素,降低试验难度,缩短试验周期。
因此,通过相似模型试验,物理性模拟基础单元结构件动力学特性及响应过程,复现基础单元构 件原 型的典型故障特征,再由模型试验结果预测基础单元构件原型的动力学参数和特征,具有重要的理论研究价值和工程应用价值。
1.1 相似理论的起源
自17世纪开始,相似理论(Similarity Theory)的研究 和应 用已有过许 多先 驱性的工作。1638 年,伽 利略(Galileo Galilei)在《关 于 两 门新科学 的 对 话》(Mathematical Discourses Concerning Two New Sciences Relating to Mechanicks and Local Motion)中说明[1],威尼斯人在比照相似的小船 而建 造大船时发现,桅 柱如只按几何尺寸简单放大则强度不够;事实上,如果物体尺寸减小,其强度并不按相同比例减小,物体越小其相对强度越大。这一论述已经深入到相似理论的实质问题,一般认为这是相似理论的最早萌芽。
1686年,牛顿(Isaac Newton)在对其第三定律(Newton's Third Law)的表 述和 论证时就完全是 采用 两个物体作相似运动来说明的;之后,牛顿又提出被称为牛顿数(Newton Number)的相似准数(Similarity Criterion)[2];1741年前后,英国进行炮舰的水池拖拽试验,这 是相 似理论最早的实 践应用[3-4];1872年,英国 学者弗洛德(Willian Froude)根据船模试验提出相似准数[5];1900年,莱特兄弟(Wright brothers)进行了风 洞试验[6]。
相似理论和其他科学理论一样,都是随着社会生产需要,基于基础科学和有关相邻学科理论,以及观察、实验和测量等技术的发展而发展起来的,许多著名学者在相似理论领域都创造出了成就。
1.2 相似理论及相似设计方法研究与发展
1848年,法国科学家贝特朗(Bertrand J)定义了相似准数这一概念[7]。
【相似准数】 由确定物理现象的物理量组成反映现象物理相似数量特征的无量纲数群。
之后,以三大基 本定理[8]为基 本框架 和理论 基础,逐 步建立 起经典 相似理 论(The Classical Similarity Theory)。
贝特朗于1868年以力学方程分析为基础,建立了相似第一 定理(The First Similarity Theorem)[9],描述了相似现象的基本特性,把相似现象正式提升到理论高度。
【相似第一定理】 对于相似现象,其相似指标等于1,或其相似准则的数值相等。
1914年,白金汉(Buchinghan E)[10]提出 了相似 第二 定 理(The Second Similarity Theorem),用以 分 析相似现象中各物理参量的表达方法。
【相似第二定理】 设描述一个物理现象的函数关系中包含n个物理量,其中有m个物理量的量纲是相互独立的,则该现象具有(n-m)个相似准则,且描述此现象的函数关系式可表达成(n-m)个相似准则间的函数关系式。
1931年,前苏联学者库克曼(Gukhman AA)提出了相似第 三定理(The Third Similarity Theorem)[11],回答了现象相似的充分必要条件,使相似理论得到进一步完善。
【相似第三定理】 对于同一类物理现象,如果单值量相似,而且由单值量所组成的相似准则在数值上相等,则现象相似。
需要指出的是,相似理论三大定理只定义了在什么条件下物理现象相似,或者由物理现象相似可以得出什么样的相似准则及其相似关系,而没有给出具体的推导方法。
此后,学者们基于经典相似理论对相似理论开展了更加深入的研究,提出了量纲分析法(Dimensional Analysis),方程分析法(Equation Analysis)和定律分析法(Law Analysis)等相似分析方法[12-13]。
对于量纲分析法,Vaschy A在大约1896年得到了π定理(The Theorem ofπ)[14]的基本形式。但直到1914年,白金汉发表了具有严格意义的π定理后,量纲分析法才逐渐被承认,在工程领域得到广泛的应用。
1915年,瑞利(Rayleigh J)[15]采用量纲分析法研究两个相似物理现象,建立起第一个相似试验模型,成为量纲分析法在工程应用方面的先驱。事实上,此后广泛采用的量纲分析法,均是以Rayleigh提出的物理方程量纲一致性原理(Dimensional Consistency Principle)为基础发展起来的。
第一个单值表征基本物理现象的无量纲组合量是雷诺(Reynolds O)引进的雷诺数(Reynolds Number)[16]。雷诺数是一个重要的相似准则数,达到同样雷诺数的不同流场性质相似。
Goodier[17-18]将相似理论引入结构振动系统的研究之中,并系统地研究了利用量纲分析法建立两个结构系统之间的相似条件。从此以后,许多学者对相似理论中的量纲分析法不断进行完善与发展[19-24],使之成为相似理论研究中比较重要的研究方法。
中国学者谈庆明[25]于2005年出版了专著《量纲分析》,介绍了量纲分析法在力学领域里的应用。杨俊杰[26]、徐挺[27]、周美立[28]等学者也以量纲分析法为基础,针对相似原理在工程中的应用出版了各自的著作。
量纲分析法在处理简单物理现象或简单结构体时比较简单方便。在处理复杂物理现象或复杂结构体时,正确选择物理量是非常困难的事情。由于无法建立与其相应的量纲方程,很难导出正确的相似条件结论,并且这种方法的成功应用还依赖于分析者选择无量纲项的技能。
在量纲分析法得到发展的同时,方程分析法也逐渐得到应用。Kline[29]论述了方程分析法的应用前景,并将方程分析法应用于求解结构振动的相似条件。Szücs[30]将方程分析法应用到热学、流体力学、弹性力学等领域,利用方程分析法得出两个物理现象之间的相似条件和相似关系。Qian[31-32]等学者利用方程分析法得到多层复合板之间的相似条件,并对加载冲击力的模型复合板进行了试验研究,预测了原型复合板的特性。
由于方程分析法与量纲分析法各有特点,针对工程问题各自也显示了其优势,因而在相似性设计中主要采用这两种方法。
定律分析法的依据是支配相似现象的物理定律相同,由分析支配现象的物理定律得出相似准数。这种方法要求对所研究的现象运用已掌握的全部物理定律,并能辨别其主次,一旦这个要求得到满足,解决问题并不困难,而且还可获得数量足够的、反映现象实质的π项。但这种方法的缺点是只是就事论事,看不出现象的变化过程和内在联系,故作为一种方法,缺乏典型意义,再加之由于必须要找出全部物理定律,所以对于未能全部掌握其机理的、较为复杂的物理现象,运用这种方法是不可能的,所以其应用偏少。
对比相似理论的三大常用分析方法,可以发现以下特点。
(1)量纲分析法在分析复杂物理现象或复杂结构体时,物理量的正确选择是建立与其相应的量纲方程并导出正确相似结论的关键;由于量纲分析法不能区别量纲相同但在方程中物理意义不同的量,将会导致错误的结果。
(2)方程分析法结构严密,能够反映物理现象中最为本质的物理定律,结论可靠,但它需要建立能反映物理现象的微积分方程,要求对所研究的物理现象的机理有充分的认识,故而方程分析法对于研究未知现象的相似关系存在若干困难。
(3)定律分析法要求了解支配现象的物理定律,而在大多数情况下,尤其是实际工程中,物理定律的应用范围具有一定的局限性。所以定律分析法不够灵活,优势不明显,应用不广泛。
1.3 工程材料及结构的动力学相似理论研究现状
相似模型理论和技术在20世纪40-70年代期间几乎失去曾经的辉煌,直到20世纪70年代后期又开始逐渐成为学者们的研究热点,重新应用于航海试验、风洞试验、航空应用、地震工程和液压设备的性能试验。
从Goodier[17-18]利用量纲分析法建立两个结构系统之间的振动特性相似条件开始,人们逐步利用相似理论开展结构振动特性的研究。
在板类结构相似模型设计方面,Morton[33]利用π定理推导冲击响应完全相似关系,通过放宽厚度相似关系和应变率相似关系分别对冲击未破坏和冲击破坏等情况进行实验验证。Singhatanadgid[34]等学者推导了反对称层合板固有频率畸变模型的相似关系。Ungbhakorn[35]等学者利用平衡方程建立了薄板畸变模型的相似关系,并对不同畸变条件下相似关系的预测准确性进行了研究。Jha[36]等学者使用量纲分析法进行相似性设计时的重力效应及采用附加质量对悬臂梁模型的修正方法。Songkhla[37]等学者对薄板完全相似模型及材料畸变模型的动力特性相似关系进行了实验验证,探索不同边界条件对模型预测结果的影响。
在壳类结构相似模型设计方面,Ungbhakorn[38-39]等学者报告了对称及反对称铺层复合材料层合柱壳畸变模型的设计方法。Kee[40]等学者基于Reissner-Mindlin假设建立带预扭型的复合材料层合壳叶片模型,考虑了惯性力、科氏力的影响,通过有限元方法计算了叶片的动力特性。Torkamani[41]等学者运用平衡方程法建立圆柱筒的相似关系,对带筋板的圆柱筒采用等效刚度法建立了相似模型,并通过实验对相似模型的预测效果进行了验证。Bijan[42]等学者讨论了单一材料(铝)与不同铺层复合材料层合圆柱壳的等效设计,针对其塑性变形问题,通过理论分析与实验给出了材料的等效设计方法。Murugan[43]等学者利用量纲分析法分析了不同材料悬臂板的弯曲及动力相似,用ANSYS对核反应堆顶板相似关系进行了仿真分析及验证,并通过有机玻璃实验模型进行了验证。
Krayterman[44]等学者根据量纲分析法推导出平板和圆筒的相似准则和相似关系,建立了相似模型,考虑了边界条件对相似条件的影响,讨论了相似方法的精度。Simitses和Rezaeepazhand等学者[45-52]利用相似理论研究了复合材料的多层结构的振动响应性质,提出利用相似模型试验可以预测原型复合材料的特性。
Soedel[53]利用方程分析法推导出了振动薄壳的精确相似准则和近似相似准则。他通过对薄壳的Love方程进行分析,讨论了两种情况下的相似准则,一是当拉伸效应占主导作用时,弯曲效应可以忽略,圆筒的固有频率的相似关系与厚度的相似条件没有关系;二是当弯曲效应占主导地位时,圆筒的固有频率的相似关系与圆筒厚度的相似条件成正比。他还对振动响应和负载的相似性进行了研究,但是,他在文献中没有考虑结构阻尼和流体负载对于相似关系和相似条件的影响。
Chouchaoui[54]等学者研究了圆壳管在拉伸、扭转、弯曲,以及内外压力等作用状态下的相似模型,通过相似模型推算其弹性力学行为和振动响应。Wu[55-57]等学者利用相似理论研究了平板振动响应的相似设计问题,他针对二维全尺寸原型板的动载振动特性,利用相似梁模型进行了推算。Wu[58]和Young[59]分别以转子-轴承系统为对象,针对模型推算全尺寸原型结构问题进行了研究,采用量纲分析法和方程分析法相结合的方法研究了系统质量、刚度、阻尼和外载对振动特性影响的相似性推算问题,但并没有考虑旋转状态(转速、陀螺力矩和质量效应,等等)的影响。
在中国,相似理论在土木工程和建筑结构的抗震性能和模型试验中应用较多,应用成果相对也比较成熟。
林皋[60]和迟世春[61]等学者分别针对评价建筑结构的抗震性能、地震破坏机理,以及建筑结构动力模型试验的相似技巧等问题进行了研究,还研究了大型水下地震模拟系统。
1996年,吕西林教授针对高层建筑结构模型抗震试验,开展了结构模型试验的动力学相似理论研究,构建了模型结构和原型结构之间在不同变形阶段的各种动力学相似关系,提出了用模型试验结果推算原型结构性能的方法和消除误差的途径,研究成果对于结构抗震模型动力试验和计算分析具有指导意义。
围绕相似理论在结构振动试验方面的应用,雷正保[62-63]等学者针对大位移、弹塑性的结构振动等问题,运用量纲分析法导出了动态大位移大转角弹塑性相似结构的相似关系,应用算例证明了相似理论解决这类问题的可行性。李少华[64]等学者提出了一种较为实用的复合材料颤振模型设计方法,该方法采用部分结构相似颤振模型设计策略,在动力相似模型的基础上,增加了对主要受力构件和蒙皮的布置及传力路线的模拟,可以提高模型刚度分布和质量分布的模拟精度,进而提高振动特性和颤振特性的相似程度。胡培民[65]针对转子扭转振动特性相似模型试验进行了基础性分析,指出对于一个转子,若将其径向尺寸缩小到原来的(1/Kd),轴向尺寸缩小到原来的(1/KL),按相同或不同的材料制作成相似模型,则相似模型扭转振动的频率特性曲线和实际转子的频率特性曲线相似,两者固有频率之间具有确定的相似关系,并且和径向尺寸缩小的比例Kd无关,两者的振型完全相同之结论。
刘尔重[66]针对复合材料圆柱壳体缩比件进行推导,得出了相似判据,并通过试验测量证明了判据的正确性,说明相似判据可以用在复合材料结构件应力的实验分析。晏砺堂[67]和王德友[68]基于航空发动机的转子碰摩振动特性的研究,设计了模型转子系统,通过实验模拟了发生碰摩故障。通过实测振动特性与理论分析的结果比较,得到了良好的一致性,说明了相似模型在实验模拟应用的可行性。
1.4 相关讨论与思考
对比国内外相似理论及其在结构振动试验中的应用研究现状,可以得到以下结果。
(1)相似理论起源虽早在17世纪,但最初只是简单的大小对比关系,以及提出一些基础性概念,并没有深入细致研究。直到20世纪提出了相似第二定律和第三定律,才真正开启了相似理论的研究。
(2)继瑞利采用量纲分析法建立起第一个相似试验模型之后,基于相似第二定理的量纲分析法在工程实践中逐渐开始广泛应用。量纲分析法简单方便,但是在复杂情况下,不能建立完整的量纲方程,进而导致相似关系推出不完整性结论。相对而言,方程分析法因其严密,更能被人们所接受。但由于要求对于所研究对象的工作机理有充分的认识,导致了其应用范围狭小,往往不方便应用。
(3)在中国,开始开展动力学相似研究主要集中在桥梁等大型结构,林皋和迟世春等学者的研究为研究构件动力学相似提供了理论参考。国外学者在基础单元结构件方面进行的大量研究并取得了很好的成果。近年来,国内学者也开始将相似理论应用到结构件的设计。郝燕平[69]对叶轮机叶片特别是压气机叶片所涉及的静力学相似、振动特性相似和动力响应相似等结构相似性问题进行了理论研究,初步研究了在保持气动相似条件下,模型叶片和原型叶片之间的静强度、振动特性、振动响应的相似性问题,给出了对应的相似准则。
(4)相对于气动相似理论的普遍应用,在大型机械中,结构相似理论的应用研究很少,其主要原因是由于相对于气动相似而言,结构相似的影响因素要复杂得多,机械结构相似难以如同气动相似那样可归结为统一的相似参数。
(5)面对越来越高的技术要求,对于结构振动试验中的相似设计理论与方法的研究仍然比较粗略。通过深入研究基础单元结构件在振动测试试验中相似设计理论和方法,将为建立模型结构推算方法、再现原型结构的振动特性和故障特征、寻找消除误差的途径提供重要依据,是目前急需的基础性工作,有较强的理论和技术需求。
1.5 研究对象和研究方法
针对大型高速旋转机械基础单元结构件动力学相似设计的要求,考虑到弹性薄板结构的普适性及典型性,以弹性薄板为研究对象,分析其动力学相似模型的设计方法。首先通过量纲分析法与方程分析法建立弹性薄板的动力学完全相似模型,研究通过集中质量进行模态调节的方法;在此基础上,对其几何尺寸、材料不完全相似的畸变模型进行分析,运用理论分析和数值分析讨论畸变模型的设计方法,误差分析及误差修正等问题;最后通过实验对弹性薄板动力学相似模型的适用性进行实验验证,并提炼相关科学结论,研究路线见图1。
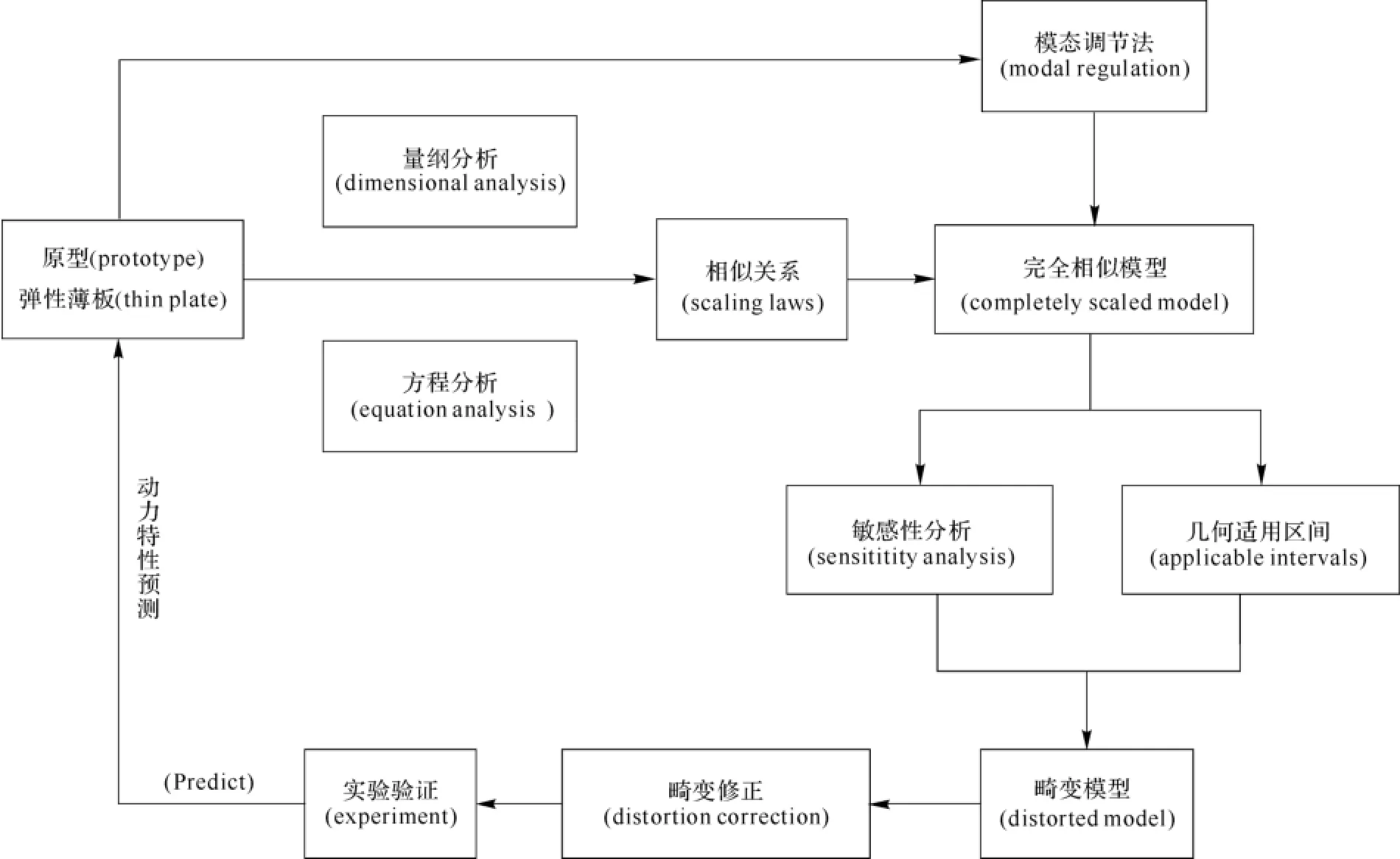
图1 研究路线Fig.1 Chart of research process
2 相似性设计基本理论
在科学研究和工程实践中,物理实验是一个重要环节。物理实验包括直接实验法(direct experimentation method)和模型实验研究法(model test method)等两类实验方法。直接采用原型进行实验存在很大的局限性,例如,几何尺寸的限制、动力和空间的限制、实验难度的限制、实验成本的限制,等等。
采用动力学相似模型(dynamic similarity model)实验,不仅可以合理调整结构、材料和工艺,大幅降低实验成本,而且可以人为控制主要影响因素,剔除次要影响因素,降低实验难度,缩短实验周期。这其中,动力学相似模型设计至为重要。
2.1 相似模型
【定义1a 原型(prototype)】 需要进行相关测量和分析,并最终在工程中进行应用的工程结构。
【定义1b 模型(model)】 为便于进行实验而设计的,能够通过实验数据对原型进行分析预测的基础结构。
模型与原型具有如下关系:
(1)原型通常结构较复杂或体积较大(较小),难以通过实验来获取相关数据;模型通常结构简单,便于实验。
(2)模型实验通常不能够反映原型的所有性能;针对原型分析不同问题,需选择不同的模型结构进行实验。
(3)原型与模型的性能实验数据,需要通过一定形式的数学表达式建立联系。
【定义1c 相似现象(similar phenomenon)】[70]遵循同一物理方程的两个同类现象对应的物理量成比例。
若物理量y*,x*,X*满足以下关系。y*=f(x*,X*)(1)式中,y*为系统输出物理量;x*为系统输入物理量;X*为影响系统输出的系统物理量。
则有

2.1.1 几何相似
【定义2a 线性长度(linear length)】 物体上两点之间的直线距离,如直径、半径、宽度、深度、高度、中心距,等等。
模型物体与原型物体的几何尺寸相似包括长度相似、面积相似和体积相似,其直接参数体现为线性长度。线性长度属于一维方向的物理量。
【定义2b 长度相似比(length similitude ratio)】 模型物体几何尺寸的线性长度与原型物体几何尺寸的线性长度比值。
长度相似比

式中,CL为模型物体与原型物体的长度相似比;Lm为模型物体几何尺寸的线性长度;Lp为原型物体几何尺寸的线性长度。
【定义2c 面积(area)】 物体表面或封闭图形的大小。
【定义2d 面积相似比(area similitude ratio)】 模型物体几何尺寸与原型物体几何尺寸的面积比值。
面积相似比

式中,CA为模型物体与原型物体的面积相似比;Am为模型物体某面的几何尺寸;Ap为原型物体某面的几何尺寸。
【定义2e 体积(volume)】 物质或物体所占据空间或所占据容积。
【定义2f 体积相似比(volume similitude ratio)】 模型物体几何尺寸与原型物体几何尺寸的体积比值。
体积相似比

式中,CV为模型物体与原型物体的体积相似比;Vm为模型物体几何体积值;Vp为原型物体几何体积值。
【定义2 几何相似(geometric similarity)】 模型物体几何形状和原型物体几何形状及几何尺寸相似——模型物体和原型物体的外形完全一致,对应长度、面积、体积等几何特征之比值为一个定值。
2.1.2 运动相似
运动是指物体的运动,而物体的运动需要时间,故此,运动时间在物体运动相似中是一个非常重要的物理参量。
【定义3a 时间相似比(time similitude ratio)】 模型物体运动时间与原型物体运动时间的比值。

式中,Ct为模型物体与原型物体的运动时间相似比;tm为模型物体在运动过程中的时间值;tp为原型物体在运动过程中的时间值。
【定义3b 速度(velocity)】 物体在单位时间内的运动距离。
【定义3c 速度相似比(velocity similitude ratio)】 模型物体运动时间与原型物体运动时间的比值。速度相似比

式中,Cv为模型物体与原型物体的速度相似比;vm为模型物体的运动速度;vp为原型物体的运动速度。
【定义3d 加速度(acceleration)】 物体运动速度在单位时间内变化量。
【定义3e 加速度相似比(acceleration similitude ratio)】 模型物体运动加速度与原型物体运动加速度的比值。
加速度相似比

式中,Ca为模型物体与原型物体的加速度相似比;am为模型物体的加速度值;ap为原型物体的加速度值。
【定义3 运动相似(kinematic similarity)】 在整体相似现象中,模型物体运动参数(速度、加速度、位移等)和原型物体运动参数两者相比,矢量参数保持方向一致、大小成比例,标量参数保持大小成比例的相似现象。
2.1.3 动力相似
动力相似中的“动力”应理解为物体运动或静止时的受力,力为矢量,具有大小和方向。
【定义4a 受力相似比(stress similitude ratio)】 模型物体所受外力与原型物体所受外力大小的比值。受力相似比

式中,CF为模型物体与原型物体的受力相似比;F1m,F2m,…,Fn′m为模型物体在各个方向上的受力大小; F1p,F2p,…,Fn′p为原型物体在各个方向上的受力大小。
在讨论模型物体与原型物体的受力相似比时,需要保证受力方向相同,才有大小的比值。同时,物体所受合力的大小与同名力(对应边)的比值一致。
【定义4 动力相似(stress similarity)】 在运动相似系统中,模型和原型中对应点上作用的各同名力矢量互相平行,且其大小具有同一比值——模型物体和原型物体中任意对应点的力多边形相似,对应边(同名力)成比例(见图2)。
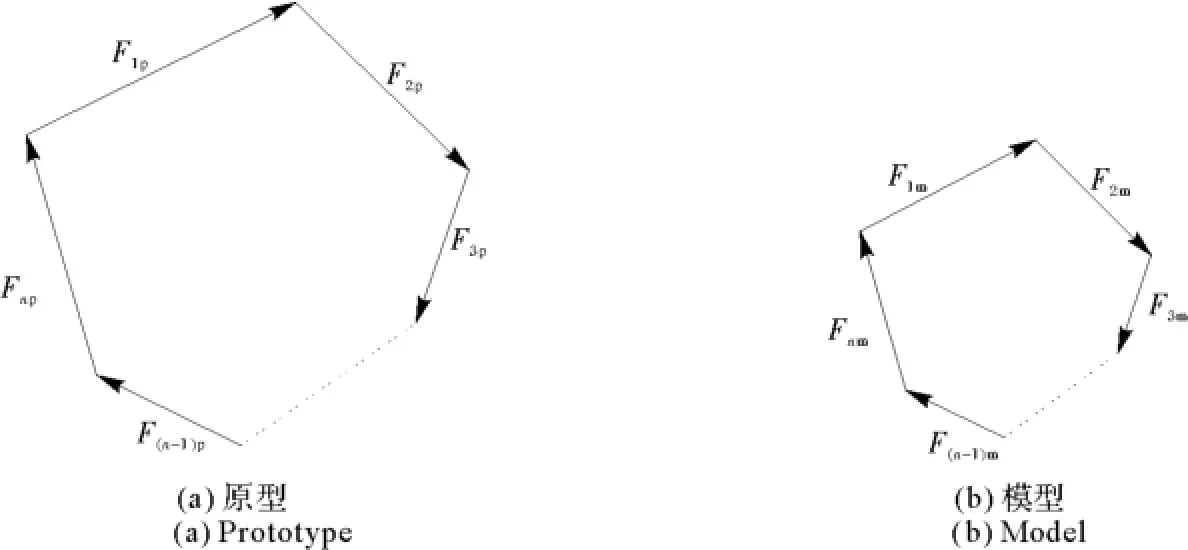
图2 动力相似示意Fig.2 Schematic diagram of dynamic similarity
2.1.4 动力学相似
【定义5a 固有频率(natural frequency)】 物体做自由振动时,其位移随时间按正弦规律变化,振动的频率与初始条件无关,而与系统的固有特性有关。
【定义5b 固有频率相似比(natural frequency similitude ratio)】 模型物体固有频率与原型物体固有频率的比值。

式中,Cω为模型物体与原型物体的固有频率相似比;ωm为模型系统固有频率;ωp为原型系统固有频率。
【定义5c 刚度(stiffness)】 弹性体抵抗变形(弯曲、拉伸、压缩等)的能力。
【定义5d 刚度相似比(stiffness similitude ratio)】 模型物体刚度与原型物体刚度的比值。

式中,CK为模型物体与原型物体的刚度相似比;Km为模型物体刚度;Kp为原型物体刚度。
质量是描述物体所含物质多少的物理量,质量不随物体的形状和空间位置的改变而改变,是物质的基本属性之一。
【定义5e 质量相似比(mass similitude ratio)】 模型物体质量与原型物体质量的比值。

式中,CM为模型物体与原型物体的质量相似比;Mm为模型物体质量;Mp为原型物体质量。
对于质量-弹簧系统(见图3),其自由振动固有频率相似比
式中,Ksm为模型弹簧刚度;Ksp为原型系统弹簧刚度;Msm为模型弹簧质量;Msp为原型弹簧质量;CKs为模型物体与原型物体的刚度相似比;CMs为模型物体与原型物体的质量相似比。
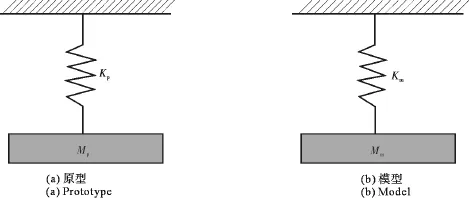
图3 质量-弹簧系统Fig.3 Mass-spring system
【定义5 动力学相似(dynamical similarity)】 为了达到模型物体和原型物体在工作状态下的固有特性、模态振型、动力学响应行为,甚至包括典型故障特征等在一定范围内一致或形成固定比例关系,而使建立的模型物体与原型物体的结构参数、材料参数、载荷条件和边界条件成比例映射关系的相似现象。
需要注意的是,模型和原型的动力学相似,除了受到以上3个相似条件(几何相似、运动相似和动力相似)的影响和制约之外,还受到边界条件和初始条件的影响。
2.2 相似模型设计
2.2.1 白金汉π定理
【白金汉π定理(BuckinghamπTheorem)】 对于某个物理现象可给出的无量纲综合数群(相似准数)的个数,等于影响该现象的全部物理量的个数减去用以表达这些物理量的基本量纲个数。
如若某个物理现象含有n个具有影响的物理量,则该物理现象可以表示为如下形式。

式中,^x1为影响物理现象的第一个物理量;^x2为影响物理现象的第二个物理量;^xn为影响物理现象的第n个物理量;f(·)为n个物理量的关系表达式。
根据白金汉π定理,如果这n个物理量包含m个基本量纲,则该物理现象可以进一步表示为如下形式。

式中,π1为第一个非基本量纲;π2为第二个非基本量纲;πn-m为第(n-m)个非基本量纲;m为基本量纲个数。
白金汉π定理描述了物理现象中所有物理量与无量纲参数之间的数量关系。一般来说,具有描述物理现象的普遍意义。
2.2.2 相似准数
根据相似理论,在保持几何相似前提下,两个规模不同的运动保持相似的条件是,所有对运动有影响的无量纲组合量必须保持对应相等。
这些对运动有影响的无量纲组合量可以看成是一个综合数群(comprehensive group)。为此,可以根据综合数群来判断模型与原型是否相似。
【定义6 相似准数(similarity criterion)】 用于判断模型与原型是否相似,由确定物理现象的物理量组成的反映现象物理相似数量特征的无量纲数群体。
对于一个相似模型和原型系统(见图4),为了满足保证相似,模型与原型的相应物理量之间必须满足一定的约束条件。

图4 相似模型和原型示意Fig.4 Schematic diagram of similar model and prototype
以匀速运动为例,原型与模型之间必须满足以下条件。

式中,vm为模型物体速度;vp为原型物体速度;Cv为速度相似常数;sm为模型物体位移;sp为原型物体位移; Cs为位移相似常数;tm为模型物体运动时间;tp为原型物体运动时间;Ct为时间相似常数。
根据匀速运动的特点,若要保证原型与模型之间相似,则必须满足以下条件。

根据式(17),要得到运动相似,则需要保证各个运动参量的相似比一定。上述过程中,涉及的各个参量(sm,sp,vm,vp,tm,tp)表征了特定的物理效应。
相似准数分为两类,一类是直接地反映某一基本现象的内部规律的,称为原始准数(或基本准数)(basic number of quasi);另一类是经过理论推导获得,反映了相似模型和原型之间两个基本现象的相互关系,称为关联准数(或导出准数)(derivation number of quasi)。
对于复杂机械结构的动力学相似问题,应根据现象本质分析,导出其所包含的基本准数,同时要把其中的某些基本准数转化成反映基本现象间相互关系的导出准数,继而获得描述复杂现象的一般性准数方程,这个准数方程即为相似关系(scaling laws)[71]。
2.2.3 自相似性
【定义7 相似参数(similarity parameter)】 可以通过描述物理现象的方程式或函数式,利用相似转换得到各参数对应的相似关系或相似条件的参数。
【定义8 非相似参数(dissimilarity parameter)】 在工程应用中,由于受到材料属性或加工能力等方面的限制,而不能够满足模型和原型之间相似关系的参数。
非相似参数对相似理论的应用将产生限制,破坏相似条件。例如,在分析机械结构的模型和原型动力学相似时,泊松比μ是一个非相似参数,其原因是在满足其他相似参数成比例关系时,要求相似模型材料和原型材料的泊松比μ也成固定比例,这极难做到。
非相似参数μ的存在,意味着要使原型和模型的现象保持相似,两者的材料只能相同,即材料相同是相似的必要条件,这就大大限制了模型设计时材料的选用范围,使相似理论的应用范围受到了限制。
为了解决由于非相似参数带来的不便,需要引入了自相似概念。
【定义9 自相似(self-similar)】 如果任何一个已定相似准则在其某一数值范围内变化,而现象的相似性实际并不被破坏的相似现象。
【定义10 自相似性(self-similarity)】 具有自相似现象的结构或系统。
【定义11 自相似区(self-similar area)】 在满足相似准则条件下,使结构或系统具有自相似性的相应相似参数的数值范围。
对于机械结构动力学相似分析,由于不同材料的泊松比数值相差很小,如绝大多数材料的泊松比都在0.3左右,故材料参数泊松比μ具有自相似性,即泊松比在一定范围内变化时,其对动力学特性的影响不大。
2.2.4 畸变模型
【定义12 畸变(distortion)】 模型外形尺寸、材料、边界条件,不遵守相似准则而发生变化的现象。
【定义12a 畸变模型(distorted model)】[72]在白金汉π定理描述中,当相似模型和原型的所有π项中有一个或几个起支配作用的模型设计条件不能被满足时,所得到的相似模型。
由白金汉π定理可得如下判别准则。
【判别准则1】 未发生畸变的模型(完全相似模型)和原型,满足以下判别准则。

【判别准则2】 发生了畸变的相似模型,满足以下判别准则。

在进行相似模型设计时,常常会有一些物理量不能满足相似关系要求,如进行转子叶片试验模型设计时,其几何尺寸(长度、宽度和厚度)的缩比将不尽相同——发生了畸变,此时利用模型试验结果来预测原型特性时,需要进行畸变修正。
如若引入畸变修正系数φk,则判别准则需满足以下形式。
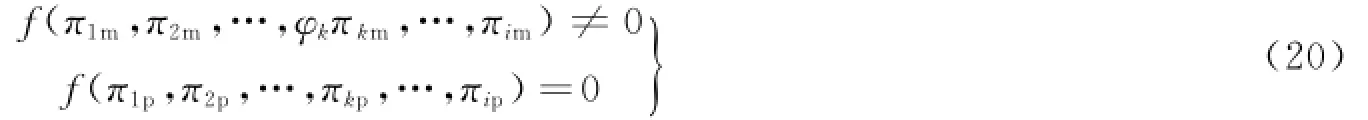
一般来说,产生模型畸变有以下原因[73]。
(1)尺寸畸变 由于设计试验模型的结构要求或强度要求等因素造成的尺寸畸变。例如,原来模型的长宽比满足的相似关系是一个比例常数,但由于模型结构设计需要在加工过程中使得长宽比不等于原设计的常数。
(2)载荷畸变 一是载荷不能按模型设计条件所要求的比例增加;二是加载前模型与原型在几何上是相似的,但加载后由于构件的变形情况不同,使二者在几何参量上失去相似性。
(3)材料畸变 在相似模型和原型的泊松比不同的情况下,材料将在弹性上产生畸变,这一点对沿轴向应力来说没有影响,但对切向应力的影响较大。
2.3 相似关系的建立方法
建立相似关系的方法主要有量纲分析法(dimensional analysis)、方程分析法(equation analysis)和定律分析法(law analysis)等3种。
量纲分析法的主要理论依据是相似理论第二定理,即由分析影响现象的主要物理量的量纲得出相似准数。它对相关物理量的因次(量纲)进行分析,得到为数较少的无量纲参数群之间关系。
方程分析法的理论依据是相似现象的物理方程相同,由分析描述现象的方程得出相似准数。
定律分析法的理论依据是支配相似现象的物理定律相同,由分析支配现象的物理定律得出相似准数。
实际应用中,常用的是量纲分析法和方程分析法,定律分析法应用很少。系统相似关系建立流程见图5。
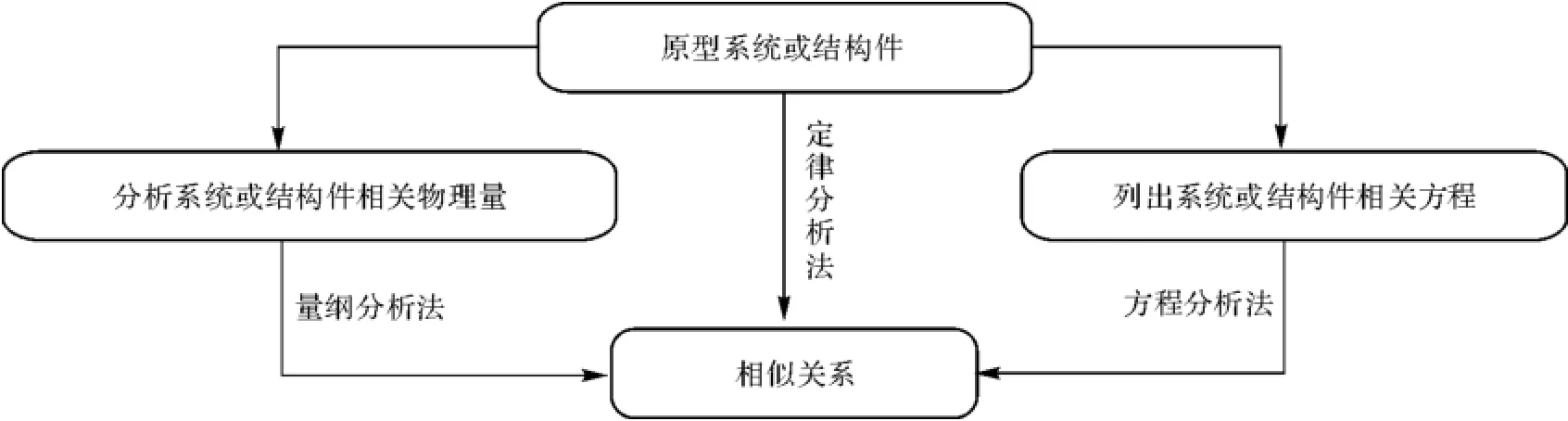
图5 相似关系确定流程Fig.5 Flow chart of determination of scaling laws
2.3.1 基于量纲分析法建立相似关系
量纲分析法是对有关过程物理量的量纲进行分析,得到较少数量的无量纲参数间关系,其理论依据是白金汉π定理。其具体应用步骤如下。
【step 1】 列出与研究问题相关的全部物理量(包括有量纲量、无量纲量和量纲常数),计算其总数量n。
【step 2】 列出n个物理量中每一个物理量的基本量纲,求出基本量纲总数量m和基本物理量数量j,选出j个基本物理量。
根据白金汉π定理,在选取基本物理量的过程中,基本物理量的数量要求在满足涵盖基本量纲的同时,保证数量最少。基本物理量选择准则如下。
[基本物理量选择准则之一] 基本物理量必须包括所有基本量纲。
[基本物理量选择准则之二] 基本物理量的量纲必须彼此独立,自身不能形成一个无量纲组合。
[基本物理量选择准则之三] 不能选择所研究的非独立变量作为基本物理量。
[基本物理量选择准则之四] 不能选择无量纲量作为基本物理量。
[基本物理量选择准则之五] 尽量选择量纲常数而不是量纲参数作为基本物理量。
[基本物理量选择准则之六] 尽量选择简单参数而不是复杂参数作为基本物理量。
[基本物理量选择准则之七] 尽量选择常见参数作为基本物理量。
【step 3】 根据白金汉π定理计算π的个数i。

式中,n为全部物理量总数;j为基本物理量数。
【step 4】 将i个物理量分别与j个基本物理量构造i个无量纲量π并作必要处理。在处理过程中,应根据相似准数性质进行。
[相似准数性质之一] 相似准数的n次方仍是相似准数。
[相似准数性质之二] 相似准数的乘积仍是相似准数。
[相似准数性质之三] 相似准数乘以无量纲数仍是相似准数。
[相似准数性质之四] 相似准数的和与差仍是相似准数。
[相似准数性质之五] 相似准数中任一物理量用其差值形式代替仍是相似准数。
【step 5】 写出最终函数关系式并进行检查。
2.3.2 基于方程分析法建立相似关系
量纲分析法虽然能够得到试验所需的缩比关系式,但存在以下不足。
(1)有可能遗漏表征现象特征的重要物理量,或者选入一些次要的,或者对现象来说关系不大的物理量,甚至是错误的物理量。
(2)难以区别量纲相同,但物理意义不同的物理量(例如,压力、应力、弹性模量等的量纲均为[M-L-T],但意义却不同),从而无法显示现象的内部结构,寻找其中规律。
(3)难以控制量纲为零的物理量(如摩擦系数,阻尼比等),尽管这些物理量具有自身的物理意义,但置入与否并不影响其余相似准则的形成,很容易将其忽略,给分析模型的制作造成困难,限制了缩比关系式的应用范围。
方程分析法以相似现象的物理方程相同为依据,由分析描述现象的方程得出相似准数,其应用步骤如下。
【step 1】 写出描述物理现象的基本方程和单值条件。
【step 2】 写出方程中各参数的相似常数。
【step 3】 进行相似转换(根据相似现象中各物理量保持相同比例),将描述原型各方程中的物理量用模型中的量和相似常数进行表示。
【step 4】 将原型的基本方程与模型的基本方程对照,方程各对应项依次相等,得出各项系数(即相似常数)间的关系式。
【step 5】 对各项系数进行整理,得出各个参数相似常数间的关系——保证完全相似的相似关系。
3 弹性薄板的动力学相似理论
在工程实践中,对于大型机械系统,直接采用真实结构系统进行试验存在很大局限性,例如,试验成本高、影响因素多、试验难度大,甚至难以实现,等等,需要通过缩尺动力学相似模型开展试验研究;同时,有些微尺寸系统也很复杂,无法直接采用原型完成试验研究,需通过放大尺寸相似模型开展试验研究。动力学相似理论研究,其核心价值在于通过相似试验模型(缩尺模型或放尺模型)研究复杂系统的动力学特性及其故障产生机理。
无论是采用缩尺相似模型或是大尺相似模型展开动力学相似研究,其立足点有二,一是可以合理调整结构、材料和工艺,大幅降低试验成本,如对于大型高速旋转系统,通过动力学相似,不仅可以减小模型几何尺寸,而且还可以降低试验模型的临界转速;二是可以人为控制主要影响因素,剔除次要影响因素,简化试验模型结构,降低试验难度,缩短试验周期。这其中,所设计试验模型与原型的动力学相似是首要条件。
所谓复杂系统模型试验的动力学相似设计,是指为了达到让试验模型与真实结构(原型系统)的动力学固有特性、动力学响应行为、甚至包括典型故障特征等在一定范围内一致或成固定比例关系,而建立起模型与原型的结构参数(几何尺寸、结构形状)、材料参数(密度、弹性模量、泊松比、刚度和阻尼)、载荷条件(激励大小、方向和位置)、连接方式(套齿连接、螺栓连接或焊接,等等)、支承条件(刚度、阻尼)和边界条件(转速、结构耦合作用形式)成比例映射关系的方法。
复杂转子系统模型试验涉及系统动力学特性问题,不仅受到每个结构件动力学特性的影响,更受到系统结构件之间结构耦合非线性特征(如叶片-轮盘结构特征、轴承-支承结构特征、套齿联轴器结构特征、气体封严和润滑密封,等等)和动力学非线性特性耦合(如各结构件间的连接方式,各结构件间的能量传递,等等)的影响。故此,在建立复杂转子系统的动力学相似关系时,考虑结构件间的耦合作用及各结构件畸变对于整个模型结构系统的动力学特性的影响,具有关键意义。但是,由于复杂系统的结构形式和工作承载情况非常复杂,试验模型满足动力学相似关系,存在一系列尚待解决的科学问题和工程问题。
目前,复杂系统动力学相似模型的研究尚处于初创阶段,笔者试图先从结构件入手开展研究,然后考虑系统耦合因素等问题,逐次上升到系统级,最终建构复杂系统的动力学相似设计方案。为简化说明机械结构动力学相似设计的基本理论与方法,本文以大型高速旋转机械系统中常见的弹性薄板构件为例,加以阐述。
3.1 弹性薄板的基本理论
在弹性力学中,两个平行面与垂直于它们的柱面或棱面所围成的物体,当其高度小于底面尺寸时称为板(plate),两平行面称为板面(surface),柱面或棱柱面称为板边(flank),两平行平面之间的距离称为板厚(thickness),平分板厚的平面称为中面(middle surface)(见图6)。
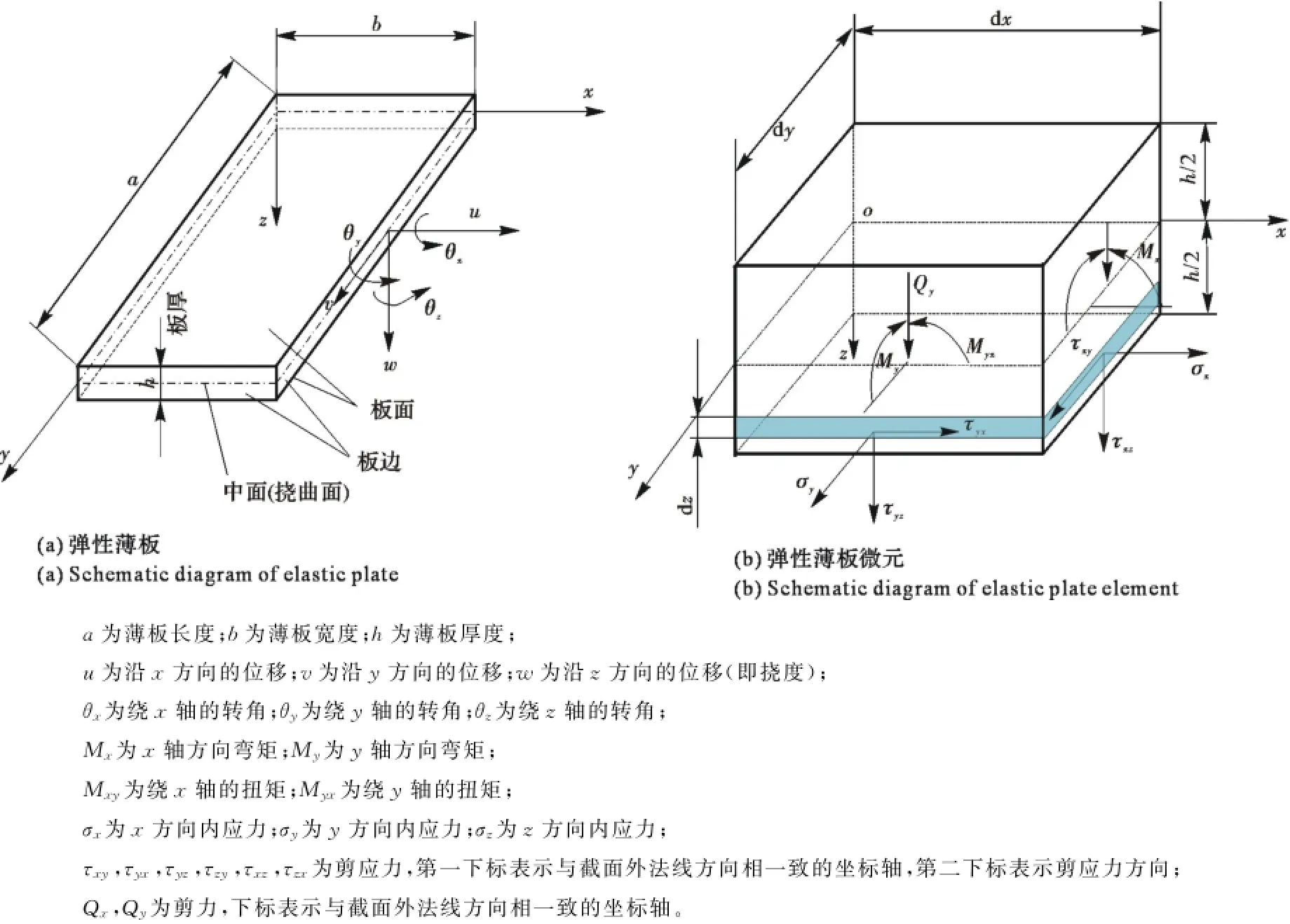
图6 弹性薄板及单元示意Fig.6 Schematic diagram of elastic plate and element
图6 中,当全部载荷作用于中面时属于平面应力问题;当全部载荷垂直于中面时主要发生弯曲变形,中面由弯曲变为曲面,称为挠曲面(deflection surface)[74]。
【定义13 特征尺寸(eigen size)】 表征物体几何特征的尺寸。
【定义14 最小特征尺寸(minimum teature size)】 长度值最小的特征尺寸。
【定义15 薄板(thin plate)】 当板厚与板面内的最小特征尺寸之比
【定义16 弹性薄板(elastic thin plate)】 变形行为符合胡克定律的薄板。
3.1.1 基本方程
薄板小挠度弯曲理论是基于以下3个计算假定的[75]。
【假定1】 垂直于中面方向的正应变εz极其微小,可以忽略不计。
【推论1】 根据“假定1”,在中面的任一法线上,薄板的全厚度内,所有点具有相同的位移。
【假定2】 τxz,τyz和σz远小于σx,σy,τxy。其所引起的应变可以忽略不计。
【推论2】 根据“假定2”,中面的法线在薄板弯曲时保持不伸缩,成为弹性曲面的法线。
【假定3】 薄板中面内的各点没有平行于中面的位移。
【推论3】 根据“假定3”,中面内的任何一部分虽然弯曲成为曲面的一部分,但在xy面内的投影保持不变。
(1)位移函数 根据“假定1”,可以得到如下关系。

式中,εz为z方向应变。
挠曲面行为可以表示为如下形式。

根据“假定2”,薄板弯曲后,板的法线与弹性曲面在x方向和y方向的切线都保持互相垂直,没有剪应变,故而

式中,γyz为yz面内的剪应变;γxz为xz面内的剪应变。
由式(24)可以推知

式(25)对z积分,当注意到w与z无关时,可以得到如下关系。

式中,f1(x,y)和f2(x,y)为任意函数。
根据“假定3”,可以得到如下关系。

由式(26a)和式(26b)可知,当f1(x,y)=f2(x,y)=0,则板上任意一点沿x,y,z等3个方向的位移

可见,当薄板小挠度弯曲问题被简化为中面弯曲问题时,只要中面挠度w确定,任何点的位移都可确定。
(2)几何方程 根据上述分析,由式(28),薄板的几何方程可以表示为如下形式。

式中,εx为x方向应变;εy为y方向应变;γxy为x y面剪应变。
(3)本构方程 根据“假定2”,若在本构方程中不考虑τxz,τyz和σz,则薄板弯曲问题的本构方程(应力与应变的关系)如下。
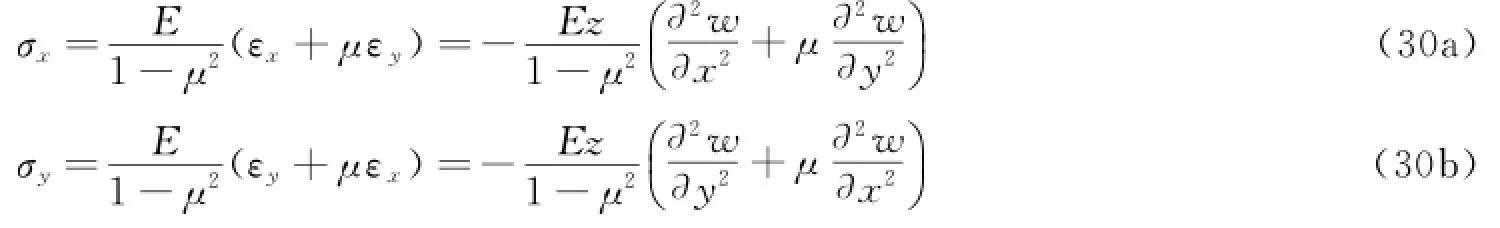

式中,μ为泊松比;E为弹性模量;G为剪切模量。
(4)平衡方程 虽然在本构方程分析中不考虑τxz,τyz和σz的影响,但它们是构建平衡方程所必需的。对薄板微元体进行受力分析,由于各个方向受力平衡,可以得到薄板的平衡方程[76]。

式中,Fx为x方向上的外力;Fy为y方向上的外力;Fz为z方向上的外力。
在x轴方向的弯矩Mx,绕x轴的扭矩Mxy,剪力Qx可以表述为如下形式。
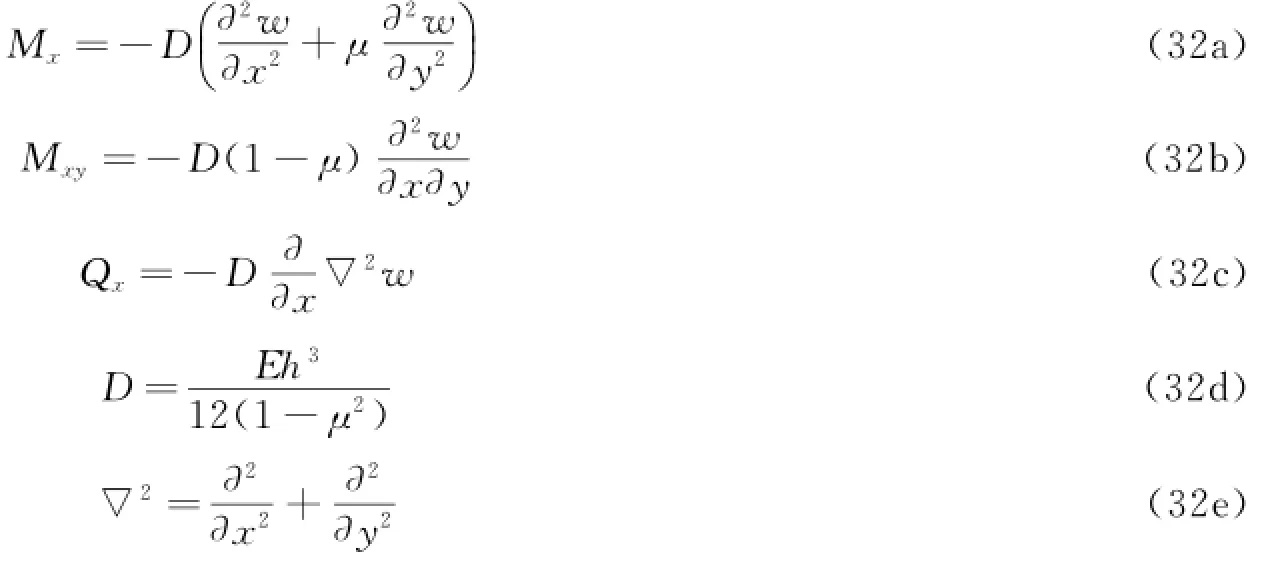
式中,D为板的弯曲刚度;∇2为Laplace算子。
在y轴方向的弯矩My,绕y轴的扭矩Myx,剪力Qy可以表述为如下形式。

同理,可以得出薄板各个截面上的应力分量与弯矩、扭矩、剪力、载荷的关系。
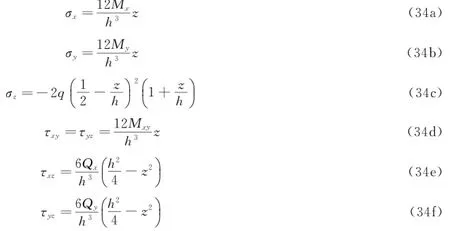
式中,q为匀布载荷大小。
(5)边界条件 薄板的内力、挠度、应力等变量应结合边界条件进行求解,不同的边界条件需满足不同的关系。
对于固支边,沿约束边缘的挠度与转角均为0,其边界条件如下。

对于简支边,沿约束边缘的挠度及转矩均为0,其边界条件如下。

对于自由边,边界没有限制挠度和转角的约束,其边界条件如下。
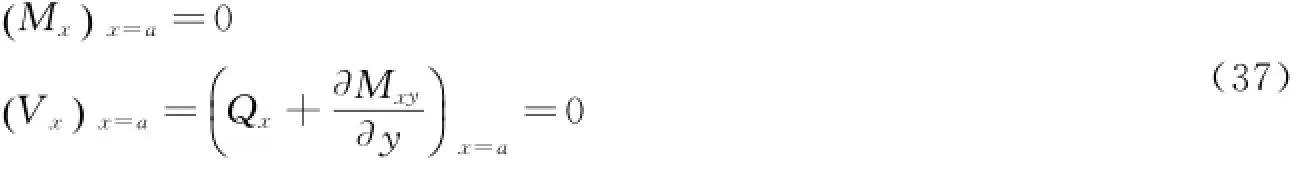
式中,Vx为当x=a时,边缘上等效横向剪力。
3.1.2 矩形薄板的自由振动方程
设薄板在振动过程中任何一瞬时时刻t的挠度为w=w(x,y,t)(不从平面位置量起,而从平衡位置量起),将式(34)代入式(31),则薄板每单位面积在该瞬时所受的弹性力大小为D∇4w,而可以将惯性力写成如下形式。

式中,qi为单位面积惯性力为薄板单位面积质量。
将弹性力与其惯性力qi相平衡,可得其自由振动方程。3.2 相似关系

按照量纲分析法作业步骤,建立弹性薄板动力学相似关系。
【step 1】 列出与所要研究问题相关的全部物理量,计算其总量n。
影响弹性薄板结构动态特性的主要因素来源见表1。
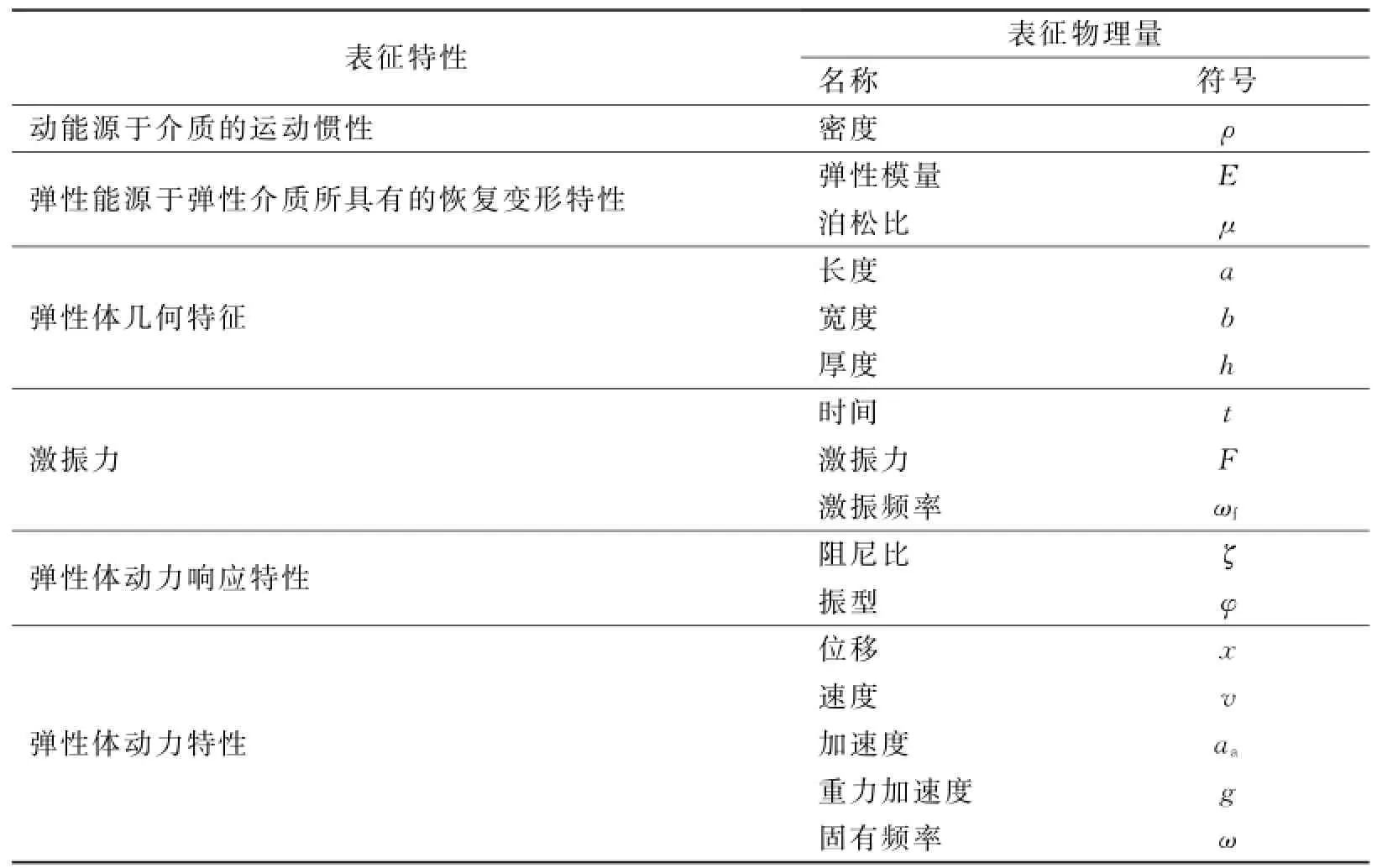
表1 影响弹性薄板结构动态特性的因素及其表征Tab.1 Parameters affecting the dynamic characteristics of thin plate
由表1可知,影响弹性薄板结构动态特性的相关物理量总数n=16。
【step 2】 列出n个物理量中每一个物理量的基本量纲。
采用[M][L][T]量纲系统([M]为质量量纲,[L]为长度量纲,[T]为时间量纲)作为基本量纲,可得弹性薄板的量纲关系(见表2)。

表2 量纲关系Tab.2 Dimension relationship
设α1~α16分别代表各相关物理量的幂次,可得弹性薄板的量纲关系(见表3)。
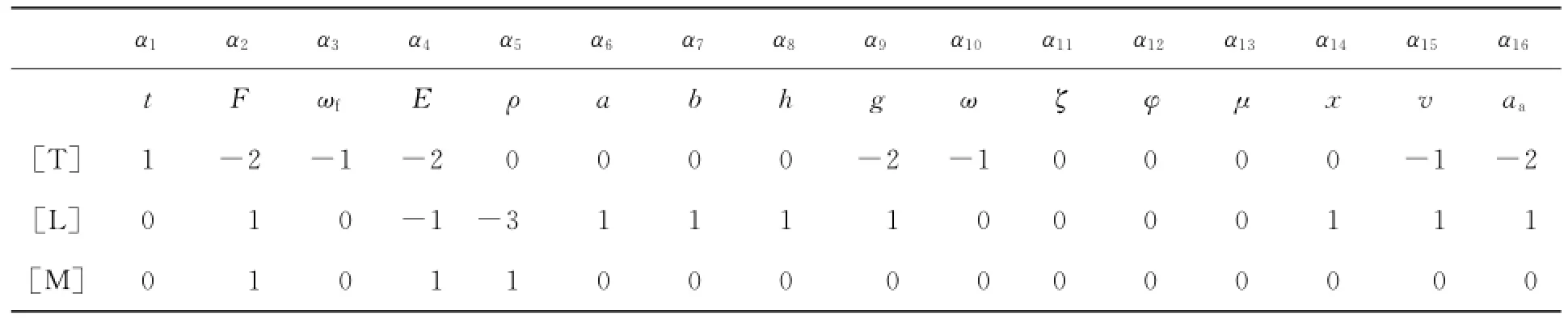
表3 变换后的量纲关系表Tab.3 Dimension relationship after transformation
【step 3】 根据白金汉π定理计算π的个数i。
物理参数的数量为16,采用[M][L][T]量纲系统,基本量纲数j为3,则独立π数的个数

【step 4】 将i个物理量分别与j个基本物理量构造i个无量纲量π,并作必要处理。
弹性薄板受谐波激振力作用产生振动,各主要物理参数之间的关系一般形式如下[76]。
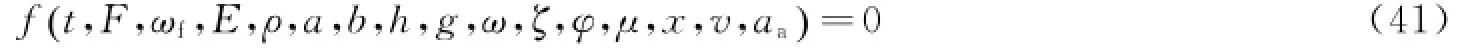
对于弹性薄板,将π项理解为16个物理参数的函数关系。
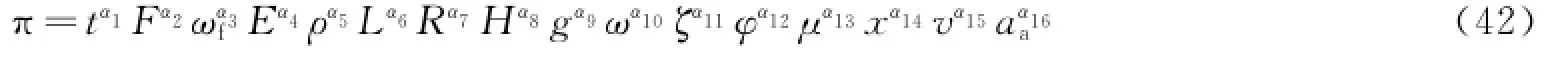
式(42)为弹性薄板的相似准数一般形式。
根据量纲分析方法,可得3个线性齐次代数方程。
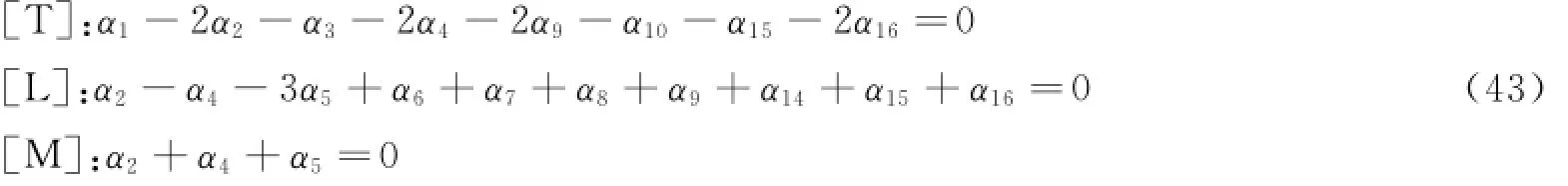
求解式(43),可得
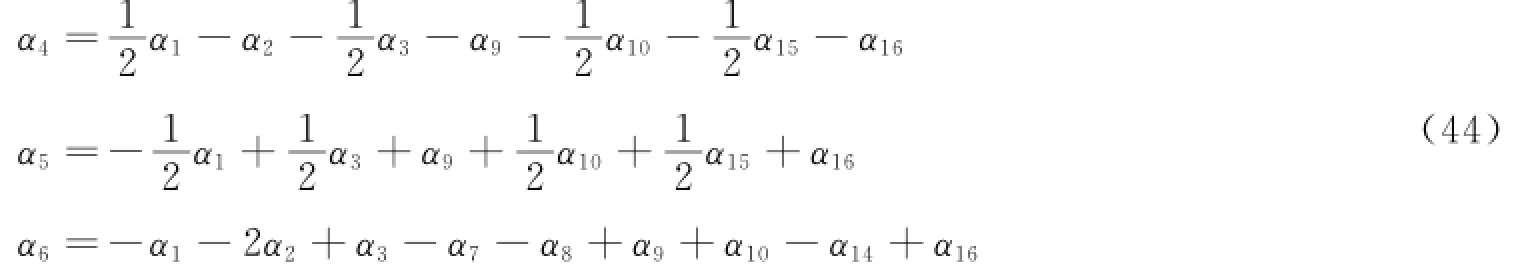
由白金汉π定理出发,将式(44)改写为如下形式。

根据式(45),对于16个幂次指数αi,有如下形式。

根据式(46),可得各物理参数的指数π矩阵(见表4)。
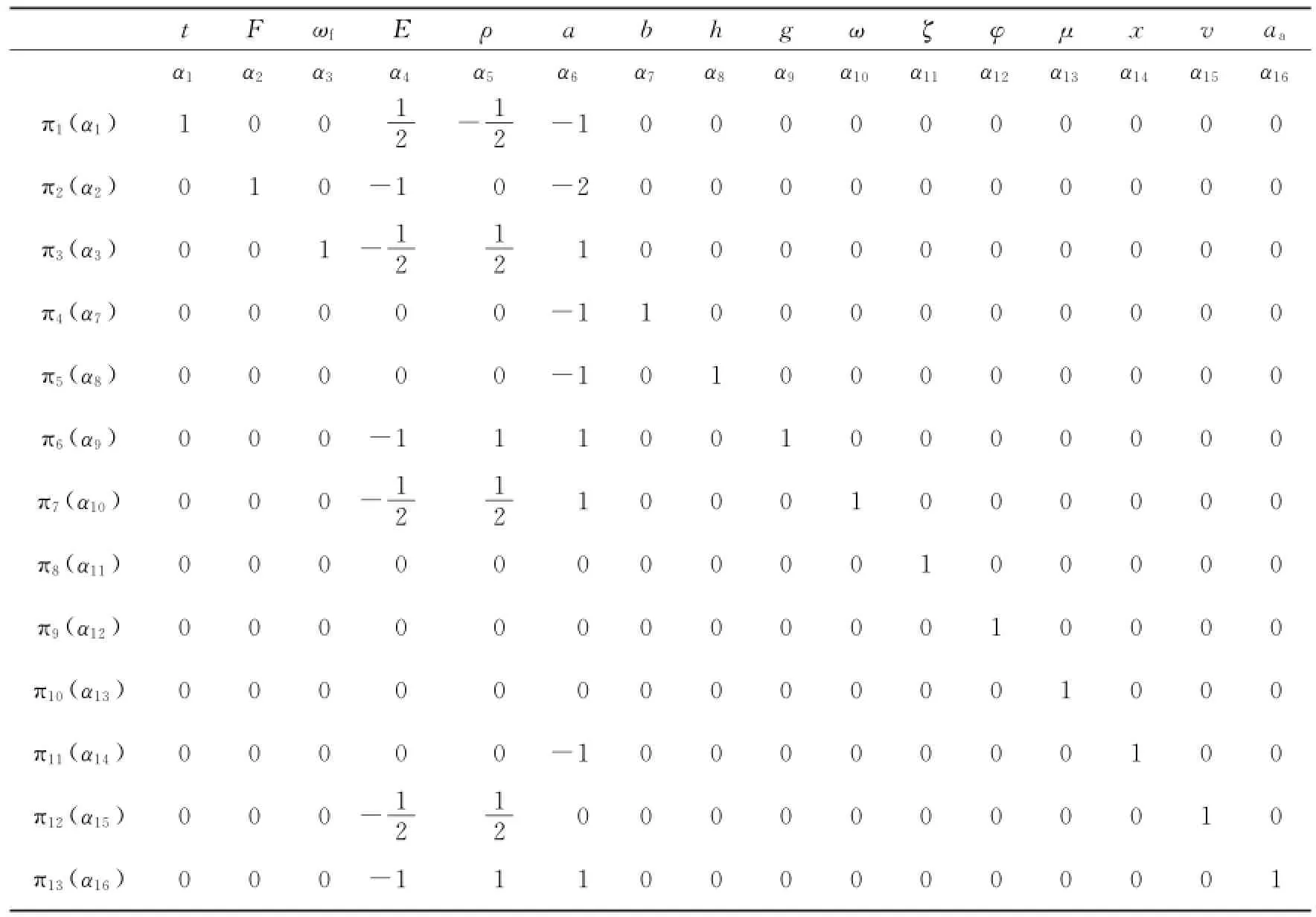
表4 指数π矩阵Tab.4 Matrix ofπ
【step 5】 写出最终函数关系式并进行检查。
对表4进行整理,可得如下关系。

在弹性薄板相似模型设计中,相似模型和原型对应的物理量应成比例,故而有如下形式。
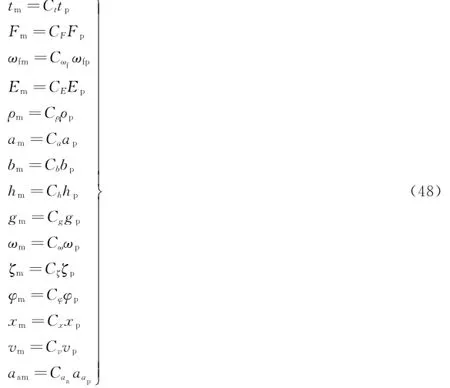
式中,tm模型时间;tp为原型时间;Ct为原型与模型时间相似比;Fm为模型载荷;Fp为原型载荷;CF为原型与模型载荷相似比;ωfm为模型激振频率;ωfp为原型激振频率;Cωf为原型与模型激振频率相似比;Em为模型弹性模量;Ep为原型弹性模量;CE为原型与模型弹性模量相似比;ρm为模型密度;ρp为原型密度;Cρ为原型与模型密度相似比;am为原型长度;ap为模型长度;Ca为原型与模型长度相似比;bm为原型宽度;bp为模型宽度;Cb为原型与模型宽度相似比;hm为原型厚度;hp为模型厚度;Ch为原型与模型厚度相似比;gm为模型重力加速度;gp为原型重力加速度;Cg为原型与模型重力加速度相似比;ωm为模型固有频率;ωp为原型固有频率;Cω为原型与模型固有频率相似比;ζm为模型阻尼比;ζp为原型阻尼比;Cζ为原型与模型阻尼比相似比;φm为模型振型;φp为原型振型;Cφ为原型与模型振型相似比;xm为模型位移;xp为原型位移;Cx为原型与模型位移相似比;vm为模型速度;vp为原型速度;Cv为原型与模型速度相似比;aam为模型加速度;aap为原型加速度;Caa为原型与模型加速度相似比。
将式(48)代入式(47),经简化可得弹性薄板相似模型应满足的相似条件。
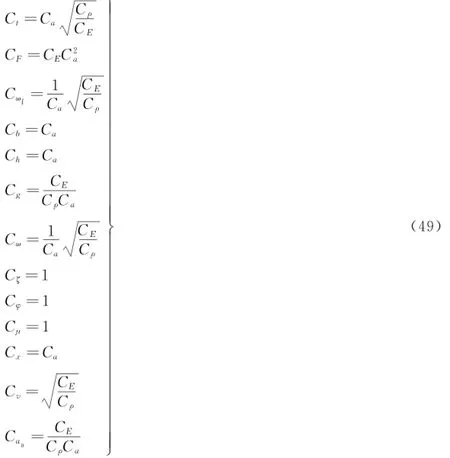
式(49)中的13个相似条件包含16个相似常数,故有3个相似常数需要预先确定。
【先定规则1】 在实际设计中,模型材料要先行选定,故而CE和Cρ可以预先确定。
【先定规则2】 因为模型为缩尺寸比例模型,故而Ca可以根据要求预先确定。
根据式(49),可以得到弹性薄板动力相似关系的相关规则。
【相似规则1】 在缩比模型的设计中,如果长、宽、厚等3个几何参数以相同比例数变化,则Ca,Cb和Ch可用同一个量纲表示。
【相似规则2】 相似模型和原型本征方程相同,具有相同的模态主振型,并且对于几何相似的缩比模型和原型,其固有频率与几何缩比成反比。
【相似规则3】 当缩比模型和原型为不同材料时,其固有频率正比于弹性模量和密度的缩比比值的平方根。
3.3 弹性薄板模态调节方法
3.3.1 带集中质量块的薄板振动理论
根据薄板小挠度理论假定,均匀质量薄板受迫振动微分方程可以表示为如下形式[77-81]。
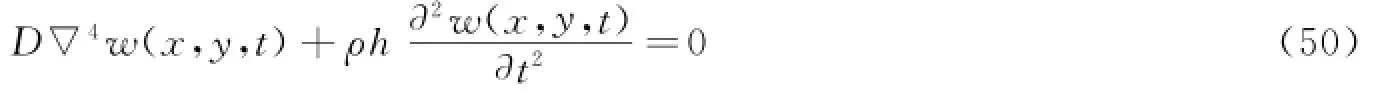
式中,w(x,y,t)为任意一点瞬时t的挠度;(x,y)为薄板任意一点的坐标。
当薄板带有集中质量块(concentrate mass)时,由式(50)可得其振动微分方程。
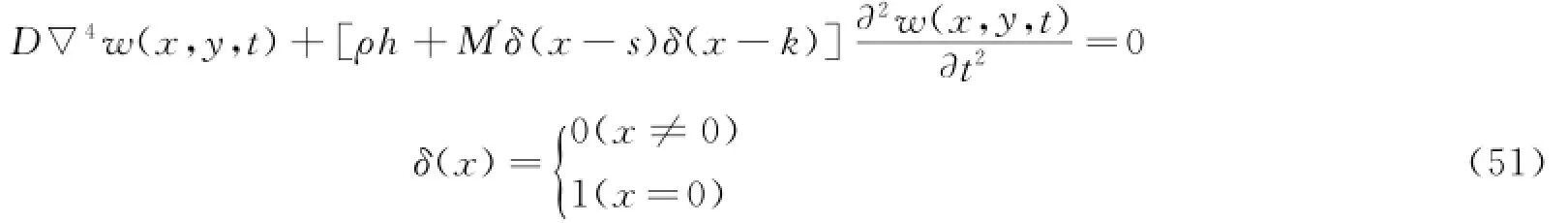
式中,M′为集中质量块的质量;(s,k)为集中质量块在xy平面上的位置。
若不考虑剪切变形的影响,则其最大应变能
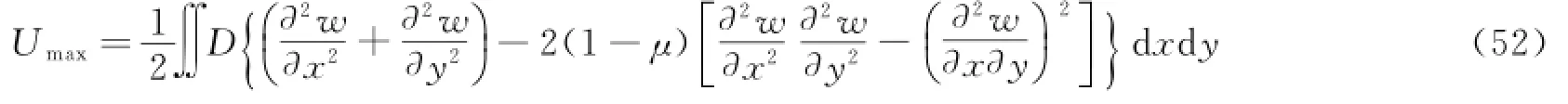
若不考虑转动惯量的影响,则其最大动能
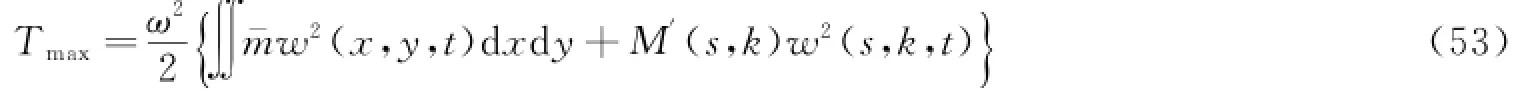
综合式(46)~式(49),可以得到带单一质量块薄板的固有频率。
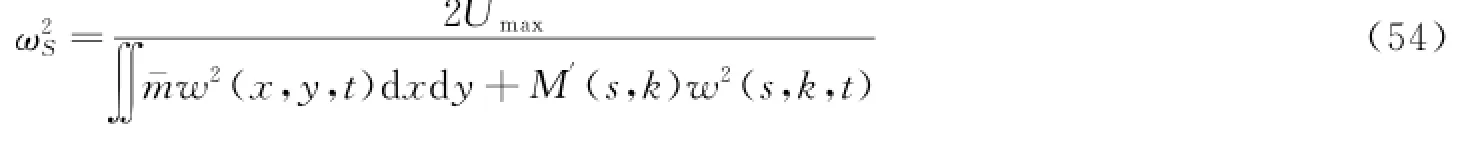
式中,ωS为带单一质量块薄板的固有频率。
当考虑质量块分布面积时,其自由振动微分方程可表述为如下形式。

式中,mρ为质量块单位面积的质量;A为质量块质量的分布面积。
由式(50)和式(51),可得考虑质量块分布时的薄板固有频率。

根据式(56),集中质量块的质量、在薄板上的位置、质量块数量和分布面积,对薄板振动频率和振型均有影响。
在不同的边界条件下,均匀薄板各点位移的表达式w(x,y,t)也不同,若知道任意边界条件的均匀薄板的模态函数,就可求得相应边界条件下带附加集中质量薄板的固有频率及对应振型。
3.3.2 集中质量块对振动模态的影响
由文献[82]的研究得知,相对于其他影响因素,质量块在薄板上的位置和质量(相同体积下表现为材料)对薄板振动特性的影响更为显著,故本文考虑这两个影响因素。
为便于说明,设薄板的基本结构参数和材料参数见表5。采用solid95单元类型进行有限元建模,边界条件为一边为固支边,其余三边为自由边。

表5 薄板材料参数表Tab.5 Material parameters of thin plate
(1)质量块位置对薄板特性的影响 为了研究质量块在薄板上的不同位置对频率的影响规律,质量块的位置采用比值坐标形式表示。
设质量块的长、宽、高相等,即a′=b′=h′=6 mm。质量块的材质与薄板相同。质量块的位置比值坐标分别为(1,1),(1,2),…,(5,5),共25种情况(见图7)。
考虑到对称性,分别计算质量块比值坐标为(x,y)(x=1,2,…,5;y=1,2,3)时的各阶固有频率(见图8)。由图8出发,可以得到以下判读。
【判读1】 在图8(a)中,固有频率变化折线随着集中质量块位置沿x轴变化呈现非线性变化,影响逐步增大;沿y轴的变化不明显,变化幅度更为平均,更接近于线性变化(不考虑边界点)。
【判读2】 在图8(b)中,固有频率变化折线呈现出周期性变化;随着集中质量块位置沿x轴移动呈下降趋势,沿y轴移动呈上升趋势。
【判读3】 在图8(c)中,固有频率变化折线在集中质量块位置在x=2和x=3时的影响较为显著。

图7 薄板的比值坐标系Fig.7 Ratio coordinate chart of thin plate
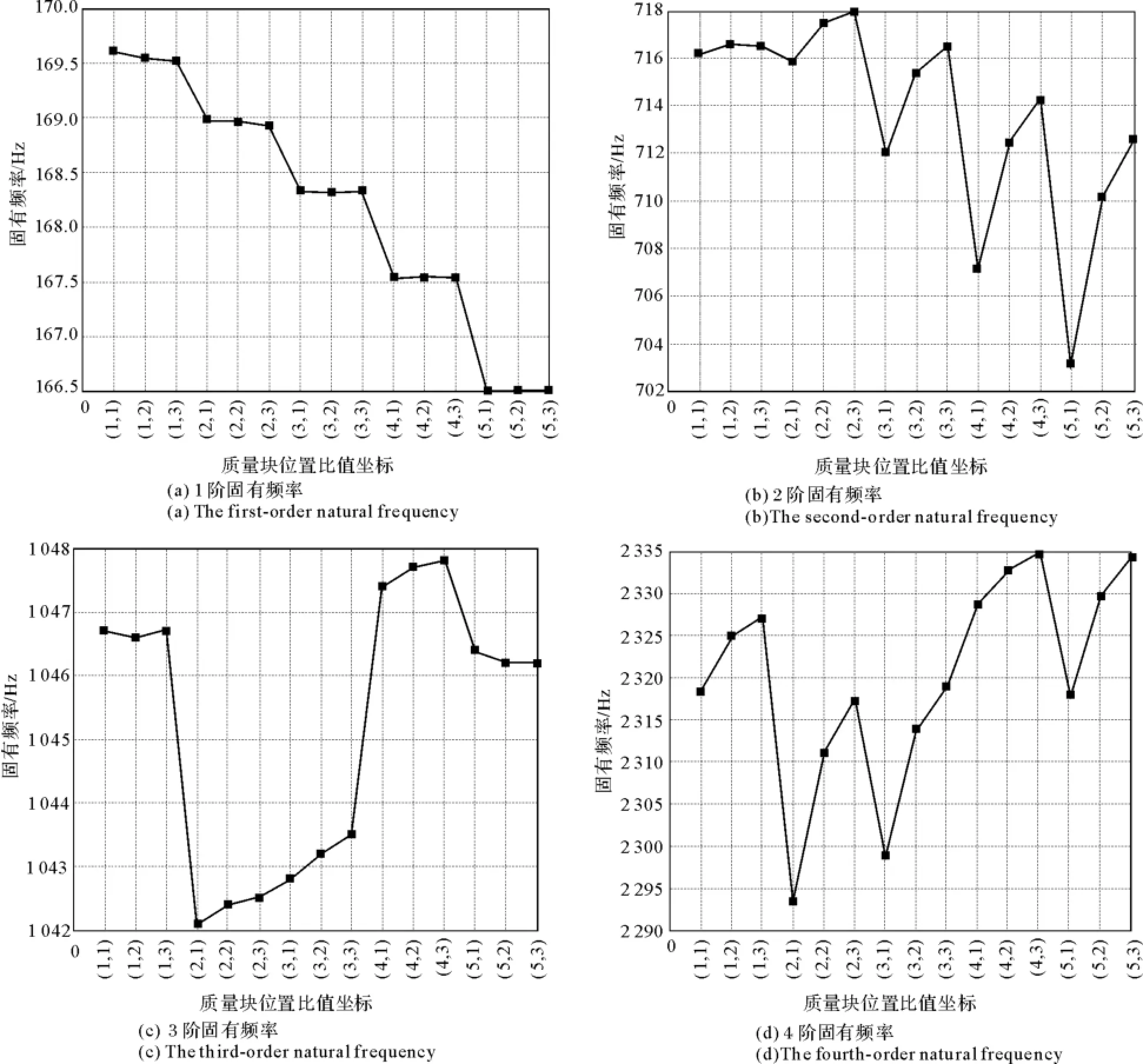
图8 集中质量块位置对固有频率的影响Fig.8 Effect of the position of concentrated mass on natural frequency
【判读4】 在图8(d)中,固有频率变化折线在集中质量块位置在x=2和x=3处波动较大。
由此,可以得到如下结论。
【结论1】 附加集中质量块后,在绝大部分位置上薄板的固有频率降低,仅有个别位置上薄板的固有频率略有升高,起到了增强刚度的作用。
【结论2】 集中质量块的位置与薄板某一阶振型中的节线位置距离越远,对薄板的该阶固有频率影响越大,即敏感性越强。
这也可以由未加质量块时悬臂薄板的前四阶振型(见图9)得知。
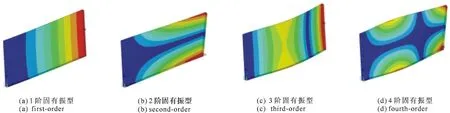
图9 薄板的前4阶振型Fig.9 Plate vibration in the first four orders
(2)质量块材料对弹性薄板特性的影响 当将质量块置于比值坐标(3,1)时,对薄板的前4阶固有频率的影响均较为显著,因此,在分析质量块材料对弹性薄板固有特性影响时,质量块的坐标位置选为(3,1),质量块几何尺寸为a′=b′=h′=6 mm,弹性薄板材料为钛合金,质量块选普通钢、铝镁合金和钛合金等3种材料(材料参数见表6)。

表6 质量块材料参数Tab.6 Three material parameters of concentrated mass
图10为质量块材料与弹性薄板材料不同时前十阶固有频率差值。横坐标为不同阶次,纵坐标为频率差值。

图10 质量块材料对固有频率的影响Fig.10 The effect of mass material on natural frequency
由图9出发,可以得到以下判读。
【判读5】 当质量块材料为比钛合金密度大的普通钢时,质量块使弹性薄板的固有频率增大,各阶固有频率的增大量不是线性的,这与质量块所在弹性薄板上的位置、各阶固有频率对应的振型以及边界条件均有关系;
【判读6】 当质量块材料为比钛合金密度小的铝合金时,质量块使弹性薄板的固有频率降低,其对各阶固有频率的影响规律同前者。
综合质量块在弹性薄板上的位置以及材料对薄板频率的影响规律,可得出如下结论。
【结论3】 用集中质量块可调整结构的固有频率,且应将质量块置于振型中心,同时质量块的材料对其也有加大影响。
【结论4】 在调整不同阶次下的固有频率时,由于有时振动会出现多个峰值的现象,只将质量块放置于一个波峰处时,对固有频率的改变量小于将质量块分散到所有峰值点时的固有频率改变量。这一点对于高阶模态的调整更有效。
因此,在进行弹性薄板的动力学相似试验模型设计时,可依据以上结论,根据试验内容可在保证模态振型与原型一致的条件下,有目的的进行固有频率调节;也可根据需要调整振型,实现人为控制相似模型试验的主要影响因素,使试验更有针对性。
3.4 弹性薄板类结构动力学相似设计方法实例
由弹性薄板集中质量的分析可知,通过调整薄板表面集中质量的施加方式可以对薄板固有频率进行调节,通常由于测试条件的限制,需要在模型设计时降低相应的固有频率,并能够避免共振频率,通过相似设计方法与对质量块影响的分析,采用弹性薄板实例对设计方法进行论述。
3.4.1 降低固有频率的相似设计方法
在工程应用中,薄板类结构件极为常见。设计时,因需满足不同的设计要求,需对原有结构进行适当的相似设计。根据薄板相似设计方法,提出弹性薄板类结构件(见图11)相似设计设计实例。
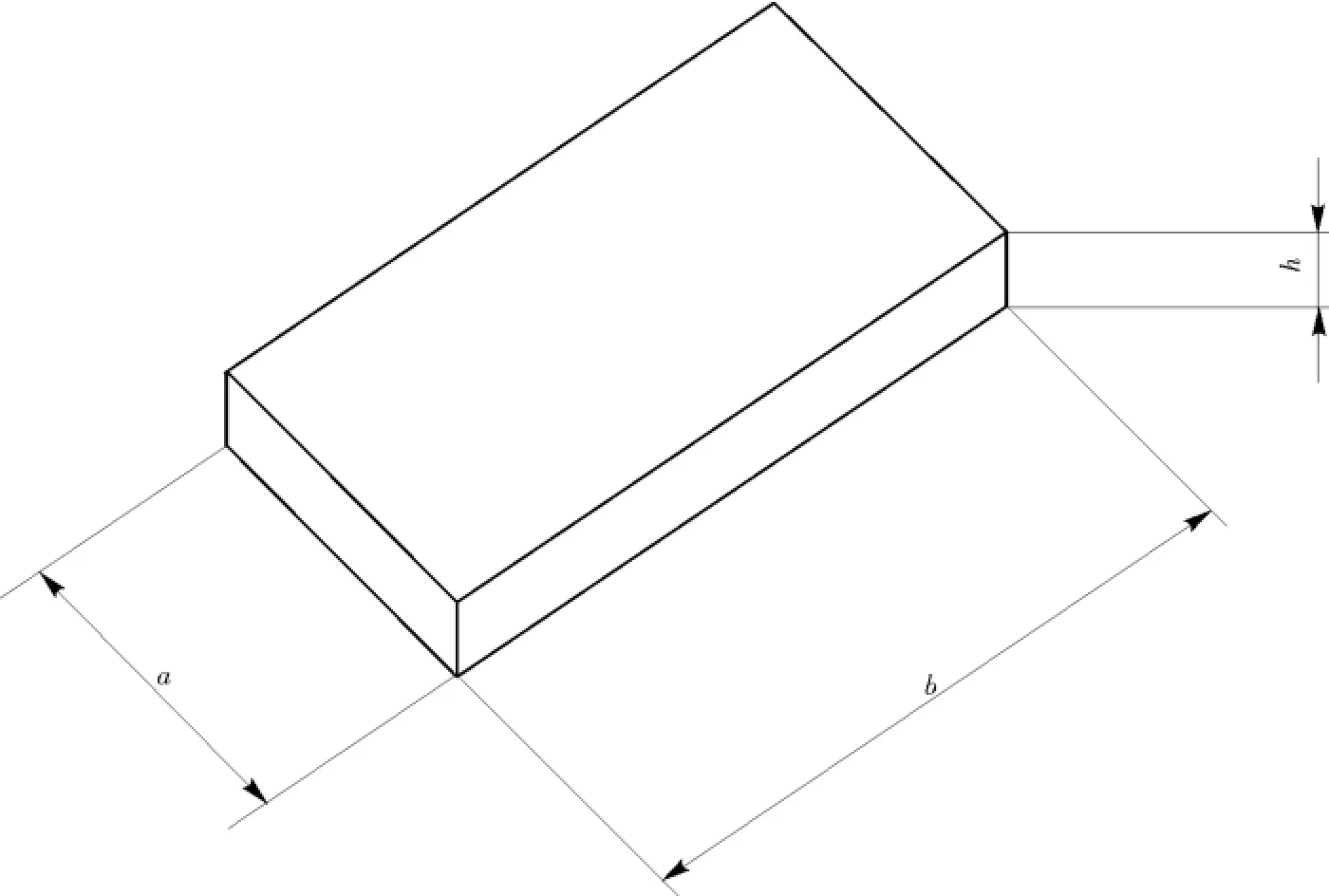
图11 薄板类结构件Fig.11 Schematic diagram of thin plate member
原型构件的材料和几何参数见表7。

表7 原型构件的相关参数Tab.7 Parameters of prototype structure
为了实现对其固有特性的预测,可将边界条件简化为四边固支。利用有限元分析软件,得到其各阶固有频率及阵型图(见表8)

表8 各阶固有频率及振型Tab.8 Natural frequencies and vibration models of each order
【任务要求】 降低上述结构件的各阶固有频率,使之为原固有频率的50%。
【方案1 采用同一种材料】 当采用同一种材料时,构件的材料参数不发生变化,即材料参数的相似缩比系数为1,只考虑几何参数的影响。
根据薄板相似缩比关系

可知,在完全几何相似条件下,固有频率降低为原固有频率的50%,需将几何尺寸扩大为原来的2倍。相似模型m1的相关参数见表9。

表9 相似模型M1的相关参数Tab.9 Parameters of model M1
利用有限元分析软件,得到其各阶固有频率及振型图(见表10)。

表10 相似模型M1的各阶固有频率及振型Tab.10 Natural frequencies and vibration models of model M1
根据以上仿真结果可知,所得到的模型M1的所有固有特性均满足设计要求。
【方案2 采用不同种材料】 当采用材料不同时,构件的材料参数将会发生变化,这导致材料参数的相似缩比系数和几何参数的影响需均衡考虑,故而需要首先确定模型M2的材料参数。假设将原型材料由45 #钢板改为钛合金板,其材料参数见表11。

表11 原型构件的各项参数Tab.11 Parameters of prototype
根据薄板相似缩比关系式

可知,须先计算系数值。
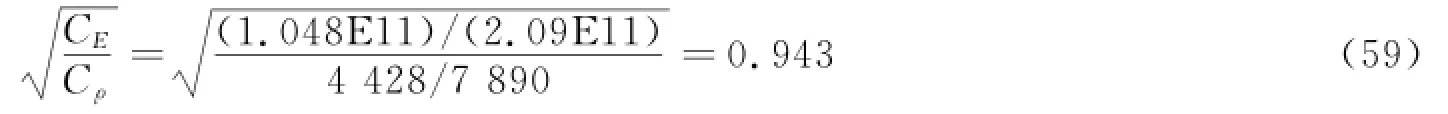
在完全几何相似的条件下,固有频率降为原来的50%,需将几何尺寸扩大为原来的1.886倍,相似模型M2的相关参数见表12。

表12 相似模型M2的相关参数Tab.12 Parameters of model M2
利用有限元分析软件,得到其各阶固有频率及振型图(见表13)。根据仿真结果可知,所得到的模型M2的所有固有特性均满足设计要求。
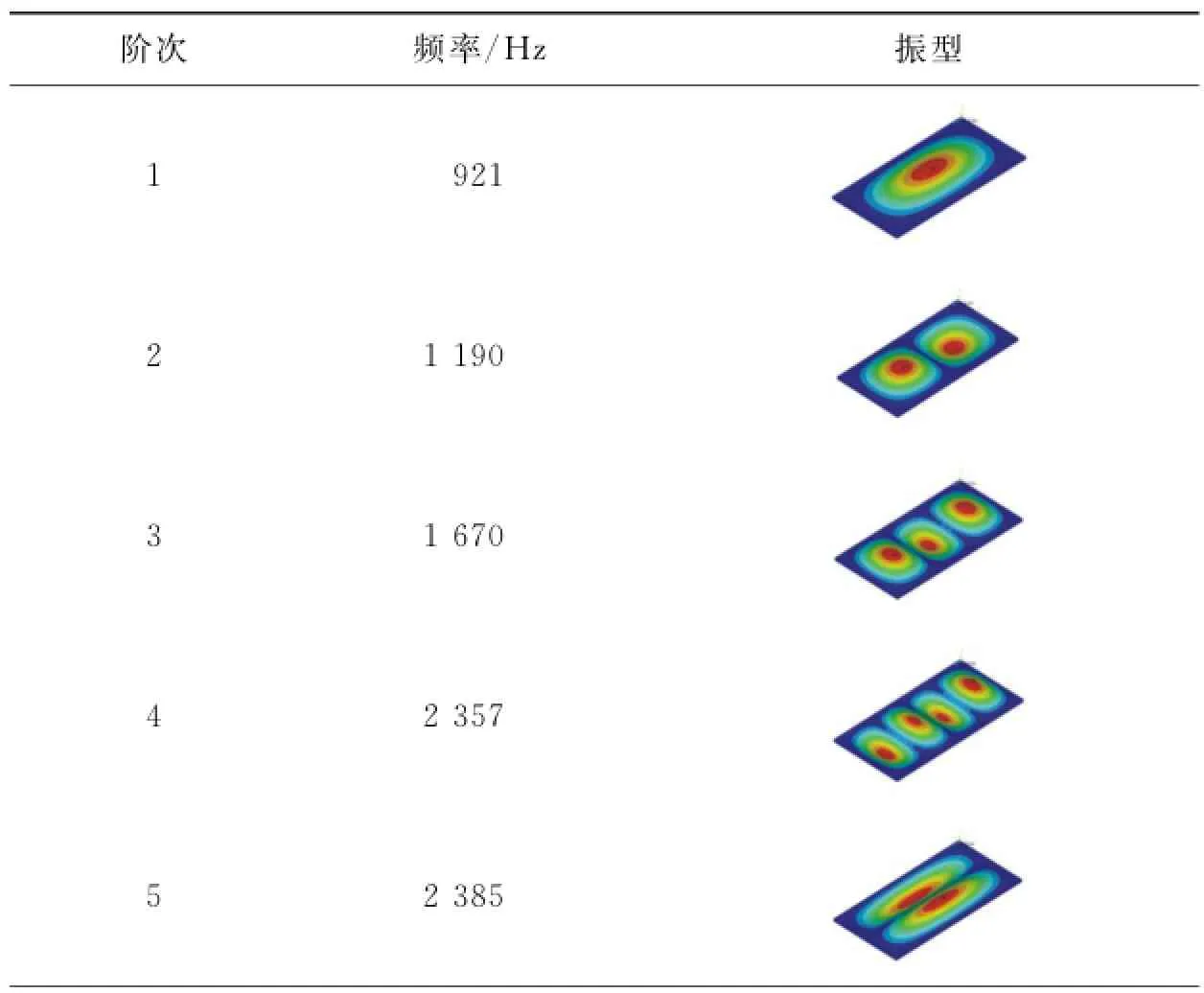
表13 相似模型M2的各阶固有频率及振型Tab.13 Natural frequencies and vibration models of model M2

续表
通过以上实例可以发现,依据动力学相似进行相似设计,在保证振型一致的前提下调整了频率,很好地满足了需要。
3.4.2 基于集中质量块的模型模态调节方法应用验证
在某类叶片振动特性试验中,相似缩尺寸模型的参数见表14,试验激励是频率为3 000 Hz的法向激励[83]。未加质量块前,模型的第2、第3和第4阶固有频率及相应的振型分别见表10和表13。其中,模型的第3阶固有频率为2 889.8 Hz,故在试验过程中,激振力极易引起共振,这是本试验不允许的,故而需采用附加集中质量块调频方法进行调整。

表14 某叶片缩尺模型参数Tab.14 Parameters of one scale-down blade model
由表15和表16可知,附加质量块可调整固有频率,但也可能使模态次序发生较大变化。而本试验要求使第3阶固有频率偏离3 000 Hz的同时,要保证第2阶,第4阶的频率没有较大变化,且不能改变结构的模态次序。基于此,从以上得出的质量块参数对薄板固有频率的影响规律可知,加两个质量块,并且选择质量块的质量与叶片的质量比为0.1。质量块应该尽可能放置于第3阶模态的波峰处,放置于第2、第4阶模态的波节处,质量块分布方法见图12,附加质量块后的固有频率和振型见表15和表16。
由表15知,加质量块后叶片的第3阶固有频率已偏离激振力的频段,比原来降低了约12.21%,而对相邻第2阶和第4阶的固有频率值的影响甚小,分别为0.08%和0.56%,并且各阶模态振型没有被改变,满足试验要求。

表15 加集中质量块前后模型的固有频率Tab.15 Natural frequencies of model before and after adding concentrated mass
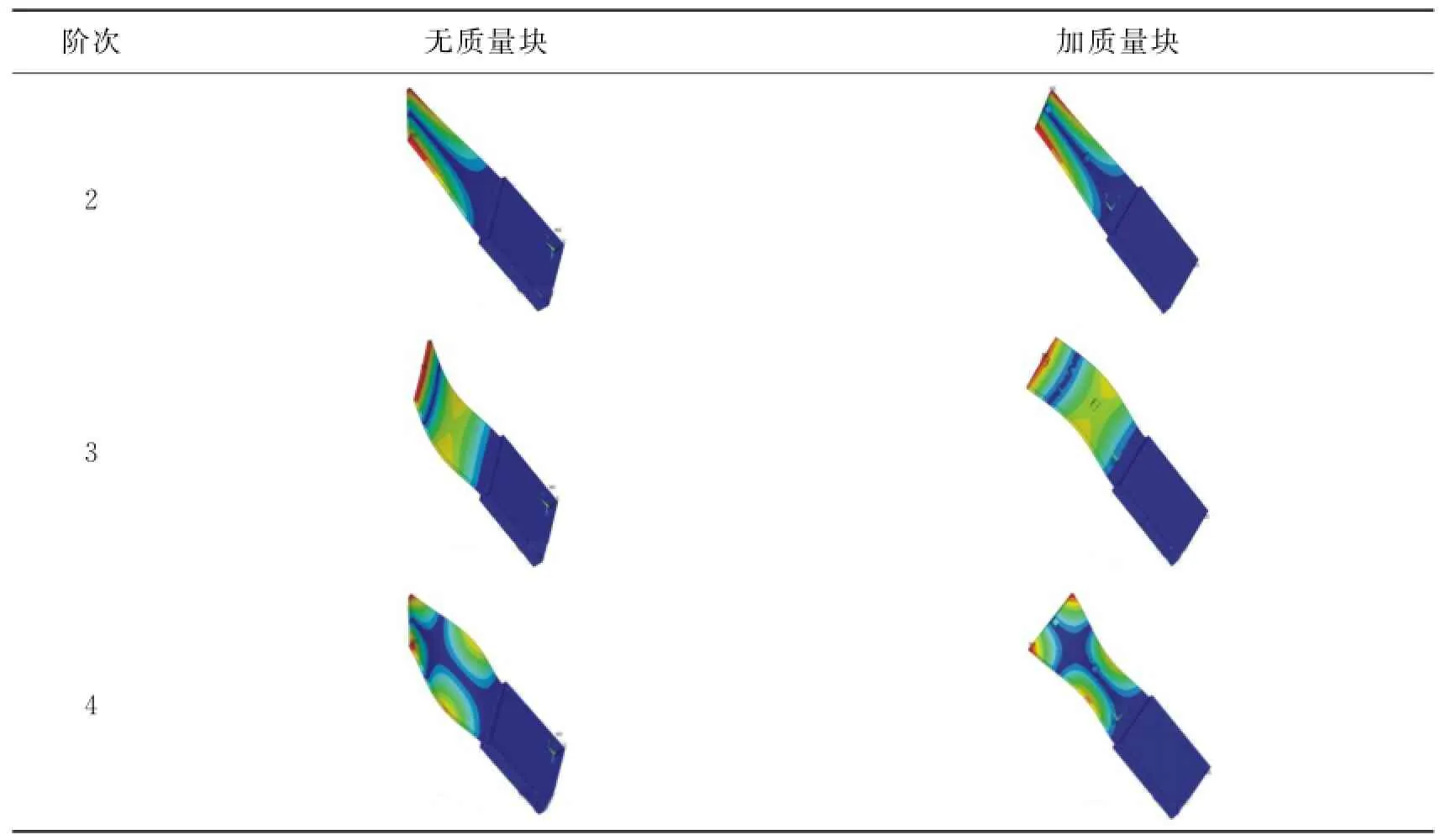
表16 加集中质量块前后模型的振型Tab.16 Vibration model of model before and after adding concentrated mass
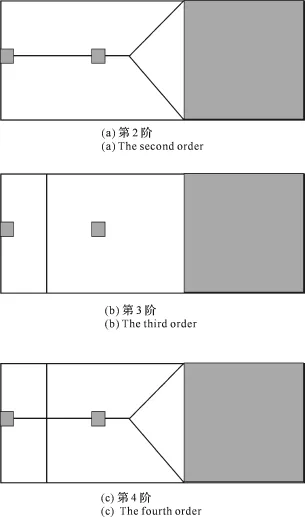
图12 各阶振型简图及质量块位置Fig.12 Diagram of vibration model and the position of mass
4 弹性薄板动力学不完全几何相似设计方法与验证
在动力学相似设计中,往往需要考虑不完全几何相似模型的设计问题。笔者在完全几何相似设计方法的基础上,通过敏感性分析和区间分析,讨论弹性薄板动力学不完全几何相似模型设计方法。
4.1 弹性薄板固有特性敏感性分析
【定义17 不完全几何相似(incomplete geometric similarity)】 结构体几何特征尺寸相似比不相等的相似现象,亦称几何畸变相似(distorted geometric similarity)。
模型和原型对应参数间的相似关系和相似条件,对模型设计有着严格要求,特别是对于变量较多的原型系统,从某种意义上讲,相似关系和相似条件限制了模型的设计。
为了解决上述问题,可以采用敏感性分析方法(sensitivity analysis method),在众多特征参数中,找到对于振动特性起主要作用的特征参数,忽略次要参数。
特征敏感性(characteristic sensitivity)[84]是根据系统结构特征参数(特征值λ和特征矢量φ)对结构参数p的改变率,定义特征值敏感性∂λ/∂p和特征矢量敏感性∂φ/∂p。
敏感性分析物理概念明确,可用直接求导法(direct derivation)推导(见图13)。
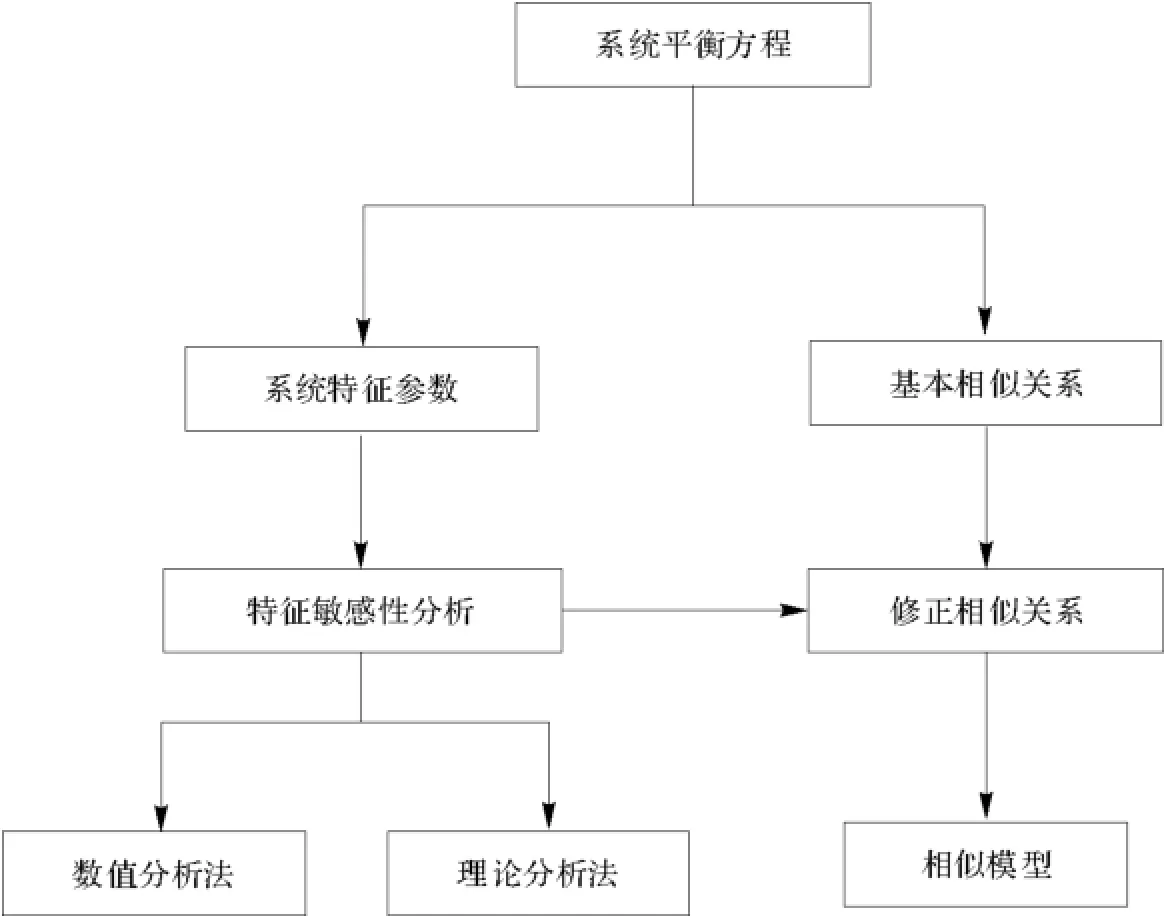
图13 基于敏感性分析建立相似关系流程Fig.13 Flow chart of establishing scaling laws based on sensitivity analysis
几何参数和材料参数对于弹性薄板固有特性的影响,可使用理论分析法(theoretical analysis method)和数值分析法(numerical analysis method),对固有特性敏感性进行分析对比,突出主要因素,忽略次要因素,扩大弹性薄板材料的选择范围,降低加工难度和精度要求,提高实验可行性。
4.1.1 基于理论分析法的敏感性分析
结构振动系统的运动方程可以表述为如下形式。

式中,M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;w0为位移。
若方程的解可以表述为如下形式

式中,λj为方程特征值;φj为特征函数;t为时间。
则可将式(61)代入式(60),得到如下结果。

另有

联立式(63)和式(62),可得如下结果。
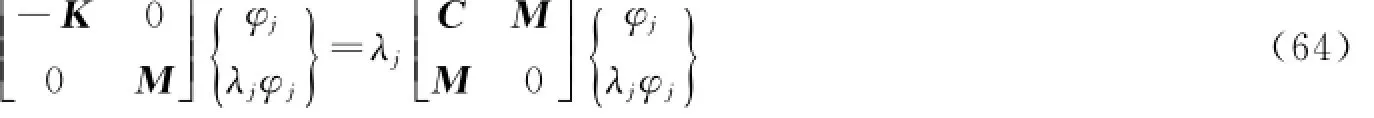
式(64)可简写为如下形式。

式(62)对结构参数p求导,可以得到如下结果。
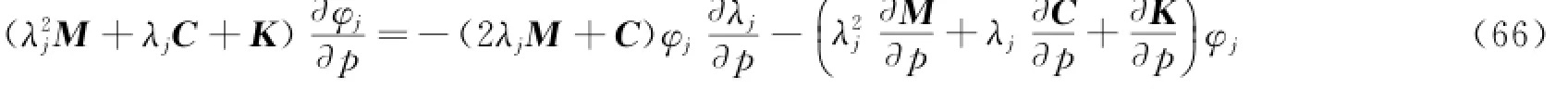
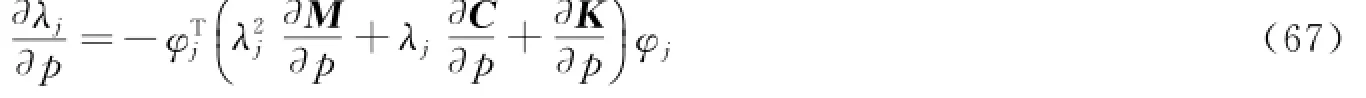
由正交条件,可知

即

求导后,可得如下结果。
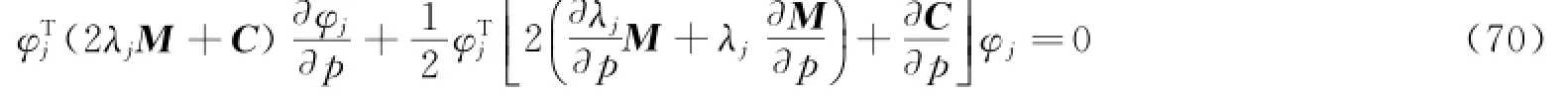
联立式(69)和式(70),可得如下结果。
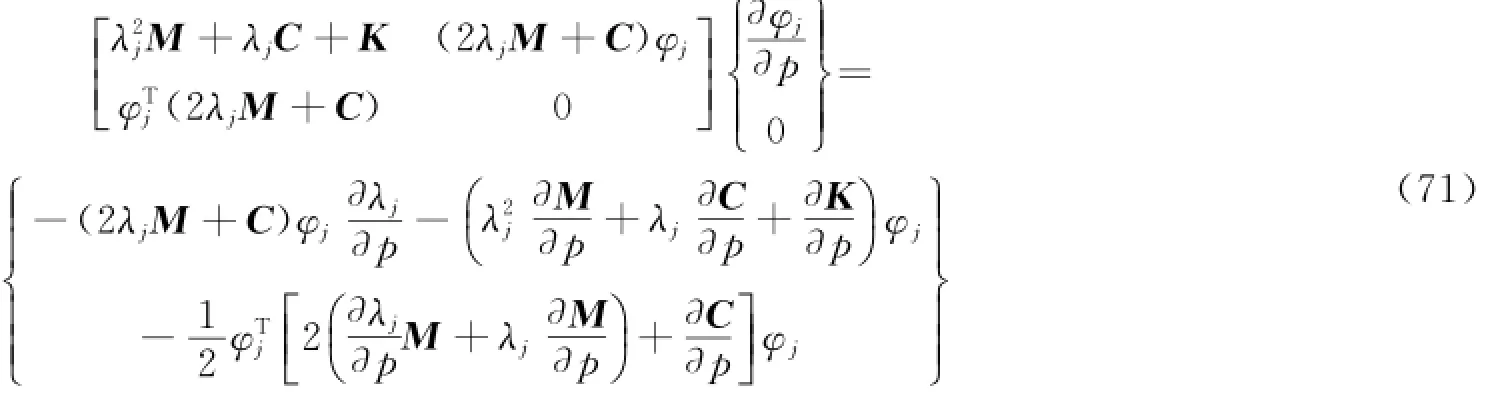
式(71)可以简写为如下形式。

从而得到如下结果。

如果特征值λ是m次重根,对应m个振型,结构参数发生变化时,振型的变化要对应与m个不同的模态,否则振型就会发生跳跃。
基于文献[87],振动结构的运动方程可表现为如下形式。
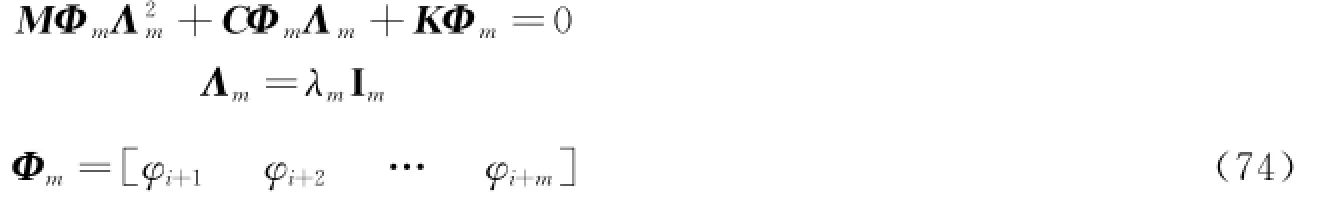
式中,Φm为特征值λm的特征向量矩阵;Im为单位矩阵。在重特征值情况下

对Φm进行正交变换

式中,T为正交变换矩阵。
式(76)可以变换为如下形式。

对p进行求导,可得
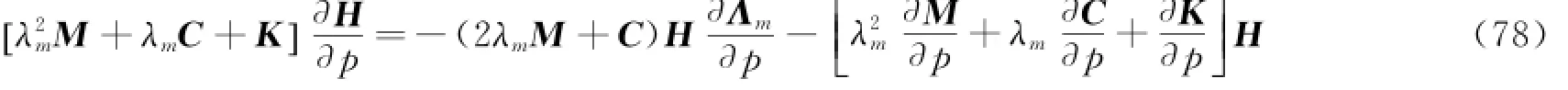
式(78)左右两边同乘以ΦTm,并将式(76)代入,可得
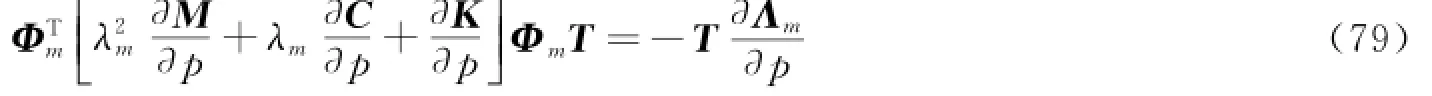
将式(75)两端对参数p求导,可得

式(81)可简写为如下形式。
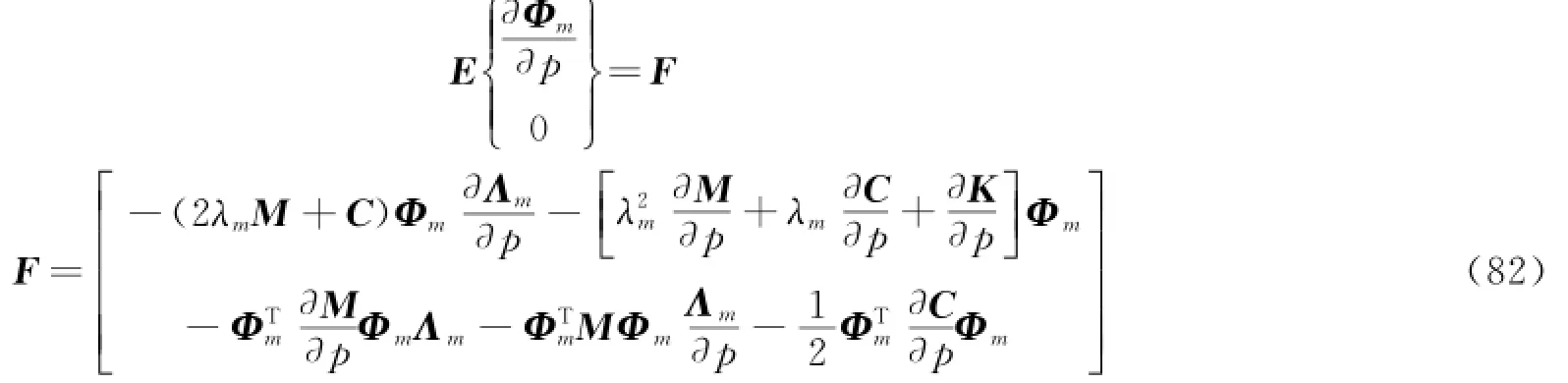
故而

4.1.2 基于理论分析法的敏感性分析算例
利用敏感性分析的理论表达式对弹性薄板特征参数进行分析,以指导不完全相似模型的设计。
【任务要求】 通过矩形弹性薄板实例,对其长度,宽度,厚度及泊松比的敏感性,运用基于理论分析法的敏感性分析进行分析。
在无阻尼的情况下,即阻尼比矩阵C=0,对于悬臂矩形板,运用MATLAB编制程序,进行敏感性分析。使用平面矩形单元和矩形弯曲单元组成的复合单元建立了弹性薄板的有限元模型(见图14),共有100个单元,每个单元有5个自由度(沿x方向的位移u,沿y方向的位移v,沿z方向的位移w,以及绕x轴的转角θx,绕y轴的转角θy),共有605个自由度。
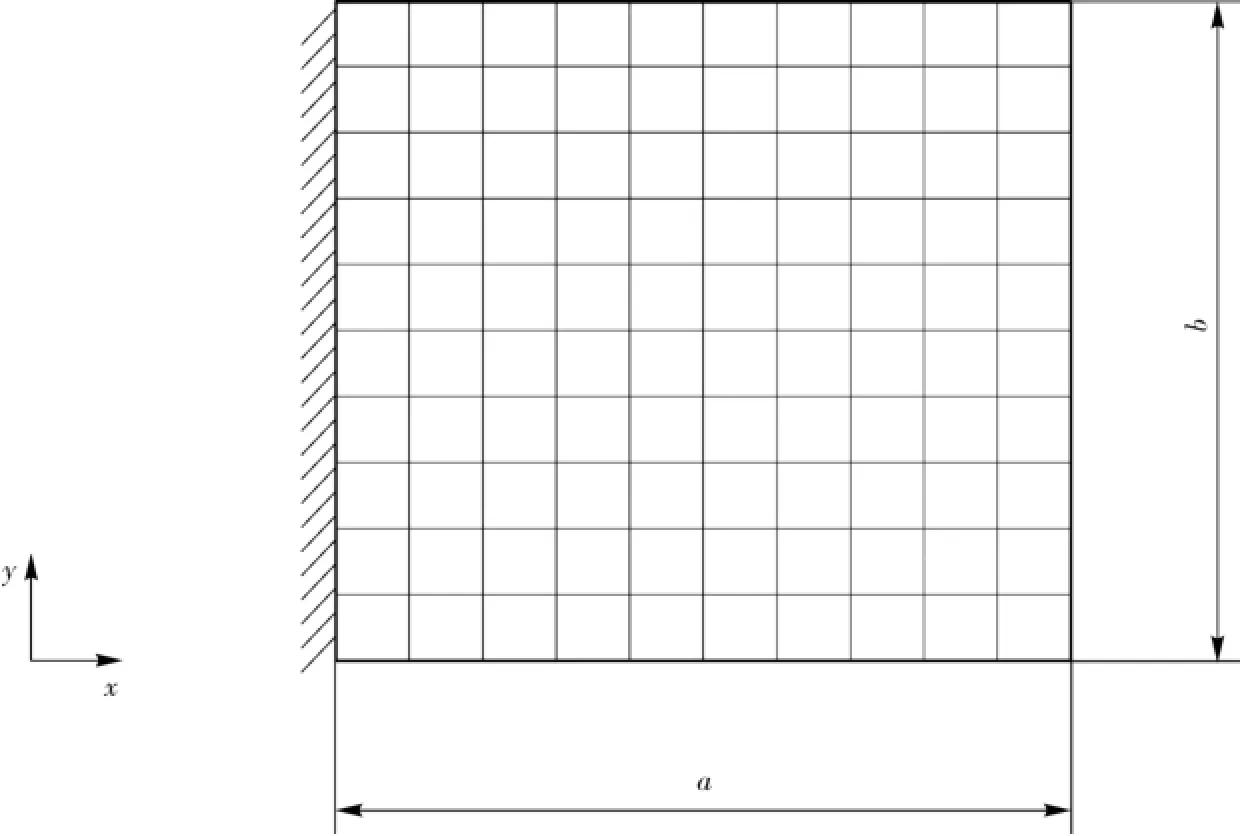
图14 弹性悬臂薄板的有限元模型Fig.14 Finite element model of elastic cantilever thin plate
弹性薄板的几何参数和材料参数见表17,边界条件为一端固定一端自由。分别分析特征值对几何参数和泊松比的敏感性。

表17 弹性薄板的材料及尺寸参数Tab.17 Material and size parameters of thin plate
表18给出了弹性薄板固有频率的MATLAB计算值和ANSYS计算值。分析表明,二者相差很少,说明在求解固有频率的问题上,程序是完全正确的。
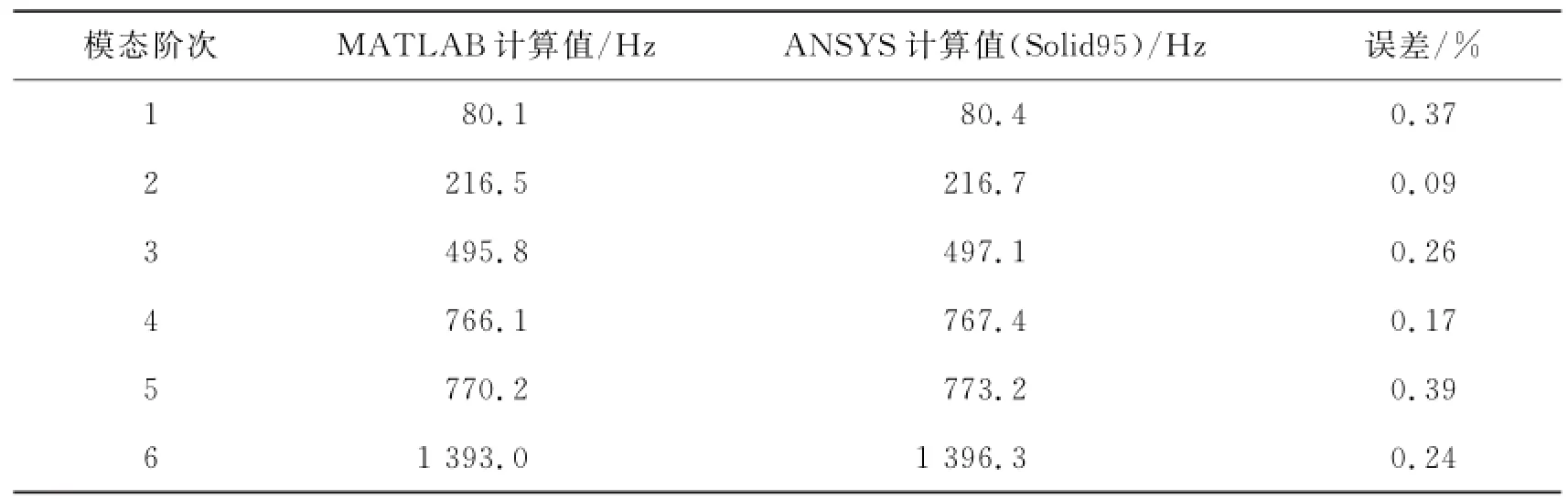
表18 悬臂板的固有频率Tab.18 The natural frequency of cantilever plate
根据式(73)与式(83)对薄板敏感性进行计算,得出了前六阶固有频率对厚度、长度、宽度、泊松比的敏感性(见表19)。

表19 结构参数对模态固有频率的敏感性Tab.19 The sensitivity of structural parameters to the modal natural frequency
从表19中可以进行如下判读。
【判读7】 弹性薄板的固有频率对厚度的变化最敏感,随着厚度的增加固有频率逐渐增加,且随着阶次的提高,数值的增幅变大。
【判读8】 弹性薄板的固有频率对泊松比的变化最不敏感。
【判读9】 在弯曲和扭转振动时,固有频率对长度的敏感性要高于对宽度的敏感性,随着这两个参数的增加,固有频率减小,减小的幅度随着阶次的增加而逐渐变大。
【判读10】 在弦向振动时,固有频率对宽度的敏感性要高于对长度的敏感性。
主振型对几何参数和物理参数的敏感性,可以用一个多维向量表示,但维数太高往往无法表示,例如,图15中的敏感性向量高达605维,不易表示。
为了清楚地表示出主振型,可以在振型向量前乘以一个很大的系数。由此思路出发,提出了前六阶主振型对长度的敏感性曲面(见图15)。

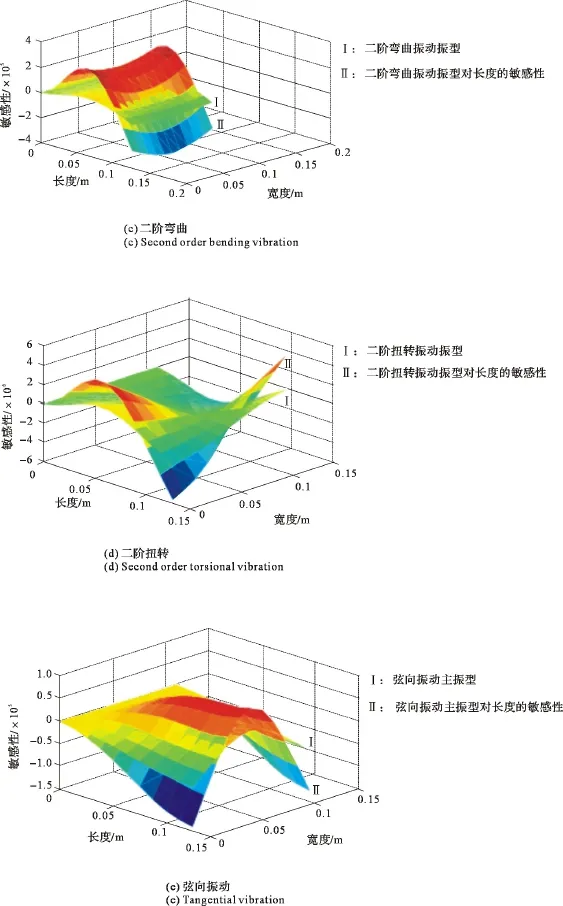

0主振型对厚度的敏感性Fig.15 Sensitivity of main modes to thickness
对比薄板振型与敏感性曲面,二者的图像完全相同。可知弹性薄板上某一点振幅对几何参数的敏感性与其相对位移有关,相对位移越大敏感性越高,这与文献[88]的结论相符。
4.1.3 基于数理统计的敏感性分析
敏感性分析除采用理论分析法外,还可采用统计方法。
【假定4】 输入参数是具有真实分布的随机变量,将按参数的每一个取值进行一次模拟计算,在足够多的模拟后,综合考虑输入参数的变化对结果的影响。
文献[89]介绍了ANSYS的PDS(Probabilistic Design System,概率设计系统)模块的基本原理。
【定义18】 有样本x1,x2,…,xn,将样本单元从小到大排列成x(1),x(2),…,x(n)。若xi=x(Ri),则称xi(i=1,2,…,n)在样本x1,x2,…,xn中的秩为Ri,Ri=1,2,…,n。
由“定义18”出发,可以看出,xi的秩Ri即为xi在整个样本序列中按从小到大顺序排列的位次号。
【定义19】 若有数据对{x1,y1}T,{x2,y2}T,…,{xn,yn}T,则yi(i=1,2,…,n)在样本y1,y2,…,yn中的秩为Qi,Qi=1,2,…,n。
【定义21】 Spearman秩相关系数
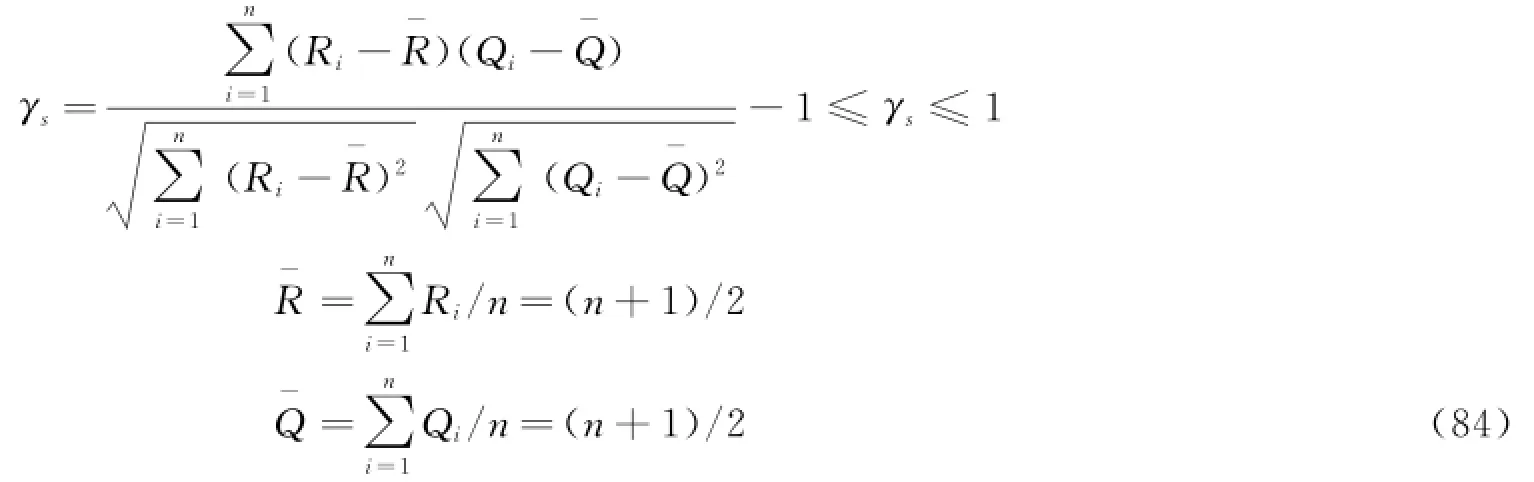
Spearman秩相关系数检验法是非参数统计中用来检验变量之间相关程度的重要方法,其秩相关系数取值范围为[-1,1],有以下特征。
【特征1】 当两变量之间存在单调递增关系时,相关系数为正(+1.00表示完全正相关)。
【特征2】 当两变量之间存在单调递减关系时,相关系数为负(-1.00表示完全负相关)。
【特征3】 当两变量之间没有关系时,相关系数为0。
【特征4】 相关系数绝对值越大,表明两变量的相关性越大。
ANSYS的PDS设计模块分析中,分析输入参数的不确定性对于系统输出的变量的影响程度的常用概率分析方法有蒙特卡罗法(Monte Carlo method)和响应面法(response surface method),关于它们的详细介绍可参考文献[90-92]。ANSYS敏感性表示方法采用Spearman秩相关系数。
4.1.4 基于数理统计的敏感性分析算例
利用敏感性分析的统计分析方法,可以对弹性薄板特征参数进行分析,指导不完全相似模型的设计。【任务要求】 对图11所示矩形板,对其长度,宽度,厚度及泊松比的敏感性,运用统计方法进行分析。
弹性薄板的支承方式为悬臂形式,长度a服从均匀分布U(105 mm,155 mm),宽度b服从均匀分布U(90 mm,130 mm),厚度h服从均匀分布U(0.5 mm,2.5 mm),泊松比服从均匀分布U(0.2,0.3),讨论以上参数对前六阶模态的影响,取样次数为10 000次。
由ANSYS的PDS设计模块分析,图16中的4个图像清楚地表示厚度h,长度a,宽度b,泊松比μ的抽样分布情况,均接近均匀分布,表明抽样次数足够多,抽样试验是有效的。
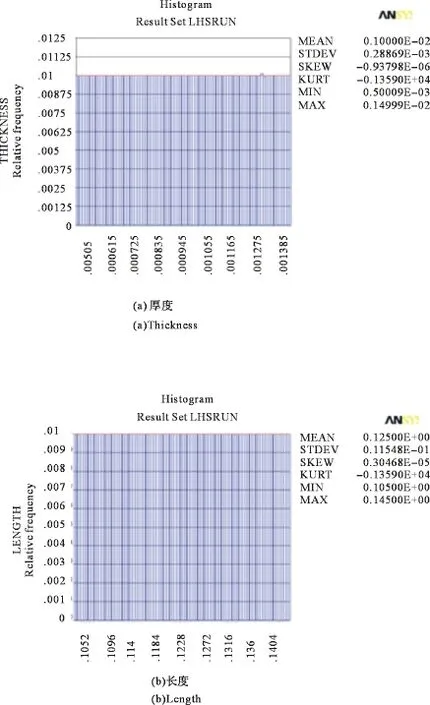
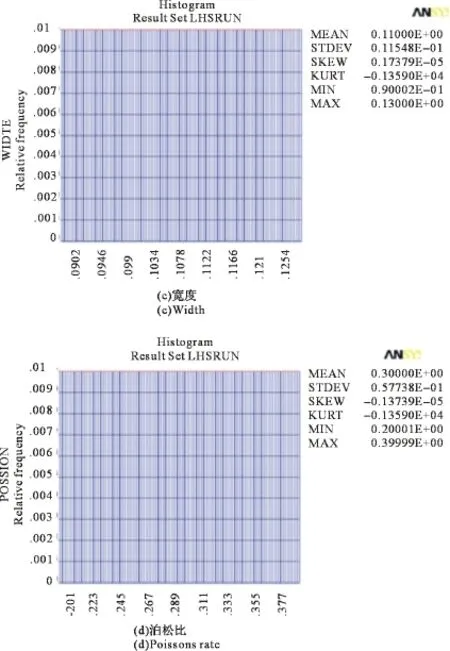
图16 结构参数的抽样柱状图Fig.16 Sampling histogram of structural parameters
表20列出了前6阶固有频率的敏感性,可以看出固有频率随着弹性薄板厚度h的增加而迅速增加,随着长度a的增加而减少,随着宽度b的增加而减少。在上述参数中,厚度h对固有频率的影响最大,泊松比μ的影响最小,跟其他变量相比差一个数量级,可以忽略不计,宽度a和长度b对固有频率均有不同程度影响,在设计模型时需要考虑它们的影响。
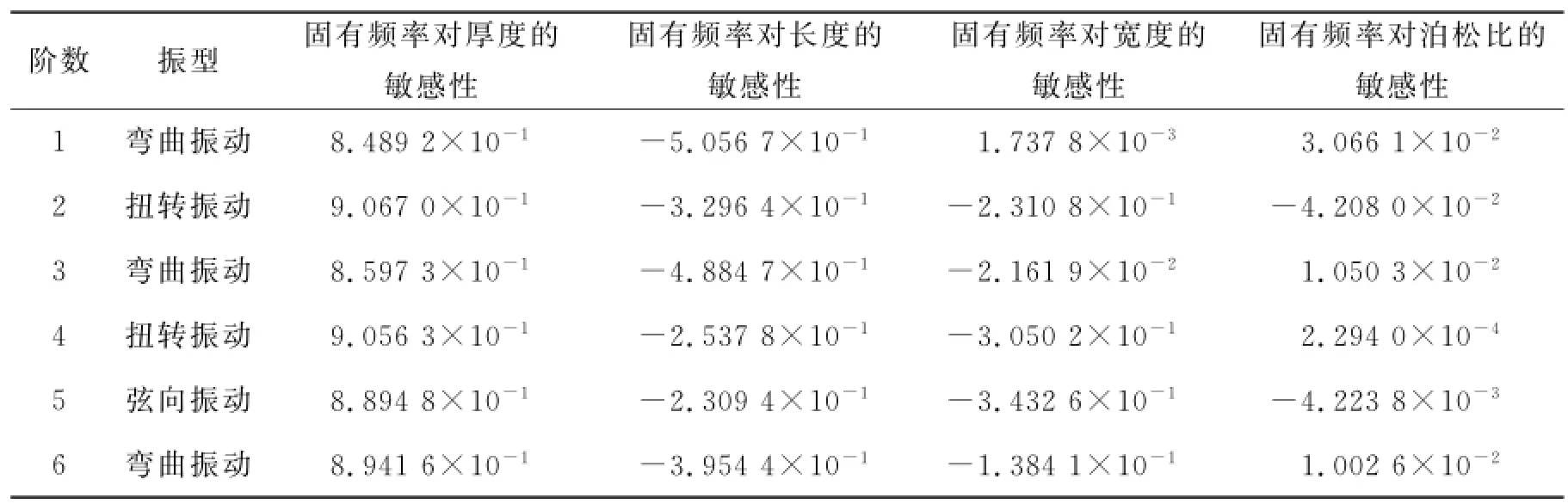
表20 固有频率对结构参数的敏感性Tab.20 The sensitivity of structural parameters to the modal natural frequency
针对弹性薄板的固有频率和主振型对几何参数和材料参数的敏感性进行分析对比,可以发现:
【判读11】 固有频率均随着厚度h的增加而迅速增加,随着长度a的增加而减少,随着宽度b的增加而减少;厚度h的影响最大,泊松比μ的影响最小,长度a和宽度b的影响不可忽略。
【判读12】 理论分析方法与统计分析方法的结果也存在不同点,数值分析各敏感性值并不是随着参数的增加而迅速增加,这是由于Spearman秩相关系数是一个定性的比值,并不能如理论分析的那样定量表示出在几何参数发生变化时,明确地表示固有频率的变化量。
【判读13】 在分析固有频率对泊松比的敏感性时,出现的不一致,是由于数值很小,数值分析误差造成的。
从理论分析和数值分析出发,通过分析固有频率和主振型对几何参数和材料参数的敏感性,并进行对比,可以得出以下结论。
【结论5】 弹性薄板固有频率对厚度的变化最为敏感,随着薄板厚度的增加固有频率逐渐增加,且随着阶次提高,数值的增幅也增加;而对泊松比的变化最不敏感。
【结论6】 弯曲振动和扭转振动对长度的敏感性要高于对于宽度的敏感性,随着这两个参数的增加,固有频率减小,减小幅度随着阶次的增加而逐渐变大。
【结论7】 在弦向振动时,对于宽度的敏感性要高于对于长度的敏感性。厚度的影响最大,泊松比的影响非常小,可以忽略不计,长度和宽度的影响较小,但是不可忽略。
【结论8】 弹性薄板的振型中某一点的振幅对于几何参数的敏感性与其相对位移有关,相对位移越大敏感性越高,每阶敏感性曲面与其主振型是相同的。
【结论9】 泊松比对于预测的精度相比其他的参数非常小,进一步验证了泊松比具有自相似性。
【结论10】 弹性模量和密度等参量已在相关数学模型算式中得到反映,材料并不是影响振动相似的因素,而几何相似是影响动力学相似的条件。
由上述结论可得以下相似规则。
【相似规则4】 在模型的设计和制造过程中,应控制厚度的制造误差,保证其加工精度,针对不同的模态,对宽度和长度进行取舍。
4.2 畸变修正基本理论
在实际模型设计时,常常会因为一些物理量满足不了相似关系要求而产生畸变。为了利用畸变模型(distorted model)的试验结果预测原型特性,往往需要进行修正。
4.2.1 畸变修正
畸变的存在对于预测原型的动力学特性会产生很重要的影响,因此,畸变修正显得非常重要。
【定义22 基准模型(basic model)】 以主导参数(如重要几何参数)的缩比为相似关系,建立的与原型完全几何相似的模型。
【任务要求】 以弹性薄板模型与原型的长度缩比为相似关系,建立基准模型;以基准模型为媒介,再进行基准模型和实际模型畸变分析,最终获得畸变模型和原型之间的畸变系数和预测系数的函数关系。以预测弹性薄板的固有频率为例,具体步骤如下。
【step 1】 定义畸变模型和原型的固有频率畸变系数。

式中,δj为畸变模型与原型的固有频率畸变系数;ωim为模型板第i阶固有频率;ωip为原型板第i阶固有频率;j为模态阶次。
【step 2】 对几何尺寸进行归一化处理。
式(85)可以简写为如下形式。

式中,xm为模型的长厚比;xp为原型的长厚比;yhm为模型的宽厚比;yhp为原型的宽厚比;g,r,l和k为系数。
【step 3】 采用数值仿真通过多项式拟合得到系数g,r,l和k,计算固有频率相似比。
根据以上论述,可以建构畸变修正基本流程框架(见图17)。
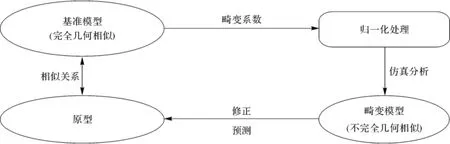
图17 原型与模型关系Fig.17 Relationship between prototype and models
4.2.2 算例
【任务要求】 利用数值分析方法分析基准模型与畸变模型的频率变化关系,建立频率变化方程,对原型固有频率进行预测。
【设定】 弹性薄板畸变模型,其薄板厚度均为2 mm,弹性模量为212 GPa,泊松比为0.3,密度为7 870 kg/m3;其长厚比x-和宽厚比y-在20~100范围内变化。
为了简化说明图17的应用方法,选取4种常见模态进行分析。利用ANSYS仿真分析分别计算不同x-,y-时的薄板固有频率值,通过二元多项式拟合得到4种模态多项式形式的表达式。
【模态1】 对于一阶弯曲振动固有频率ωB1。
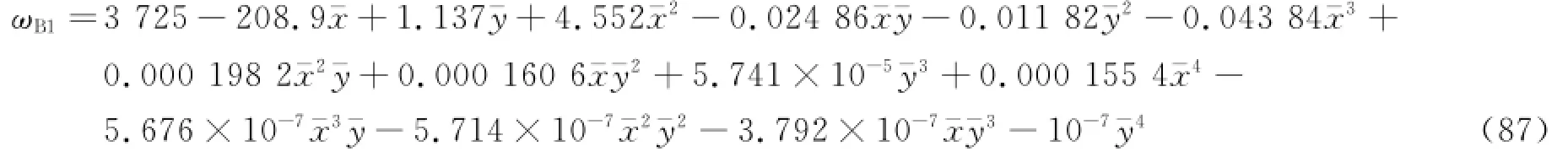
其拟合曲面见图18。
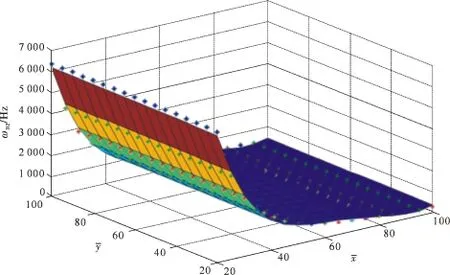
图18 不同长厚比和宽厚比时,一阶弯曲振动的固有频率拟合曲面Fig.18 Natural frequency fitting surface of the first order bending vibration with different slenderness ratio and width-to-thickness ratio
【模态2】 对于二阶弯曲振动固有频率ωB2。
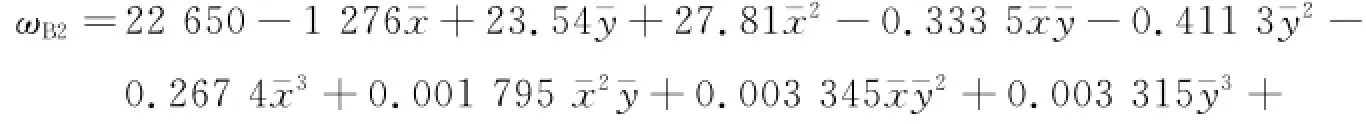
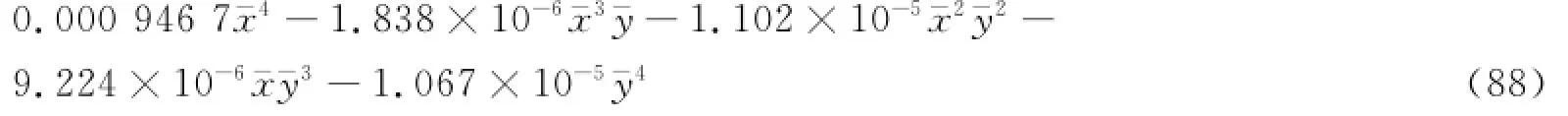
其拟合曲面见图19。
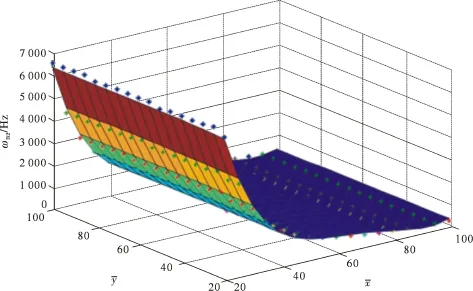
图19 不同长厚比和宽厚比时,二阶弯曲振动的固有频率拟合曲面Fig.19 Natural frequency fitting sur face of second-order bending vibration with different slenderness ratio and width-to-thickness ratio
【模态3】 对于一阶扭转振动固有频率ωT1。
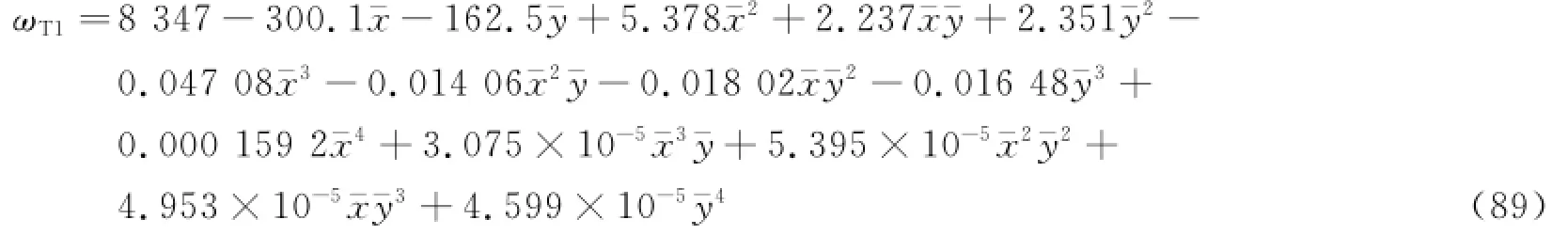
其拟合曲面见图20。

图20 不同长厚比和宽厚比下,一阶扭转振动的固有频率拟合曲面Fig.20 Natural frequency fitting surface of first-order torsional vibration with different slenderness ratio and width-to-thickness ratio
【模态4】 对于二阶扭转振动固有频率ωT2。
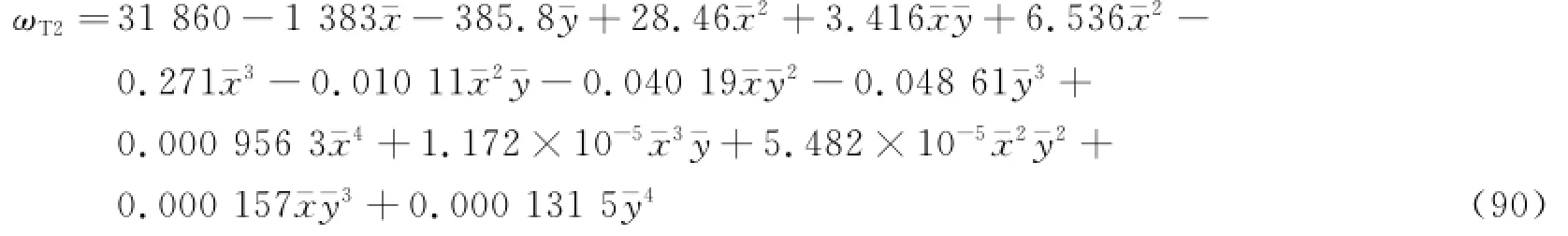
其拟合曲面见图21。
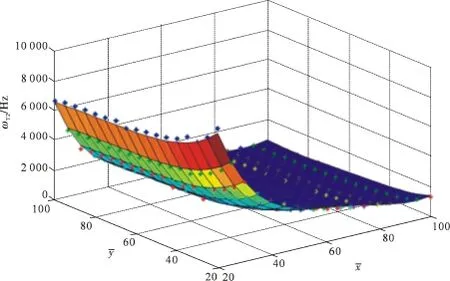
图21 不同长厚比和宽厚比下,二阶扭转振动的固有频率拟合曲面Fig.21 Natural frequency fitting surface of second-order torsional vibration with different slenderness ratio and width-to-thickness ratio
由式(49)可知,与原型完全相似的基准模型和原型固有频率有如下关系。

式中,ω0p为与原型完全相似的基准模型的固有频率;ωp为原型的固有频率;h0p为与原型完全相似的基准模型的厚度;hp为原型的厚度;E0p为与原型完全相似的基准模型的弹性模量;Ep为原型的弹性模量;ρ0p为与原型完全相似的基准模型的密度;ρp为原型的密度。
与畸变模型完全相似的基准模型和畸变模型的固有频率有如下关系。

式中,ω0m为与畸变模型完全相似的基准模型的固有频率;ωjm为畸变模型的固有频率。
将式(91)和式(92)左右两端相除,某一模态的固有频率畸变系数可写为如下形式。

式中,j为模态阶次。
至此,已经完全建立起δj与xm,xp,ym,yp的关系,只要知道畸变模型和原型的宽厚比、长厚比和材料参数,就可以通过式(93)求出对应的预测系数δj,实现对原型的模态预测。
4.3 弹性薄板几何适用区间的确定方法
4.3.1 薄板畸变修正的范围区间的确定
在实际操作中满足所有的相似条件,是十分困难的甚至是不可能的,局部相似畸变模型显得更为实用。通过量纲分析法可求得全部的相似判据,在这些相似判据中,有些可以通过实验条件满足,有些则不能够满足,将这些不能满足实验条件的相似判据用其他能够满足实验条件的数值代替——不完全相似,就会造成相似关系的缺失,进而导致模型畸变。对于畸变的模型,为了使其能够满足预期的固有特性,必须对其进行畸变修正。有些时候由于畸变程度不大,可以使其与原型很好的相吻合;有些时候则可能超出预设的修正范围。为此,畸变修正区间的确定显得尤为重要。
笔者以四周简支的弹性薄板为例,对畸变模型的理论依据进行推导,探讨不同情况下的修正区间问题,以验证理论模型的正确性。
对于四周简支的薄板,施加面匀布载荷q(见图22)。
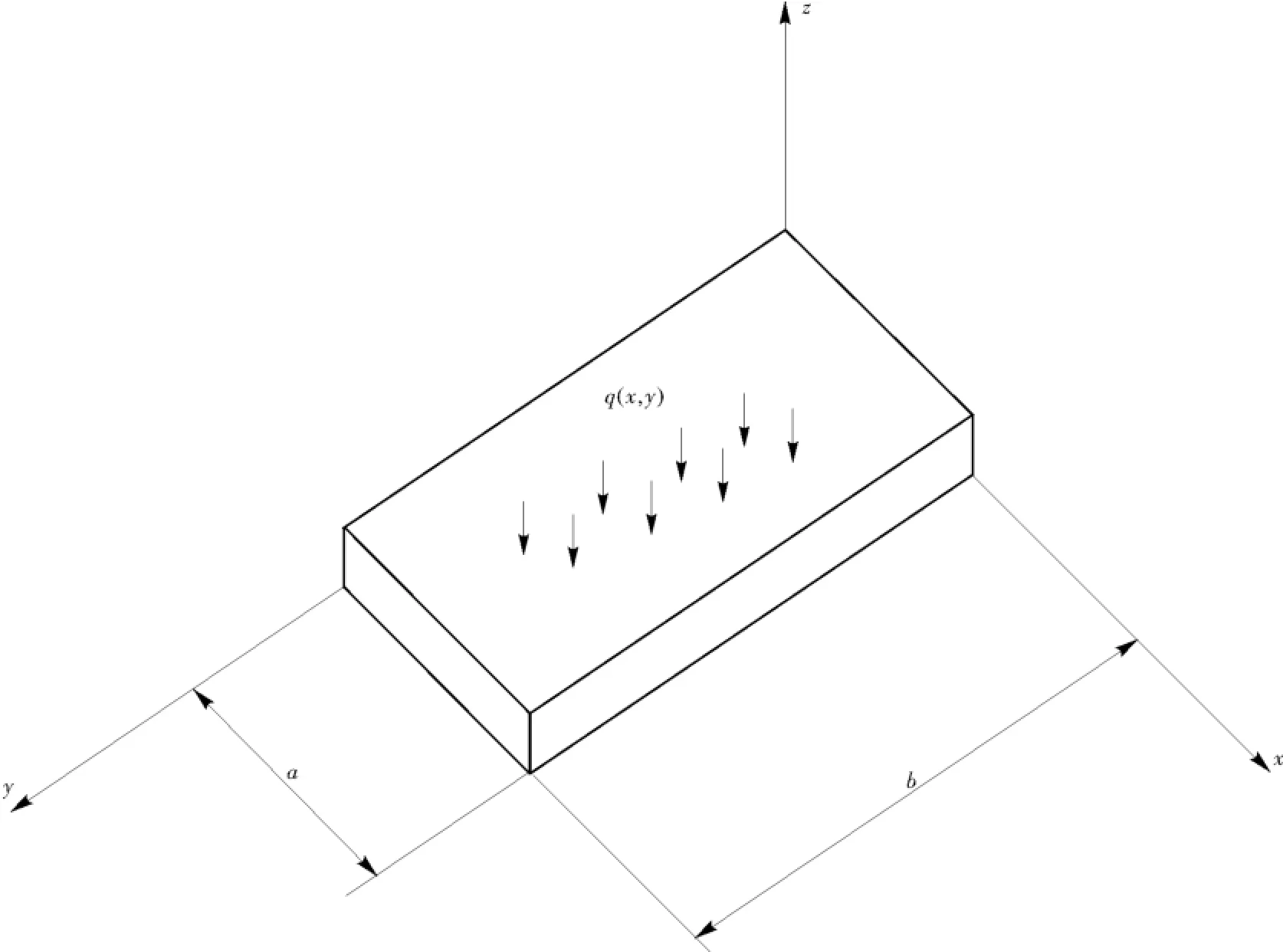
图22 各向同性弹性薄板Fig.22 The isotropic thin
由薄板小挠度弯曲理论可知

x=0与x=a处边界条件如下。

y=0与y=a处边界条件如下。

若存在以下的相似比关系。

式中,λv为相似关系,v为各物理量的符号,如v=a,b,E,等等。考虑原型与模型材料相同,有λE=1。由相似原理可得

令式(98)的前3个表达式分别与第4表达式相等,可得

在完全相似模型中,λx=λy,式(99b)、式(99c)和式(99d)等3个表达式是等价的,但如果因为实验条件导致不能满足λx=λy,则这3个表达式不等价。对于不同的畸变模型,需要找出究竟哪个相似关系能够准确预测原型的行为。
保证λE=λμ=λq=1,令λy=Cλx,C>0,式(99a),式(99b)和式(99c)可写为如下形式。

以具体实例,探讨式(99b),式(99c)和式(99d)的适用性。

给定用于验证上述理论所应用的弹性薄板原型(见表21)及模型的尺寸参数(见表22)。
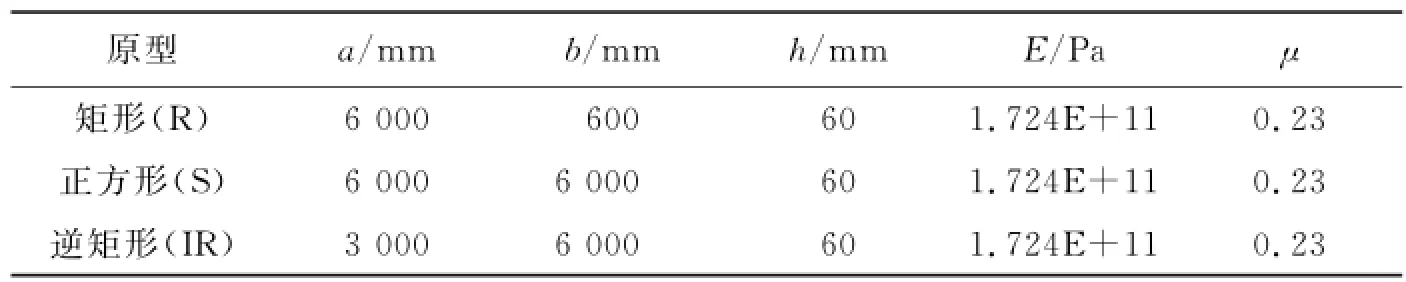
表21 3种原型薄板的尺寸参数Tab.21 size parameters of three prototype thin plates
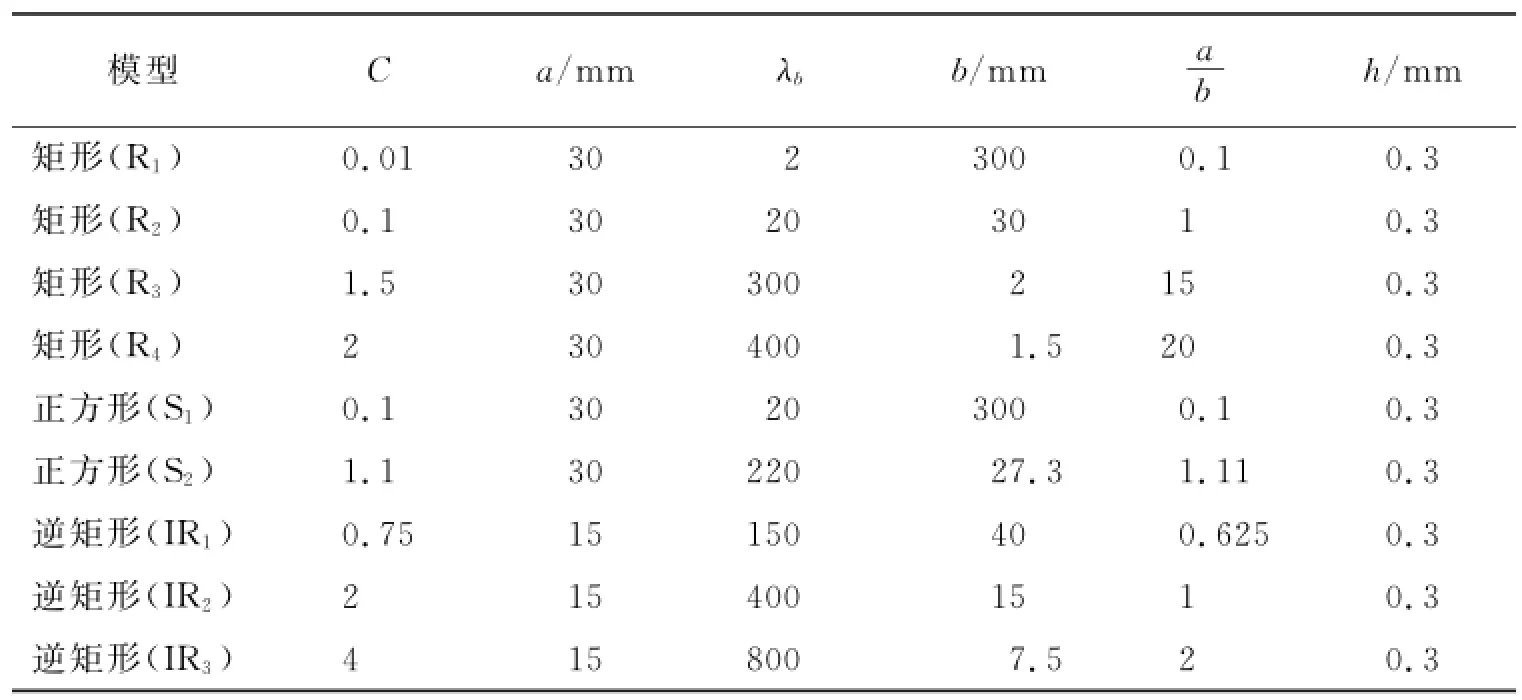
表22 相应模型薄板的尺寸参数Tab.22 size parameters of model thin plates
根据薄板小挠度弯曲理论,薄板受面匀布载荷挠度模型见下式。薄板挠度理论值与实验值见图23。

式中,q0为匀布载荷。
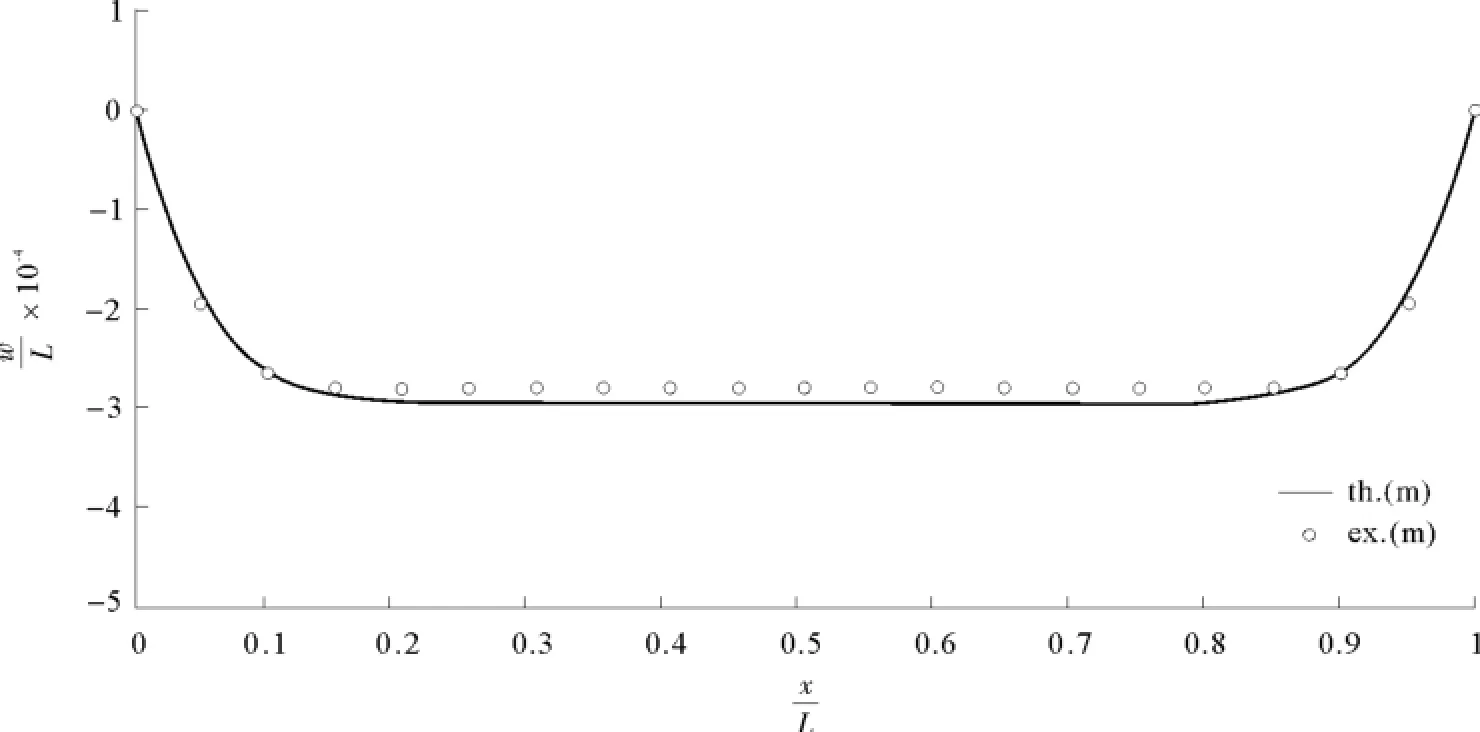
图23 完全相似(C=1)时,板挠度理论值与实验值Fig.23 The predicted and theoretical deflection of plate when complete similarity is C=1
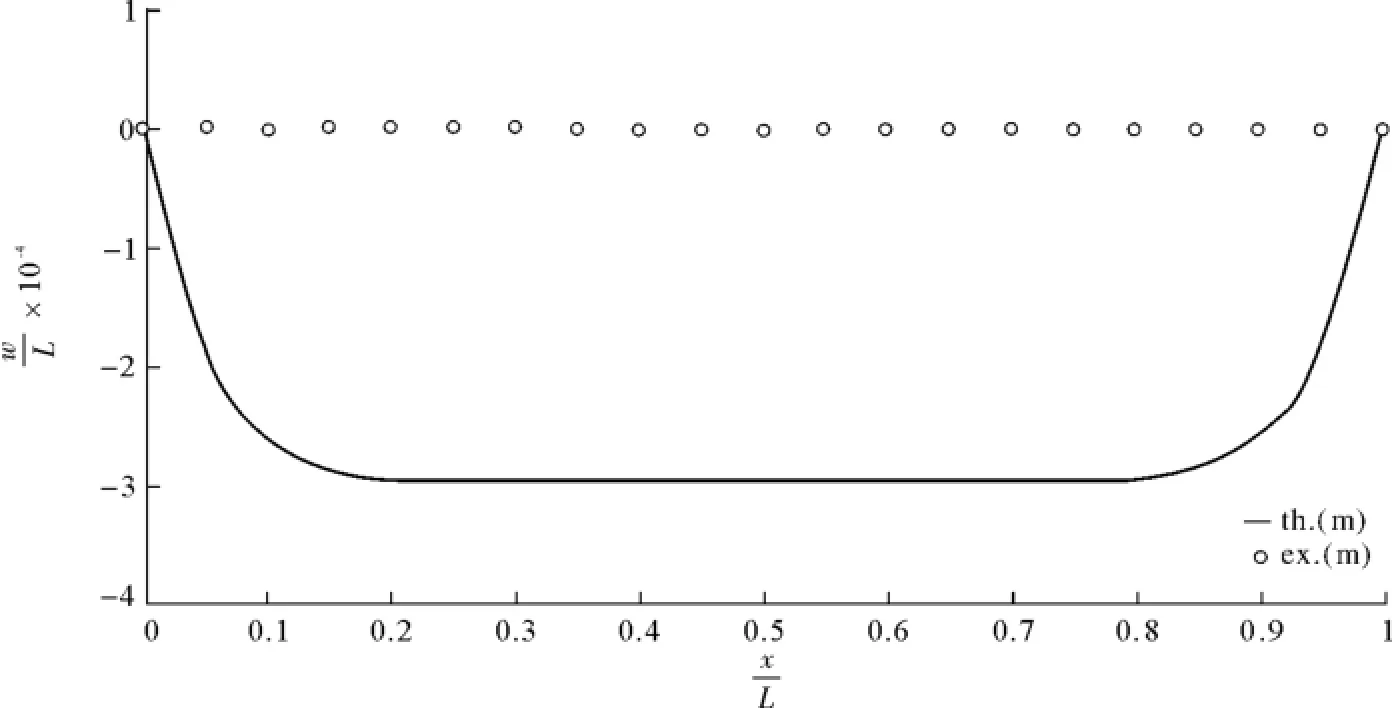
图24 以式(99c)为判据的理论值与模型预测值>1,C=0.01Fig.24 The predicted and theoretical deflection of plate based on Eq(99c),>1,C=0.01
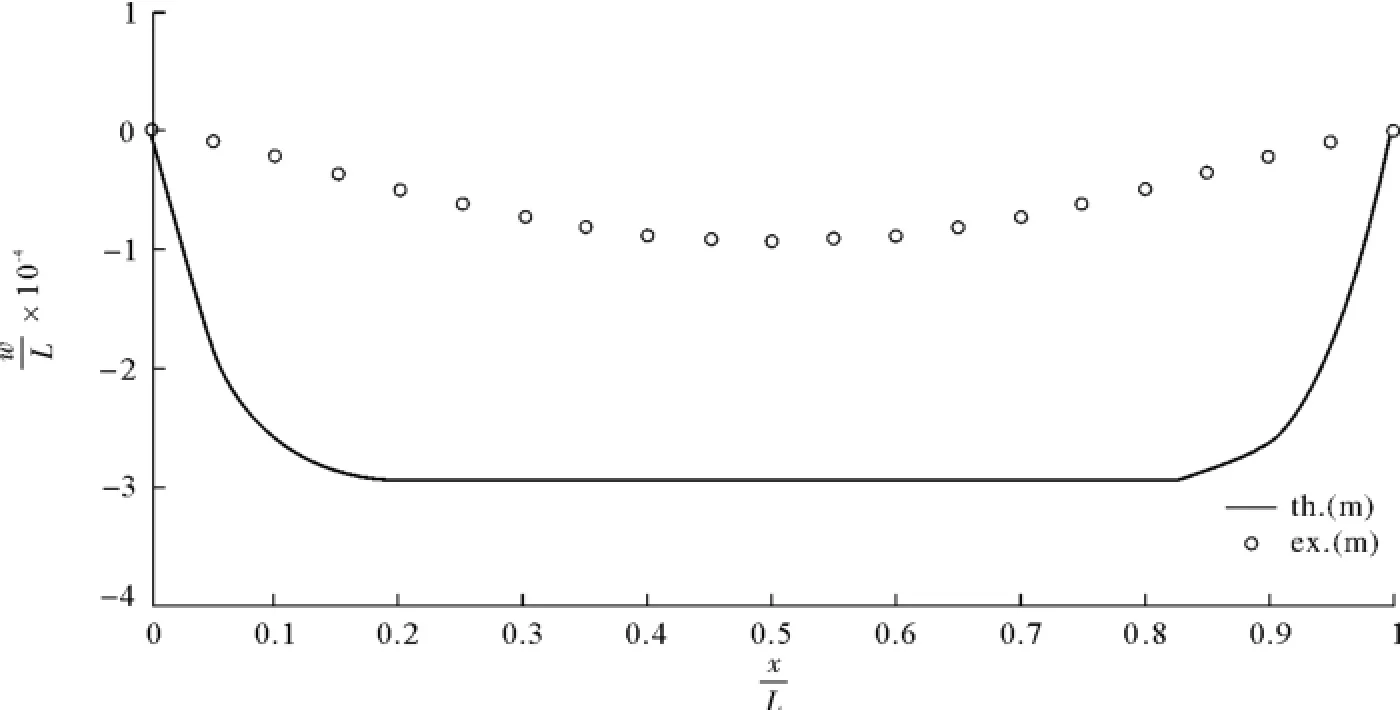
图25 以式(99c)为判据的理论值与模型预测值,>1,C=0.1pFig.25 The predicted and theoretical deflection of plate based on Eq(99c),>1,C=0.1
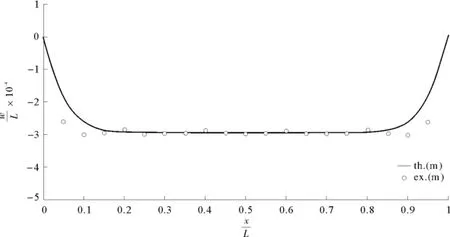
图26 以式(99c)为判据的理论值与模型预测值,>1,C=1.5Fig.26 The predicted and theoretical deflection of plate based on Eq(99c),>1,C=1.5p
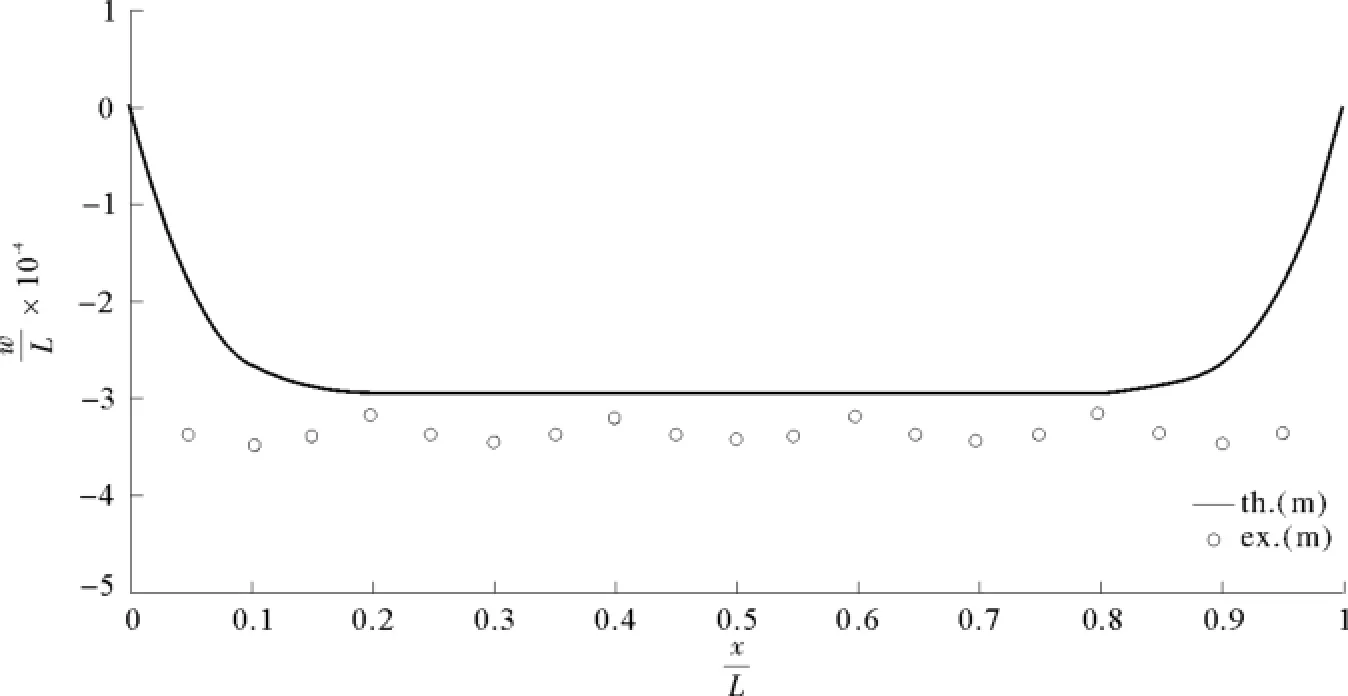
图27 以式(99a)为判据的理论值与模型预测值,>1,C=2Fig.27 The predicted and theoretical deflection of plate based on Eq(99a)>1,C=2
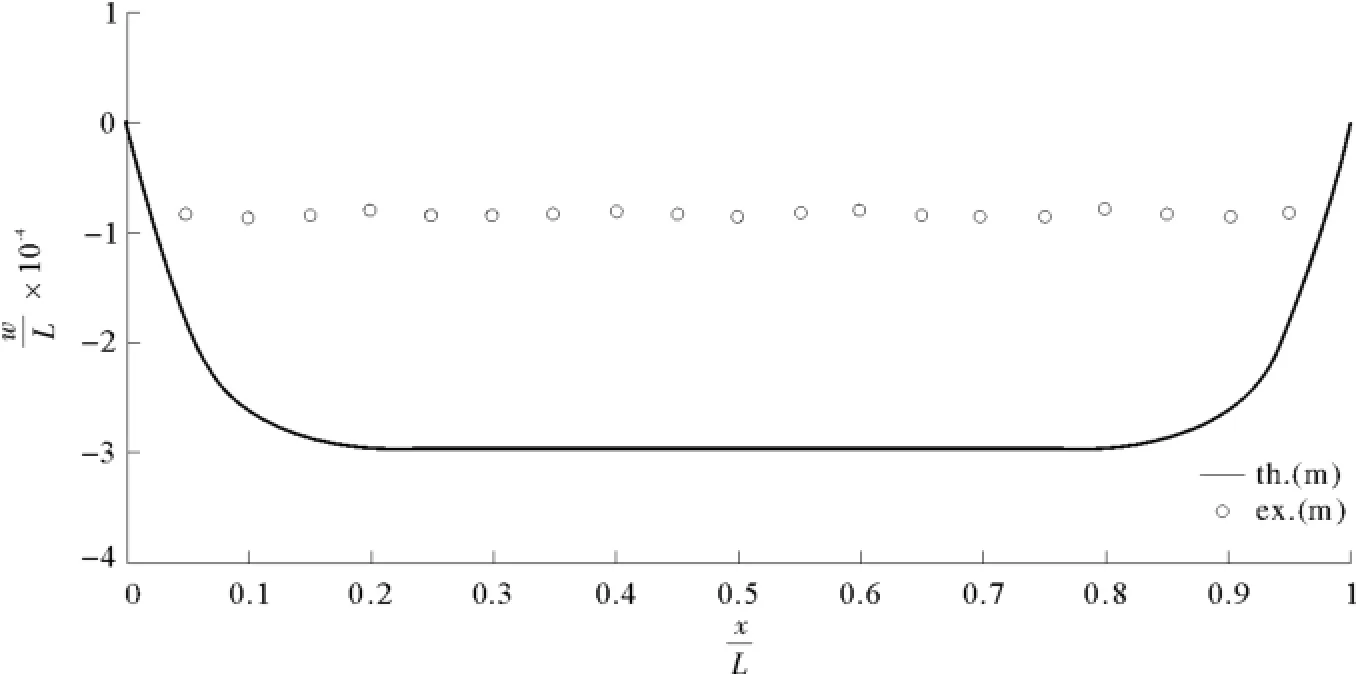
图28 以式(99b)为判据的理论值与模型预测值,>1,C=2Fig.28 The predicted and theoretical deflection of plate based on Eq(99b)>1,C=2
由图24~图28可知,在“情况1”时,C越大,式(85c)的预测值越好;当C→0.01时,式(100c)的预测不准确;在“情况1”下,式(100a)和式(100b)都不适用。
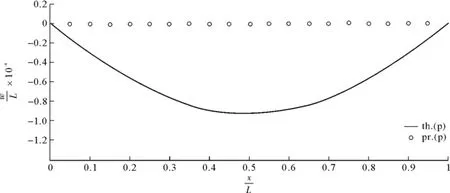
图29 以式(99c)为判据的理论值与模型预测值,=1,C=0.1Fig.29 The predicted and theoretical deflection of plate based on Eq(99c),=1,C=0.1
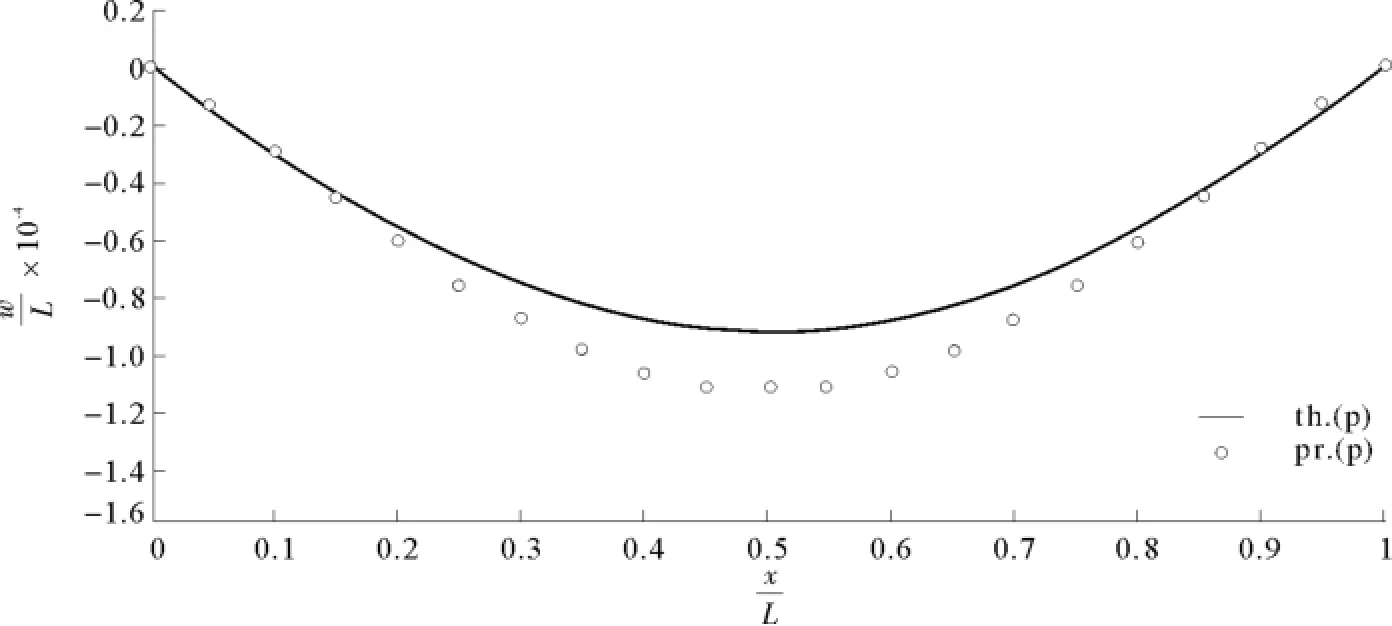
图30 以式(99c)为判据的理论值与模型预测值=1,C=1.1Fig.30 The predicted and theoretical deflection of plate based on Eq(99c),=1,C=1.1
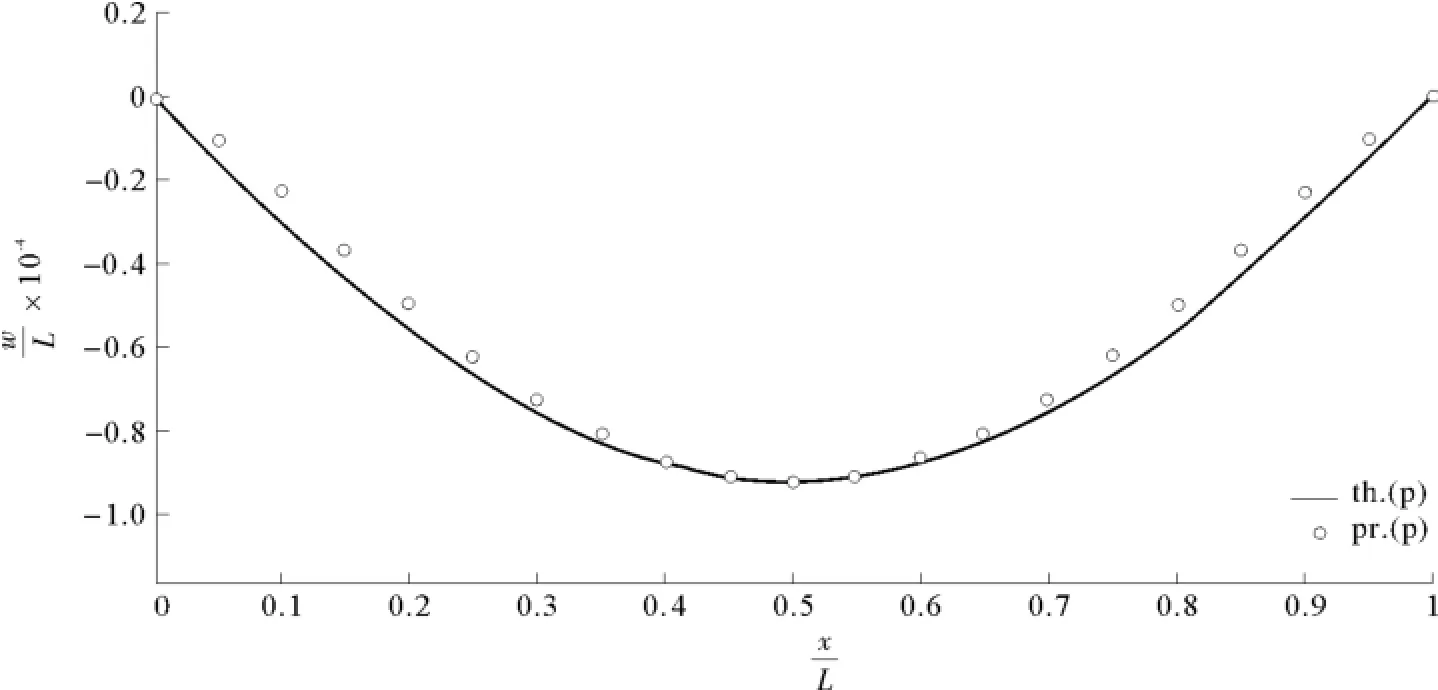
图31 以式(99b)为判据的理论值与模型预测值,=1,C=1.1Fig.31 The predicted and theoretical deflection of plate based on Eq(99b)=1,C=1.1
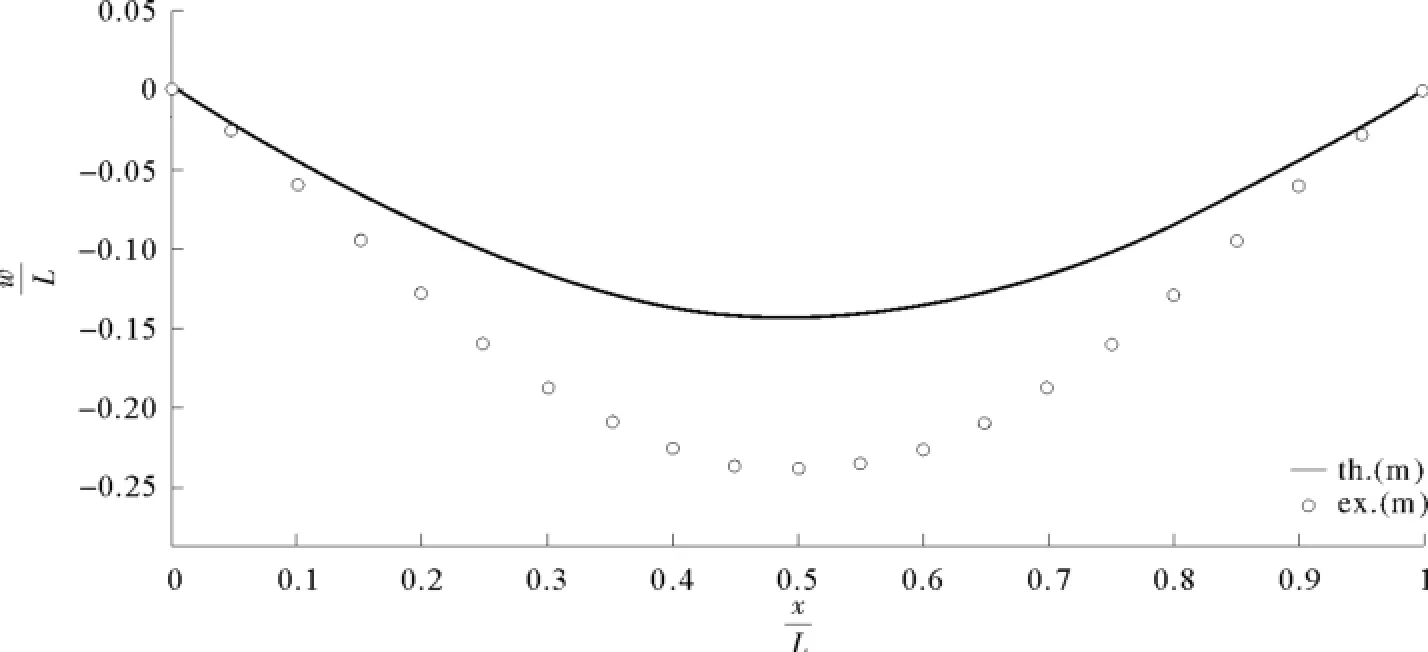
图32 以式(99b)为判据的理论值与模型预测值,<1,C=2Fig.32 The predicted and theoretical deflection of plate,Eq(99b),<1,C=2
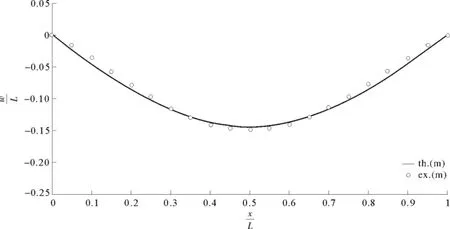
图33 以式(99a)为判据的理论值与模型预测值<1,C=0.75Fig.33 The predicted and theoretical deflection of plate,Eq(99a),<1,C=0.75
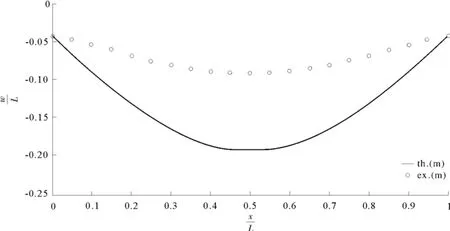
图34 以式(99c)为判据的理论值与模型预测值,<1,C=0.75Fig.34 The predicted and theoretical deflection of plate,Eq(99c),<1,C=0.75
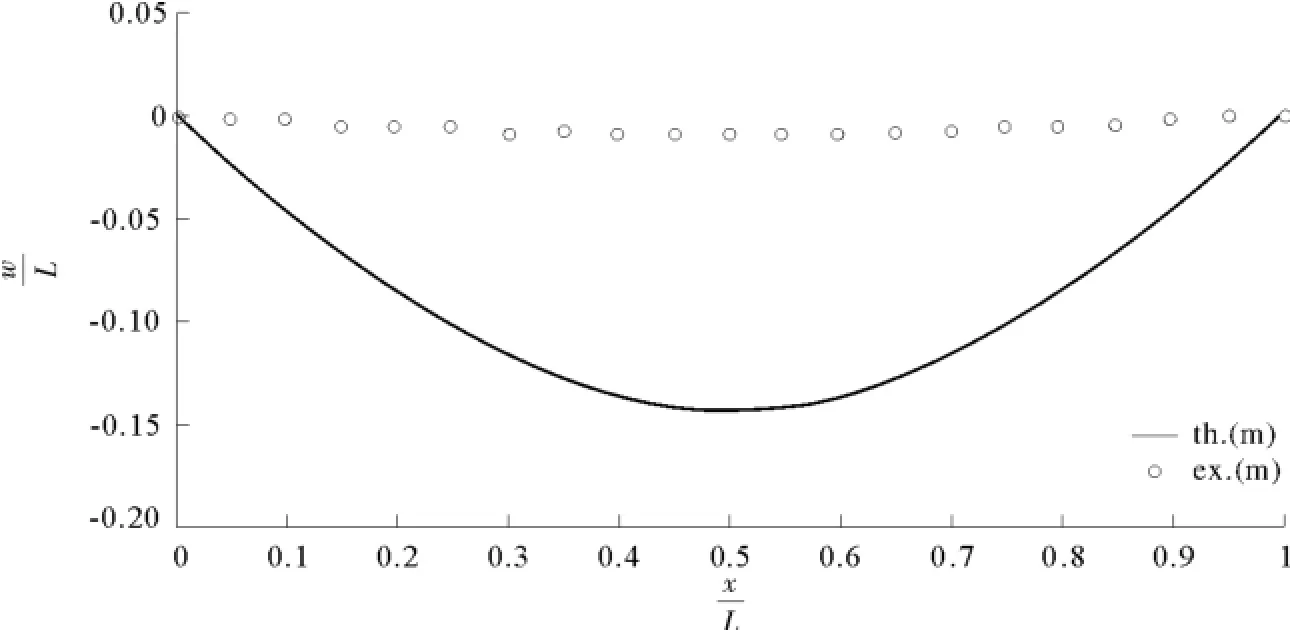
图35 以式(99a)为判据的理论值与模型预测值,<1,C=4Fig.35 The predicted and theoretical deflection of plate,Eq(99a),<1,C=4

图36 以式(99c)为判据的理论值与模型预测值<1,C=4Fig.36 The predicted and theoretical deflection of plate,Eq(99c),<1,C=4
在“情况3”下,式(100b)给出了很好的预测值,而式(100c)和式(100a)则不再适用。
【结论11】 当薄板的几何尺寸发生变化后,应该根据具体的畸变形状,来确定所选取的相似判据。当薄板形状为矩形时,C越大,式(100c)的预测值越好,但C→0.01时,式(100d)的预测不准确,在“情况1”时,式(100c)和式(100b)都不适用。
【结论12】 当薄板形状为正方形时,当模型的长宽比为0.83<<1.2时,式(100b)和式(100a)均有良好的预测效果,但当C→10C→10或C→0.01时,3个判别式的预测都不准确。
【结论13】 当薄板形状为逆矩形时,式(100b)给出了很好的预测值,而式(100c)和式(100d)则不再适用。4.3.2 薄板动力畸变模型几何适用区间的确定
对于弹性模量为E,泊松比为μ,长为a,宽为b,厚度为h的弹性薄板(见图37)。

图37 四边简支的薄板Fig.37 Plate simply supported on four sides
由Kirchhoff假设可知,薄板平衡方程如下。

设板上各点的振型函数为W(x,y),板挠度

式中,A、B为待定常数;ω为固有频率;t为时间。
将式(103)代入式(102),得到振型微分方程。

由对应相似系数相等,可得

式中,λD为刚度相似比;λW为振型函数相似比;λa为长度相似比;λb为宽度相似比;λρ为密度相似比;λω为固有频率相似比。

式中,λh为厚度相似比。
将式(106)代入式(105),可以得到四边简支弹性薄板固有频率的完全相似关系。

对于不完全几何相似模型,λa≠λb≠λh,则λω≠λ-1b,需要确立新的相似关系。设λa=Cλb,C为常数,则相似关系

原型薄板的参数见表23。

表23 原型薄板主要参数Tab.23 Main parameters of prototype plate
为确定式(108a)~式(108c)各相似关系的几何区间,按表23进行分析,以判断几何区间的大致范围,即明确C的大致取值范围(假设模型材料与原型保持相同)。
经过计算,得知原型板的一阶固有频率为17.369 Hz。现分别用5种模型板(见表24),分别通过式(108a)、式(108b)、式(108c)预测原型固有频率,并计算预测误差。一般地,若误差η≤10%,则认为该预测结果是可用的[11],其结果见表25。
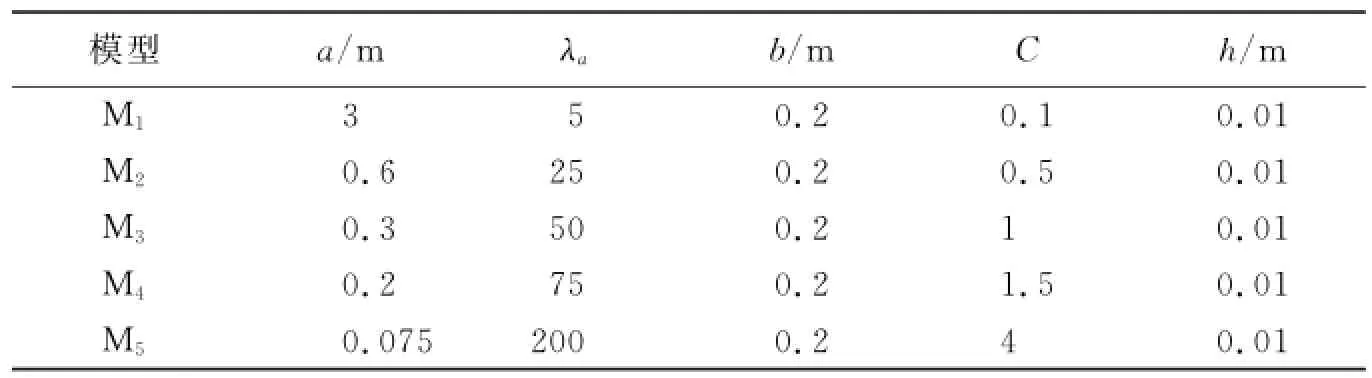
表24 部分模型尺寸参数Tab.24 Size parameters of the model
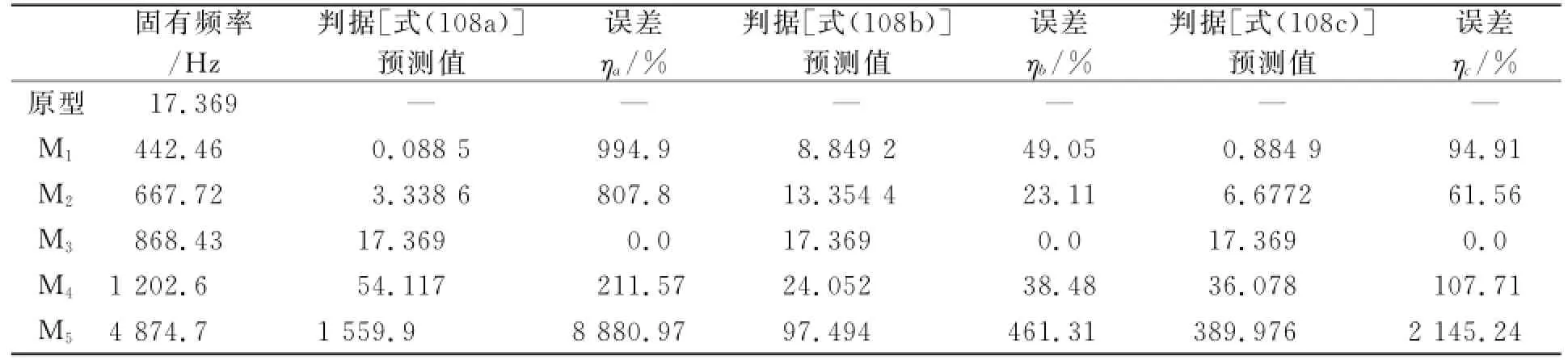
表25 相似关系下得到的理论值、预测值及其误差Tab.25 The theoretical value,predicted value and errors under each scaling laws
对比表25各组数据,得知式(108b)具有较准确的预测结果,可作为弹性薄板固有频率预测的不完全相似关系,同时可知在M2~M4之间存在几何适用区间。
在材料和边界条件相同的条件下,弹性薄板不完全相似的变量为长度a、宽度b和厚度为h。
四边简支弹性薄板的固有频率

式中,ρ0为薄板密度;m*为板长方向的半波数;n*为板宽方向的半波数。
由振型相同的模型与原型的关系,得到以下关系。
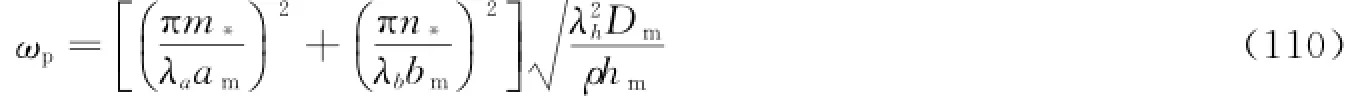
模型板频率解可以表述为以下形式。

式(111)左右两边同乘以式(108b),得到固有频率预测值
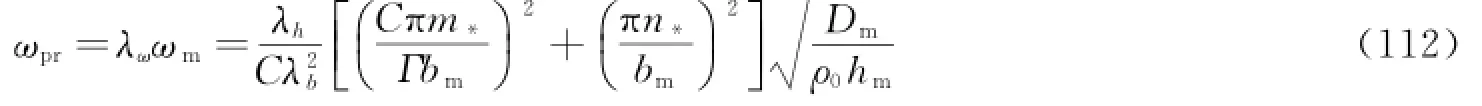
对于不完全几何相似预测误差

将式(111)和式(112)代入式(113),经化简可得
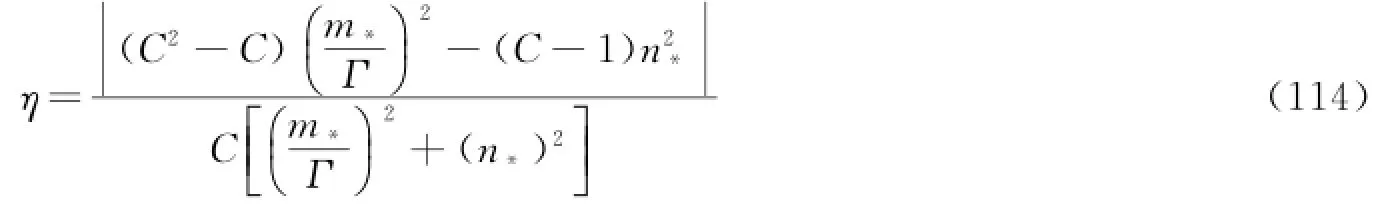
观察式(114)可得到如下结论。
【结论14】 λh是独立的,λh的选择对几何不完全相似关系预测误差没有影响。
【结论15】 影响不完全几何相似预测误差的是C=(λa/λb),λb对几何不完全相似关系的固有频率预测误差没有影响。
【结论16】 原型尺寸a、b的具体值对几何不完全相似的几何适用区间选取没有影响,而影响其区间取值及各阶振型形状的是Γ=(a/b)。
由以上结论可知,分析四边简支弹性薄板的几何适用区间,即为以式(108b)为相似关系,不同Γ值下的C的取值范围。
(1)薄板畸变相似模型几何适用区间的确定
选取a=Γb,b=10 m,h=0.5 m的原型板,若λb=λh=20,材料属性与表23所给原型板相同。
分别选取C=[0.6,0.7,0.95,1.3,1.65,1.95],得到对应的一阶频率预测值在MATLAB中对得到的6个离散预测值采用四阶多项式进行插值运算,得到拟合方程

以0.05为步长,选取更多的离散值对式(112)的适用性进行验证,得到拟合曲线(见图38)。
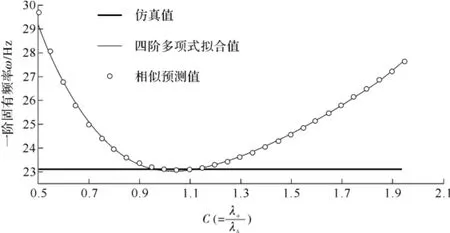
图38 四阶多项式拟合结果验证Fig.38 Verification of fourth-order polynomial fitting results
由图38可知,在C∈[0.6,1.95]范围内,式(115)具有准确的拟合效果。
由η≤10%,将式(116)代入式(114),得到
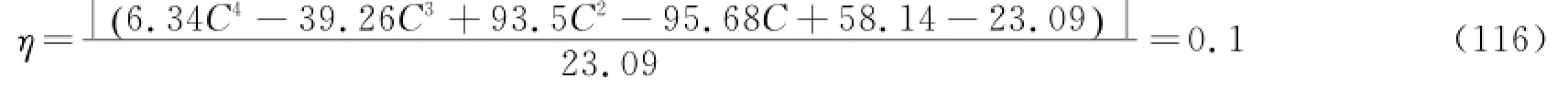
在C∈[0.6,1.95]范围内,解得Cmin=0.675,Cmax=1.646
(2)一阶固有频率几何适用区间边界函数的确定
利用上述方法分别计算Γ=[1,1.1,1.15,1.225]对应的Cmin及Cmax值(见表26),其对应的拟合曲线见图39~图42。取Γ的最大边界值为1.225,是由于高阶频率预测振型控制区间的限制。

表26 不同Γ对应区间边界值表Tab.26 Interval boundary value with differentΓ
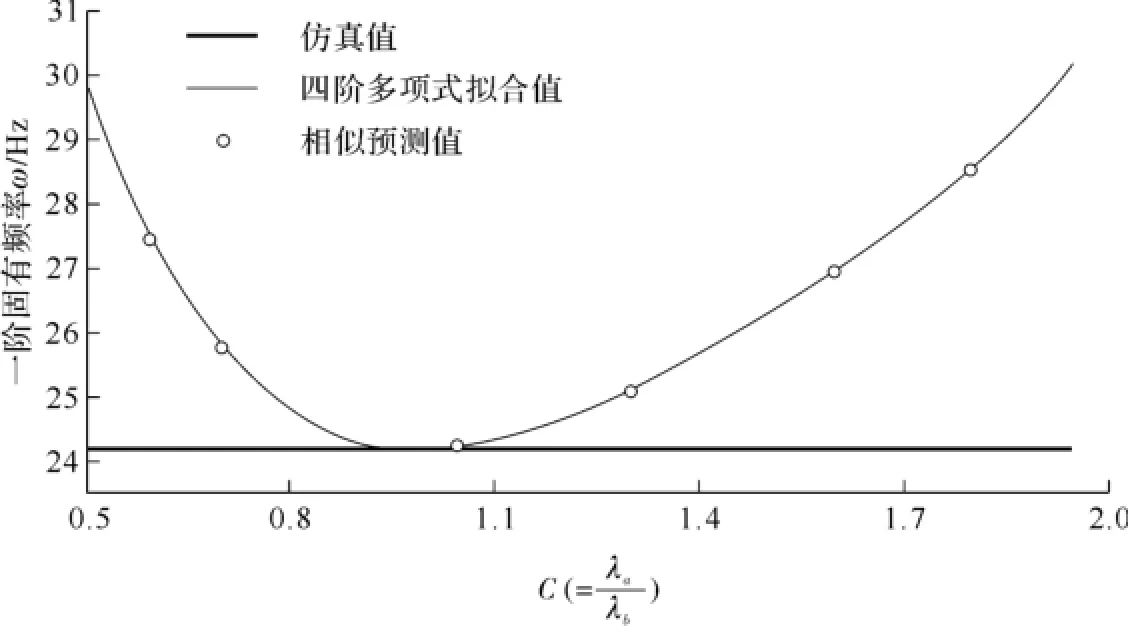
图39 Γ=1.0拟合曲线Fig.39 Fitting curve ofΓ=1.0

图40 Γ=1.1拟合曲线Fig.40 Fitting curve ofΓ=1.1

图41 Γ=1.15拟合曲线Fig.41 Fitting curve ofΓ=1.15
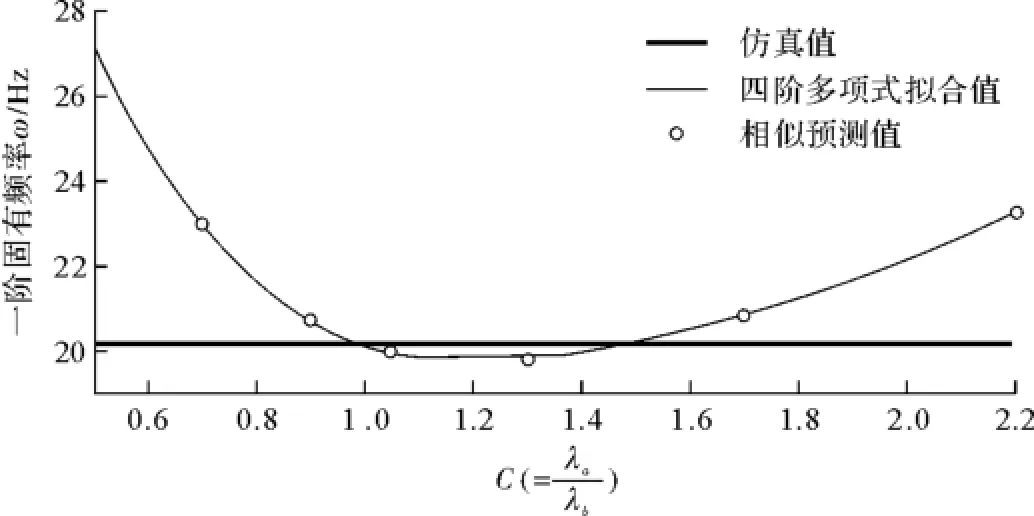
图42 Γ=1.225拟合曲线Fig.42 Fitting curve ofΓ=1.225
由Γ=1.05的边界值和表26得到的结果,可知

对所得区间边界值采用三阶多项式进行插值拟合,得到
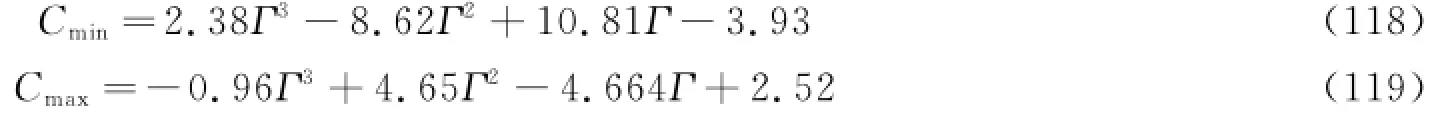
式(118)和式(119)的函数图像见图43。
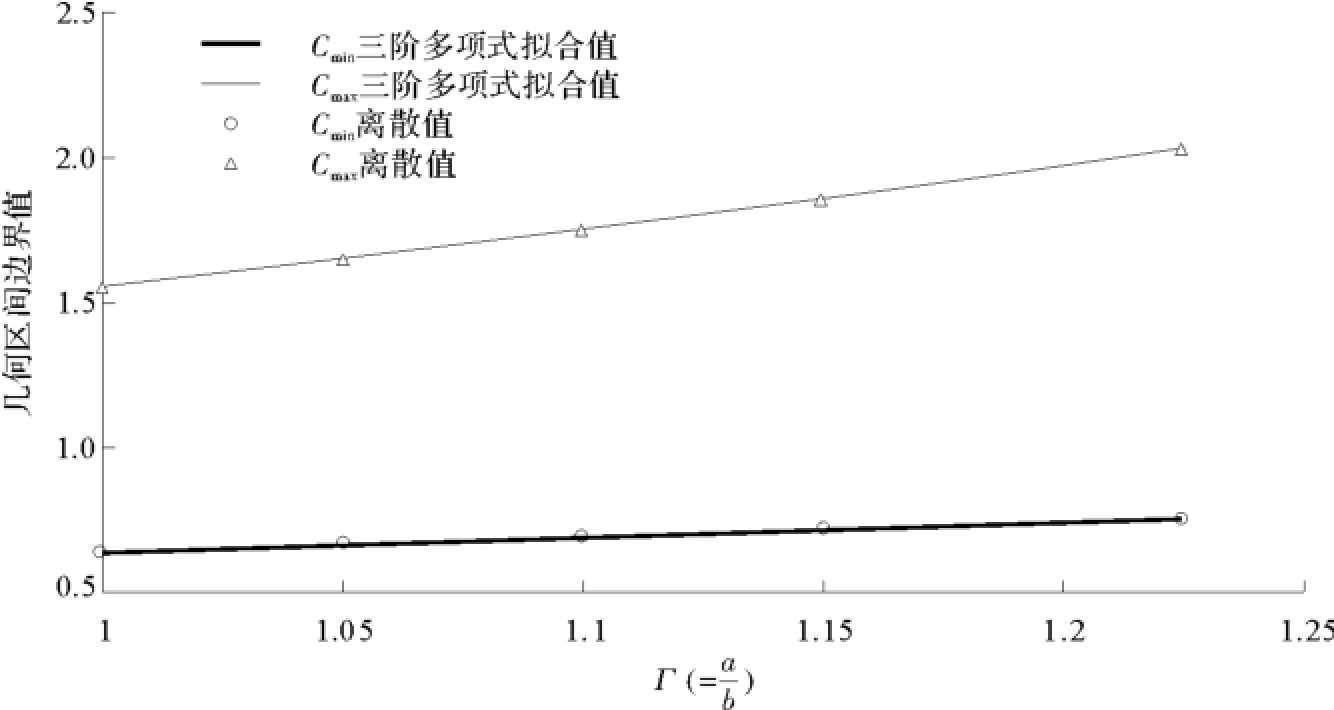
图43 几何适用区间边界值图像Fig.43 Boundary values of applicable geometric interval
图43 中上下两条曲线间的区域即为Γ∈(1,1.225)范围内四边简支弹性薄板一阶固有频率的几何适用区间。
(3)其他阶次固有特性几何区间边界函数确定
由于几何尺寸畸变会导致模型薄板振型跳跃,对于文中所述原型板,使其前j阶具有相同振型的尺寸范围Γ∈(1,Γj],计算得到各阶尺寸范围(见表27)。

表27 各阶尺寸范围Tab.27 Size intervals of each order
由λb=Cλa,任意模型板的长宽比

在满足模型板的高阶固有频率预测值精度的同时,还需要保证模型板与原型板振型相同,则模型尺寸选取应满足以下条件。
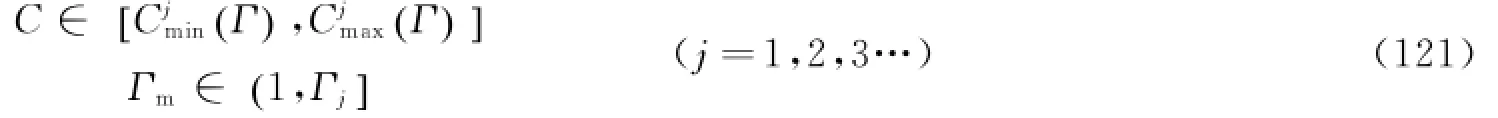
式中,j为固有频率阶数。
由式(120)和式(121)可知,高阶固有频率的畸变模型几何适用区间如下。

根据实际需要,Γ范围在选取时依据的原则不同,得到的各组尺寸范围也有所不同,本文以前8阶振型相同为原则选取振型控制区间,故有Γ8=1.225。
与一阶固有频率不同,弹性薄板高阶固有频率的振型会随着C值的改变而发生变化,其Cjmin(Γ)和Cjmax(Γ)很难用低阶多项式进行拟合,考虑到最终的几何适用区间边界值是由高阶频率预测区间和振型控制区间相交得到的,故在应用数值法进行高阶频率几何区间分析时,所选择的模型板的C值均满足C∈[Γ/Γj,Γ)。根据表28所列原型板参数,求解第5阶固有频率的模型几何适用区间。
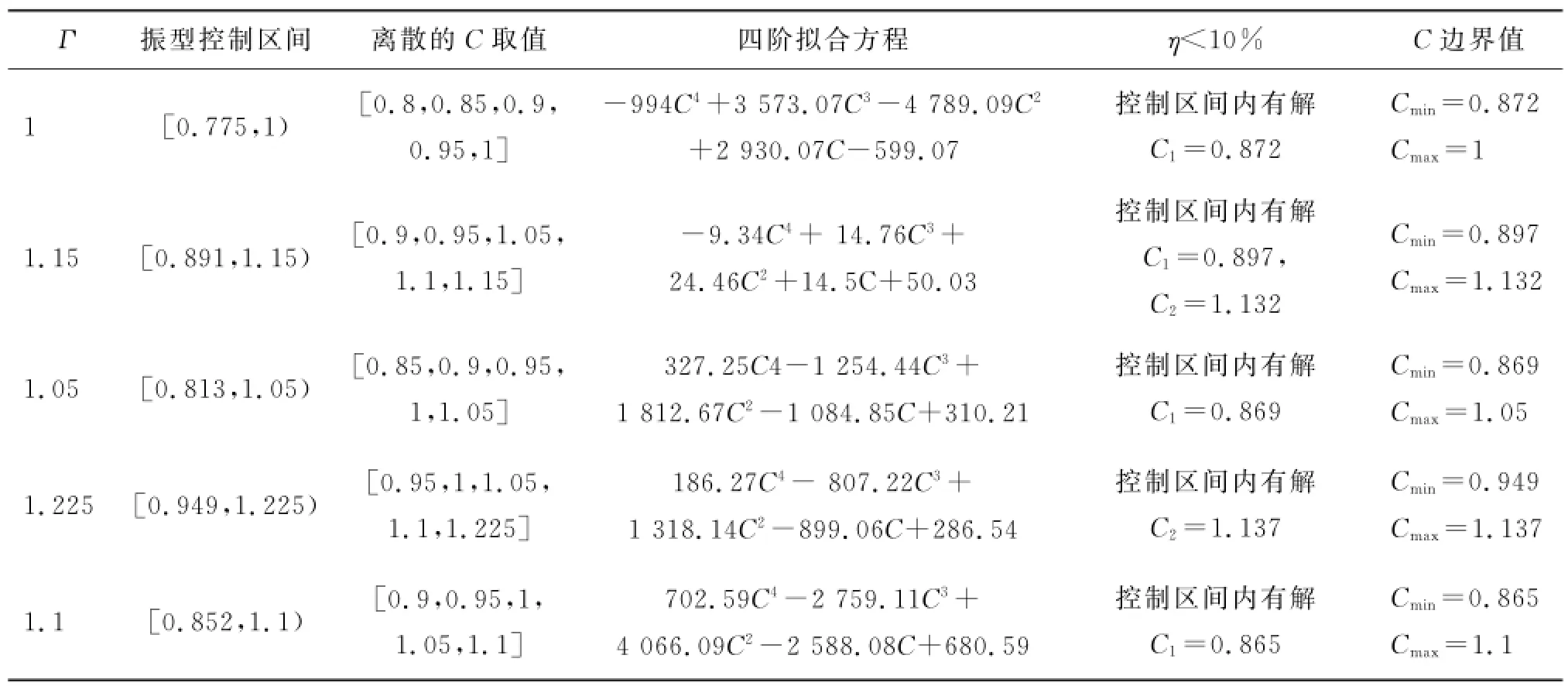
表28 Γ离散点的区间边界值Tab.28 Interval boundary values discreteΓ
整理表28所得数据

对所得区间边界值采用三阶多项式进行插值拟合,得到
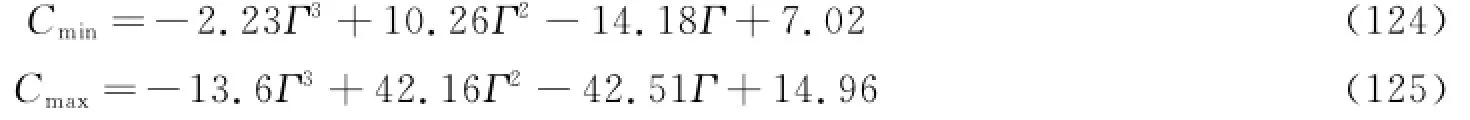
式(124)和式(125)的函数图像见图44。
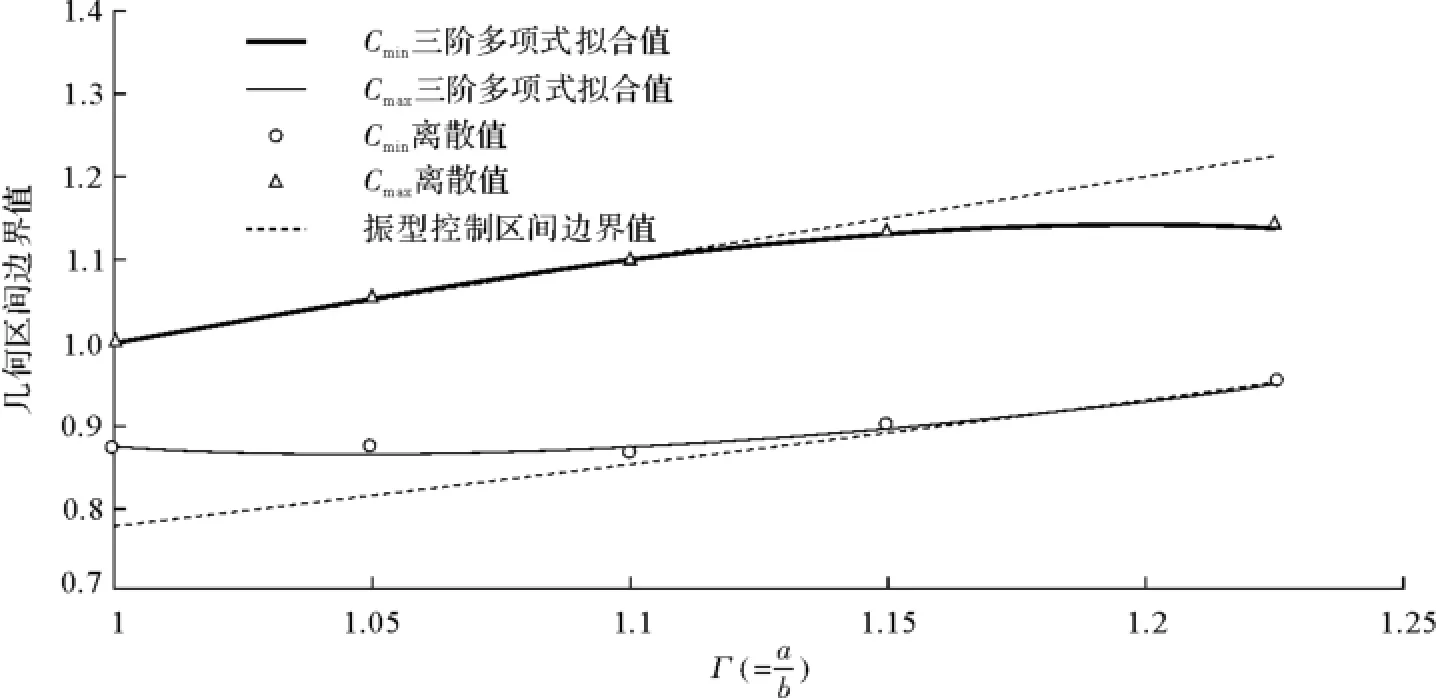
图44 5阶固有频率几何适用区间边界值图像Fig.44 The 5th-order boundary values of applicable geometric intervals
以某一振型下四边简支弹性薄板为例,得到由式(118)和式(119),式(120)和式(121)定义的不同阶次下几何区间边界值Cmin,Cmax。由此可以提出复合材料层合板相似模型几何适用区间的确定方法流程(见图45)。

图45 几何适用区间边界值确定流程Fig.45 Flow chart of determination of applicable geometric intervals
4.4 数值验证和试验验证
4.4.1 完全几何相似关系的数值验证
为了验证相似关系的正确性,通过实例对所得关系式进行验证。所选薄板的原型几何尺寸和材料参数见表29。

表29 薄板原型的几何尺寸和材料参数Tab.29 Size and material parameters of prototype thin plate
对以上弹性薄板原型及模型进行模态分析,计算结果见表30。

表30 弹性薄板各阶模态的固有频率Tab.30 Natural frequencies of elastic thin plate model in each order/Hz
表30结果表明,与根据量纲分析法所得到的比例系数方程求得的Cω的值一致,验证了量纲分析和方程分析所得到的相似关系的正确性。
4.4.2 畸变模型相似关系的试验验证
为了验证理论推导得到的相似关系,根据相似理论的要求,同时模拟加工的局限性,模型均发生畸变,厚度没发生变化。试验采用了不同尺寸的板(见表31)。
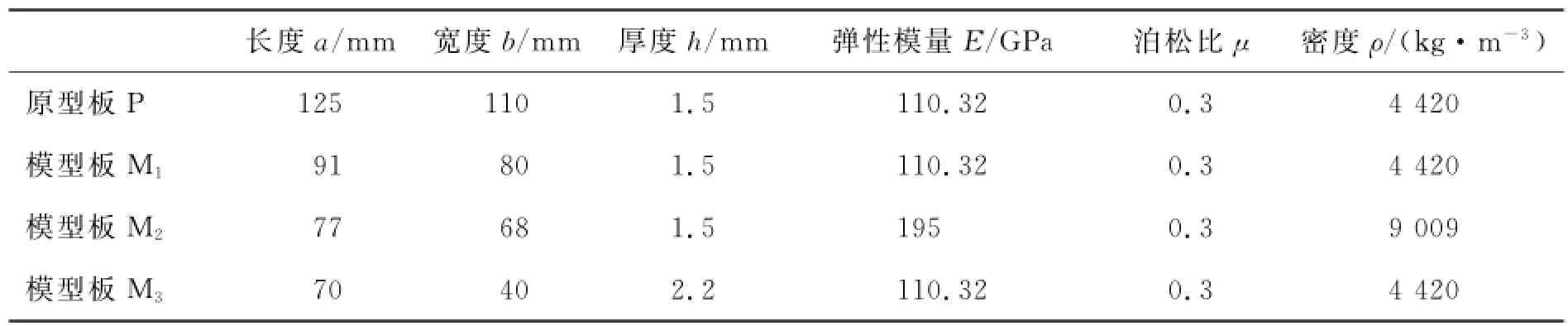
表31 悬臂板的尺寸Tab.31 Size of cantilever thin plate
原型板P、模型板M1和模型板M2的长宽比均为1.13,原型板P、模型板M1和模板M3的材料均为钛合金,模型板M2的材料为625合金(见图46)。

图46 原型板和模型板Fig.46 Prototype and model
(1)厚度或材料畸变 任何物理现象的相似是以完全几何相似为前提的。在模态测试中,表现为模型和原型的固有频率满足确定的缩比关系,同时主振型是完全对应的。鉴于完全几何相似的简单性,笔者仅研究畸变情况下薄板的固有特性的试验预测。由于薄板相对于壳体振动的特殊性,平面内的变形和弯曲变形可以认为互不影响,从而可以在厚度畸变时,通过模型准确预测原型的固有特性。当宽度和长度的某一个或者同时发生畸变时,只有通过预测系数进行畸变的修正。
在经过模态分析后,得到3块悬臂板的固有频率和模态振型(见图47,图48和图49)。虽然在尺寸发生畸变的情况下,振型一般会发生跳跃,但是在试验中,振型是保持对应的。

图47 原型板的主振型Fig.47 Main vibration mode of prototype
图48 模型板M1的主振型Fig.48 Main vibration mode of model M1

图49 模型板M2的主振型Fig.49 Main vibration mode of model M2
表32和表33列出了原型板P、模型板M1和模型板M2的模态振型的固有频率,并对原型板P的频率进行了预测,分析了误差。
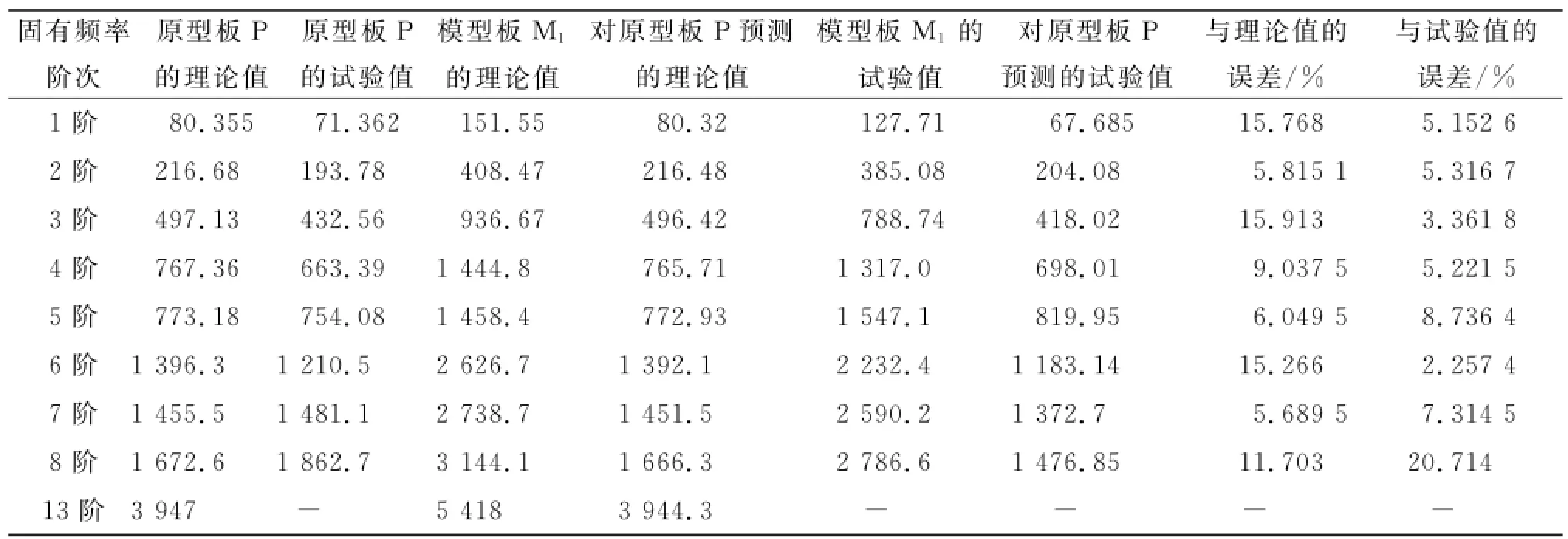
表32 原型板P和模型板M1的对比Tab.32 Comparison of prototype P and model M1

表33 原型板P和模型板M2的对比Tab.33 Comparison of prototype P and model M2
根据以上所得的结果数据,绘制模态相似关系(见图50~图52)。
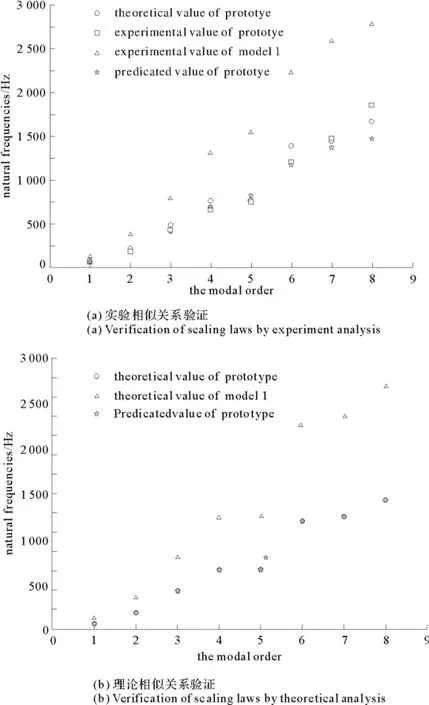
图50 原型板P与模型板M1的模态相似关系Fig.50 Modal similarity relationship between prototype P and model M1

图51 原型板P与模型板M2的模态相似关系Fig.51 Modal similarity relationship between prototype P and model M2
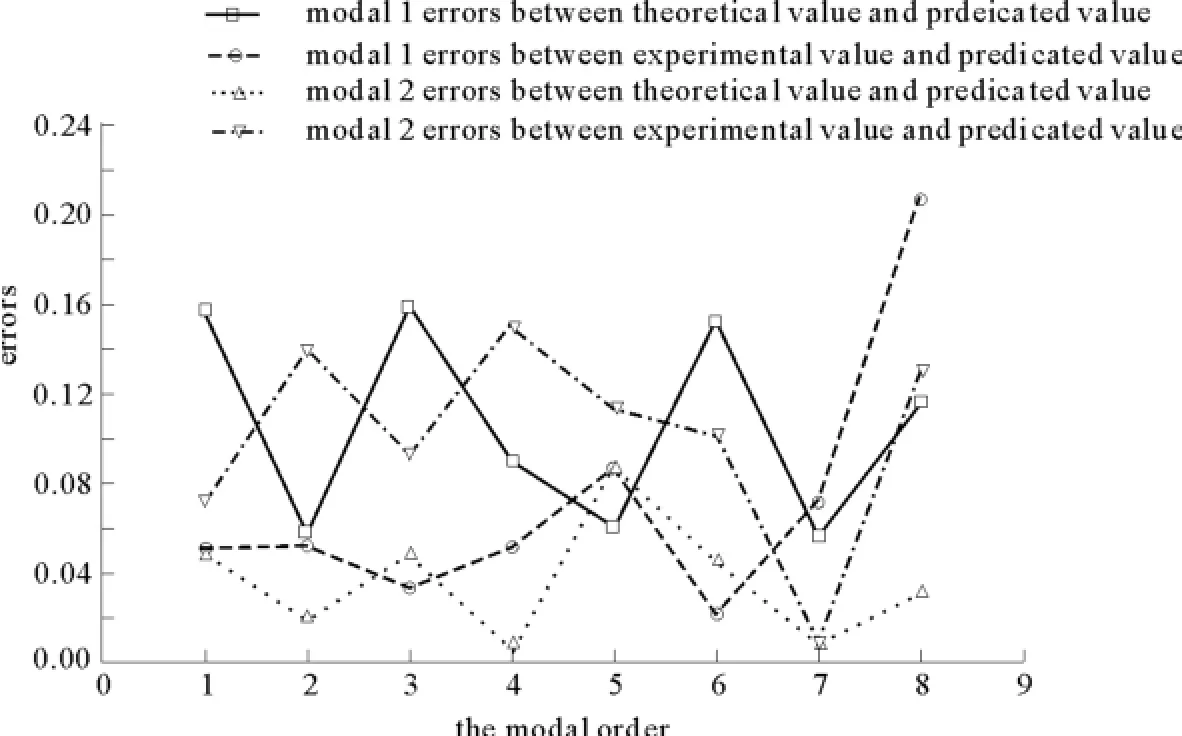
图52 模型板M1与模型板M2的误差Fig.52 Error between model M1and model M2
【数据分析1】 模型M1的理论值通过弯曲振动的缩比关系式预测原型的固有频率,误差较小;模型M2的理论值通过弯曲振动的缩比关系式预测原型的固有频率,误差也很小,说明了理论推导得到的缩比关系式的正确性。虽然理论上的预测误差非常小,但是实验中存在系统误差和偶然误差,甚至过失误差,所以就会出现不可忽略的误差,影响试验的准确性。
【数据分析2】 通过模型M1的试验值预测原型板的固有频率,分别与原型板的试验值与理论值对比,可以发现,在预测理论值方面,误差介于6%~16%之间,比较均匀,在预测试验值方面,前7阶介于1%~10%之间,但是第8阶的误差较大,所以只对低阶的固有频率预测有效;通过模型M2的试验值预测原型板的固有频率,分别与原型板的试验值与理论值对比,可以发现在预测理论值方面,误差介于0%~10%之间,比较均匀,在预测试验值方面,介于0%~15%之间。
【数据分析3】 综合4条误差曲线,模型M1在预测试验值方面误差是最小的,不同阶次的误差差别较大。综合以上分析,模型板M2的材料在预测原型板的固有频率方面比模型板M1的材料更具有优势。
(2)长度或宽度畸变 上述试验对原型板的固有频率的预测是通过缩比关系式直接得出,易于计算,但这只针对厚度或材料发生畸变、模型和原型的长宽比相同的情况下的预测。一但宽度、长度的某一个或者同时发生畸变时,缩比关系[见式(107)]将不再适用。试验件选用表29中的模型板M3,为了实现不同材料时模型对原型的固有频率的预测,以模型板M2作为本试验的原型。
试验测出模型板和原型板的前四阶固有频率后,按图17的流程进行修正,图53和表34表述了修正后的结果,误差均在10%以内,这表明实验结果和畸变修正理论结果一致,即当模型的几何参数发生畸变时,可以采用数值仿真进行畸变修正的方法来对原型的振动进行预测。
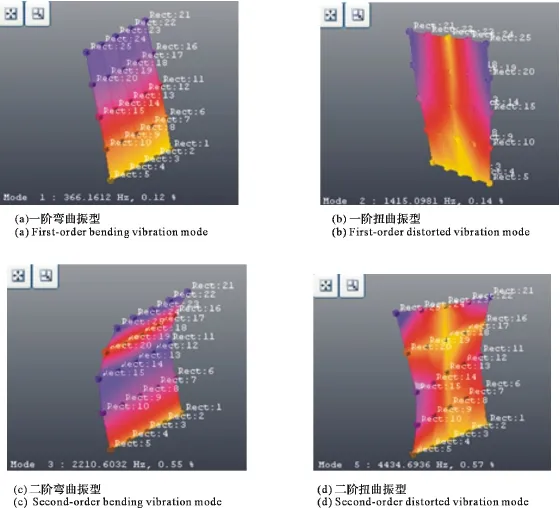
图53 试验中模态主振型Fig.53 Main vibration modal shape during experiment

表34 模型板M3和模型板M2的对比Tab.34 Comparison of model M3and model M2
综合两种不同情况下的试验和不同的试验模型与实验材料对比,得到如下结论。
【结论17】 同种材料之间的模型试验效果要好于异种材料之间的试验结果。
【结论18】 缩比较大的模型的试验结果好于缩比较小的模型的试验结果。
5 结论与展望
5.1 研究内容
本文研究目的是,针对大型高速旋转机械基础单元结构件动力学设计问题,通过创建动力学相似理论,研究其基础单元结构件在完全几何相似和不完全几何相似(即畸变)条件下的动力学相似模型设计及修正方法。
本文研究方法是,以弹性薄板作为大型高速旋转机械典型基础单元结构件,通过平衡方程法和量纲分析法建立弹性薄板结构件完全几何相似的动力学相似关系;针对模型试验中的频率调节问题,讨论附加质量法在相似试验模型频率调节中的应用方法;针对畸变试验模型问题,从畸变产生机理出发,提出一种基于数值拟合的畸变修正理论与方法;基于解析法和统计法,分析薄板构件的结构振动行为敏感性,指导畸变试验模型设计;利用数值分析法确定几何适用区间范围,提出动力学相似设计几何适用区间的确定准则。
围绕上述研究任务,本文完成了以下研究工作。
【研究内容1】 对比国内外相似理论及其在结构振动试验的研究现状,分析基础单元结构件在振动测试试验中涉及的相似设计理论和方法,建立系统级模型结构推算和再现原型结构振动特性和故障特征的方法,以及消除误差的理论基础。
【研究内容2】 针对基础单元结构件动力学相似试验模型的设计,根据相似理论,基于基本力学方程,通过组合量纲分析法、方程分析法和定量分析法,推导相似准则和条件。
【研究内容3】 采用附加集中质量方法研究降低固有频率的相似设计方法,分析不同材料质量块对于薄板模型固有频率的影响。
【研究内容4】 针对相似模型存在的畸变问题,分析畸变产生的原因,提出基于数值拟合的畸变修正方法,通过实例研究进行验证分析。
【研究内容5】 通过材料参数和结构参数等特征参数对于动力学特性的敏感性分析,寻找影响动力学特性的主要特征参数,在忽略次要参数的前提下,对主要参数进行分析、推导、仿真和试验。
【研究内容6】 提出动力学相似模型几何适用区间的确定方法,以四周简支薄板为例,对畸变模型的理论依据进行推导,探讨修正区间问题,并进行相关实验。
5.2 研究结论
通过理论研究、试验验证和科学归纳,笔者得到动力学相似设计的普适流程——“完全相似设计→过渡模型修正→几何适用区间设计→畸变模型→结果修正”,组建起由动力学相似设计概念、动力学相似试验模型设计方法,以及试验模型结果处理方法共同组成的大型高速旋转机械基础单元结构件动力学相似设计的基本理论体系。
根据上述理论研究,得到在大型高速旋转机械基础单元结构件动力学相似设计中,需要遵循的相关科学结论。
【结论1】 动力学相似是指模型和原型在工作状态下,其动力学固有特性、模态振型、动力学响应行为、甚至包括典型故障特征等,在一定范围内一致或成固定比例关系的相似现象。
【Conclusion 1】 Dynamic similitude is the phenomenon that the model and the prototype,under theworking condition,have the same or the fixed proportion dynamic characteristics,vibration shapes, dynamic responses and even typical fault features.
【结论2】 相似模型和原型的本征方程相同,具有相同的模态主振型;对于几何相似的缩比模型和原型,其固有频率与几何缩比成反比;当缩比模型和原型为不同材料时,其固有频率正比于弹性模量和密度的缩比比值的平方根。
【Conclusion 2】 The model and prototype have the same governing equation and the same main vibration shapes.When the scaled model is geometry similitude,the scaling laws of frequencies are the reciprocal of the length scaling law.When the model and prototype have different materials,the frequencies are proportional to the square root of the ratio of Young’s modulus and density.
【结论3】 附加质量块可调整固有频率,也可能使模态次序发生较大变化。加载质量块后,薄板的待测量阶次固有频率将偏离激振力的频段,对相邻各阶固有频率值的影响很小,各阶模态振型将不被改变。
【Conclusion 3】 An additional mass can justify natural frequencies,and change the order of the vibration shape as well.After adding the mass,the natural frequency of the thin plate to be measured would deviate from the excitation frequency range,which has slight effect on the adjacent orders and the vibration model of each order would not change.
【Conclusion 4】 The distortion coefficient of the elastic thin plate isexample indicates that not all distorted models can be corrected,and are applicable intervals in the correction of distorted models.
【结论5】 弹性薄板固有频率对厚度的变化最敏感,随着薄板厚度增加,固有频率将逐渐增大,且随着阶次提高,数值增幅也将增加。
【Conclusion 5】 The natural frequencies of elastic thin plates are the most sensitive to the change of thickness,and as the thickness increases,the frequencies increase.In addition,the increasing amplitude grows as the order increases.
【结论6】 弯曲和扭转振动对长度的敏感性高于对宽度的敏感性,随着这两个参数的增加,固有频率减小,减小幅度将随着阶次增加而逐渐变大。
【Conclusion 6】 The sensitivity to length of both flexural vibrations and torsional vibrations are higher than their sensitivity to width.As these two parameters increase,the natural frequencies decrease, and the decreasing amplitude grows as the order increases.
【结论7】 弦向振动对宽度的敏感性要高于对长度的敏感性;泊松比影响非常小,可以忽略不计,长度和宽度影响较小,但不可被忽略。
【Conclusion 7】 The sensitivity to width of chordwise vibrations are higher than their sensitivity to length.The Poisson’s rate exerts negligible effect.However,though the change of the length and the width has slight effect on the natural frequencies,they cannot be neglected.
【结论8】 弹性薄板振型中某一点的振幅对几何参数的敏感性与其相对位移有关;相对位移越大,敏感性越高;每阶敏感性曲面与其主振型是相同的。
【Conclusion 8】 The geometry sensitivities of each point in the elastic thin plate’s vibration shape are related to their relative displacements.The larger the relative displacements,the higher sensitivities they have.The sensitivity surface is the same to the main vibration shape.
【结论9】 泊松比具有自相似性,弹性模量和密度可以在模型相似关系中得到反映;材料并不是影响振动相似的因素,几何相似是影响动力学相似的条件。
【Conclusion 9】 The Poisson’s rate has the characteristic of self-similitude.The Young’s modulus and the density are reflected in the scaling law.Materials are not the factor to affect the similitude of vibration,but the geometry parameters are.
【结论10】 动力学相似模型几何适用区间与误差控制区间及振型控制区间均相关;振动阶次越高,其几何适用区间范围越小,对于高阶动力学相似模型的参数设计要求更为严格。
【Conclusion 10】 The structure size applicable intervals are related to the vibration shape control intervals and the error range.The higher the vibration order is,the narrow the applicable interval will be, thus it becomes more restrict in the design of high order dynamic similitude test models.
【结论11】 同种材料相似模型试验效果要好于异种材料相似模型的试验结果,缩比较大的模型的试验结果要好于缩比较小的模型的试验结果。
【Conclusion 11】 The predicted results of the test model with the same material to the prototype are better than that with different materials.The predicted results of bigger similitude ratio are better than that of smaller similitude ratio.
5.3 展望
(1)本文仅考虑了以弹性薄板结构件为对象的动力学相似设计研究,对于更复杂的机械系统,还须进行更深入的研究。
(2)本文对于畸变模型的相似关系仅从数值分析角度给出了选择标准,未从理论建模角度给出更可靠的相似关系选择方法;畸变模型动力学相似关系应当从动力平衡方程中推导得到,或从其他更精确的解析方法获取,这将是进一步研究的方向。
(3)本文提出的动力学畸变相似模型均建立于原型与模型同阶振型的基础之上,为工程实践带来很大方便,但同时也限制了畸变模型的适用范围;对于不要求振型一致的场合,应当建立新的研究方法。
(4)本文仅分析了结构和材料参数对于弹性薄板不同振型下固有频率的敏感性,并得到“结论6”~“结论9”;然而在动力学畸变相似模型设计中,各结构和材料参数的独立性,本文没有进行深入讨论,例如,厚度敏感性虽高,但在弹性薄板的固有频率分析中,其与材料参数一样具有很强的独立性,这一点对放宽相似模型厚度尺寸的要求十分重要。
综上所述,关于相似理论在大型高速旋转机械动力学基础结构件试验中的应用研究,笔者认为未来的工作可以从以下3个方面展开。
(1)以大型高速旋转机械基础结构件为研究对象,考虑边界条件、载荷条件、尺寸效应和畸变修正等综合因素下的动力学响应特性模拟和故障特征再现方法,实施由理论研究到工程设计的中间试验应用研究。
(2)动力学相似模型及其输出结果和特征的相似度评价,以及提高相似度的理论与技术研究。在工程应用中,必须解决和回答应用相似理论的可靠度有多大,相似理论对原型特性的预测是否可以达到所要求的精度等问题;必须解决和回答如果可靠度和相似度不满足要求,采用什么理论方法和技术提高等问题。
(3)对于由基础构件组成的大型高速旋转机械复杂系统,其动力学相似试验研究需借助计算机辅助技术,因此,动力学相似物理模型试验和计算机技术的融合技术研究也将是重要的工作之一。
[1]Galilei G,Weston J.Mathematical Discourses Concerning Two new Sciences Relating to Mechanicks and Local Motion:in Four Dialogues.I.of the Resistance of Solids Against Fractions.II.of the Cause of their Coherence.III. of Local Motion,Viz.Equable,and Naturally Accelerate.IV.of Violent Motion,or of Projects.J.Hooke,at the Flower-de-Luce,over-against St.Dunstan's Church in Fleet-Street.,1730.
[2]Harris H G,Sabnis G.Structural Modeling and Experimental Techniques.London:CRC Press,1999.
[3]Jha Anshuman.Dynamic Testing of Structures Using Scale Models[Master Thesis].Montreal,Quebec,Canada: Concordia University,2004.
[4]黄 翀.基于虚拟仪器的大型拖曳水池试验系统的设计与实现[博士学位论文].无锡:江南大学,2009. Huang Chong.Design and Implementation of Towing Tank Test System Based on Virtual Instrument[Ph.D Thesis].Wuxi:Jiangnan University,2009.
[5]Froude W.On the Rolling of Ships.Institution of Naval Architects,1861.
[6]Kelly F C.The Wright brothers:a Biography.DoverPublications.com,1989.
[7]Bertrand J.Démonstration d'un théorème de M.Gauss.Journal de Mathématiques Pures et Appliquées,1848,13(2):80-82.
[8]Stull R B.Similarity Theory.Berlin:Springer Netherlands,1988.
[9]Bertrand J.Réponsea la note de M.Helmholtz.CR Acad.Sci.Paris,1868,67(3):773-775.
[10]Buckinghan E.On Physically Similar Systems,Illustrations of the Use of Dimensional Equations.Physical Review, 1914,4(4):345-376.
[11]Kirpichev M V,Gukhman A A.Application of Similarity Theory of the Experiment.Trudy Leningr.Obl NIl Teplotekhn.In-ta,1931,1(1):11-23.
[12]Dieterich J Schuring.Scale Models in Engineering Fundamental and Applications.Oxford:Pergamon Press,1977.
[13]Birkhoff G.Mathematics for Engineers—III:Dimensional Analysis of Partial Differential Equations.Electrical Engineering,1948,67(12):1185-1188.
[14]Vaschy A.Théorie de l'électricité:Exposédes Phénomènesélectriques et Magnétiques FondéUniquement sur l' expérience et le Raisonnement.Librairie Polytechnique,Baudry et Cie,1896.
[15]Rayleigh L.The Principle of Similitude.Nature,1915,95(66):591.
[16]Reynolds O.An Experimental Investigation of the Circumstances which Determine Whether the Motion of Water Shall be Direct or Sinuous,and of the Law of Resistance in Parallel Channels.Proceedings of the Royal Society of London,1883,35(224-226):84-99.
[17]Goodier J N,Thomson W T.Applicability of Similarity of Principles to Structural Models.NACA Tech. Note993,1944.
[18]Goodier J N.Dimensional Analysis(First Edition).New York:John Wiley&Sons,1950:1035-1045.
[19]Langhaar H L.Dimensionless Analysis and Theory of Models(First Edition).New York:John Wiley&Sons,1951. [20]Pankhust R C.Dimensional Analysis and Scale Factors(First Edition).London:Chapman&Hall,1964.
[21]Macagno E O.Historico-Critical Review of Dimensional Analysis.Journal of the Franklin Institute,1971,292(6): 391-402.
[22]Szues E.Similitude and Modeling.Mathematics and Computers in Simulation,1980,22(4):382.
[23]David F W,Butterworths N H.Experimental Modeling in Engineering.Journal of Mechanical Working Technology, 1983,8(4):374-375.
[24]列兹尼亚科夫A B,著,王成斌,译.相似方法(第一版).北京:科学出版社,1964.
[25]谈庆明.量纲分析.合肥:中国科学技术大学出版社,2005. Tan Qingming.Dimensional Analysis.Hefei:China University of Science and Technology Press,2005.
[26]杨俊杰.相似理论与结构模型试验.武汉:武汉理工大学出版社,2005. Yang Junjie.The Similarity Theory and Structural Model Test.Wuhan:Wuhan University of Technology Press,2005.
[27]徐 挺.相似理论与模拟实验(第一版).北京:中国农业机械出版社,1982. Xu Ting.The Similarity Theory and Simulation Experiments(First Edition).Beijing:China Agriculture Machinery Press,1982.
[28]周美立.相似工程学.北京:机械工业出版社,1998. Zhou Meili.Similar Engineering.Beijing:Machinery Industry Press,1998.
[29]Kiine SJ.Similitude and Approximation Theory(First Edition).New York:McGraW-Hill,1965.
[30]Szücs E.Fundamental Studies in Engineering(II),Similitude and Modeling.Elsevier Scientific Publishing Co, Amsterdam,Netherlands,1980:138.
[31]Qian Y,Swanson SR,Nuismer RJ,et al.An Experimental Study of Scaling Rules for Impact Damage in Fiber Composites.Journal of Composite Material,1990,24(5):559-570.
[32]Qian Y,Swanson S R.Experimental Measurement of Impact Response in Carbon/Epoxy Plates.AIAA Journal, 1990,28(6):1069-1074.
[33]Morton J.Scaling of Impact-Loaded Carbon-Fiber Composites.AIAA Journal,1988,26(8):989-994.
[34]Singhatanadgid P,Ungbhakornt V.Scaling Laws for Vibration Response of Anti-Symmetrically Laminated Plates. Structural Engineering and Mechanics,2002,14(3):345-364.
[35]Ungbhakorn V,Singhatanadgid P.Similitude Invariants and Scaling Laws for Buckling Experiments on Anti-Symmetrically Laminated Plates Subjected to Biaxial Loading.Composite Structure,2003,59(4):455-465.
[36]Jha A,Sedaghati R,Bhat R.Dynamic Testing of Structures Using Scale Models//Proceedings of the 46th AIAA/ ASME/ASCE/AHS/ASC Structures,Structural Dynamics and Materials Conference,Austin,Texas,2005:85-100.
[37]Songkhla A N,Singhatanadgid P.Accuracy of the Scaling Law for Experimental Natural Frequencies of Rectangular thin Plates//The 19th Conference of Mechanical Engineering Network of Thailand,Thailand,2005:19-21.
[38]Ungbhakorn V,Singhatanadgid P.Similitude and Physical Modeling for Buckling and Vibration of Symmetric Cross-Ply Laminated Circular Cylindrical Shells.Journal of Composite Materials,2003,37(19):1697-1712.
[39]Ungbhakorn V,Wattanasakulpong N.Structural Similitude and Scaling Laws of Anti-symmetric Cross-Ply Laminated Cylindrical Shells for Buckling and Vibration Experiments.International Journal of Structural Stability and Dynamics, 2007,7(4):609-627.
[40]Kee Y J,Kim J H.Vibration Characteristics of Initially Twisted Rotating Shell Type Composite Blades.Composite Structures,2004,64(2):151-159.
[41]Torkamani S,Navazi H M,Jafari A A,et al.Structural Similitude in free Vibration of Orthogonally Stiffened Cylindrical Shells.Thin-Walled Structures,2009,47(11):1316-1330.
[42]Bijan D,Suong H,Mehdi H.Similitude Study on Bending Stiffness and Behavior of Composite Tubes.Journal of Composite Materials,2012,46(21):2695-2710.
[43]Murugan R,Prabhu R V,Thyla P R.Establishment of Structural Similitude for Elastic Models and Validation of Scaling Laws.Ksce Journal of Civil Engineering,2013,17(1):139-144.
[44]Krayterman B,Gajanan M,Sabnis M,et al.Similitude Theory:Plates and Shells Analysis.Journal of Engineering Mechanics,1984,110(9):1247-1263.
[45]Simitses GJ,Rezaeepazhand J.Structural Similitude and Scaling Laws for Laminated Beam-Plates.American Society of Mechanical Engineers,Aerospace Division AD,1992,26(1):37-45.
[46]Rezaeepazhand J,Simitses G J,Starnes J H.Use of Scaled-down Models for Predicting Vibration Response of Laminated Plates.Composite Structure,1995,30(4):419-426.
[47]Simitses G J,Starnes J H,Rezaeepazhand J.Structural Similitude and Scaling Laws for Plates and Shells:a Review//AIAA/ASME/ASCE/AHS/ASC 41st Structures,Structural Dynamics,and Materials Conference and Exhibit,2000,1(1-3):393-403.
[48]Rezaeepazhand J,Wisnom M R.Scaled Models for Predicting Buckling of Delaminated Orthotropic Beam-Plates. Composite Structure,2009,90(1):87-91.
[49]Rezaeepazhand J,Simitses G J,Starnes J H.Scale Models for Laminated Cylindrical Shells Subjected to Axial Compression.Composite Structure,1996,34(4):371-379.
[50]Rezaeepazhand J,Simitses G J,Starnes J H.Design of Scaled down Models for Predicting Phell Vibration Response. Journal of Sound and Vibration,1996,195(2):301-311.
[51]Rezaeepazhand J,Simitses G J.Structural Similitude for Vibration Response of Laminated Cylindrical Shells with Double Curvature.Composites(Part B-Engineering),1997,28(3):195-200.
[52]Simitses G J.Structural Similitude for Flat Laminated Surfaces.Composite Sturctures,2001,51(2):191-194.
[53]Soedel W.Similitude Approximations for Vibrating Thin Shells.The Journal of the Acoustical Society of America, 1971,49(5):1535-1541.
[54]Chouchaoui C S,Parks P,Ochoa O O.Similitude Study for a Laminated Cylindrical Tube under Tension,Torsion, Bending,Internal and External Pressure(Part II):Scale Models.Composite Structures,1999,44(4):231-236.
[55]Wu J J,Cartmell M P,Whittaker A R.Prediction of the Vibration Characteristics of a full-Size Structure from those of a Scale Model.Computers and Structures,2002,80:1461-1472.
[56]Wu J J.Dynamic Analysis of a Rectangular Plate under a Moving Line Load Using Scale Beams and Scaling Laws. Computers and Structures,2005,83(19):1646-1658.
[57]Wu J J.Prediction of the Dynamic Characteristics of an Elastically Supported full-Size Fat Plate from those of its Complete Similitude Scale Model.Computers and Structures,2006,84:102-114.
[58]Wu J J.Prediction of Lateral Vibration Characteristics of a full-Size Rotor-Bearing System by Using those of its Scale Models.Finite Elements in Analysis and Design,2007,43(10):803-816.
[59]Young Y L.Dynamic Hydroelastic Scaling of self-Adaptive Composite Marine Rotors.Composite Structures,2010, 92(1):97-106.
[60]林 皋,朱 彤,林 蓓.结构动力模型试验的相似技巧.大连理工大学学报,2000,40(1):1-8. Lin Gao,Zhu Tong,Lin Bei.Similarity Technique for Dynamic Structural Model Test.Journal of Dalian University of Technology,2000,40(1):1-8.
[61]迟世春,林少书.结构动力模型试验相似理论及其验证.世界地震工程,2004,20(4):11-20. Chi Shichun,Lam Siushu.Validation of Similitude Laws for Dynamic Structural Model Test.World Information on Earthquake Engineering,2004,20(4):11-20.
[62]雷正保,钟志华.动态大位移大转角大变形弹塑性相似结构的相似比.机械工程学报,1999,35(2):6-9. Lei Zhengbao,Zhong Zhihua.Similitude Ratios of Elastic Plastic Similitude Structure with Large Displacements and Large Deformations for Dynamic System.Chinese Journal of Mechanical Engineering,1999,35(2):6-9.
[63]雷正保,刘振闻,钟志华.相似结构动力响应的外推方法及精密特性.振动与冲击,1999,18(2):17-22. Lei Zhengbao,Liu Zhenwen,Zhong Zhihua.Extrapolation of Dynamic Response Resulting from Fem and it’s Accuracy for Structure with Elastic Plastic Materials and Large Displacements&Deformations.Journal of Vibration and Shock,1999,18(2):17-22.
[64]李少华,杨智春,谷迎松.一种复合材料跨声速颤振模型的部分结构相似设计方法.机械强度,2009,31(2): 339-343. Li Shaohua,Yang Zhichun,Gu Yingsong.Partial Structure Similarity Method to Design Composite Transonic Flutter Model.Journal of Mechanical Strength,2009,31(2):339-343.
[65]胡培民.转子扭转振动的相似模型试验分析.机械科学与技术,1997,16(6):1084-1087. Hu Peimin.Analysis of Similarity Model Testing for Torsional Vibration of Rotor.Mechanical Science and Technology,1997,16(6):1084-1087.
[66]刘尔重.相似定理在复合材料结构件上的应用.航空发动机,1999,2(2):50-53. Liu Erzhong.The Application of Similarity Theorem in Composite Material Structures.Aeroengine,1999,2(2): 50-53.
[67]晏砺堂,王德友.航空双转子发动机动静件碰摩振动特征研究.航空动力学报,1998,13(2):173-221. Yan Litang,Wang Deyou.Vibration Features from Rubbing Between Rotor and Casing for a Dual-Shaft Aeroengine.Journal of Aerospace Power,1998,13(2):173-221.
[68]王德友.发动机转静件碰摩振动特征的提取与理论研究[博士学位论文].北京:北京航空航天大学,1995. Wang Deyou.Extraction and theory research of Vibration Features from Rubbing Between Rotor and Casing[Ph.D Thesis].Beijing:Beijing University of Aeronautics and Astronautics,1995.
[69]郝燕平.叶轮机叶片结构相似性问题的理论研究//中国航空学会第六届动力年会论文集,南京,2006:CSAA06-P-084. Hao Yanping.Theoretical study of similar problems in turbomachine blade structure//China Aviation Society Sixth Dynamic Annual Meeting Proceedings,Nanjing,2006:CSAA06-P-084.
[70]Higgins T J.Electroanalogic Methods.Applied Mechanics Reviews,1957,10(8):331-335.
[71]沈自求.相似理论中若干问题的讨论.科学通报,1962(8):29-35. Shen Ziqiu.The Discussion on Several Problems of Similarity Theory.Chinese Science Bulletin,1962(8):29-35.
[72]夏晓东.土壤–机械系统的系列畸变模型实验技术研究.农业机械学报,1983(4):10-26. Xia Xiaodong.Study of Test Technique of A Series of Distorted Model of Soil Machine Systems.Transactions of the Chinese Society for Agricultural Machinery,1983(4):10-26.
[73]Gukhman A A.Introduction to the Theory of Similarity.New York:Academic Press,1965:185-235.
[74]吴家龙.弹性力学.北京:高等教育出版社,2001:317-343. Wu Jialong.Elasticity.Beijing:Higher Education Press,2001:317-343.
[75]徐芝纶.弹性力学(下).北京:科学出版社,1988:1-12. Xu Zhilun.Elasticity(II).Beijing:Science Press,1988:1-12.
[76]韩清凯,孙 伟.弹性力学及有限元法基础教程.沈阳:东北大学出版社,2009. Han Qingkai,Sun Wei.A First Course in Elasticity Theory and Finite Element Method.Shenyang:Northeastern U-niversity Press,2009.
[77]李明强.直升机机体动力学相似模型设计与结构响应主动控制[博士学位论文].南京:南京航空航天大学,2008. Li Mingqiang,Dynamic Design and Active Control of Structural Response of Helicopter Airframe Analogous Model[Ph.D Thesis].Nanjing:Nanjing University of Aeronautics and Astronautics,2008.
[78]Cremer L,Heckl M,Petersson B A T.Structure-Borne Sound:Structural Vibrations and Sound Radiation at Audio Frequencies.Berlin,Germany:Springer,2005.
[79]向建华,廖日东,蒲大宇.带集中质量块薄板的移频数值仿真.西安交通大学学报,2010,44(11):82-86. Xiang Jianhua,Liao Ridong,Pu Dayu.Numerical Simulation on Frequency Shift of Thin Plate with Lumped Mass Block.Journal of Xi’an Jiaotong University,2010,44(11):82-86.
[80]Amabili M,Carra S.Experiments and Simulations for large-Amplitude Vibrations of Rectangular Plates Carrying Concentrated Masses.Journal of Sound and Vibration,2012,331(1):155-166.
[81]Boay C G.Free Vibration of Rectangular Isotropic Plates with and without a Concentrated Mass.Computers& Structures,1993,48(3):529-533.
[82]Rosa S D,Franco F,Capasso D,et al.The Effect of Concentrated Masses on the Response of a Plate under a Turbulent Boundary Layer Excitation.Mechanical Systems and Signal Processing,2011,25(4):1192-1203.
[83]罗 忠,张海军,张 凯,等.基于集中质量块法的叶片试验模型的模态调节方法.东北大学学报(自然科学版), 2012,33(10):1319-1321. Luo Zhong,Zhang Haijun,Zhang Kai,et al.Modal Adjustment Method Based on Lumped Mass for Test Model of Blade.Journal of Northeastern University(Natural Science),2012,33(10):1319-1321.
[84]许本文,焦群英.机械振动与模态分析基础.北京:机械工业出版社,1998. Xu Benwen,Jiao Qunying.Fundamentals of Mechanical Vibation and Modal Analysis.Beijing:China Machine Press,1998.
[85]Lee I W,Kim D O.Natural Frequency and Mode Shape Sensitivities of Damped Systems(Part1):Distinct Natural Frequencies.Journal of Sound and Vibration,1999,223(3):399-412.
[86]Lee I W,Jung G H.An Efficient Algebraic Method for Computation of Natural Frequency and Mode Shape Sensitivities(Part I):Distinct Natural Frequencies.Computers and Structures,1997,629(3):429-435.
[87]Luo Z,Han Q K,Qin G M,et al.Dynamic Similarity Analysis on Scaled-down Model of a thin Plate with Concentrated Mass//14th Asia Pacific Vibration Conference,Hong Kong,2011:623-630.
[88]Lee I W,Jung G H.An Efficient Algebraic Method for Computation of Natural Frequency and Mode Shape Sensitivities(PartⅡ):Multiple Natural Frequencies.Computers and Structures,1997,62(3):437-443.
[89]杨大彬,张毅刚,吴金志.基于ANSYS的灵敏度分析及其在单层网壳中的应用.世界地震工程,2009,25(4):87-91. Yang Dabin,Zhang Yigang,Wu Jinzhi.Sensitivity Analysis based on ANSYS and Its Application to Single-Layer Reticulated Shell.World Earthquake Engineering,2009,25(4):87-91.
[90]Kurt Binder,Heermann Dieter W.Monte Carlo Simulation in Statistical Physics-an Introduction.Berlin/ Heidelberg:Springer,1997.
[91]Fang K T,Wang Y.Number Theoretic Methods in Statistics.New York:Chapman and Hall,1994.
[92]Myers R H,Anderson-Cook C M.Response Surface Methodology:Process and Product Optimization Using Designed Experiments.Wiley.com,2009.
* 中国国家重点基础研究发展计划(973计划)项目《高端压缩机组高效可靠及智能化基础研究》(No.2012CB026000),中国国家自然科学基金资助项目《旋转结构件模型试验的动力学相似理论及其应用研究》(No.51105064),中央高校基本科研业务费资助教育部新世纪优秀人才培育项目《混合式复杂转子系统动力学相似试验模型的设计方法研究》(No.N1305030011)
- 数字制造科学的其它文章
- Основытеориипроэктированияосновныхэлементовструктуры динамическианалогичныхконструкцийдлякрупногабаритных высокоскоростныхвращающихсямеханизмов*
- 動力学相似理論に基づく大型高速回転機械基礎構造部品の設計に関する基礎理論*
- Die Grundlagetheorieüber das DynamikÄhnlichkeitsdesign von den Strukturkomponenten der Grundlageeinheit der großen Hochrotationsmaschinen*
- Théorie de base de la conception dynamique similaire pour les composants de base structurelle de grandes machines tournantàhaut débit*
- Basic Theory of Dynamically Similar Design for Basic Structural Components of Large High-Speed Rotating Machinery*

