固体火箭的鲁棒自适应耗尽关机制导方法研究

周 军 潘彦鹏 呼卫军

西北工业大学精确制导与控制研究所，西安 710072

取消推力终止装置的固体火箭以其易于生产、储存、运输、维护和快速发射等显著优势成为发展趋势，但这给制导带来了新难题——耗尽关机制导问题，即在推力、秒耗和关机时间随机摄动情况下，如何导引才能使能量随机耗尽时火箭的弹道参数正好满足射程和射向要求。显然，新问题给导引方法的鲁棒与自适应能力提出了更高要求。

目前对耗尽关机制导问题的研究，以文献[1]提出的方法最为经典和最具影响力，该方法以视速度模量为控制变量，通过闭路导引段、姿态调制段和常姿态导引段的分段逐步导引实现待增速度快速收敛和能量耗散管理，以达到关机点待增速度趋于零的导引目的。文献[2-3]在文献[1]的成果基础上进行了改进研究，前者通过耗尽关机时间的预估与补偿提高制导精度，后者通过改进能量耗散模型, 提高了远程火箭对远、中、近程飞行任务的适应性。文献[4]采用与文献[1]相似的能量管理原理，研究了有限推力下轨道转移中耗尽关机制导问题。但上述文献中导引方法的精度严重依赖于： 1)能量管理方法的精度； 2)是否进行关机时间补偿及补偿精度。这是因为耗尽关机的能量管理是个强非线性矢量控制问题(文献中作了近似或线化处理)，必然影响待增速度的控制精度，对于3000km的弹道，当待增速度控制精度大于5m/s时，落点偏差将达5km以上。此外，固体火箭的耗尽关机时间随机摄动，误差可达2～3s以上，由此引起的入轨/落点偏差从几公里到几百公里都有可能，由补偿精度不高引起的入轨/落点散布也能达到数公里级。因而文献中方法的鲁棒性和自适应性不强，进一步提高制导精度的能力非常有限。

本文针对上述耗尽关机制导方法的不足，基于闭路制导和零射程线理论的结合应用，提出了一种不需预估及补偿关机时间且耗能管理更精确的自适应耗尽关机制导方法，该方法首先利用闭路制导方法，进行待增速度Vg的快速收敛控制。当Vg收敛至理想值时，采用基于零射程线的能量管理方法将箭体导引至零射程线能量耗散运动状态，并通过Vg反馈实时修正零射程线，实现在每个零射程线导引周期上使Vg→0的导引控制目的。由于零射程线运动状态具有速度冲量对轨迹终端位置不敏感的特性，因此无需进行关机时间预估和补偿，又因为采用了Vg反馈修正，保证了能耗管理有足够的精度。

因此，本文方法对推力、秒耗和关机时间的随机摄动有足够的鲁棒与自适应能力，且具有精度高和易于工程实现的特点。

1 经典导引方案

经典耗尽关机导引方法以文献[1]为代表，由闭路导引段、姿态调制段和常姿态导引段3部分构成，以纵向通道为例，导引剖面示意图如图1。

图1 经典导引方案示意图

2 与经典导引方案的对比分析

与经典方法不同，本文在能量管理段采用基于零射程线的能量耗散导引方法，在闭路导引段和能量管理导引段之间加入过渡导入段。同时为提高关机点速度矢量的导引精度，将末速精调段由基于待增速度反馈调节导引和预关机状态导引两部分组成，待增速度反馈调节导引通过在零射程线附近的机动飞行实现Vg→0的收敛导引，使箭体在关机前进入预关机状态，该状态具有速度冲量变化不会引起轨迹终点位置变化的特性，因此只要保证预关机状态导引段飞行时间大于关机摄动时间，就可避免关机时间预估与补偿的问题。射面内导引方案的示意图如图2所示。

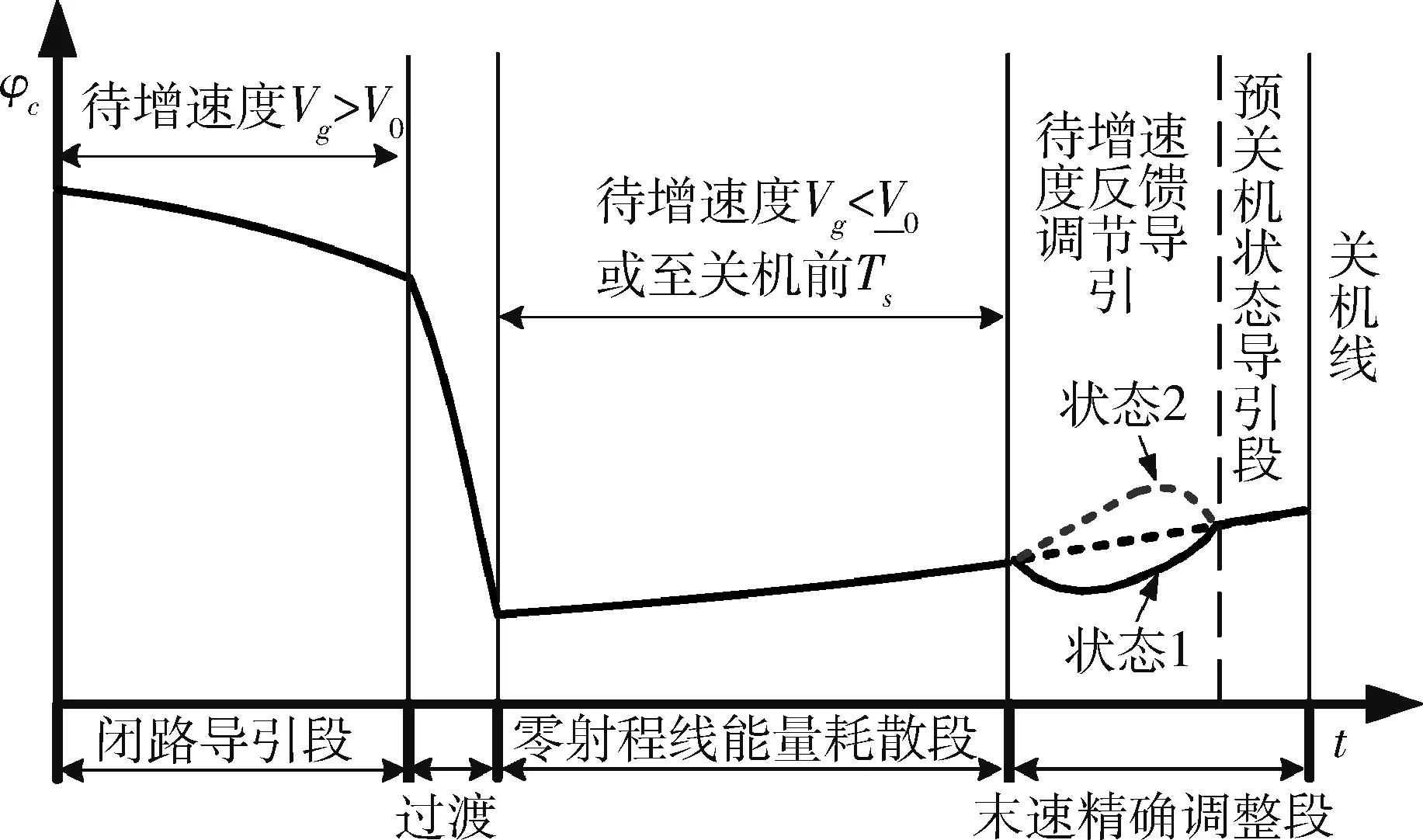
图2 本文导引方案示意图

3 闭路导引段制导律设计

3.1 考虑地球旋转的需要速度计算

在中心引力场假设下，火箭的自由飞行轨迹为图3所示的椭圆轨道。

图3 自由飞行椭圆弹道几何关系

根据椭圆几何性质，其长半轴a为：

(1)

同时，椭圆轨迹上任一点的速度满足：

(2)

联立式(1)和(2)，可得当前位置的需要速度大小为：

(3)

确定a和VR后，从r到rt的自由飞行时间为：

(4)

若火箭目标点随地球转动，则目标点经纬度(λT,BT)与飞行时间有如下关系：

(5)

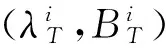
图4 需要速度和自由飞行时间迭代流程

3.2 推力方向调整策略

推力方向调整策略即箭体姿态角的确定策略，推力方向调整的目的是使待增速度Vg尽快收敛，这里选择推力方向与待增速度方向相同的策略计算箭体俯仰角φ和偏航角ψ，公式如下：

(6)

3.3 弹道修正策略

上述闭路导引计算是在中心引力场假设下得到的，没有考虑地球扁率对轨迹终点精度的影响，本文采用文献[5]的方法得到地球扁率产生的终点偏差Be，λe，并将其引入式(5)进行实时修正。

4 零射程线能耗段制导律设计

当箭体在惯性弹道射面内运动时，其射程角βL满足如下公式：

(7)

式中VxA，VyA为速度在当地射面坐标系kxAyAzA中的分量(定义同发射系)。依据零射程线的定义，有：

(8)

从而可到射面内零射程线与kxA轴的夹角γ0为：

(9)

将式(8)整理后带入式(9)，并且与式(7)分别求VxA，VyA偏导数的结果联立得到：

(10)

其中c=rt/r。因此零射程线的方向矢量在当地射面坐标系下可表示为：

(11)

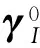
(12)

该段的侧向采用闭路导引，当侧向待增速度Vgz收敛到足够小时，侧向单独切入末速调整导引段。纵向末速调整导引段的切入条件依据Vg及剩余飞行时间而定，只要保证发动机关机时间时偏限情况下能进入预关机状态即可。

5 过渡段与末速精调段制导律设计

5.1 过渡段导引律

过渡段导引实现闭路段到零射程线能耗管理段的过渡导引，并保证进入零射程线能耗导引段时满足Vg→0的要求，这对过渡导引段的切入条件提出了严格要求，本文采用预测算法解决从闭路段到过渡段的切换条件问题，通过预测过渡段的速度增量，确定切入过渡段时Vg的预留量，从而保证了进入能耗段时Vg能够足够小(具体值依据制导精度定)。

假设过渡段采用等角速率ωm下翻，初值为φ1(t0)，终值为φ2(t2)，显然有：

φ2=φ1+ωmtΔ

(13)

式中tΔ为过渡段飞行时间，则过渡段速度增量ΔW可用下式进行预估：

(14)

式中aW为视加速度矢量，g为引力加速度矢量。应用式(14)推演，得预估算法如下：

ΔWx=A1xsinωm(t0+tΔ)+A2xcosωm(t0+tΔ)+

A12x+Bx

ΔWy=A1ysinωm(t0+tΔ)-A2ycosωm(t0+tΔ)+

A12y+By

ΔWz=A1zsinωm(t0+tΔ)+A2zcosωm(t0+tΔ)+

A12z+Bz

(15)

式中

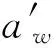
A12y=A2ycosωmt0-A1ysinωmt0，By=gytΔ

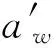
A12z=-A1zsinωmt0-A2zcosωmt0，Bz=gztΔ

其中ψ1为t0时刻的偏航角。

在闭路后段采用式(15)预估ΔW，当满足

ΔW≅Vg

(16)

时，切入过渡导引段。

在整个过渡导引段，偏航仍采用闭路导引。

5.2 末速精调段导引律

由于过渡段预估算法近似及能耗段导引偏差的存在，难以保证关机点Vg总能满足精度要求，因此在关机前需要进行末速精确调整导引，从而使关机点Vg一定收敛至足够小。该导引段由待增速度反馈调节导引和预关机导引两段组成。

待增速度反馈调节导引利用待增速度调整推力方向，通过关机前的小幅机动进行能量精确管理，实现末速的精确控制，其基本导引律方程如下：

φ=φγ0(t)+k1Vgx+k2Vgy

ψ=ψ(t)+k3Vgz

(17)

其中k1～k3为反馈条件系数。

当待增速度满足Vg<ε(ε视制导精度要求)时，进入预关机状态导引段，此时|k1Vgx|，|k2Vgy|和|k3Vgz|很小，为保证关机后分离有良好的姿态平稳品质，可令k1=k2=k3=0，即为射面内的零射程线导引，由于预关机状态导引段飞行时间较短，各类扰动因素在该段内引起的制导精度散布也较小，因此采用预关机状态导引既能保证制导精度，又能为分离创造良好的姿态平稳条件。

6 仿真

以某两级固体试验火箭二级飞行为例，进行3方面的仿真验证：1)关机点附近导引的平稳性；2)制导精度；3)对干扰的鲁棒性和自适应性。

6.1 仿真条件设置

仿真的发射条件设置如下表1所示，为模拟全射程全方位发射，仿真设置4个射向，每个射向上均设置近、中、远3种射程，同时考虑了姿控系统动态对制导精度的影响，等效姿控系统为典型二阶系统。此外大地模型采用旋转椭球模型(WGS84)。

6.2 仿真结果与分析

基于表1的发射条件设置，对某型固体试验火箭的二级飞行阶段采用本文方法进行仿真验证，其仿真结果如表2所示。仿真中推力、燃速、阻力摄动依据对弹道影响的上下限，按如下组合加入：

表1 发射条件

1) 上偏弹道：推力2%，燃速5%，阻力-20%；

2) 下偏弹道：推力-2%，燃速-5%，阻力20%。

从表2可以看出，通过对各射向下近中远射程的上下限摄动仿真表明，在6.1给出的发射条件设置下，本文算法的再入点最大偏差不超过2.5km，能够满足固体火箭对中制导的精度要求，且对推力摄动、发动机燃速摄动、阻力摄动以及由燃速摄动引起的关机时间摄动(由图5可以看出本文仿真对象的关机时间摄动约为±2.5s)有很好的鲁棒性与自适应。同时，从图5给出的一组指令曲线可以看出，关机点附近的姿态角指令变化平稳，有利于分离稳定。

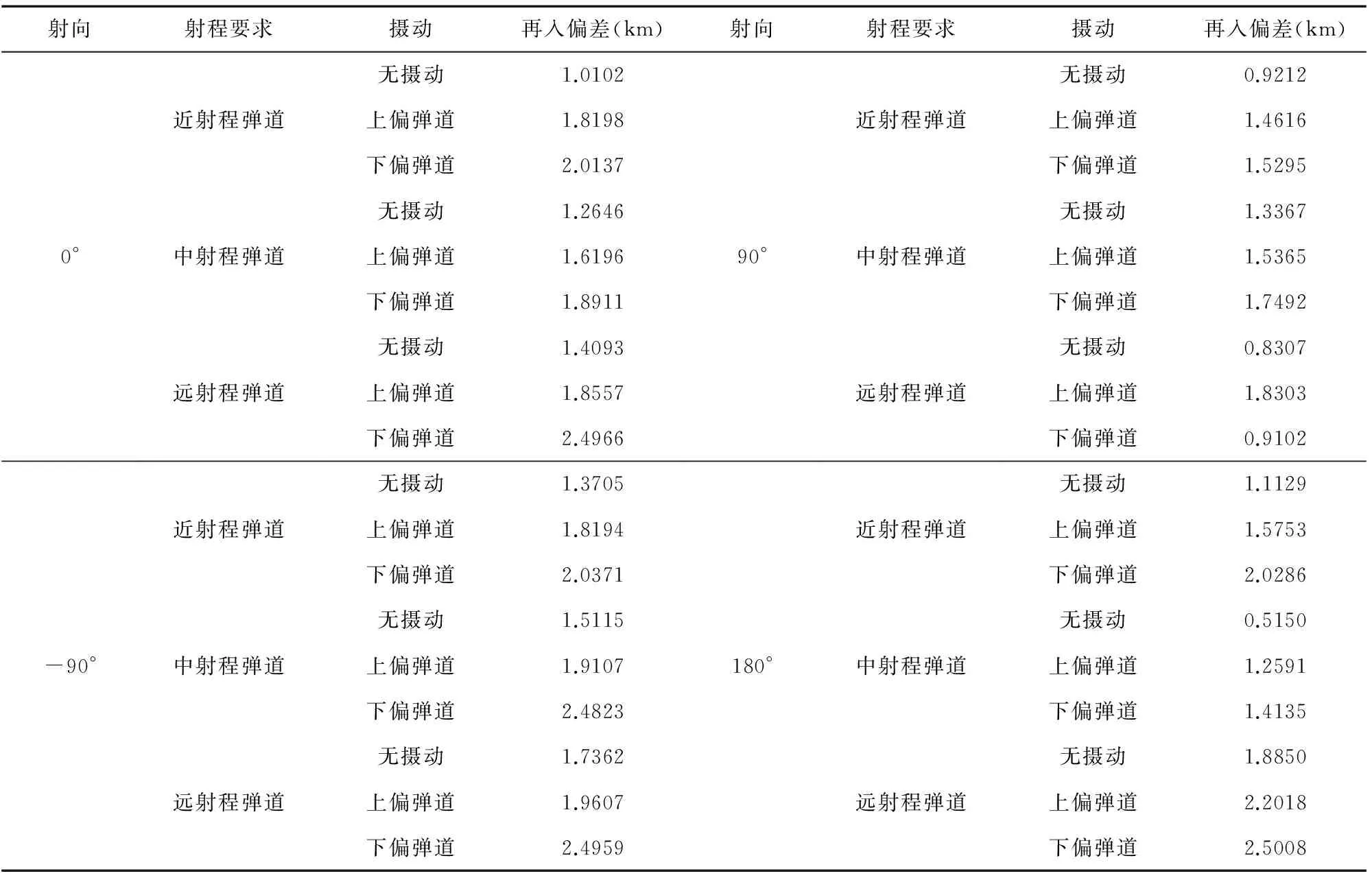
表2 仿真结果

7 结论

针对固体火箭的耗尽关机制导问题，提出了一种基于闭路制导和零射程线相结合的鲁棒自适应耗尽关机制导方法，并进行了仿真验证研究，得到如下几点结论：

1)该方法能够满足中制导的精度要求；

2)该方法对推力、秒耗、关机时间的随机摄动有较强的鲁棒性和自适应性；

3)该方法在关机点附近的指令平稳，利于安全分离。

综上所述，本文方法有效拓展了耗尽关机制导方法的工程化应用。此外需要指出的是，本文方法引入了过渡导引段和末速精确调整导引段，受最大角速率限制，均需要一定的时间，因而能量耗散较大，难以实现最优能量最远射程的导引飞行任务，这是该方法的不足之处。

图5 正东、正西中射程情况下俯仰偏航指令

参 考 文 献

[1] 陈世年.制导系统设计[M].北京:宇航出版社, 1996:216-229.

[2] 王继平,王明海,鲜勇.固体弹道耗尽关机与控制研究[J].弹箭与制导学报,2006, 26(3):64-70.(WANG JiPing, WANG MingHai, XIAN Yong.Research of Depleted Shutdown and Control of Solid Missile[J].Journal of Projectiles Rockets Missiles and Guidance, 2006, 26(3):64-70.)

[3] 廖洪昌,陈奇昌,王明海.耗尽关机闭路制导导引方法研究[J].弹箭与制导学报, 2007, 27(2):35-38.(LIAO Hongchang, CHEN Qichang, WANG Minghai.An Approach to Depleted Shutdown Close-loop Guidance Navigation Method[J].Journal of Projectiles Rockets Missiles and Guidance, 2007, 27(2):35-38.)

[4] 胡正东,郭才发,曹渊,等.轨道轰炸飞行器过渡段轨道设计与制导[J].固体火箭技术, 2009, 32(5):473-477.(HU Zhengdong, GUO Caifa, CAO Yuan, et al.Transition Trajectory Planning and Guidance for Orbital Bombing Vehicle[J].Journal of Solid Rocket Technology, 2009, 32(5):473-477.)

[5] 张毅,杨慧耀,李俊莉.弹道导弹弹道学[M].长沙:国防科技大学出版社, 1999:228-245.