发动机后效段加表数据滤波方法研究

石宝兰 叶振信 杨小龙 付维贤

北京宇航系统工程研究所，北京 100076

固体导弹通常采用耗尽关机方式，当下面级发动机燃烧室压力下降到某一预装订数值时发出上面级发动机点火指令。考虑采用发动机后效段加表测得的视加速度数据作为上面级发动机点火判据，因此作为判据的视加速度数据的准确度将直接影响级间分离发生的时刻，对下面级残余推力、分离的相对速度、上面级起控均会产生较大影响。

导弹飞行过程中，视加速度由惯组中的加表测得。但原始测量数据跳动比较剧烈，直接作为判据使用将带来很大的时间偏差，给级间分离带来不利影响。因此必须对视加速度原始数据进行滤波，以减小数据跳动，提高级间分离时刻的准确性。本文将从滤波平滑度、实时性和计算量3方面对4种滤波方法：动窗平均法、动窗拟合法、频域滤波法及数字滤波法进行对比分析，摸索各自规律，以找到一种适合工程应用的简单有效的滤波方法。

1 问题的描述

某型导弹发动机后效段某秒内视加速度原始数据经归一化处理后如图1所示，图中虚线为所有数据5阶多项式拟合结果。显然视加速度跳动剧烈，跳动幅值最高达0.3m/s2，无法直接作为判据使用，必须滤波。

图1 视加速度原始数据

进行滤波前，先来分析导致视加速度数据跳动的原因，主要有2个：

1)发动机后效段烧蚀不稳定

发动机推力下降段药柱已基本消耗完全，主要烧蚀内壁上的隔热层，其烧蚀过程不稳定，产生的推力本身就是跳动的。易证明推力与视加速度之间存在如下对应关系[1]

2)加表存在测量噪声

导弹飞行过程中存在风干扰、结构干扰等诸多不确定性外部干扰，加表无法辨识这些随机干扰，因而存在系统噪声。同时，加表内部也存在多种电噪声。

2 四种滤波方法

2.1 动窗平均法

动窗平均法是最简单的数据滤波方法。其基本思想是以当前时刻为基准点，往前逐项获取1组历史数据，计算这组数据的代数平均值作为当前时刻的滤波结果。到下一时刻则去掉最早的采样点，补充当前采样点，即数据窗口随时间往后移动，窗口内采样点数量固定不变[2]。

动窗平均法不可避免地会带来时延问题。比如以2N+1个周期为1组数据，其代数平均值应为采样点中间时刻的近似值，以它为当前时刻的滤波结果，必然会带来N个周期的时延。图2展示了窗口周期数为2，10，20时的滤波结果。

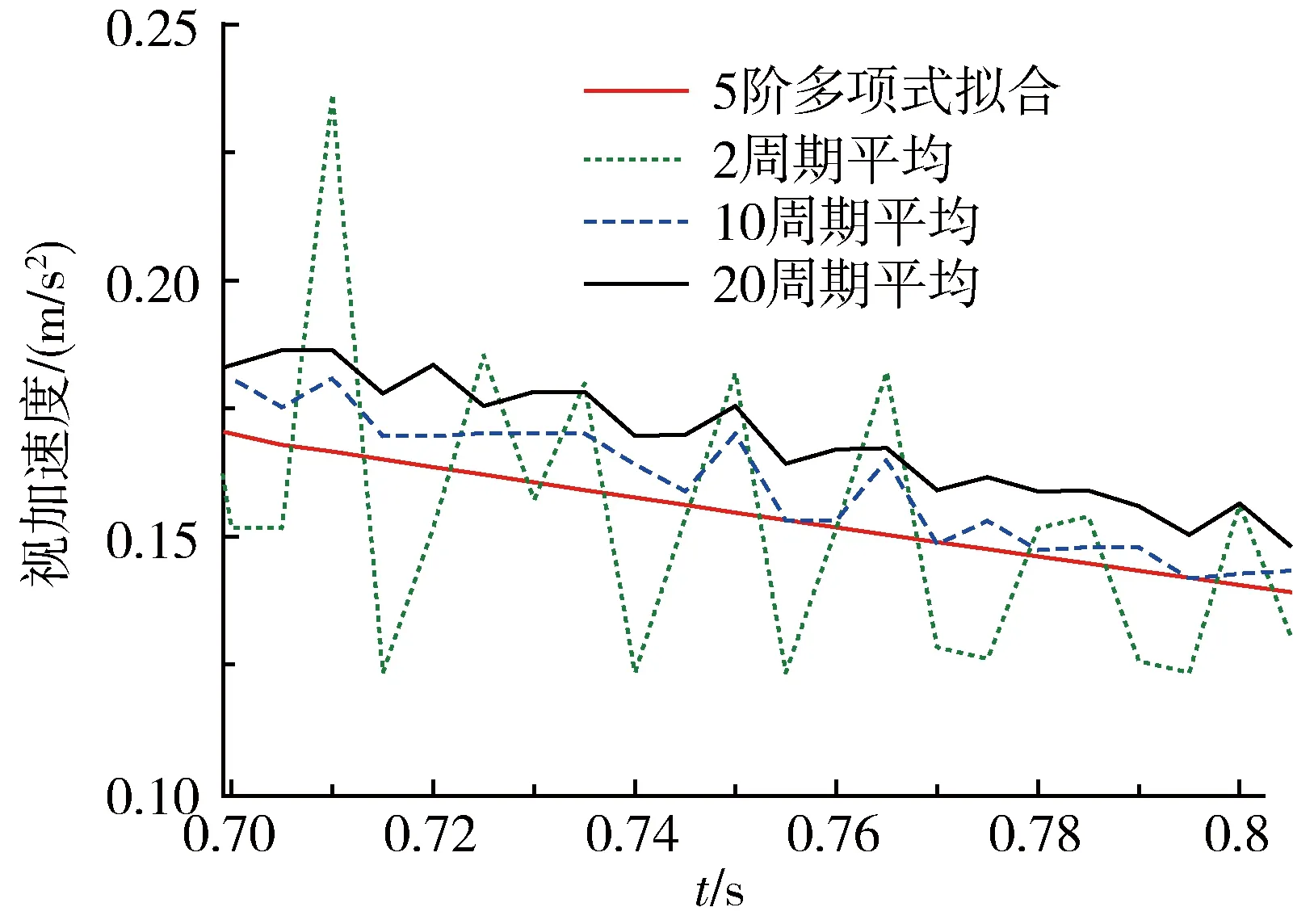
图2 动窗平均法滤波结果局部放大图

从上图容易看出窗口周期数越大，时延越大。此外，还可以看出其滤波平滑度与窗口周期数亦正相关，即窗口周期数越大越能体现平均的滤波效果。工程应用时必需根据具体数据合理选择窗口周期数，周期数太大则时延导致的偏差大，周期数太小则滤波平滑度不好。对于这组数据，仿真结果表明：10周期平均的滤波结果较好，但滤波结果的跳动仍然不够小，存在跳过预装订判据值的风险。

2.2 动窗拟合法

动窗拟合法中的动窗概念与动窗平均法一样，所不同的是对动窗内数据的处理方法为基于最小二乘估计的多项式拟合法。利用Matlab提供的曲线拟合工具箱可以方便地实现多项式拟合，根据拟合多项式计算当前时刻的拟合值作为滤波值。这样的滤波结果是实时的，不存在时延。

2.2.1 设计参数

动窗拟合法的设计参数有2个：拟合阶次与窗口数据量，需要根据原始数据特性仿真确定。

同样其滤波平滑度与窗口数据量有关，而窗口数据量又决定了计算量。图3是拟合阶次固定为3，窗口数据量为40，60，80，100时的滤波结果。

图3 动窗拟合法不同窗口数据量的滤波结果

仿真结果表明在相同的拟合阶次下，窗口数据量低于80时滤波平滑度随数据量增加而提高，高于80时平滑度随数据量增加而提高的程度不甚明显。因此，对于这组数据，窗口数据量选择80比较合理。

现在固定窗口数据量为80，再来分析不同拟合阶次对滤波结果的影响，如图4所示。

如果取所有数据进行一次拟合，显然阶次越高，精度越好。但从滤波结果上来看阶次越高、数据平滑度反而越差。这可能是因为多项式阶次越高对系数的灵敏度越高。不过1阶拟合的滤波结果偏差很大。从原始数据图可以看出，视加速度下降趋势近似于抛物线。因此，对于这组数据，拟合阶次选择2阶比较合理。

2.2.2 预测拟合法

动窗拟合法的滤波结果较好，计算量也可接受，如果能进一步压缩窗口数据量，将更有利于工程应用。为此基于动窗拟合法提出预测拟合法，其基本思想是在动窗拟合法的基础上利用当前时刻的拟合多项式预测下一时刻的数据，当数据更新后，取预测值与测量值的平均值作为当前时刻的数据进行拟合，仍取拟合值为当前时刻的滤波值。预测拟合法比动窗拟合法多了一个预测步，能够利用历史信息部分修正测量值，因此相同窗口数据量和拟合阶次下，其滤波结果要优于动窗拟合法。仿真结果也说明了这一点。

图5 预测拟合法与其它方法滤波结果对比

图5中的第1幅图是拟合阶次均为2阶、窗口数据量均为40的预测拟合法和动窗拟合法的滤波结果对比，可以看出预测拟合法的滤波平滑度更好。第2幅图是2阶、40窗口数据量的预测拟合法和10周期平均法的滤波结果对比，可知当窗口数据量取40时预测拟合法的滤波结果接近于10周期平均法。这说明预测拟合法能够起到压缩窗口数据量的作用。

2.3 频域滤波法

以上滤波方法均为时域方法。加表得到的视加速度数据是时间的显式函数，在时域进行处理是自然的。但是外部干扰与内部噪声也是以时间的显式函数形式叠加在视加速度信号上，要想在时域将它们彻底分开是十分困难的。而在导弹飞行力学环境下，视加速度信号的频谱与干扰信号或噪声的频谱一般是不同的。也就是说，在频域可以实现视加速度信号与干扰信号或噪声的分离，达到滤波目的。这样就产生了频域滤波的思想[3]。作为沟通时域和频域的有效工具，傅立叶变换(FT)和反变换(IFT)使得实现频域滤波的思想成为可能。但是离散傅立叶变换的计算量非常巨大，限制了它的工程应用。在数字信号处理领域中广泛使用的是一种被称为快速傅立叶变换(FFT)的离散傅立叶变换的快速算法，它大大减少了运算量。

频域滤波的基本过程包括3步，如图6所示：

1)利用FFT将被噪声污染的测量信号转换到频域；

2)频谱估计，即：在频域中确定有用信号和各类噪声占据的频段；

3)利用IFFT将有用信号转换回时域。

图6 频域滤波的基本过程

以窗口周期数为5为例，频域滤波结果如图7所示。仿真结果表明，频域滤波结果的平滑度和实时性均非常好。

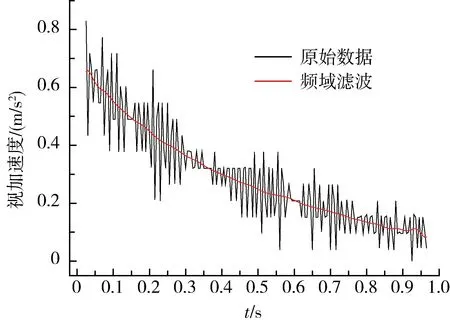
图7 频域滤波结果

2.4 数字滤波法

数字滤波法的核心是数字滤波器的设计。数字滤波器是数字信号处理的一个重要技术分支，其实质是一种用来描述离散系统输入与输出关系差分方程的计算或卷积计算[4]。数字滤波器的设计就是根据要求选择系统h(n)或H(z)，当原始数据通过系统时，对其波形和频谱进行加工，获得人们需要的信号。

按单位冲激响应的样值个数是否有限，数字滤波器可分为有限冲激响应(FIR)和无限冲激响应(IIR)2类；按实现方法和形式不同，数字滤波器可分为递归型、非递归型和快速卷积型3类。本文的目的是寻找一种适合工程应用的滤波方法，所以选择的是FIR数字滤波器，采用非递归法实现，即输出仅与输入有关，与历史输出无关。这样得到的数字滤波器非常简单，计算量小。

利用Matlab提供的滤波器设计箱进行FIR数字滤波器的设计。其系统函数为

即滤波值是当前数据和前N个测量数据的加权平均值，因此也存在时延。容易看出当取h(n)=1/(N+1)时，即退化为动窗平均法。

沿用动窗的思想，本文采用窗函数设计FIR数字滤波器，需要设计的指标有：窗函数类型、滤波器阶数和通带截止频率ωc(Hz)。

与动窗平均法一样，数字滤波器阶数越高，时延越大。另一方面，滤波器阶数太低会影响滤波效果。经多次仿真确定最佳滤波器阶数为10阶。接下来设计ωc。ωc的选择应该保证能够区分视加速度信号和噪声信号，这里有频域滤波的影子。从5阶多项式拟合结果可以看出视加速度信号的趋势项近似为抛物线，频率甚低，而噪声信号频率比较高，两者容易区分。

图8 不同ωc的数字滤波结果

图8展示的是ωc取50，30，10，5和1时的10阶Hamming窗FIR数字滤波器滤波结果。可以看出ωc越小滤波平滑度越好，减小到10以内时，滤波平滑度已经较好，几乎不再提高。因此这里ωc取1。

当采用Hamming窗时，滤波器阶数取10，ωc取1的滤波效果较好。下面再来看不同窗函数类型的滤波结果。除了Hamming窗，常用的窗函数还有2种：Hann窗和Blackman窗。其它设计参数相同的情况下，Hamming窗数字滤波器的滤波效果略好于其余两种，仿真结果的局部放大图(见图9)说明了这一点。

图9 不同窗函数的滤波结果局部放大图

综上所述，最终设计的滤波器为10阶Hamming窗FIR数字滤波器，ωc取1，滤波结果与11周期动窗平均法的结果对比如图10所示。可以看出，在利用同样多历史数据的情况下，数字滤波法的滤波平滑度明显优于动窗平均法。

图10 数字滤波法与动窗平均法的滤波结果对比

3 四种滤波方法的对比

前面通过对每种方法单独分析，确定了各自的最优设计参数。下面对4种方法的滤波结果进行对比并总结各自的特点。11周期动窗平均法、2阶40周期预测拟合法、频域滤波法和10阶Hamming窗数字滤波法的仿真结果如图11所示。

图11 四种方法的滤波结果对比

从图11可以看出：

1)频域滤波结果的平滑度最好，数字滤波次之，动窗平均和预测拟合相对略差；

2)动窗平均法和数字滤波法的滤波结果存在时延，其余方法均为实时滤波；

3)频域滤波结果在某些时段偏离5阶多项式拟合结果较大，且偏差量难以进行补偿。

工程应用时，受弹上计算机运算速度和内存容量限制，滤波方法的计算量不能太大，并且要求实时性好。因此选择滤波方法时要综合考虑在滤波平滑度、实时性和计算量等方面的表现。4种滤波方法的特点总结见表1。

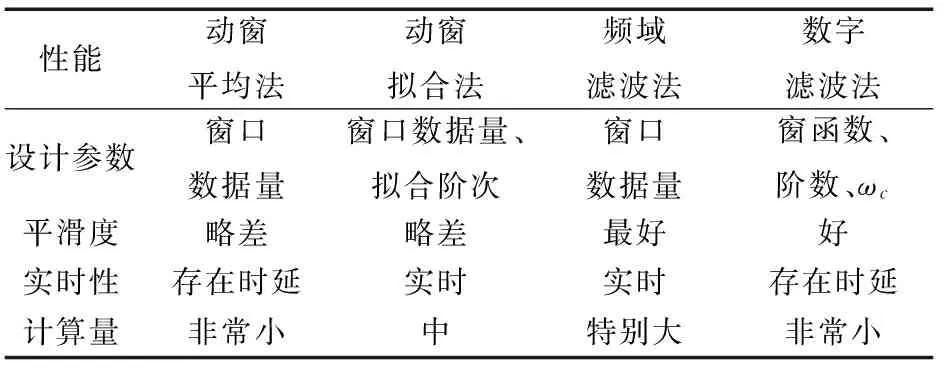
表1 4种滤波方法的特点汇总表

需要特别指出的是，频域滤波的计算量特别巨大，现有弹上计算机的运算速度和内存容量暂时无法满足其要求，在导弹飞行控制中还未见应用实例。从综合表现来看，数字滤波法简单而有效，比动窗平均法更加适合于工程应用。

4 数字滤波法的工程应用

数字滤波法的计算量非常小，滤波平滑度比较

好，能够很好地满足工程应用要求。但也存在不可避免的时延问题，且视加速度数据变化越快，时延造成的数据偏差越大。工程应用时必须对时延造成的数据偏差进行补偿，以提高级间分离时刻的准确性。

级间分离判据诸元必须预先装订好。本质上是以发动机燃烧室压强为判据，根据推力与视加速度之间的关系可以计算出发出点火指令时刻对应的视加速度理论值。考虑滤波方法带来的时延，还要加上数据偏差才能作为视加速度判据诸元的装订值。以10阶Hamming窗数字滤波法为例，其固有的时延为5周期。理论弹道计算可以得到视加速度下降速率，其与时延的乘积作为数据偏差，与视加速度判据理论值相加即可得到视加速度判据诸元装订值。

5 结论

本文从提高级间分离时刻的准确性这一工程背景出发对发动机后效段视加速度数据滤波方法进行了研究，通过对动窗平均法、动窗拟合法、频域滤波法和数字滤波法4种滤波方法的对比分析，得到如下结论：

1)数字滤波法的计算量非常小，滤波平滑度比较好，比动窗平均法更加适合于工程应用；

2)数字滤波法的工程应用必须对时延带来的数据偏差进行补偿，这种补偿体现在视加速度判据诸元装订值上；

3)动窗拟合法滤波效果相对略差，计算量稍大，但实时性好，工程上可以考虑使用；

4)频域滤波法滤波平滑度非常好，但计算量太大，工程上尚难以应用。

[1] 王铮，胡永强．固体火箭发动机[M]．北京：中国宇航出版社，1993．

[2] 邹洪，向大威，景永刚．多普勒计程仪的数据平滑方法[J]．声学技术，2008，27(4)：507-510．(ZOU Hong，XIANG Dawei，JING Yonggang．Data Smoothing Methods for DVL[J]．Technical Acoustics，2008，27(4)：507-510．)

[3] 刘保中．随机噪声的频域滤波方法[J]．战术导弹控制技术，2008(1)：15-17．(LIU Baozhong．Filtering Method Based on Frequency Domain of Random Noise[J]．Control Technology of Tactical Missile，2008(1)：15-17．)

[4] 丛玉良，王宏志．数字信号处理原理及其MATLAB实现[M]．北京：电子工业出版社，2005．