基于改进sPSO算法的测试数据自动生成方法研究
冯 菲,孙玫肖,刘文韬
(中国铁道科学研究院 电子计算技术研究所,北京 100081)
软件测试作为保证软件质量、提高软件可靠性的重要手段,其重要性已经被提升到前所未有的高度。自动化测试能够有效地减轻测试人员的负担并提高测试效率, 因此,对该领域的研究具有重要的理论价值和实际意义。而测试数据自动生成是自动化测试过程中十分重要的环节。
1 测试数据自动生成
测试数据选择作为软件测试中最核心的环节之一,为测试工作指明方向的同时也保障了软件测试结果的有效性。以前生成测试数据最常采用的方法是向前核查和逆向回溯,整个过程由测试人员依据个人经验手工完成,这不仅需要消耗大量的人力和时间,而且具有一定的局限性。为了实现测试数据自动生成,软件测试中的语句覆盖、路径覆盖等问题可以归结为面向路径的测试数据生成问题(以下简称为问题Q)。
问题Q的自动求解为软件测试提供了新的思路,一方面大幅度提高了测试效率,之前需要手工完成的大量重复性劳动被程序的自动执行所替代,另一方面也提高了测试质量,将测试过程中人为造成的错误有效减少,从而保证了测试过程的可靠性。
通过对问题Q的探索和研究,得到了一些具有理论和实际意义的方法,其中基于程序执行的方法是重点,如随机数法、Korel法、迭代松弛法、基于搜索的方法。
基于搜索的方法中以遗传算法为核心算法的测试数据自动生成方法已被广泛研究和改进,目前人们开始研究将其它搜索算法用于测试数据自动生成,以便找到更好的方法生成测试数据,本文以改进后的粒子群算法为核心算法实现测试数据自动生成。
2 粒子群算法及其改进
2.1 粒子群算法
1995年,两位美国学者共同提出了粒子群算法(PSO),他们受早期对鸟类群体行为研究结果的启发,利用生物群体模型,并借用个体学习和文化传递的观念,提出了PSO这一仿生类算法[1]。
基本粒子群算法描述如下:搜索空间维数记作D,粒子个数记作m,粒子i所在位置记作xi=(xi1, xi2,…, xiD),i=1, 2,…, m。将 xi代入适应值函数得到相应的适应值,依据适应值评价xi的好坏。将粒子i的速度记作vi=(vi1, vi2,…, viD)T。记粒子i的个体最优位置为Pi=(Pi1, Pi2,…, PiD)T,全局最优位置为Pg=(Pg1, Pg2,…, PgD)T。每次进行迭代时,根据以下公式更新粒子的速度和位置:

其中,i=1, 2,…, m,d=1, 2,…, D;惯性因子ω≥0;学习因子r1和 r2是两个随机数,介于 [0,1]之间 ;vid∈ [-vmax, vmax],vmax是常数。
2.2 简化粒子群算法
基本粒子群算法中,同时包含了speed和position两个概念,即迭代方程中同时存在vid和xid,在此基础上对粒子群算法进行的改进大都比较复杂,无论是算法本身,算法的实现,还是证明其收敛性。
简化粒子群优化(sPSO)的提出,证明了粒子群的进化过程与粒子速度无关,去掉了粒子速度这一参数,将原来的二阶方程降到了一阶,并证明其收敛性,去掉vid简化后的粒子群方程可表示为:
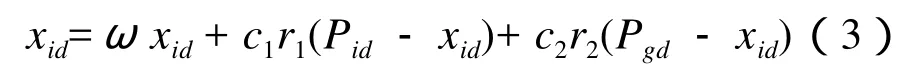
2.3 改进sPSO算法
2.3.1 进一步提高收敛速度
惯性权值作为粒子群算法中的一个重要参数,其主要作用是平衡整个粒子群的全局搜索能力和局部搜索能力,从而显著提高粒子群优化算法的收敛速度。因此,可以从优化惯性权值ω入手,提高粒子群优化算法的收敛速度。
当惯性权值较小时,如果粒子群算法能够找到全局最优解,它所经历的搜索时间很短,即所有的粒子趋向于快速汇聚到一起[2]。当最优解在初始搜索空间内,粒子群算法能够迅速找到全局最优解,否则将永远找不到。当惯性权值较大时,粒子群算法更像全局搜索算法,总是探索新的区域,将需要更多的迭代来达到全局最优,并且更有可能无法找到最优解。
为了平衡整个粒子群的全局搜索能力和局部搜索能力,这里采用不同粒子分别随机在给定范围内对ω进行取值的方法,ω取值范围是[0.6,1.3],这种取值方法平衡了粒子群的全局搜索能力和局部搜索能力,也不会导致算法失效。
另外,学习因子c1和c2分别代表了粒子对自身的学习和粒子群中粒子之间的协作,反映了粒子与群体间其它粒子的信息交流。当c1较大时粒子更倾向于自身经验信息;当c2较大时粒子更倾向于群体经验信息,可能过早的收敛于局部最优值。较理想的情况是,搜索初期,保证粒子的多样性基础上,使算法尽快进入局部搜索,以提高搜索效率;而搜索末期,粒子要保留一定的搜索能力,以摆脱局部极值的干扰。本文利用了线性策略动态调整学习因子,以获得更好的适应值。c1从2.5线性递减至0.5,c2从0.5线性递增至2.5,实现在搜索初期对模型中的“认知部分”进行加强,而搜索后期则加强“社会部分”。
2.3.2 进一步提高收敛精度
sPSO算法一般前期收敛速度可观,后期易陷入局部极值导致收敛速度骤降,影响其收敛精度,这种粒子群算法后期性能下降的状态称为“亚稳定态”。针对亚稳定态问题, 出现了如杂交PSO、变异PSO、模拟退火等添加极值扰动算子的策略,这些方法的共同特点是扰动亚稳定态的粒子,迫使粒子进行下一轮搜索,相比在原地停滞不前更有可能找到全局最优解。这里的触发条件是进化停滞步数t,当t满足需要进行扰动触发条件时同时扰动Pi和 Pg,极值扰动算子为:

其中:ti是个体极值进化停滞步数,tg是全局极值进化停滞步数;Ti是个体极值停滞步数阈值,tg是全局极值停滞步数阈值;r3ti>Ti和r4tg>Tg为两个带条件的均匀随机函数。将上面(4)式和(5)式分别代入公式(3)中,得到:

2.4 基于改进sPSO算法的测试数据自动生成模型
该模型主要包括测试环境构造、改进sPSO算法运行包和测试运行3个部分,各部分之间的关系如图1所示。

图1 基于改进sPSO算法的测试数据自动生成模型
2.4.1 测试环境构造
测试环境构造是整个系统的前提和基础,首先利用程序控制流图进行程序分析,选择需要覆盖的目标路径,选择参数、限定参数取值范围,完成对分支函数以及适应值函数的构造,进行程序插装。
程序插装的前提是要保持被测程序原有的逻辑完整性和正确性,在此基础上在程序中有针对性地插入一些探针,程序的执行过程中通过探针获取一些运行特征数据。通过对这些数据进行分析,从而获得程序的控制流信息和数据流信息,还可以通过进一步分析得到逻辑覆盖等动态信息。适应值函数是粒子群算法与具体应用问题的唯一交互,其构造的好坏直接影响到算法的搜索效率。这里采用“分支函数叠加法”构造测试路径的适应值函数。
2.4.2 改进sPSO算法运行包
改进sPSO算法运行包是系统的中枢,在系统初始阶段提取测试环境构造模块中的参数及其范围,初始化粒子位置,接收测试运行模块的适应值信息,进行判断后应用改进的sPSO算法更新粒子位置,直到找到全局最优解。改进sPSO算法流程描述如下:
Step1:设置算法的相关参数,如粒子数目、粒子维度、搜索范围、迭代次数上限等;
Step2:初始化粒子群,随机生成粒子位置;
Step3:将当前位置写入局部最优集;
Step4:计算每个粒子的适应值;
Step5:找出全局最优值;
Step6:更新全局最优向量;
Step7:更新粒子位置;
Step8:如果未达到结束条件(status=0或达到迭代次数上限),返回Step4;否则输出结果,结束算法。
2.4.3 测试运行
测试运行将系统各个部分连接成为一个整体,完成插装后的被测程序在运行时被调用,将当前参数代入适应值函数,并将得到的适应值发给改进sPSO算法运行包,为算法提供评价个体优劣的依据。
3 实例分析
三角形类别判定程序是在软件测试研究中被广泛应用的一个基准程序,本文利用该程序进行实验仿真,并由C语言实现。分别用sPSO、RIW-sPSO和IMPR-sPSO来生成直角三角形路径的测试数据,并对比这3种算法生成测试数据的运行结果。
当粒子群大小取值固定时(本次实验中取值为100),使用sPSO、RIW-sPSO和IMPR-sPSO这3种算法分别运行20次找到最优解的迭代次数,如图2所示。

图2 实验中找到测试数据的迭代次数统计图
以下是当粒子群大小取值不同时(60递增到160,每次增加20粒子),使用sPSO、RIW-sPSO和IM PR-sPSO这3种算法分别运行20次找到最优解的平均时间,如图3所示。

图3 试验中找到测试数据的时间统计图
图2中黄线明显较蓝线和粉线平稳,没有过大的波动,说明了多次运行时IM PR-sPSO较sPSO和RIW-sPSO找到测试数据的迭代次数相差不大,即算法的稳定性更好;图3中黄线明显较蓝线和粉线位置低,说明了相同粒子数目前提下多次运行时IMPR-sPSO较sPSO和RIW-sPSO找到测试数据的平均时间最短,找到最优解的平均时间最短;综上所述,改进sPSO算法确实在收敛速度和收敛精度两个方面都有提高,从而有效提高了搜索效率。
4 结束语
利用计算机的计算能力自动为目标程序生成高质量的测试数据,已经成为软件测试领域中一个被广泛关注和研究的问题。本文介绍了如何将改进sPSO算法应用于测试数据自动生成的具体实践中。从简单的粒子群算法入手,对其进行简化,并针对其特点和不足从收敛速度和收敛精度两方面入手进行改进,有效地提高了搜索效率。
[1] 严 阳.粒子群算法的改进及其在非线性问题中的应用[D].广东:华南理工大学,2010.
[2] 纪 震,廖慧连,吴青华.粒子群算法及应用[M].北京:科学出版社,2009.
[3] 胡 旺,李志蜀.一种更简化而高效的粒子群优化算法[J].软件学报,2007,18(4):861-868.
[4] 陈琳玲.基于简化粒子群算法的测试数据自动生成方法研究[D].西安:西南大学,2010.
[5] 张艳丽.基于PSO的路径测试数据自动生成方法研究[D].西安:西安科技大学,2008.
[6] Ramamoorthy.C.V. On the automated generation of program test data[J].IEEE Transactions on software Engineering,1976,2(4):215-222.
[7] Kennedy J, Eberhart R. Particle swarm optim ization[C]. IEEE Int Conf on Neural Networks, 1995 .

