多元线性回归理论在数控机床热误差补偿中的应用

田国富，胡 军，郭玉学

（沈阳工业大学 机械学院，辽宁 沈阳 110870）

0 引言

影响机床加工精度的主要原因就是机床各部件的热变形而引起的误差，尤其是在精密加工中，机床热变形所引起的加工误差一般会占到工件加工误差总和的40%～70%［1］，所以对机床热变形误差的预防和补偿就成为提高机床加工精度的重要手段。

机床的热误差补偿就是在机床合适的位置布置适当的温度测量点，从而建立热误差补偿模型；通过建立较好的模型和测量的实时温度值来有效地预测热误差的大小，并将预测值传送到CNC数控系统中，从而实现热误差的实时补偿。在进行热误差补偿的过程中需主要解决两个方面的问题：①温度测点的合理选择；②合适的热误差补偿模型的建立。多元线性回归方法所建立的补偿模型是多个输入、单个输出的数学关系的模型，它不仅能把握住数据群体的主要特征，得到变量间相关关系的数学表达式，利用概率统计知识对此关系进行分析，以判别其有效性，还可以利用关系式，由一个或多个变量值去预测和控制另一个因变量的取值，从而知道这种预测和控制达到的程度，并进行因素分析［2，3］。所以，在研究数控机床热误差建模时运用多元线性回归理论，具备较好的拟合性能、补偿能力和更短的建模时间等优势，另外建模的手段对温度传感器的布置具有更好的鲁棒性［4］。

1 多元线性回归理论模型

1.1 多元线性回归理论的建模方法

利用多元线性回归理论建模，是运用统计方法建立多个输入、单个输出的关系模型，该理论针对加工机床热变形的具体情况，通过实验、计算得到一组表达多个测量点温升输入、单个方向上位移变化输出的线性关系。由于实验时所运用的数控机床的热变形是在X、Y、Z三个不同方向上的，所以必须在每个方向上分别独立地求得一组关系式，最后将各个方向的关系拟合在一起，便可以得到多个输入、多个输出的模型。

假如模型中的因变量y与m 个自变量x1，x2，x3，…，xm存在线性的内在联系，且通过实验得到n组数据：（xt1，xt2，…，xtm；yt），t＝1，2，…，n，那么这批数据有如下结构形式：

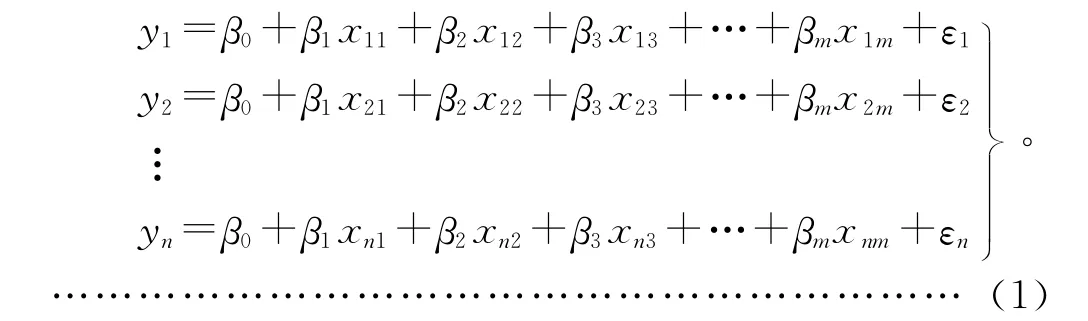
可以得到的多元线性回归模型为：

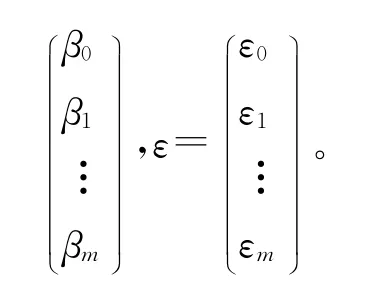
矩阵中的β0，β1，β1…，βm是m＋1个待估计的参数，x1，x2，x3…，xm是m 个可以被测量或者能够被控制的变量，而ε1，ε2…，εn是n个相互独立且服从于同一正态分布N（0，σ）的随机变量，则利用最小二乘法去估计参数β。设b0，b1…，bm分别是参数β0，β1，β2…，βm的最小二乘估计，则回归方程为：

且由参考文献［5，6］可知，可决定系数：

其中：yt＝μ0＋β1xt1＋β2xt2＋ … ＋βmxtm，y＾t＝u0＋

b1x1＋b2x2＋…＋bmxm，μ0、u0均为待定系数。

1.2 建立误差补偿模型

因为数控机床的温度场是连续的，也是随着时间的变化而时刻变化的，所以必须要测量有限个关键点的温度，随后将测得的温度离散化，并利用一定数量的温度传感器测量得到T1，T2，…，Tn。由于数控机床的热变形情况较为复杂，因此利用多元线性回归理论，通过多个关键的温度测点的线性组合来表示热变形与温度之间存在的内在关系：

其中：β0i、βji均为各测温点误差拟合系数；△Ti为各测点的温升；i＝1，2，…，n，为测量点数；j＝1，2，…，k，为测量次数。

2 多元线性回归理论的实例应用

2.1 数控机床热误差分析

本文以数控铣床为例进行研究分析。通过资料和相关的实验得知，数控铣床的热误差主要是由主传动轴的轴向热伸长，主轴在X、Y、Z方向上的热漂移，以及主轴绕X、Y轴的热倾斜而引起的刀具相对于数控机床工作台的移动而产生的。图1为数控铣床的结构筒图。

2.1.1 测温点的选取

要确定温度传感器的个数和测量关键点的位置，主要依据以下三种经验理论：①传感器的个数应大于机床内部热源的个数；②传感器应尽最大可能地靠近热源；③想获得最合适的传感器数量和位置，开始的实验应尽量多设置测温点，以保证重要信息的完整性。根据本课题的需要以及外部条件因素的影响，该研究决定用6个温度传感器（即T1、T2、T3、T4、T5、T6）来进行温度测量。传感器的具体位置和功能如图1所示。

考虑到室温（环境温度）变化对机床热误差建模的影响，令△Ti为各关键测点的温度值与实际室温值T7之间的差。对主轴箱上的6个关键测温点进行模糊聚类分析，再根据各关键测温点的温度变化与机床位移变化的相关系数，从中选出较典型的关键测温点1、2和6，将这3个点进行排列组合，并依据实验所测得的数据，按照公式（4）来计算各个组合的复判定系数R2p，见表1。

图1 数控铣床的结构简图

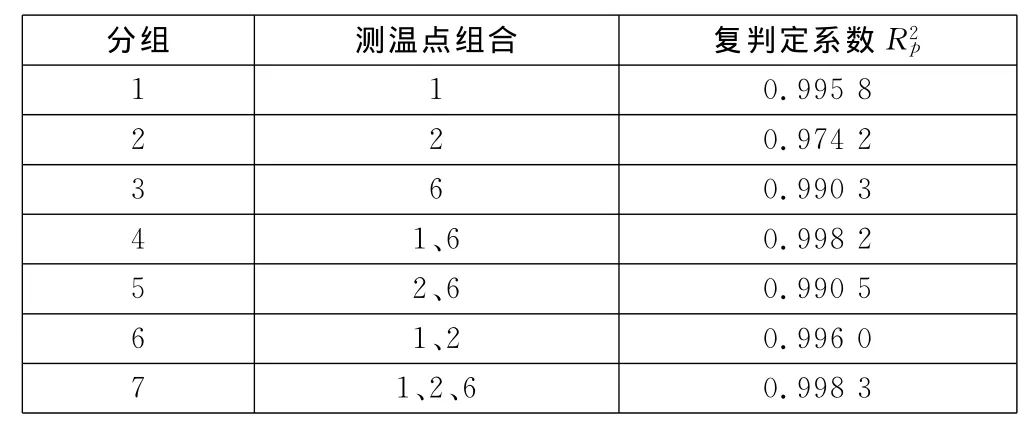
表1 测温点温升和热误差的相关系数

从表1可知，当测点1、6组合时，其复判定系数R2p增大明显；而当1、2及2、6相互两两组合时，它们的复判定系数R2p变化不大；当测点1、2、6组合时，它们的复判定系数R2p与1、6组合时相差无几，可忽略。依据线性回归理论的分析，得出结论：关键测温点2对机床热误差的影响较小，可忽略不计，所以选择机床主轴的前端箱体温度T1和主轴的前端轴套温度T6作为主要测温的关键点。

2.1.2 数控铣床温度值测量与记录

温度值的测量间隔和机床热误差的测量间隔一样，从机床开机开始每5 min记录一次，依据上面测温点的选取方法，本课题总共选定两个主要的温度传感器（T1、T6），每个传感器记录40个温度值，温度传感器T1、T6的温度值记录见表2。表2中，T1为主轴温度，T6为轴套温度。

2.1.3 热误差值的测量

由于机床热变形引起的工件的加工误差，最终体现在刀尖的位移上，该位移误差是随着温度变化的。本实验拟采用激光干涉仪对其加工过程中X、Y、Z三轴的热误差分别进行实时在线测量。

表2 温度传感器测量数据 ℃

由于此数控机床在Z轴方向的进给量不大，而其丝杠的精度相对较高，经过实际的测量后发现在Z轴轴向产生的热误差变化范围很小（－4μm～＋6μm），所以在Z轴方向上产生的热误差值暂且忽略不计。为了完整地表现机床从冷机状态基本达到热平衡状态的情况，选择40组测量数据，测量时间为200 min，测量间隔为5 min。X、Y轴方向的热误差测量值见表3。

表3 X、Y轴向热误差测量值 μm

2.1.4 建立热误差模型

整理实验测得的1、6关键测点温度值以及X、Y方向的热误差，并运用线性回归分析理论即公式（5），可得到以下的补偿公式：

2.2 数控机床热误差补偿

建立的热误差补偿系统结构框图如图2所示。

其具体实施步骤为：①在数控机床上测量1、6关键点的温度数据，计算出数控机床的补偿方程，然后将补偿方程输入到补偿模块中转化为数字信号；②利用系统的补偿模块实时地测量1、6关键点的温度值，并将采集到的数值输入到PLC中，利用其计算功能，将采集的温度值代入到误差补偿方程中去，算出机床所需要实时补偿的X、Y轴方向上的补偿值，最后将计算的实时补偿值传给机床的数控系统进行补偿；③利用机床数控系统本身自带的控制功能，结合可编程控制器计算得出的误差补偿值，来控制数控机床的三轴运动，并改变机床的起始位置，达到实时补偿的目的。本次实验和上次热误差测量时的实验条件完全相同。在数控机床上进行实时补偿后的误差测量结果数据见表4。

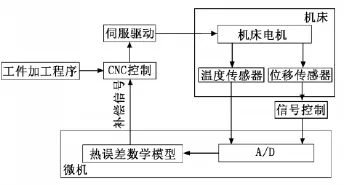
图2 热误差补偿系统结构框图

表4 补偿后X、Y轴向热误差测量值 μm

表4中的数据表明机床进行误差补偿后的精度平均提高了60%左右，说明补偿效果非常好。

3 总结

运用多元线性回归理论建模，不但可以描述数控机床动态的热变形，进行数控机床热误差的模型识别，而且还可以达到非常高的建模精度，可以反映实际运动误差的情况。由于多元线性回归理论包含了更多的数控机床的特征信息，对温度传感器布置的鲁棒性非常好，提高了预测精度。

［1］ 杨建国.数控机床误差综合补偿技术及应用［D］.上海：上海交通大学，1998：2.

［2］ 杜正春，杨建国，关贺，等.制造机床热误差研究现状与思考［J］.制造业自动化，2002，24（10）：1－3，7.

［3］ 倪军.数控机床误差补偿研究的回顾与展望［J］.中国机械工程，1997，8（1）：34－38.

［4］ 方开泰.实用多元统计分析［M］.上海：华东师范大学出版社，1989.

［5］ 费业泰.误差理论与数据处理［M］.北京：机械工业出版社，1981.

［6］ 胡国定，张润楚.多元数据分析方法——纯代数处理［M］.天津：南开大学出版社，1990.