试论序列的拆分与音组含数的排列原则

肖友明

摘要：皮埃尔·布列兹是法国当代著名的作曲家、指挥家，它所创立的音级乘法技术是二十世纪作曲理论的一个代表性体系，这一技术的产生可能与布列兹自幼喜爱数学，并在该领域取得骄人的成绩有关。他通过吸取前人采用简易乘法产生新音高材料经验的基础之上，将其直接或是间接地与数学中的“笛卡尔乘积”理论结合起来，形成其独具特色的技术方法，这一技术是对勋伯格十二音序列技术的发展，可以说它是十二音序列技术的升华。本文就将随着作曲家的思路将音级乘法技术中的序列拆分与音组含数的排列原则进行详尽地分析说明，力求论点明确，论据充分，论证深刻、透彻。

关键词：布列兹 音级乘法 序列拆分 音组含数 排列原则

一、概述

音级乘法技术（Pitch-class Multiplication）是将一个序列原型（prototype sequence）划分成若干个音级组（frequency groups）①，而音级组的产生又是以序列原型中各音级之间的音程级（interval class）为依据，每一个音级组包含若干个音级，其中包含的音级个数称其为音组含数（tone number），再将这些音组含数进行循环排列，产生出多个排列形式，所有的排列形式中的音组两两相乘派生出更为丰富的音高素材的技术方法。

二、十二音序列原型的设计和拆分依据

下面以《无主之槌》这部作品的序列为例进行阐述：

谱例1 《无主之槌》的十二音序列原型（prototype sequence）

序列原型的设计要考虑到音与音之间的音程级（interval class，记为ic）关系，在讨论音程级之前我们要先来看看两种相等原则，其一是八度相等的原则，其二是同音异名相等的原则。在这样两种相等原则的逻辑下，音程级的概念就能明确的进行定义，即是指由两个音之间形成的音级数算数差的绝对值，如上例中按照音级集合原理，假定C音的音级数用数字0来表示（标记为：pn0），那么第一个音就应标记为“pn3”，第二个音应标记“pn5”，这样，第一个音与第二个音的音程级应为∣3-5∣，故其音程级就为“2”。实际上也可以表达为音程中所包半音的个数，但我们发现第三个与第四个音它们所包含的半音数为“11”，像这种半音个数超过“6”的情况，在音级集合原理中我们认为反行关系（mod12）为等值的原则把所有的音程简化为6个音程级，所以像上面提到的这种情况就视为12-11=1，所以它的音程级就等于“1”。由以上这些理论就可以得到如上例中所示的音程级的数字标记。

从以上谱例中可以看出，在这个十二音序列原型中两音之间所包含的音程级有1、2、3、4四种，这就构成了音组拆分的依据，它们一一对应拆分后音组中所包含的音级数量，我们将这种音组中包含的音级数量称为音组含数（tone number），记为（tn）。由此可以得出，如果将上例的十二音序列拆分，所得到的音组含数最少为一个音，最多为四个音，我们将音组中含音级数量最少的音组含数称为最小音组含数，标记为tn（min），并且称含音级数量最多的音组含数为最大音组含数，标记为tn（max）。

由于一个完整的序列原型共包含十二个音，虽然我们将这些音进行了重新拆分组合，但它们的数量相加还是应该等于十二，再有，拆分后的音组含数又是以序列原型中出现的音程级为依据，由此音组的拆分就存在三种情况：第一，由序列原型中出现的音程级的数字相加不足12的情况，称之为不足拆分（insufficient separation），为使其音的总数相加等于12，就将12减去各音程级数字相加后的差数独立成为一个音组。第二，由序列原型中出现的音程级的数字相加刚好12的情况，称之为充足拆分（sufficient separation）。第三，由序列原型中出现的音程级的数字相加超过12的情况，称之为过度拆分（exceeded separation）。

以上三种情况中前两种情况属于准有效拆分（Quasi-valid separation），所谓准有效拆分就说明只满足这种条件是不够的，还得同时满足其它条件才能成立，所需的其它条件将在下文中进行讨论。第三种情况由于音程级数字相加超过了12，由于一个序列原型中音的总数只有12个，所以这种拆分属于无效拆分（Invalid separation），无效拆分就不在我们的讨论之例了。

谱例1中由于音程级数字1+2+3+4=10，故这种情况属于不足拆分，则将剩下的差数分成一组，即是12-10=2。据此，得到序列原型拆分后的音组含数分别为：tn1、tn2、tn3、tn4、tn2。

三、拆分后音组含数的排列原则

经过前面的分析我们知道，谱例1中的音程级数字相加不足12，为不足拆分，它属于准有效拆分，其音组含数分别为：tn1、tn2、tn3、tn4、tn2。那么，要证明该拆分为有效拆分（Valid separation）还必须同时满足第二个条件，那就是音组含数必须要能够按对称原则进行排列，下例就是能够以一个音组含数为对称中心对称的排列。

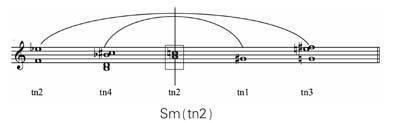
谱例2 以音组含数tn2为对称中心对称的排列

Sm（tn2）

上例是以tn2为对称中心（Symmetry），记为：Sm（tn2），以它为镜面前后音组含数相加的和数分别是4+1=5，2+3=5对称，由此可以得出其对称中心两端的和数是“5”，我们将这种沿对称中心对称的和数称为对称数字（asymmetrical digital），简略记为asd。该排列的对称数字为“5”，记为：asd5。根据上述对称数字的推导方法我们可以得出对称数字的计算公式为：（12-对称中心Sm）÷2。

根据以上的分析，我们可以得出《无主之槌》的序列原型按音程级数字（即音组含数）进行的拆分为有效拆分，这种按照一个对称中心和对称数字为顺序的拆分方式形成的音组含数序列叫做排列（Arrangement），简略记为Ag。那么上面的排列就可以记为：Ag【Sm（tn2），asd5】，读作：对称中心为tn2，对称数字为5的排列。

那么，排列Ag【Sm（tn2），asd5】就只有tn2/tn4/tn2/tn1/tn3这一种情况吗？根据镜面对称原理，显然不只是这一种情况，我们可以得出若干种排列形式。

①tn1、tn2、tn2、tn3、tn4

②tn1、tn3、tn2、tn2、tn4

③tn2、tn1、tn2、tn4、tn3

④tn3、tn1、tn2、tn4、tn2

⑤tn3、tn4、tn2、tn1、tn2

⑥tn4、tn2、tn2、tn3、tn1

⑦tn4、tn3、tn2、tn2、tn1

加上谱例2上的排列形式总共8种，其具体排列方法为：首先取第一个音组含数为tn1，那么第五个音组含数一定为tn4，第二个音组含数就存在两种情况，如果第二个音组含数为tn2，第四个音组含数则为tn3；如果第二个音组含数为tn3的话，那么第四个音组含数则必定为tn2。

图表1 排列Ag【Sm（tn2），asd5】的所有排列形式的可能性

根据上面的推导过程，可以得出上述的排列Ag【Sm（tn2），asd5】总共有八种排列形式，为了使排列表达得更加清楚，下面笔者将对每一种排列形式都进行更为科学地命名。

以tn2为第一个音组含数的排列形式（arrangement form，简略记为af）称为排列形式tn2，标记为af（tn2）。由于每一个音组含数为首的排列都有两种不同的排列形式，如：tn2/tn1/tn2/tn4/tn3；tn2/tn4/tn2/tn1/tn3，我们将第二个音组含数较小的排列下标min，第二个音组含数较大的排列下标max，所以，以tn2为第一个音组含数的排列形式就有两种情况，第一种是排列形式为tn2/tn1/tn2/tn4/tn3，记为Ag【Sm（tn2），asd5】—af（tn2min），第二种是排列形式为tn2/tn4/tn2/tn1/tn3，记为Ag【Sm（tn2），asd5】—af（tn2max），即为谱例1-2-2的排列形式的准确命名。这样一来，每一种排列的各排列形式都有独一无二的名称，也就是说每一个排列的名称都对应着唯一的排列形式。

上面谈到的都是以tn2为对称中心，那么还可不可以以其它音组含数为对称中心呢？根据求得对称数字的公式我们可以得出，如果对称中心为奇数的话求得的对称数字就为小数，而所有的音组含数都是整数，不可能是小数，所以不能以tn1和tn3为对称中心。而以tn4为对称中心则是可行的，如果对称中心为Sm（tn4），那么其对称数字就应为：（12-4）÷2=4，故对称数字为“4”，记为：asd4。接下来我们还需要论证对称中心为tn4，对称数字为asd4的排列在序列原型的音组含数范围内是否成立？我们知道序列原型的音组含数（tn）分别为：tn1、tn2、tn3、tn4、tn2，可以得出除对称中心tn4以外，2+2=4，1+3=4，对称数字asd4是成立的，它们刚好将序列原型中的五个音组含数全部包含在其中了，故对称中心为tn4，对称数字为asd4的排列是成立的，可以将其标记为Ag【Sm（tn4），asd4】。

谱例3 以音组含数tn4为对称中心对称的排列形式Ag【Sm（tn4），asd4】—af（tn1）

Sm（tn4）

上例是排列Ag【Sm（tn4），asd4】的一种排列形式，其它排列形式如下：

①tn2、tn1、tn4、tn3、tn2

②tn2、tn3、tn4、tn1、tn2

③tn3、tn2、tn4、tn2、tn1

加上谱例3上的排列形式总共4种，这里的排列形式为何又只有四种呢？从上面罗列的排列形式不难看出，如果第一个音组含数为tn1，第五个音组含数一定为tn3，那么第二个音组和第四个音组含数就都为tn2，所以这种排列就没有最大排列形式和最小排列形式之分，它可以直接记为Ag【Sm（tn4），asd4】—af（tn1）；如果第一个音组含数为tn2，第五个音组含数一定为tn2，那么第二个音组和第四个音组含数就分别为tn3和tn1，所以这种排列就有最大排列形式和最小排列形式两种，tn2/tn1/tn4/tn3/tn2记为Ag【Sm（tn4），asd4】—af（tn2min），tn2/tn3/tn4/tn1/tn2记为Ag【Sm（tn4），asd4】—af（tn2max）；如果第一个音组含数为tn3，第五个音组含数一定为tn1，那么第二个音组和第四个音组含数就都为tn2，所以，这种排列也没有最大排列形式和最小排列形式之分，可以直接记为Ag【Sm（tn4），asd4】—af（tn3）。

为了更加直观的表述排列Ag【Sm（tn4），asd4】的所有排列形式的可能性，可参看如下图所示的图表。

图表2 排列Ag【Sm（tn4），asd4】的所有排列形式的可能性

以上是序列原型拆分后排列形式的所有可能性，它包括排列Ag【Sm（tn2），asd5】的8种排列形式以及排列Ag【Sm（tn4），asd4】的4种排列形式共12种。每一种排列形式都可以成为音级乘法运算的一个原始素材，可以说它是构成作品音高材料的种子。如何在音级乘法的运算过程中运用这些素材将在接下来的理论中进一步谈到。

四、结语

布列兹是二十世纪整体序列音乐最重要的代表人物之一，他热衷于现代音乐的创作和实验，是当代先锋派作曲家中的佼佼者。其创始的“音级乘法”技术使其音乐大胆而激进，狂热而不失秩序，他将理性思维与音乐表现完美地结合在一起。音级乘法技术开启了音乐创作的一种新的思维模式，为后来的技术理论提供了一些可供借鉴的手段。

参考文献：

[1]齐研.皮埃尔·布列兹的“音级乘法”解读[J]，沈阳音乐学院学报《乐府新声》，2009，（03）.

[2] 黄钟-武汉音乐学院学报[J].1995，（02）.

[3]Pierre Boulez：Boulez on music today，by Faber and Faber London，1971.

[4] Lev Koblyakov：Pierre Boulez A World of Harmony，Harwood Academic Publishers，1990.