让数学教学贴近生活

秦柳银

《数学课程标准》指出：“人人学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展.”在初中阶段，教师要想顺利地完成教学目标，就要努力让学生从“情感”上接近数学；指导学生从“方法”上掌握数学，从“实践”上认知数学.因此，教师要从生活情境入手，引领学生从自己熟悉的生活背景中发现数学，掌握数学和应用数学，体验数学与周围生活的联系，以及数学在社会生活中的作用和意义，逐步领悟学习数学和个人成长之间的关系，感受成功，增进自信.

一、创设生活情境，激发学生的学习兴趣

《数学课程标准》中指出：“教学中不仅要考虑数学的自身的特点，更应遵循学生学习数学的心理规律，强调从学生的生活经验出发，将教学活动置于真实的生活背景之中，为他们提供观察、操作、实践探索的机会……体会到数学就在身边，感受到数学的趣味和作用，体验到数学的魅力.”

初中学生思考问题倾向于依赖直观、具体的东西的支撑.因此，教师在组织教学时，应将学生熟悉的生活情境和感兴趣的事物作为教学活动的切入点，适当地把生活中的图片呈现在课堂之上，有时会达到“一图胜千言”的教学效果.从而激发学生的认知兴趣，让学生不知不觉进入到数学学习中.

例如，在讲解初一年级《图形认识初步》一课时，为了顺利实现帮助学生直观认识立体图形，掌握平面图形的基本知识以及画出简单的三视图及平面展开图，根据三视图画出一些简单的实物图的教学目标.笔者就用PPT向学生呈现了诸多大家比较熟悉的实物图片：足球、纸杯、茶叶罐、魔方和蒙古包等.启发学生从正面、左侧、上侧等不同角度去观察，并试图画出其基本图形.

这样的生活实物图片，不仅拉近了师生之间的情感距离，而且也成为架构起生活与数学知识的桥梁，加之教师的引导，学生会逐渐从生活中去感受数学知识的魅力所在，从而会进一步激发学生学习数学的兴趣.

又如，讲《轴对称图形》这一课，在导入新课时，为了让学生感知数学与生活的关系，笔者创设了常见的生活情境——“蝴蝶飞舞、落下”的课件.在美妙的音乐声中，画面上出现一只色彩绚丽的蝴蝶在花丛中轻歌曼舞，翅膀一张一合地摆动着落在花蕊上，最后将翅膀慢慢地完全收合在一起.在此定格时，笔者提出第一个问题：你从中观察到了什么？为了更突出要观察的问题，笔者又特意将蝴蝶翅膀张合的过程设计为重复演示，接着提出第二个问题：这其中蕴含着什么数学概念？这样找准时机及时引出轴对称图像的概念，由此自然地导入新课的学习.这种运用实例创设学生熟悉的真实情境，学生发现数学就在我们身边，学生在探究活动中感悟了数学，实现了学生以自己的方式自主建构的目的，培养了学生从数学的角度观察生活的意识，提高了学生以生活经验理解数学的能力.

二、探讨生活问题，提高学生的数学应用意识

新课程理念倡导教师引导学生学“有用的数学”，在培养学生数学应用意识和应用能力方面提出了明确要求.数学教育家H·Freudenthal说过，“数学是现实的，学生从现实生活中学习数学，再把所学到的数学应用到现实中去.”众所周知，问题是数学的心脏.生活中我们所遇到的数学问题也比比皆是.如果数学教师能够从中精选一些生活问题在课堂上让学生进行探讨，无疑会提高学生的数学应用意识.

例如，在有关不等式内容的教学中，笔者设计了以下生活中的数学问题，使学生真正感受到了学有所用.

工程类问题：某汽车厂改进生产工艺后，每天生产的汽车比原来每天的产量多6辆，那么15天的产量就超过了原来20天的产量，求原来每天最多能生产多少辆汽车？

销售类问题：某种商品进价为150元，出售时标价为225元，由于销售情况不好，商品准备降价出售，但要保证利润不低于10%，那么商店最多降价多少元出售商品？

记分类问题：某次数学竞赛活动，共有16道选择题，评分办法是：答对一题给6分，答错一题倒扣2分，不答题不得分也不扣分.某同学有一道题未答，那么这个学生至少答对多少题，成绩才能在60分以上？

分房间类问题：若干名学生，若干间宿舍，若每间住4人将有20人无法安排住处；若每间住8人，则有一间宿舍的人不空也不满.问学生有多少人？宿舍有几间？

方案类问题：某公司为了扩大经营，决定购进6台机器用于生产某种活塞.现有甲、乙两种机器供选择，其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算，本次购买机器所耗资金不能超过34万元.

（1）按该公司要求可以有几种购买方案？

（2）若该公司购进的6台机器的日生产能力不能低于380个，那么为了节约资金应选择哪种方案？

在探讨这样的生活问题时，教师要考虑到学生现有的知识水平，要考虑到案例的典型性和功能性，要始终坚持案例为课堂服务的宗旨，调动学生参与课堂教学的热情，并试图用已有数学知识去解决实际问题.这样的设计，不仅贴近学生的生活水平，符合学生的心理需要，而且易于将学习活动介入学生的生命活动、心灵活动，使他们将数学知识和实际生活联系得更紧密.

三、分析生活案例，提升学生的数学迁移能力

《数学课程标准》指出：“数学课程应强调从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步与发展.”

数学在生活中具有广泛的应用空间，教师可以进一步挖掘数学知识在生活中的价值，在课堂上帮助学生分析生活案例，潜移默化的提升学生的数学迁移能力.

例如，在初三总复习“求函数解析式及函数值”有关内容时，笔者注意选取了一些典型的、学生所熟悉的和紧贴时事的现实问题作为例子，以此来激发学生的探究欲望，让学生逐步学会应用有关知识寻求出解决实际问题的方法，提高学生灵活运用数学知识解决实际问题的能力.

【例1】 今年以来，广东大部分地区的电力紧缺，电力公司为鼓励市民节约用电，采取按月用电量分段收费办法.若某户居民每月应交电费y（元）与用电量x（度）的函数图像是一条折线（如图1所示），根据图像解答下列问题：

（1）分别写出0≤x≤100和x≥100时，y与x的函数关系式；

（2）利用函数关系式，说明电力公司采取的收费标准；

（3）若该用户某月用电62度，则应缴费多少元？

（4）若该用户某月缴费105元时，则该用户该月用了多少度电？

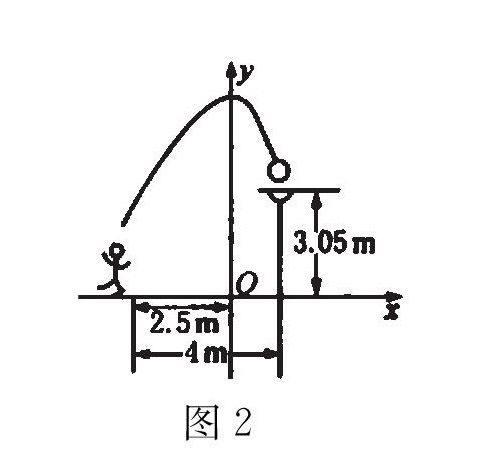
【例2】 如图2所示，一位篮球运动员在离篮框水平距离为4m处跳起投篮，球沿一条抛物线运行，当球运行的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内.已知篮框中心离地面距离为3.05m.

（1）如图2所示的直角坐标系，求抛物线所对应的函数关系式；

（2）若该运动员身高1.8m，这次跳投时，球在他头顶上方0.25m处出手.问：球出手时，他跳离地面多高？

以上两个例题是比较典型的用待定系数法求函数解析式及求函数值的例子，都是以学生熟悉的生活场景为背景，分别勾起学生想到已经学过的一次函数、反比例函数、二次函数的有关知识，此时并要求学生会根据题意和图像特点分析问题，运用待定系数法求函数解析式，从中领悟求三种函数解析式的区别与联系.在复习课中能较好地达到让学生回忆、巩固及应用知识的作用.两道题的最后一小问，让学生更加能感受到函数知识广泛的应用.

四、体验数学活动过程，增强学生的实践技能

著名的教育家陶行知先生指出：“教学是做一件事，不是三件事.我们要在做上教，在做上学……先生拿做来教，乃是真教；学生拿做来学，方是实学.不在做上用功夫，教固不成教，学也不成学.”陶行知老先生的“教学做合一”理论十分重视“做”在教学中的作用.数学来源于现实，也必须扎根于现实，并运用于现实，把数学知识与“做中学”结合起来，既激发了学生的兴趣，又使学生学到了实际知识技能.

如，在学习《图形认识初步》时，可以布置学生课后做设计和制作长方体纸盒的实践活动，让学生更易体会立体图形与平面图形之间的相互转化.

又如，在学习统计的知识时，可以安排学生以小组的形式，通过抽样调查，了解全校各年级学生的视力情况，用统计的方法将调查出的数据进行整理、分析、研究，写出调查报告，从而让学生体会“收集数据——整理数据——分析数据——得出结论”的统计过程.

通过这些实践活动，学生的积极性被充分地调动起来了，积极参与到数学知识的探索和运用中，同时培养了学生的观察、分析和总结的能力，还增强了学生之间的合作和交流能力.

总之，数学来源于生活，生活中处处有数学.在教学过程中，我们要关注学生的生活经验和学习体验，根据实际需要对原材料进行优化组合，灵活处理教材，并选取学生生活中熟悉的人、事、物，采撷生活数学实例，挖掘生活中的数学原型，将抽象的数学概念、定理、公式、法则、规律等化解为一系列学生熟悉的、有趣的、丰富的生活事例，让学生到生活中“找”数学、“想”数学，真切感受“生活中处处有数学”，使学生在生活的舞台上学会运用数学思维去发现问题、分析问题、解决问题，真正引领学生在生活背景下知学、好学、乐学.

（责任编辑 黄桂坚）