书刊拼版：页码中的数学规律

张炼

在工作中，笔者发现胶片上书刊的页码中蕴含着一些有趣的数学规律。了解这些规律，不仅有助于提高工作效率，而且还能让我们感受到工作的乐趣，下面笔者就以16开8页天头规矩的胶订书帖为例（如图1），与大家一起分享页码中的数字奥秘。

加和规律

同一订口相邻两码之和等于本帖次的首末码之和。如图1所示，该书帖首码为1，末码为16，首末码之和为17。第1帖正版中，同一订口相邻两码之和：1+16=4+13=5+12=8+9=17；第1帖反版中，同一订口相邻两码之和：2+15=3+14=6+11=7+10=17。

通过验证，这一规律适用于所有书帖，无论胶订或骑订均可依此类推。不仅如此，骑订的任一帖次的首末码之和恒等，即骑订同一订口相邻两面的页码之和总是等于该书第1帖首末码之和。套帖的每一帖次，其首末码之和的规律同骑订。如书帖中有暗码，可做相应换算。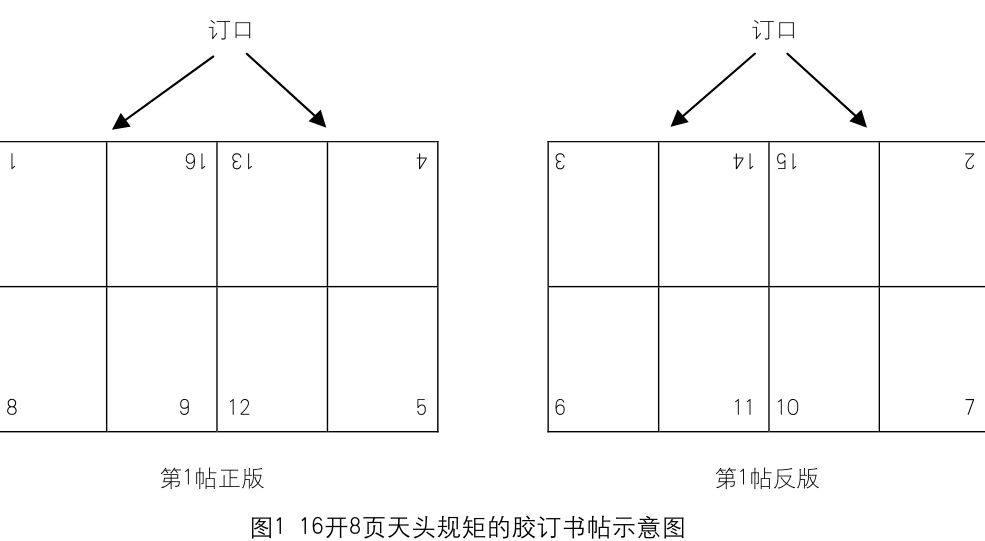

差值规律

每帖正版或反版的页码如按从小到大的顺序排列，则排列后的相邻两码之差均按3、1或1、3规律循环。

如图1所示，第1帖正版页码从小到大的排列为：1→4→5→8→9→12→13→16，每相邻两码之差按3、1规律循环。第1帖反版页码从小到大的排列为：2→3→6→7→10→11→14→15，每相邻两码之差按1、3规律循环。

手工拼版中正版拼版顺序“隔二抽一”就是这一规律的直接运用。所谓“隔二抽一”也就是确定一帖的首末码之后，首先要分出正反版的页码，然后，抽首码 “1”，隔2张胶片，抽“4”码，再抽“5”码，再隔2张胶片，再抽“8”码。依次类推，每帖均是如此分出正反版页码后再拼大版。

积的规律

开本、折页都可以用积的规律来确定。

先看开本的确定。如图1所示，这是一套8页版。如该印刷纸张的幅面为对开，则书刊幅面为16（2×8）开；如该印刷纸张的幅面为3开，则书刊幅面为24（3×8）开；如该印刷纸张的幅面为4开，则书刊幅面为 32（4×8）开。

再看折页的确定。如果是一帖8页折页的版，因2³=8，所以其应为3折页；同理，如果是一帖16页折页的版，因2⁴=16，所以其应为4折页。一般来说，纸张最多4折页，如果一个对开折页的页面上拼有32面，因为2⁵=32，所以其理应为5折页，但为保证折页质量，最好不要这样做，而应将其设计为64开的双联版，或将其设计为对开印刷4开折页的64开单联版。此外，折页方式的确定还要考虑纸张定量及装订方式对折页的不同要求。定量为70g/m²以下的纸张最多为4折页；为了避免折页时出现八字折，80g/m²的纸张在做锁线或骑订时不能采用4折页；如果该书为胶订，则可在折页过程中将书脊、天头等划开排气，这样能有效避免八字折，便可以选择4折页了；157g/m²以上的纸张最多只能进行2折页。