PMSG额定风速以上恒功率多指标非线性控制

赵亚楠，吴昕，梁建华，林春英

(广西大学电气工程学院，广西 南宁 530004)

PMSG额定风速以上恒功率多指标非线性控制

赵亚楠，吴昕，梁建华，林春英

(广西大学电气工程学院，广西 南宁 530004)

讨论了直驱永磁风力发电机组(permanentmagnet wind generatation，PMSG)在额定风速以上时的非线性控制问题。传统的控制方法是采用变桨距风力发电机组或者是调节电磁转矩来达到功率平滑的目的。上述两种控制方法都考虑了风电系统高风速区域时的功率限制策略，但是对系统的转速控制则没有考虑。为了有效减小风电系统高风速区域下的功率和转速波动，在建立风力发电系统非线性数学模型的基础上，利用基于微分几何状态反馈线性化的方法，设计了新的控制策略，即通过同时调节桨距角和电磁转矩来实现风电系统的功率和转速稳定的多目标控制策略，并且仿真验证了该控制策略的正确性和有效性。

直驱永磁风力机;桨距角;电磁转矩;反馈线性化;非线性控制器

广西科学基金资助项目(桂科0728027);

南宁市市校科技合作专项项目(200801029D);

北海市市校科技合作专项项目(北科合200801027)。

1 引言

作为可再生能源发电的一种技术形式，风力发电技术在世界范围内得到了大力的发展。尤其是变速恒频风力发电技术，越来越受到各国的重视。目前，在变速恒频风力发电技术中，应用最广泛的是双馈型风力发电机组，但该机组需要使用齿轮箱将风力机与发电机连接起来，并且随着功率等级的升高，增速齿轮的成本随着单机容量的不断增大而增大，易出现故障，需要经常维护，可靠性差，而且发电效率低。而直驱永磁风力发电机组(PMSG)通过轴系将风力机与永磁风力发电机直接耦合，省去了齿轮箱，既减少噪音又提高了可靠性，因而逐渐受到人们的关注。所以对直驱永磁风电机的研究是很有必要的。

直驱永磁风力发电机的研究主要有最大风能捕获［1，2］和恒功率控制［3］，这两种研究都是以提高风能利用效率为目的的。具体的说就是在风速小于额定风速时采用最大风能捕获的办法，最大限度获取风能;在风速高于额定转速时采用恒功率控制，以较低的风能利用率为代价，实现对电机的保护，以获取合格的电能。

在额定风速以上时，传统的控制方法是采用变桨距风力发电机组或者是调节电磁转矩来达到功率平滑的目的。上述两种控制方法都考虑了风电系统高风速区域时的功率限制策略，但是对系统的转速控制则没有考虑。为了有效减小风电系统高风速区域下的功率和转速波动，本文设计了新的控制策略，即通过桨距角和电磁转矩的同时调节实现风电系统的恒功率和转速稳定的非线性控制。仿真表明，与仅考虑桨距角或电磁转矩调节的恒功率控制策略相比，该控制策略的效果是令人满意的。

2 风力发电机组的建模

2.1 风力机数学模型

风的动能与风速的平方成正比，功率是力和速度的乘积，于是风力机轴上输出的机械功率Pm可用下式表达:

式中:Pm—风轮机捕获的功率，单位MW;

ρ—空气密度，单位kg/m3;

S—风轮扫过的面积，单位m2;

v—实际风速，单位m2/s;

Cp—功率利用系数，是叶尖速比λ和叶片桨距

角β的函数。

式中:ω—风轮转动角速度，单位rad/s;

R—风轮半径，单位m。

如果不算入风力机的刚性系数和阻尼系数齿轮箱惯性，那么风力机的模型可以写为［4］:

式中:J—风力系统的等效转动惯量;

Tm—风力机空气动力转矩，与输出功率Pm的函

数为:

式中:Tem—发电机电磁转矩;

Tβ—桨距角响应的时间常数;

β—桨距角，单位(°)，βr为桨距角的参考值。

2.2 永磁风力电机数学模型

为简化起见，直接给出两相同步旋转坐标系(dq)下永磁电机系统的等效数学模型［4］:

式(4)、(5)中:下标字母表示d，q轴分量。

ud，uq—定子d，q轴电压;

id，iq—定子d，q轴电流;

Ld，Lq—定子d，q轴电感;

rs—定子相电阻;

ωr—转子永磁铁磁场的旋转速度;

ψf—永磁体磁链;

p—微分算子。

结合磁链方程，可得永磁风力发电机的电磁转矩:

式中:pn—永磁机极对数。

根据磁链与电流的关系(4)，式(6)也可写成:

考虑发电机电磁转矩的动态调节，由式(3)、(5)可得整个风力发电系统的动态特性方程:

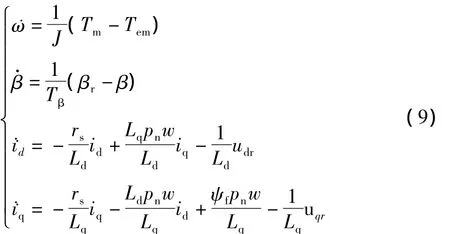
3 控制器设计

3.1 基本控制策略

当风电机组在额定风速以下运行时，浆距角的升高会导致风能利用率的降低，因此只有在额定风速以上时，才考虑浆距角的调节，即风速升高，增大桨距角，风速减小，减小浆距角，通过桨距角的及时调节弥补风速波动带来的风力机输出功率的变动，以便维持风力机输出功率的稳定。当风速超过设计风速或风力机因故障需要退出运行时，将桨距角调整到90度，使风力机的空气动力转矩为最小，以使得风电系统快速退出运行。

在额定风速以上时的恒功率控制主要有以下两种基本控制策略:桨距角控制和发电机电磁转矩控制。

3.1.1 桨距角控制

在这种控制方案中，电磁转矩被设定为一定值，不参与调节;由于桨距角调节速度与风速的变化不同步，所以整个系统的功率会产生波动。

3.1.2 电磁转矩控制

风电系统的输出功率与发电机电磁转矩和风力机的乘积成正比，所以只要保持风力机转速与发电机电磁转矩的乘积恒定不变，就可使得风电系统的输出功率恒定不变。因而可利用电磁转矩的调节实现输出功率恒定的控制，图2给出了利用电磁转矩实现调节实现恒功率控制的控制器结构。

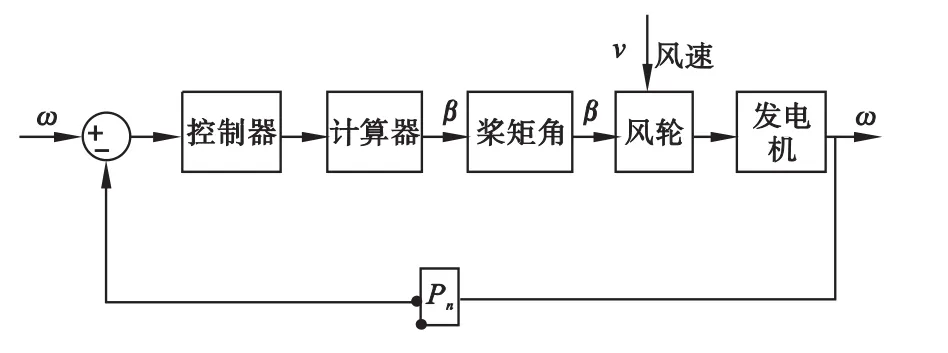
图1 基本桨距角控制器结构图

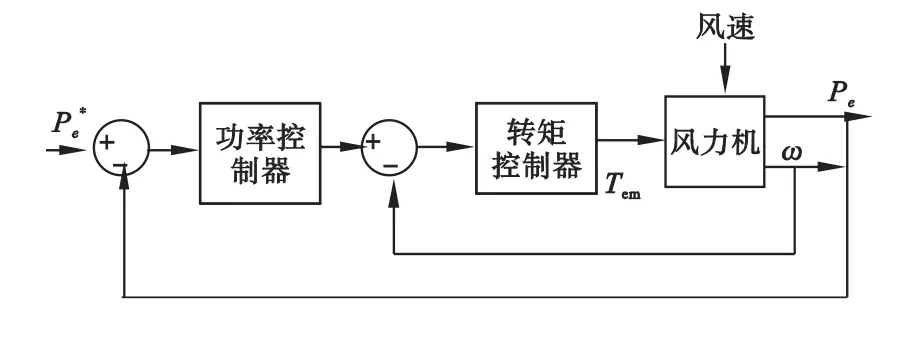
图2 基本转矩控制器结构图

该控制方案能够很好的控制输出功率，但是风电系统的转速发生了非常大的波动［5］。

由上述分析可知:通过单一的调节叶片桨距角或发电机电磁转矩，都难以达到同时减小风电系统的功率和转速波动的目的，因此在本文的设计中，我们考虑了叶片桨距角和电磁转矩的同步控制，以达到减小风电系统的功率和转速波动的双重控制目标。

风力发电系统是一个变量多、耦合性强的非线性系统，基于平衡点线性化模型所设计的控制器很难达到良好地的动、静态性能。基于微分几何的状态反馈精确线性化理论比较成熟的非线性控制理论，它通过选择合适的坐标变换将非线性系统转化为线性系统，对于新生成的线性系统采用线性控制理论进行设计，有效的避免了平衡点线性化存在的问题，且实现起来较为简单。因此，本文采用基于微分几何状态反馈线性化理论来设计控制器。

3.1.3 多指标非线性［6］控制器的设计

由系统(8)可知，系统有3个控制量，，根据基于微分几何状态反馈精确线性化理论，应选择3个输出函数。结合本文的控制目标——同时减小风电系统的功率和转速波动，因此本文选择输出函数如下:*

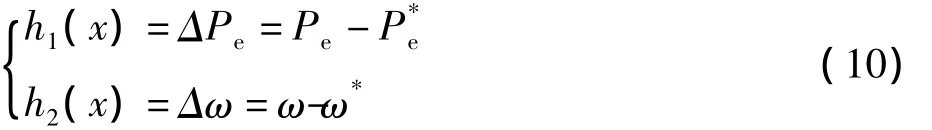
式中:Pe为风电系统电功率，忽略一切损耗的前提下有:Pe=Temω;P*e为发电机额定输出功率;ω*为风力机额定转速。

另外，为了达到完全精确线性化的目的，选择输出函数h3(x)=Δidr－i*dr，i*dr的值可以由负荷的无功功率需求计算得到。

输出函数确定后，根据状态反馈线性化理论可得到系统(8)的闭环控制律为:

为方便叙述，将这一控制策略命名为多指标控制(MC)，控制器结构如图3所示。

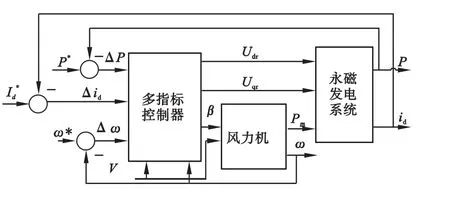
图3 多指标控制系统框图

4 仿真分析

本文研究的重点是在风电系统额定风速以上时，同时减小功率和转速的波动，仿真参数选择如下:P*=2MW，Us=4kV，ω*=2.18rad/s，rs=0.08，Ld=Lq=334mH，J=5000，R=36m，ρ=1.205kg/m3，pn=11，f=50Hz，v=10.8m/s。

功率利用系数Cp与叶尖速比λ和叶片桨距角β的函数为;

上式中;c1，c2，c3为常数。

由于桨叶惯性大，为减少调节器的疲劳和限制桨距角的变化速率。本文中，参考桨距角在(0°～90°)的区域内变化，桨距角变化率设定在(－5°/s～+5°/s)范围内。

图4为仿真所采用的风速波形，图5～7显示了在给定风速下，仅考虑桨距角控制(BC)、仅考虑电磁转矩控制(TC)和本文所设计的多指标控制策略(MC)实现恒功率控制时的风力机转速和输出功率的仿真结果。

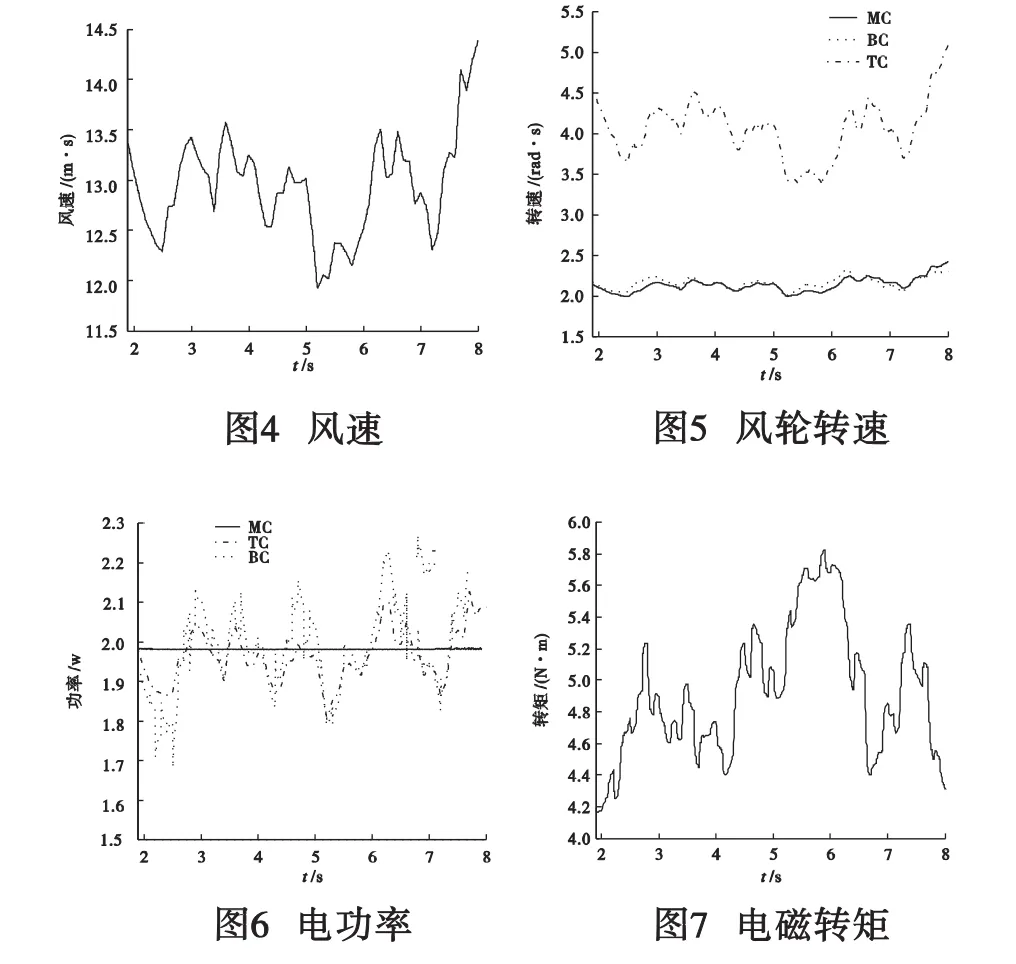
图5～7中的BC控制为仅仅考虑了桨距角时的恒功率控制策略，TC控制为仅仅考虑了电磁转矩时的恒功率控制策略，图7为仅考虑电磁转矩控制时的输出电磁转矩。

(1)由图5可知，仅考虑电磁转矩控制时，系统转速波动较大。这是因为系统输入的机械能增加(或减少)，而系统的输出功率维持不变，多余的能量必然会去增加(或减少)转速，从而导致转速的大幅度变动。

(2)由图6可知，仅考虑桨距角控制时系统的功率波动较大。其主要原因在于:电磁转矩被设定为额定值不变，风速变化所引起的系统输入机械能的变化需要由桨距角的调节来维持稳定，而桨距角的响应速度较慢，因此在桨距角的响应过程中不可避免地出现功率波动。

(3)对比图7和图5中TC控制下的转速变化趋势可知，电磁转矩的变化与转速变化的趋势是相反的。这是因为风速变化将引起系统转速的变化，而为了维持输出功率不变，电磁转矩必然与转速成反方向变化，这也从另一个角度解释了仅靠调节电磁转矩不能够维持转速稳定的原因。

(4)对比图5和图6可知，与仅考虑桨距角和仅考虑电磁转矩调节的恒功率控制策略相比，本文所提出的多目标控制策略不仅能够很好地维持系统输出功率的恒定，而且还能够有效减少系统的转速波动。其原因在于:电磁转矩的迅速调节可以有效减少风速变化所引起的功率变化，而桨距角的调节又可以调节输入系统的机械功率，从而使得系统的转速波动减小。

5 结论

本文分析了传统的控制策略—电磁转矩控制和桨矩角控制的优缺点。上述两种控制方法都考虑了风电系统高风速区域时的功率限制策略，但是忽略了对系统转速的控制。为了达到同时减小风电系统高风速区域下的功率和转速波动的目的，本文设计了新的控制策略，即通过同时调节桨距角和电磁转矩来实现风电系统恒功率和转速稳定的多指标控制。Matlab/simulink仿真证明了该控制策略的有效性和正确性。

［1］ 田友飞，李啸骢，徐俊华，等．变速恒频双馈风电机组最大风能捕获非线性控制策略［J］．电力系统自动化，2011，35(11)．

［2］ 薛娟妮，直驱风电系统最大功率捕获技术的仿真研究［D］．广西大学，2008 －11．Xue Juan-ni．Direct-drive wind power system simula．

［3］ 姚红菊，赵斌．变速恒频风电机组额定风速以上恒功率控制［J］．能源与环境，2004，5(3):12 －13．

［4］ 王彦国．直驱式风力发电系统及其控制策略［D］．华北电力大学(北京)2009－08．

［5］ Chinchilla M，Arnaltes S，Burgos JC．“Control of permanent-magnet generators applied to variable-speed wind-energy systems connected to the grid，”Energy Conversion，IEEE Transactions on，vol．21，no．1，pp．130 －135，March 2006．

［6］ 李啸骢，程时杰，韦化，等．输出函数在多输入多输出非线性控制系统设计中的重要作用［J］．中国电机工程学报，2006，26(9):87－93

［7］ 卢强，梅生伟，孙元章．电力系统非线性控制［M］．2版．北京:清华大学出版社，2008，10．

［8］ 廖勇，何金波，姚骏，等．基于变桨距和转矩动态控制的直驱永磁同步风力发电功率平滑控制［J］，中国电机工程学报，2008(18)．

［9］ 陈思哲，吴捷，姚国兴，等．基于微分几何的风力发电机组恒功率控制［J］．控制理论与应用，2008，25(2):336 －340．

［10］ 张博．风力发电及风力机模拟系统的研究［D］．华北电力大学，2010．

［11］ 胡雪松，孙才新，廖勇，等．直驱永磁同步风力发电机转矩动态滑模控制策略研究［J］．重庆大学学报(自然科学版)．

［12］ 尹明，李庚银，张建成，等．直驱式永磁同步风力发电机组建模及其控制策略电网技术［J］，2007(15)．

［13］ Mansour M，MansouriM N，MimouniM F．“Study of performance of a variable-speed wind turbine with pitch control based on a Permanent Magnet Synchronous Generator，”Systems，Signals and Devices(SSD)，2011 8th International Multi-Conference on，vol．，no．，pp．1 －6，22 －25 March 2011．

Multi-index Nonlinear Control of Constant Power Output for the Permanent M agnet W ind Turbine Generation

ZHAO Ya-nan，WU Xin，LIANG Jian-hua，LIN Chun-ying
(College of Electrical Engineering，Guangxi University，Nanning 530004，China)

This paper discusses direct drive permanentmagnetwind generatation(PMSG)'S nonlinear control problem above the rated wind．The traditional controlmethod is using variable pitch wind turbines or regulating the electromagnetic torque to smooth power．Both of the two controlmethods considered the problem of power limitation，but the speed control is ignored．In order to effectively reduce the fluctuation of power and speed during the high wind speed region，this paper based on the established nonlinearmathematicalmodel for the wind system，takes advantage of the differential geometry state feedback linearization，designes a new control strategy，that is，through adjust pitch Angle and electromagnetic torque at the same time to realize power and speed's stability which is the heart of themulti-objective control strategy，Simulation results show that this control strategy is correct and effective．

PSMG;pitch angle;electromagnetic torque;feedback linearization;nonlinear controller

TM57

B

1004－289X(2013)03－0020－05基金项目:国家自然科学基金资助项目(51267001);

2013－03－29

赵亚楠(1987－)，女，新疆人，工学硕士研究生，2010年就读于广西大学电力系统及其自动化专业，攻读硕士学位，研究方向为电力系统分析与控制;

吴昕(1983－)，男，湖南益阳人，硕士研究生，研究方向:电力系统智能测量与智能控制、无线传感器技术。