基于ANSYS有限元法的接触系统电动力分析
黄蔚偈,兰太寿,刘向军
(福州大学电气工程与自动化学院,福建 福州 350108)
上的磁感应强度相关,而作用在触头上的磁感应强度主要由触头的收缩
基于ANSYS有限元法的接触系统电动力分析
黄蔚偈,兰太寿,刘向军
(福州大学电气工程与自动化学院,福建 福州 350108)
继电器接触系统电动力主要由触头的HOLM力和导体的洛伦兹力组成。在冲击电流试验中,触头是否因电动力作用而斥开是考核电能表用磁保持继电器安全性和稳定性的重要标准。首先通过有限元法结构分析,计算动静触头的接触半径,再通过耦合场分析计算接触系统各部件的电流密度分布和磁场分布,进而求解出电动力。对不同触头压力和不同短路电流下的电动斥力进行了计算与分析,并研究了接触系统各部件对电动力的影响,为接触系统的改进提供基础。
磁保持继电器;电动力;接触半径;有限元分析
1 引言
当电流流过电器触头时,由于触头实际接触面积很小,在接触区域附近会发生电流线收缩,产生电动斥力,即Holm力。而通有电流的导电臂在周围空间磁场的作用下,也会产生洛伦兹力,这两种力的合力构成了接触系统的电动斥力。在额定电流作用下该电动斥力比较小,对电器稳定性影响不大。但当触头系统承受冲击电流时,导电臂和接触表面的电流线密度急剧增加,空间磁场也成倍增长,此时感应出的电动力有可能使闭合的接触系统斥开,产生严重的后果。标准要求电能表用磁保持继电器的抗冲击电流能力为额定电流的30倍,比一般磁保持继电器的5~10倍要高得多。当进行冲击电流试验时,触头可能发生斥开现象,因此,电动斥力的研究对电能表用磁保持继电器的安全性和稳定性有重要的意义。
电动斥力与接触系统可动部件的电流密度和磁感应强度有关,因此,求解出各部分的电流密度和由电流产生的磁感应强度是准确求解电动力的关键。不同的电器接触系统型式多样且复杂,电流密度和磁感应强度用解析法较难求出,因此用传统的电动力计算公式有一定的误差,不能准确考虑到接触系统电流密度的分布对电动力的影响。
随着有限元计算软件的发展,通过电流传导分析和耦合场分析可以精确计算出接触系统的电流密度分布和相应磁感应强度的分布,通过一定的后处理,便可方便计算出电动斥力 。本文基于有限元软件ANSYS,先通过结构分析计算出不同触头压力下的接触面积,以此为基础分析不同触头压力和不同短路电流对电动斥力的影响。
2 接触系统结构分析
动静触头的实际接触面积很小,且离散分布,一般取一等效的中心圆形导电斑点来计算。实际的接触面积与触头压力、触头的几何形状和材料有关,运用传统计算接触半径的公式估算弹塑性变形的量,存在着误差。而在运用有限元进行结构分析时,由于可以根据触头的实际结构建立模型,材料属性包含了应力应变曲线,而且根据要求可以施加不同的载荷,因此可以较好地分析触头的实际弹塑性变形,能较为准确地求出接触半径[5],结构分析的流程如图1所示。图2为动静触头结构分析的有限元模型,由于要对接触体进行分析,所以在可能的接触区域建立接触对。触头具有轴对称性,因此只需建立1/2的二维模型。
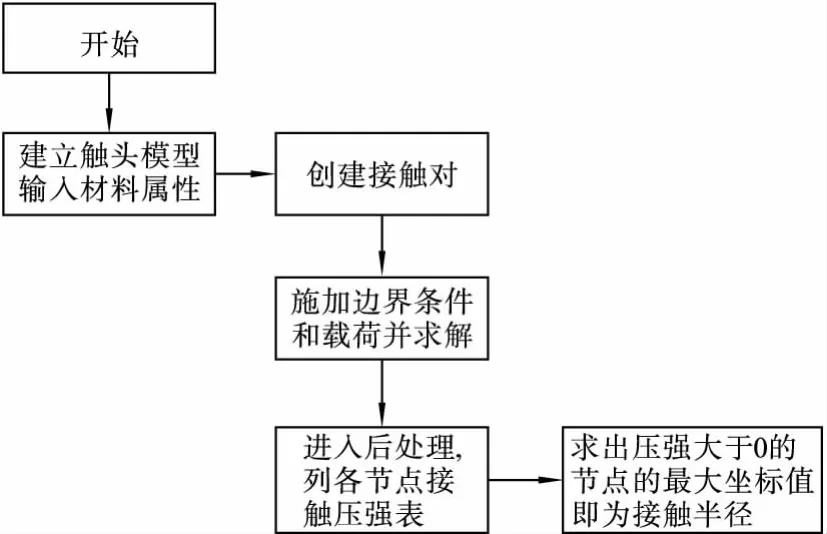
图1 求解接触半径的ANSYS结构分析流程图
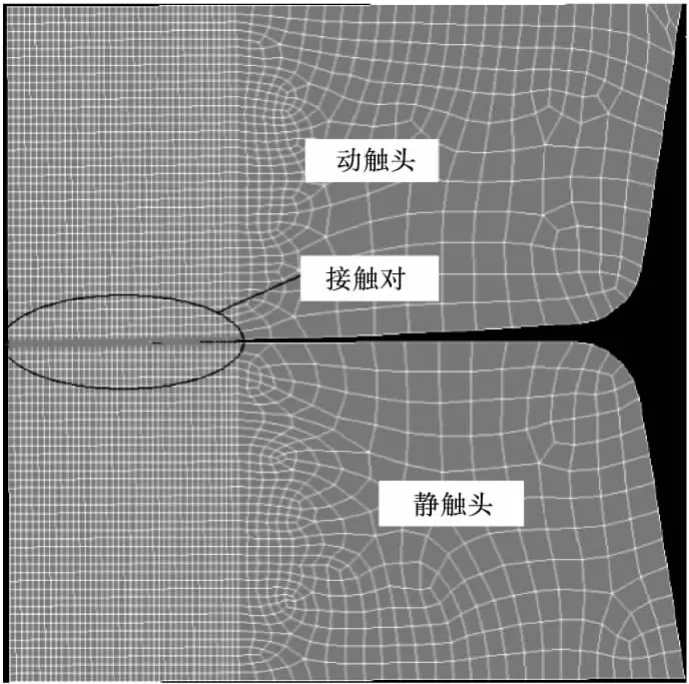
图2 触头结构分析的有限元模型
由有限元结构仿真分析和公式法计算得到的接触力与接触半径关系如表1所示。公式法计算采用工程上常用的计算公式:

其中是引入的参数,用来衡量触头表面光滑度和变形程度,其值介于0.3与1之间,接触表面越光滑,变形越塑性,ξ越接近于1,反之则越接近于0.3。

表1 有限元法与公式法计算得到的接触半径的比较
利用三维制图软件建立接触系统模型如图3所示。将该模型导入ANSYS中并建立包含接触系统的外围空气体模型。本文所研究继电器动触头为球面,静触头为圆柱面,建模时使球面与圆柱面相切,以切点为圆心建一圆周并向球面拉伸成圆柱型导电桥以模拟接触面[2,6],圆柱的半径据上表得出,此模型可以模拟在实际接触区域的电流线收缩效应。

图3 接触系统的三维模型
3 电磁耦合场分析及电动力计算原理
本文利用ANSYS的电流传导—静磁耦合分析进行电动力的计算。首先对接触系统进行电流传导分析。计算出导电体各个部分的电流密度,再将计算结果载入静磁分析中作为载荷。图4为电流传导分析得到的接触系统电流密度分布矢量图,从图中可以看到在接触区域有强烈的电流收缩效应。通过静磁分析可以计算出每个单元的电动力矢量。所分析的接触系统可动部件主要为动触头和与之相联的簧片,只有作用在这两部件上的力才能导致触头斥开。由于Holm力本身也是洛伦兹力,因此电动斥力均可按照洛伦兹力公式FL=∫∫∫J×BdV进行计算。如图4所示坐标系,电动斥力只有X轴分量才能使触头斥开,并且由于簧片一端固定,因此以力矩的形式来计算,将积分化为单元求和,即:M=∑v1FLx·LY+∑v2FLX·LY,其中v1,v2分别表示簧片和动触头,LLX表示网格单元的洛伦兹力的X轴分量,FY表示网格单元质心到簧片固定端的距离的Y轴分量。由于网格单元划分足够细,两者乘积即近似网格单元的斥力力矩。对两部分所有网格单元进行求和可分别得到两部分的总斥力矩。
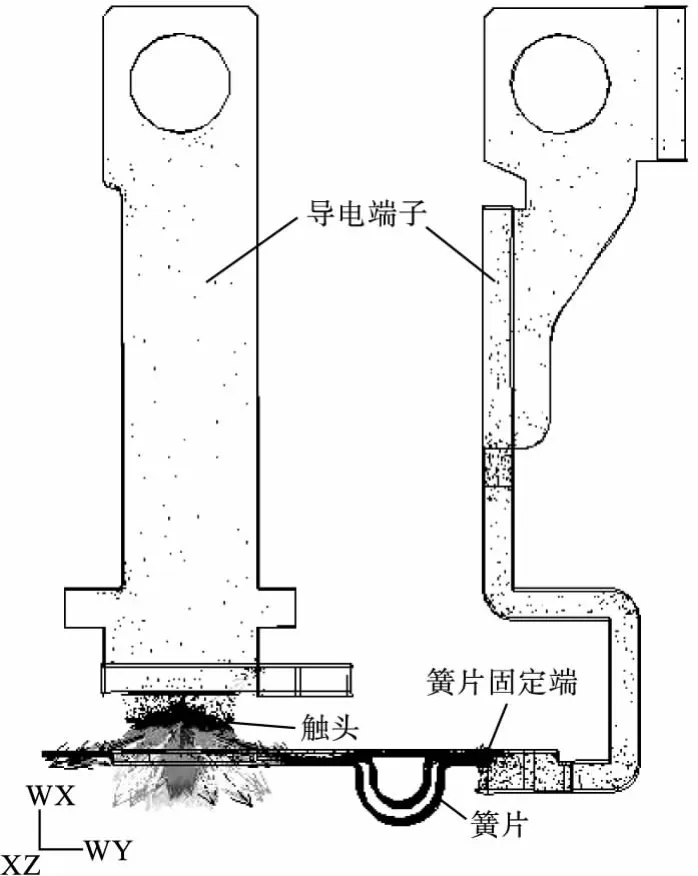
图4 电流密度分布矢量图
4 电动力计算及结果分析
4.1 电动力的计算
本文将对不同电流和不同触头压力对电动斥力的影响进行分析,分别用有限元法和公式法对电动斥力进行计算,其中公式法采用以下公式[6,7]:

式中,B为接触导体截面半径,单位为mm,由公式(1)得到;F为触头压力,单位为N;H为材料布氏硬度,单位为N/mm2。
设置的分析实验如下:①根据上述有限元法结构分析计算2.5N触头压力下得到的结果建立电动力分析模型,输入不同的电流值进行电动力计算和分析。②以继电器的30倍额定电流即2400A作为有限元模型的输入载荷,改变接触半径进行计算和分析。由于接触系统为拍合式,两种情况的计算结果转化成对簧片固定端的力矩进行比较。
图5是接触半径不变,改变输入电流所得的仿真和计算结果,图中的标幺值是以1000A时的有限元仿真结果作为基值进行归算。
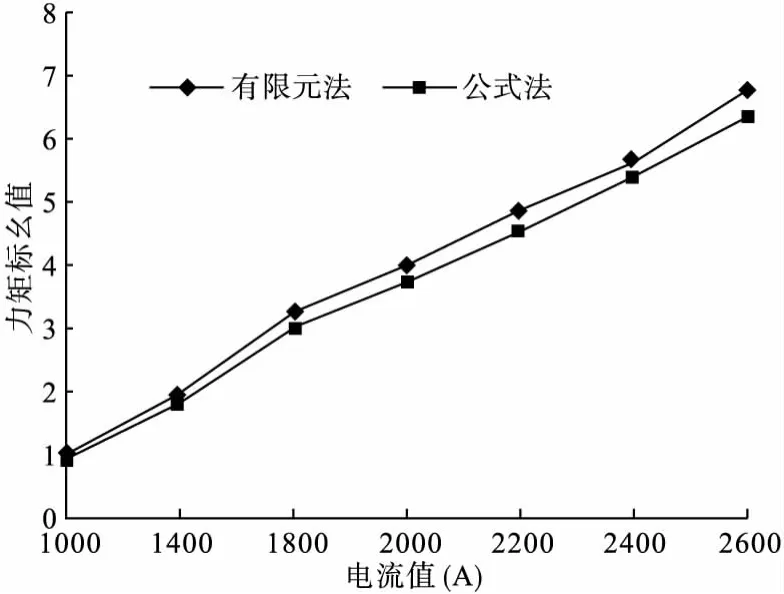
图5 2.5N触头压力下不同电流的电动力计算结果
图6是输入电流不变,改变接触斑点半径所得的仿真和计算结果,图中的标幺值是以接触半径为0.102mm时的有限元仿真的结果作为基值进行归算。
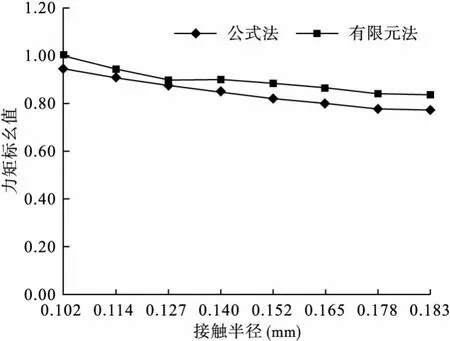
图6 2400A电流下不同接触半径的电动力计算结果
从图5和图6可以看出有限元法与公式法的结果比较吻合。
4.2 接触各部件对电动斥力的影响分析
由于电动斥力来源于簧片的洛伦兹力和触头上的Holm力,为研究两者在总的电动斥力中所占的比重,以2400A作为输入载荷对不同的接触半径下的电动力进行仿真分析,结果如图7所示。由图中可以看出触头部分的斥力是产生电动斥力的主要原因,随着触头压力的增大,接触半径增加,电流收缩效应对电动力的影响呈减少趋势。而簧片上电流密度分布与接触半径关系不大,在图中近似水平直线。
根据洛伦兹力公式FL=∫∫∫J×BdV可知,触头上的电动力的产生不仅与电流线收缩有关,还与触头
上的磁感应强度相关,而作用在触头上的磁感应强度主要由触头的收缩
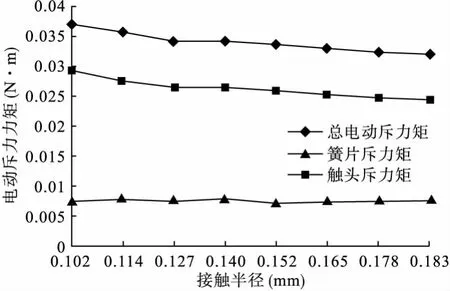
图7 簧片洛伦兹力、触头Holm力和总电动斥力比较
电流和触头簧片、导电端子的电流感应而来。为研究触头簧片和导电端子对触头电动斥力的影响,设计如下仿真分析,即对不同的接触半径进行电流传导仿真,并将结果分两种情况分别导入到静磁场分析中:①将接触系统所有部件的电流仿真结果作为载荷导入到磁场分析中;②只将动静触头的电流仿真结果作为载荷导入。由于电流传导分析是对整个接触系统进行,因此能反映真实的电流分布情况。在分别导入静磁场分析时,两种情况下动静触头的电流分布是一致的,唯一的区别是其他导电部件上是否加载有电流。这样就可以较好地分析触头簧片和导电端子的影响。结果如表2所示。
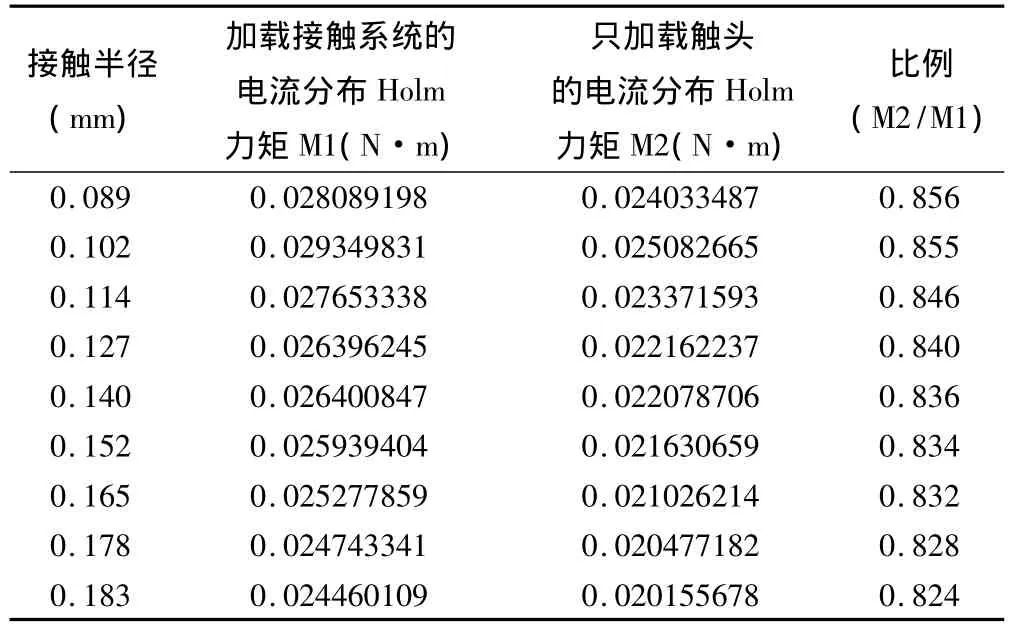
表2 加载接触系统的电流分布和只加载触头的电流分布的Holm力矩仿真结果对比
如表2所示,加载整个接触系统电流分布所产生的Holm力大于只加载触头电流分布两者所产生的Holm力,表明产生触头电动斥力的磁感应强度虽主要来源于触头本身的电流线收缩,但周围导体(如触头簧片和导电端子等)的电流在触头感生的磁场也不能忽略。如表2中的比例所示,收缩电流与其自身感应的磁场相作用产生的斥力占触头电动斥力的百分之八十几,其余为周围导体产生的磁场对电动斥力的影响,而且随着接触半径的增加,周围导体对斥力的影响增大。因此在设计时须考虑导电回路对触头可能造成的影响并尽量减少。
4.3 触头压力对电动斥力的影响分析
触头上的电动斥力的大小与接触斑点的面积有关,在材料相同时,接触斑点的面积取决于触头压力,因此触头压力减少将导致触头上的电动斥力增大,当电动斥力大于触头压力时将导致触头斥开。为考察触头压力与电动斥力的关系,分别从2N到5N进行触头的结构力学分析,求出不同触头压力下的接触半径,并以2400A为电流载荷,导入电流传导—静磁耦合场进行电动斥力分析计算,结果如图8所示。
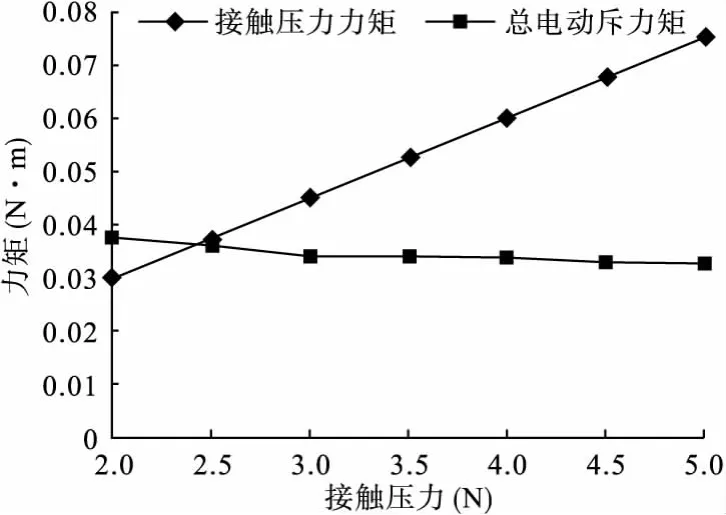
图8 接触压力力矩与电动斥力力矩的关系
从图中可以看出,当短路电流为2400A,触头压力在2.5N时其力矩与电动斥力力矩已相当接近,此时有可能发生触头斥开现象。因此,设计的继电器时应使触头在闭合时有大于2.5N的触头压力,并留有一定的裕值。
5 结论
本文利用ANSYS软件作为有限元计算工具,对磁保持继电器的接触系统进行电动力的仿真计算与影响因素分析,并与传统工程上运用的公式法进行比较。
通过结果分析与比较可得,不论是结构分析抑或耦合场分析,有限元法与公式法计算结果相近,但有限元法在结构分析中能直接反映触头结构和弹塑性变形对接触半径的影响,在耦合场分析中能准确计算复杂结构的电流密度和磁感应强度的分布,这都有利于电动力的准确求解和分析。通过对电动力中触头Holm力和导体洛伦兹力的分析可知,Holm力是电动斥力的主要成份,但导体的洛伦兹力也不可忽略,而且导体中电流感生的磁场对触头Holm力也有一定的影响。
[1] Monnier,B.Froidurot,C.Jarrige,R.Meyer and P.Testé.A mechanical,electrical,thermal coupled-field simulation of a sphere-plane electrical contact[J].IEEE NO.2,2005:224 - 231.
[2] Yoshihiro Kawase and Hiroyuki Mori.3-D Finite Element Analysis of Electrodynamic Repulsion Forces in Stationary Electric Contacts Taking into Account Asymmetric Shape[J].IEEE NO.2,1997:1994 -1998.
[3] Yoshihiro Kawase and Hiroyuki Mori.3-D Finite Element Analysis of Repulsion Forces on.
[4] Contact Systems in Low Voltage Circuit Breakers[J].IEEE NO.3 1996:1677-1680.
[5] Tomohiro Ota,Satoshi Suzuki and Katsuhiro Hirata.Dynamic Analysis Method of Repulsion Forces On Current-Carrying Contact Using 3-D FEM[J].IEEE NO.5,2011:942 -945.
[6] 李兴文,陈德桂,刘洪武,等.触头间电动斥力的三维有限元分析[J].高压电器,2004(2):53 -55.
[7] 刘颖异,陈德桂,李兴文,等.用三维有限元方法研究影响框架断路器电动斥力的因素[J].中国电机工程学报,2005(8):63-67.
Analysis of Electric of Contact System Based on ANSYS Finite Element M ethod
HUANGWei-jie,LAN Tai-shou,LIU Xiang-jun
(Electrical Engineering and Automation College of Fuzhou University,Fuzhou 350108,China)
The electric repulsion force of relay consists of Holm force on the contacts and Lorentz force on the conductors.The safety and the stability ofmagnetic latching relay should be confirmed by the experiment in which the contacts should not be open by the repulsion force caused by the impulse current.In this paper,finite element structural analysis are used to calculate the contact radius of the relay,and then,the current density and magnetic field distribution in the various parts of the relay are calculated by the coupling field analysis to solve the electric repulsion force.Finally,the paper calculates and analyses the repulsion force in different contact pressure and short-circuit current,aswell as the affects of different parts of contact system on the repulsion force.The study will provide the foundation for the improvement of the contact system of the relay.
magnetic latching relay,electric repulsion force,contact radius,finite element analysis
TM58
B
1004-289X(2013)04-0018-05
book=24,ebook=161
2012-10-10

