大电流下的电磁能量收集技术研究

李衍川，江和

(福州大学，福州 350108)

1 引言

无线传感节点在线监测电气参数的功能，是电器智能化技术的基础。然而传感节点的供电问题是该技术的难点。长久以来，无电池供电是学者们的愿望，但无论是电流互感器取电还是谐振耦合感应电能都因为体积大、调理电路复杂而不适用于在结构紧凑的电器开关中为节点供电。随着新锐节能方案的发展，一些新的获取能量的方法得到了开发和利用，传统的方案正在发生着改变，总的来说，整个方案正慢慢朝着集成化、信息化以及智能化的方向发展［1］。其中，以压电效应为基础的振动能量收集是效率最高的一种能量获取方式。

在大电流环境下，周围存在足够的电磁能，如果能够把该部分的能量收集起来，那么将能够使低功耗节点获得电能，实现自供电的要求。传统的电磁能量收集技术是基于法拉第电磁感应原理进行的，可是磁体和分立线圈的设计是一个难点。事实上，利用磁铁在交流大电流下能够来回振动的特性，可以直接构造一个压电振子，简单方便的实现能量收集。

2 大电流下电磁能量收集的机电模型

根据安培分子电流理论，电流会产生磁场，当电流的方向改变时，磁场的方向也会改变。电流越大，磁场越强，因此大电流环境下将能产生很大的磁场并带动处于其中的磁铁振动，振动作用于压电材料时就会使其输出电压［2］。如图1所示的是一种利用电流磁场产生压电能量的模型图，它是一种悬臂梁结构，末端磁铁在电流磁场作用下带动悬臂梁和压电双晶片振动，而每个压电陶瓷上下两个极面都覆盖有厚度为100Å/1400Å的Cr/Cu复合金属膜组成上下电极，选择固有频率为50Hz的陶瓷将使输出电压达到最大。

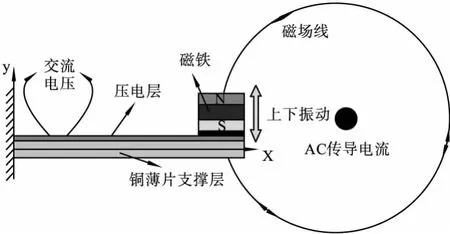
图1 悬臂梁式电磁能量收集原理图

2.1 大电流下的电磁场分析

空气中存在有应力，这样可以通过空间中电磁应力P的面积分计算得到磁场对铁磁体的作用力［3］，表达式为:

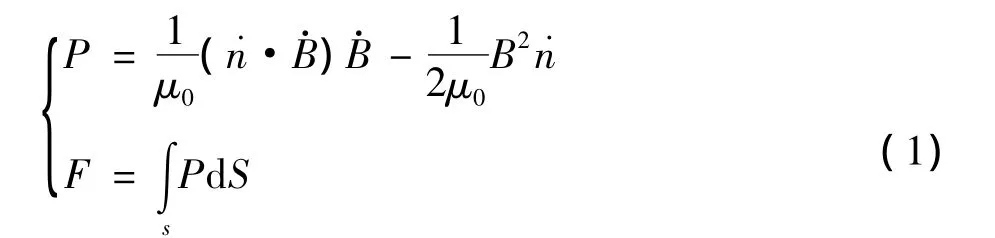
式中:μ0—空气的磁导率;

—法线方向的单位向量;

—该表面处磁感应强度向量。

利用有限元分析软件ANSOFT能够很容易的得到空气中的磁场强度和磁通密度的分布进而通过场计算器得到载流导线对铁磁物质的作用力［2］。假设长直导线与磁铁相距30mm，磁铁选用长宽高为8×8×5mm3的NdFe35永磁体，导线中通有1000A的电流，则空间中磁铁截面磁通密度云图如图2所示。

图2 磁铁截面磁通密度云图

最终，根据公式(1)进行构造ANSOFT场计算器，可以求出由传输线产生的磁场对放入其中的磁铁的力的作用为10.02N，如图3所示。

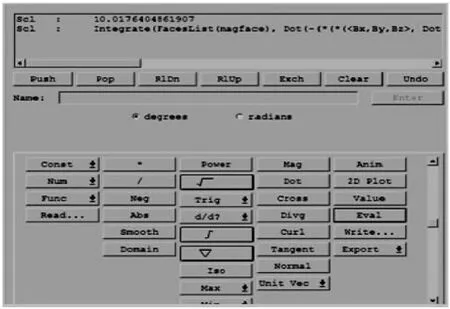
图3 ANSOFT场计算器计算磁铁电磁力结果

2.2 机电模型的压电方程

原始的压电材料呈现各向同性而整体不具有压电性，被直流电场极化后的压电材料内部电畴将趋于同一方向而呈现出压电性。当有拉伸或者压缩外力作用于压电陶瓷片上，片内的正、负束缚电荷之间的距离变小，从而导致极化强度也变小，吸附在电极上的自由电子将有一部分被释放，即在其表面将出现正负自由电荷，这就是压电效应［4］。如果悬臂梁运动的输入信号是持续的，那么机电系统就可以输出连续的电信号。梁的自由振动的微分方程为:

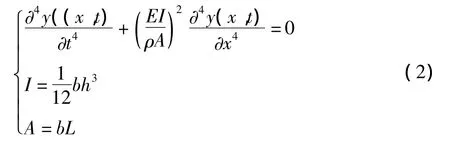
式中:y(x，t)—t时刻梁在x位置的沿y轴方向的绝对位移;

E—支撑层(铜)的弹性模量;

ρ—支撑层(铜)的密度;

I—支撑层的惯性矩;

A—压电振子的横截面积;

L—悬臂梁的长度;

b—梁的宽度;

h—梁的厚度。

该方程在Euler-Bernoulli边界条件下的一阶模态的解为:

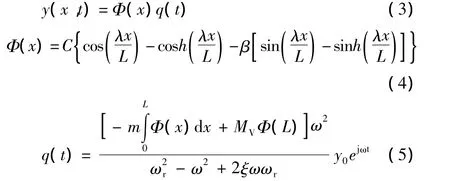
上述几个式子中:

λ—阶模态下的特征值;

C—悬臂梁的刚度;

MV—悬臂梁质量;

ωr—无阻尼振动的固有频率;

ξ—机械模态阻尼系数。

由胡克定律可知应力为:

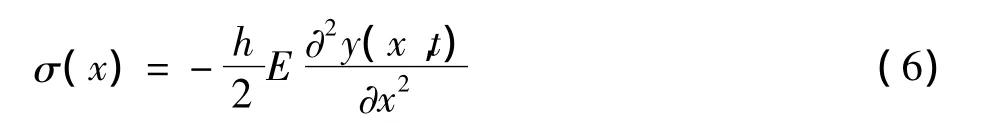
压电片粘合与梁上某处，平均输出电压可以由此处的应力与压电电压常数g33相乘获得:

3 压电效应的ANSYS仿真

ANSYS软件是融结构、热、流体、电磁、声学于一体的大型通用有限元分析软件。利用ANSYS进行压电效应分析主要是利用多物理场中结构—电分析，该模块能够模拟多种物理介质的相互作用，可以进行压电效应的静力分析、模态分析和谐响应分析［5］。

3.1 压电效应仿真步骤

压电效应的本质是结构-电的耦合分析，由前面的分析可知压电悬臂梁振动能量转换功率的大小和材料的特性、压电模式、结构尺寸、振动位移、振动频率等因素有关，利用ANSYS的耦合场分析可以对这种压电悬臂梁进行仿真，简要步骤如下:①根据图3来建立模型，需要注意的是悬臂梁的长度不宜太长，厚度则越薄越好，根据V21BL的材料特性，选取支撑层为薄铜片，长宽高尺寸为50mm×6.4mm×0.32mm，压电层尺寸为50mm ×6.4mm ×0.12mm，质量块选择 6.4mm ×6.4mm×3.2mm的铁块压电层，在该尺寸下，固有频率能接近50Hz;②压电陶瓷材料选择介电常数和耦合系数比较高的PZT-5H材料，对所涉及的材料赋值;③在单元选择时，对铜支撑层及铁块使用Solid45结构分析实体单元，对压电层则使用Solid5机电耦合单元，之后进行网格剖分;④模型中施加边界条件是悬臂梁固定端的位移为0，压电膜下极电势为0。

3.2 压电效应仿真结果

首先，求解器选择静力学分析，分析悬臂梁静态应力分布情况，以防止应力集中的地方在振动激励下发生断裂，还要防止在尖端质量块自身重力作用下，悬臂梁弯曲过大。图4则是相应的应力分布，由图可知悬臂梁的固定端是承受应力最大处，也是压电片的最佳放置处。

图4 悬臂梁承受应力分布情况

将求解器改为谐相应分析，研究压电陶瓷片产生的电压随频率的变化情况。图5就是由ANSYS的POST26后处理单元画出的压电陶瓷表面电压的变化情况，从图中可以看出在压电振子的固有频率处压电陶瓷产生的电压达到最大值。

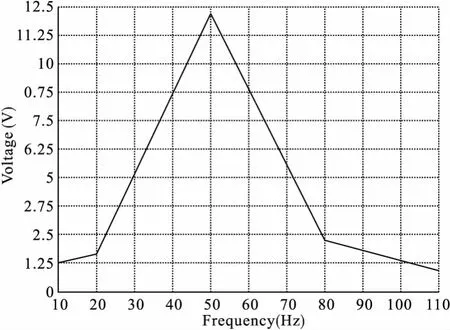
图5 电压相应与频率的关系

4 大电流下能量收集实验

为了验证压电振子在电流激励下产生电压，使用一个次级用导线短路的变压器，该变压器的额定功率为10kVA，最大能承受2500A的电流，一次侧和二次侧的变比约为95，实验时通过测量一次侧的电流大小，可以推出二次侧母排上通过的电流，现场如图6所示。

图6 压电能量收集实验现场

4.1 压电能量空载输出

分别调节电流至 200A、500A、750A、1000A，压电的输出电压如图7所示，可以看出随着电流的增大，压电输出的电压逐渐增大，并且在1000A的情况最大输出电压能够超过5V，足够驱动能量管理电路工作。另外，当电流超过750A时，压电振子的振动加剧，振动的幅度越来越大，导致了输出电压波形畸变，大电流下磁铁受到不同方向的磁场作用力所致。

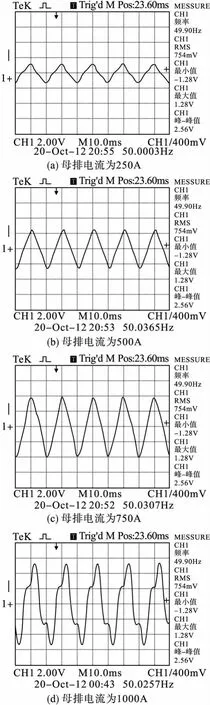
图7 不同电流下压电振子的电压输出波形图

4.2 能量管理电路调理后的压电输出

Linear公司针对压电振子能量输出特性，推出了一款适合于压电能量收集的芯片—LTC3588-1，该芯片空载情况下的静态电流为950nA，而在调成UVLO(欠压锁存)模式后静态电流只有450nA，并且输出的电压可调为3.6V。具体电路如图8所示。

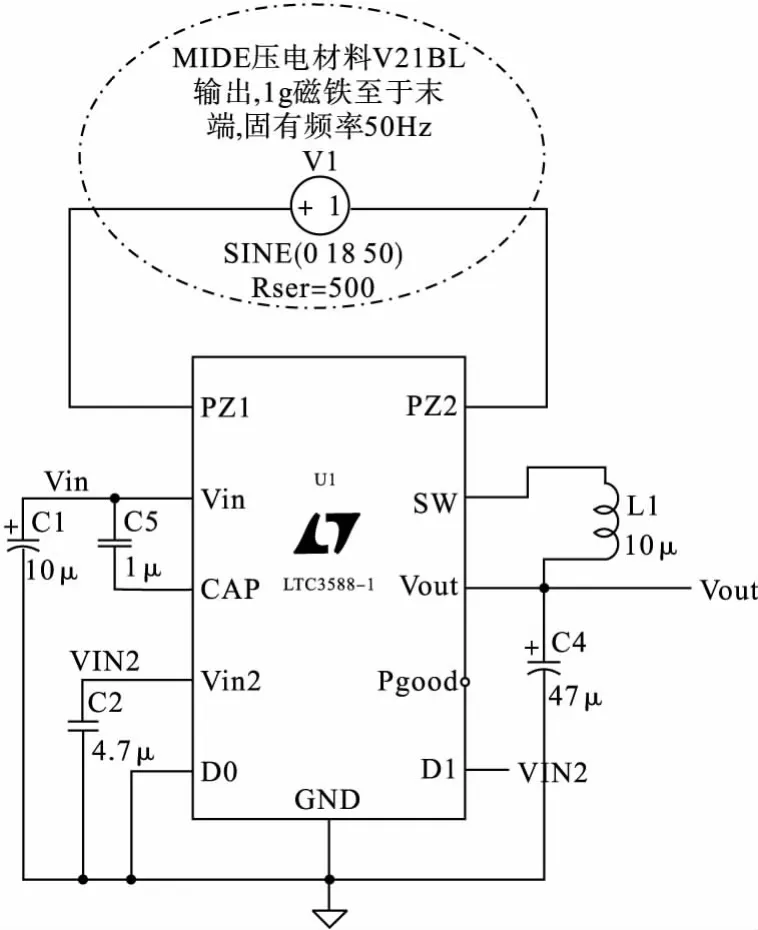
图8 LTC3588设计电路图

选用LTC3588作为压电能量管理时，无需附加的保护电路，应用起来非常方便。图9是振动激励下的压电输出和经过LTC3588调理后的波形图，在外加电流磁场作用下当电压超过4V时，就能使LTC3588-1电路输出一个稳定的3.3V电压，而其功率的大小由实际振动的强度决定。

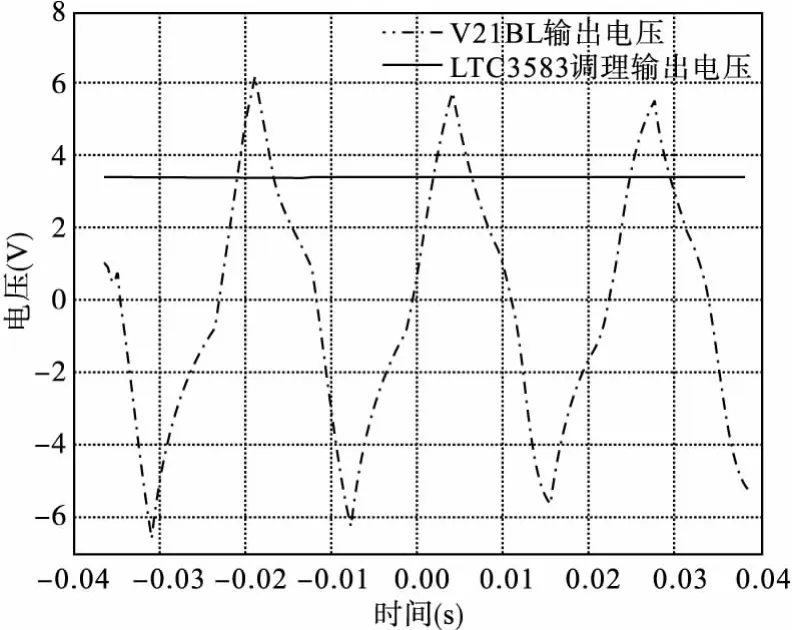
图9 能量管理电路输入输出电压波形

5 结论

交流大电流下能够产生交变的磁场，从而带动磁铁来回振动，压电材料能够将振动能转换成电能，使用LTC3588-1调理后能转换成可用的直流小电压。实验证明，将调理后的电路给超级电容充电，充电电流最大可达400μA。压电振子能持续提供充电电流说明了大电流下电磁能量收集的可行性。

［1］ 沙山克.普里亚，丹尼尔.茵曼.能量收集技术［M］.南京:东南大学出版社，2011.

［2］ Roundy S，Wright PK.A Piezoelectric Vibration Based Generator for Wireless Electronics［J］.Smart Materials and Structures，2004，13(5):1131-1142.

［3］ Zhu M，Judd M，Moore P.Energy Harvesting Technique for Powering Autonomous Sensors within Substations［J］.Proc.1st International Conference on Sustainable Power Generation and Supply，2009，24(13):465-468.

［4］ 佟刚.压电发电及自供能装置的研究［D］.吉林大学，2007.

［5］ 王青萍.压电能量收集器的有限元仿真与分析［J］.湖北第二师范学院学报，2011，28(3):38-40.