基于特征模型的力矩受限卫星三轴姿态控制*

现代航天器的复杂任务常常要求卫星能够进行大角度快速机动，而有限的燃料或执行机构能力常常造成卫星控制输入受限.很多实际的物理系统都存在饱和问题，饱和严重时直接导致系统性能下降，有的甚至系统不稳定.饱和控制一直都是控制理论及应用中的热点问题，这个问题已经有半个多世纪的研究历史.在上世纪八九十年代中，很多研究人员已经提出了比较完备的研究理论.在连续系统中，Sontag和Sussmann[1]很早指出只有在开环极点中没有正实部根的稳定线性系统才能在有界输入控制下达到全局渐近稳定.Fuller[2]和Sussmann等[3]也分别论证了对于一个n阶饱和积分系统，只要n≥3，就无法通过设计线性控制律来使系统全局渐近稳定.理论研究说明对于一个输入饱和线性系统，只有系统所有极点都在左半闭平面内才能够控制达到全局渐近稳定，而且，除了极少数的简单情况外通常都要用到非线性控制律.Lin和Saberi[4-7]提出了一种低增益反馈的方法，这种方法通过设计线性反馈控制律来使系统达到半全局指数稳定.这类控制器通过解一个与对象相关的Riccati方程来决定控制器增益矩阵，从而使输入饱和系统稳定.这种方法不仅设计简单，而且大幅削弱了由饱和所导致的性能下降的影响.但是这种方法也有它的局限性，主要是对一些复杂的、甚至对象本身是非线性的系统，当无法用状态方程方便地描述系统时，应用这个方法就会遇到困难.而对于三轴卫星姿态控制就面临控制非线性对象这样一个难题，这时候这种低增益方法无法直接应用.

特征模型是吴宏鑫院士在上世纪八十年代提出的一种新的模型描述方法[8].随着科学技术和生产发展，被控对象的结构越来越复杂，精确动力学建模也越来越难，而且控制器的设计希望在满足性能指标的要求下越简单越好，以利于低阶控制器的设计.特征建模能够根据对象动力学特征、环境特征和控制性能要求相结合来建模.这种建模方法的特点是：(1)在同样的输入控制下，对象特征模型和实际对象在输出上是等价的(即在动态过程中能保持在允许的输出误差范围内)，在稳定情况下，输出是等价的；(2)特征模型的形式和阶次除考虑对象特征外，主要取决于控制性能要求；(3)特征模型建立的形式应比原对象的动力学方程简单，易于控制器设计，工程实现容易、方便；(4)特征建模与高阶系统的降阶模型不同，它是把高阶模型有关信息都压缩到几个特征参量之中，并不丢失信息.通过结合特征模型和低增益饱和控制方法可以有效地解决低增益饱和控制方法的不足之处，扩展了这种方法的应用范围，本文以一个卫星对象的三轴姿态机动控制为例说明应用方法，并仿真验证方法的有效性.

1 挠性卫星动力学模型及特征建模

三轴卫星姿态控制对象为非线性系统，为了应用低增益方法进行饱和控制器设计，首先建立其相应的特征模型.根据特征建模理论，特征模型和原对象动力学模型具有在相同控制输入下输出等价的特点，因此可以将低增益方法应用在二阶差分方程形式的对象特征模型上.特征模型的典型形式是以一个二阶时变差分方程描述[8]：

y(k+1)=f1(k)y(k)+f2(k)y(k-1)+g0(k)u(k)+g1(k)u(k-1)

(1)

根据这种模型描述方法的特点及结构形式，可以进一步设计简单的控制器，而且通过文献[9]证明了控制器对原复杂系统有效.

三轴稳定的刚体卫星动力学模型可以描述为[10]

(2)

定义卫星三轴欧拉姿态角X=[φθψ]T，其中φ，θ，ψ分别为航天器的滚动、俯仰和偏航角.运动学采用3-2-1转序，得到姿态运动学关系

(3)

根据文献[8]，建立以上三输入三输出线性定常系统的特征模型.

对式(3)两边求导

(4)

将式(4)代入式(2)并且左乘ST，并记

(5)

整理得三轴欧拉姿态角与力矩关系

(6)

式中M为正定矩阵.

根据特征建模机理，在系统采样时间Ts情况下对式(6)进行欧拉近似离散

式(6)所对应特征模型

X(k)=f1(k)X(k-1)+f2(k)X(k-2)+

g0(k)T(k-1)+Δd

(7)

于是式(7)可变为

X(k)=f1(k)X(k-1)+f2(k)X(k-2)+g0(k)T(k-1)

(8)

2 低增益饱和控制方法

根据Lin[7]的低增益控制器设计理论，对于一个输入饱和的单输入单输出线性系统

x(k+1)=Ax(k)+Bσ(u(k))

(9)

y(k)=Cx(k)

(10)

当饱和函数σ(u)满足下列条件：

(1)当s≠0时，sσ(s)>0而且σ(0)=0；

(3)饱和函数是局部Lipschitz的.

而且系统矩阵满足下列条件:

(1)矩阵A的特征根全都在单位圆内或圆上；

(2)矩阵(A,B)是可控的；

(3)矩阵(A,C)是可观测的.

那么可以通过设计线性反馈控制器使得系统半全局指数稳定.

存在唯一的正定矩阵K使得下面代数Riccati方程成立

ATK(ε)A-K(ε)-ATK(ε)B(BTK(ε)B+1)-1BTK(ε)A+εE=0

(11)

而且K-ATKB(BTKB+ 1)-1BTKA是渐近稳定的，其中ε∈(0,1].

令控制律u=-(BTKB+1)-1BTKAx(k)，则式(9)和(10)描述的系统将半全局指数稳定.

根据文献[7]中方法确定ε的范围.首先给定一有界区域W⊂Rn，根据文献[7]中引理3.2选择c满足条件

c≥xTK(ε)xε∈(0,1],x∈W

(12)

再根据Lyapunov稳定性原理确定ε*，ε*是使下列不等式组成立的最大ε值.

(13)

则对任意ε∈(0,ε*)所设计控制律都能使得系统吸引域包含区域W，即达到半全局指数稳定.

3 基于特征模型的低增益饱和控制器设计

根据文献[8]理论，待确定的特征模型参数形式可具体为

根据已知条件及推导过程求解部分参数范围为

a11(k)∈(1.997,2)，a12(k)∈(1.99987,2)，

a13(k)∈(1.9985,2)，a21(k)∈(-1,-0.997)，

a22(k)∈(-1,-0.99987)，a23(k)∈(-1,-0.9985)，

b11(k)∈(3.118×10-8,3.167×10-8)，

b22(k)∈(2.322×10-8,2.685×10-8)，

b33(k)∈(1.642×10-8,3.786×10-8).

在上述各值的范围内取中间值附近一定值，可以将所得到的二阶差分方程分别近似写成滚动、俯仰、偏航三轴对应状态方程形式

(14)

(15)

(16)

求解下面的Riccati方程：

(17)

(18)

将所得到的控制律分别代入各轴饱和函数即可.

4 数学仿真

卫星滚动、俯仰、偏航三轴各自机动轨迹为(单位(°))

(19)

(20)

(21)

其中t为仿真时间,采样时间Ts=0.01s.控制输入饱和函数形式如下(单位N·m):

(22)

(23)

(24)

这是常见的饱和环节函数，显然符合第二部分关于饱和函数的基本假设.

当没有输入受限时，采用未加饱和控制的普通控制方法控制系统效果如图1和图2所示.

当饱和环节存在时，若不用低增益方法控制，系统将不再收敛，如图3和图4所示.

通过本文所设计的基于特征模型的低增益控制方法，在饱和环节存在时，系统达到稳定，而且控制效果很好，如图5和图6所示.

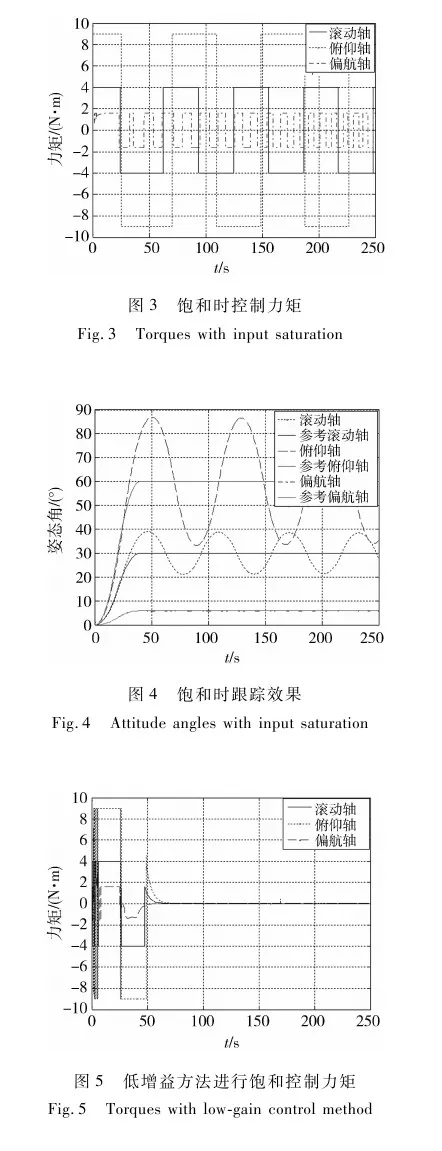
图6 低增益方法进行饱和控制跟踪效果

5 结束语

本文建立三轴卫星的动力学模型并推导了特征模型，分析推导了特征模型参数范围。给出了低增益饱和控制方法，并设计了基于特征模型的低增益饱和控制器，通过设计的控制器使输入力矩饱和的卫星三轴姿态机动控制收敛，仿真验证了控制器有效。这种基于特征模型的控制器设计方法拓展了低增益饱和控制方法的适用范围，有效解决了一类非线性对象的饱和控制问题。

参 考 文 献

[1]Sontag E D, Sussmann H J. Nonlinear output feedback design for linear systems with saturating controls[C]. The 29thIEEE Conference on IEEE,Honolulu，1990

[2]Fuller A T. In-the-large stability of relay and saturating control systems with linear controllers[J]. International Journal of Control, 1969,11(4):457-480

[3]Sussmann H J, Yang Y. On the stabilizability of multiple integrators by means of bounded feedback controls[C]. The 30thIEEE Conference, Brighton, 1991

[4]Lin Z L, Saberi A. Semi-global exponential stabilization of linear systems subject to “input saturation” via linear feedbacks[J]. Systems and Control Letters, 1993, 21(3):225-239

[5]Lin Z L. Low gain feedback[M].London: Springer,1999

[6]Saberi A, Lin Z, Teel A. Control of linear systems with saturating actuators[J].Automatic Control, 1996, 41(3):368-378

[7]Lin Z L, Saberi A, Stoorvogel A A. Semi-global stabilization of linear discrete-time systems subject to input

saturation via linear feedback-an ARE-based approach[J]. Automactic Control,1996,41(8):1203-1207

[8]吴宏鑫. 全系数自适应控制理论及其应用[M]. 北京: 国防工业出版社, 1990

[9]吴宏鑫,胡军,解永春. 基于特征模型的智能自适应控制[M]. 北京:中国科学技术出版社, 2009

[10]雷拥军,谈树萍,刘一武.一种航天器姿态快速机动及稳定控制方法[J]. 中国空间科学技术,2010,30(5):48-53

Lei Y J,Tan S P,Liu Y W.Spacecraft control method for fast attitude maneuver and stabilization[J]. Chinese Space Science and Technology, 2010,30(5):48-53