游憩价值TCM评估的概念偏差分析

游 武，许丽忠，张江山

(福建师范大学环境科学与工程学院，福建福州350007)

在环境资源价值评估中，旅行费用法(travel cost method，TCM)是最为流行的游憩资源价值评估方法之一．TCM是由美国学者Clawson等人于1959年提出的，被广泛应用于各种公共商品、游憩活动的价值评估［1－4］．TCM技术在理论上已不断趋于成熟，衍生出分区旅行费用法(ZTCM)和个人旅行费用法(ITCM)等．国内近几年公开发表的TCM研究案例不断增加［5－30］，对多目的地偏差、时间机会成本偏差、样本偏差以及回归分析计算偏差等研究已有报道［31］．而对其原理或概念理解失误所导致的偏差(简称概念偏差)方面的研究鲜见报道．本文基于分区旅行费用法研究游憩价值TCM评估的概念偏差．

1 旅游需求曲线和消费者剩余曲线

TCM方法的核心是通过旅行费用与旅游人次关系构建虚拟的消费者剩余曲线．户外娱乐场所或自然景区的游憩价值为消费者支出与消费者剩余之和．消费者支出可采用费用支出等方法求得，而消费者剩余则是通过消费者剩余曲线求得．在求解消费者剩余时，TCM技术实际上运用了2条不同定义下的需求曲线:一条是旅游需求曲线(图1)，表示不同旅行费用(或门票价格)下旅游人次的变化;另一条则是根据影子价格理论构建的、虚拟的“增加价格－需求”曲线，即消费者剩余曲线(图2)．2条曲线形式相似，含义却不同．如果混淆了这2条曲线，会导致最终计算结果出现偏差．

2 TCM概念偏差分析

2．1 旅游需求曲线含义的偏差

假设游客到某一户外娱乐场所或自然景区游览的消费是享受或利用该自然资源的隐含价格，价格的提高必然导致需求(旅游人次)的减少，将不同旅游价格下的旅游人次点连接起来就构成了旅游需求曲线(图1)．对于游憩资源(旅游区)而言，它的旅游规模随着门票费用的提高而减小，此时的旅游费用即为门票费用(图1)．图1中P点系指当前的门票价格，此时需求曲线下的面积(P*AOB)为该游憩资源的总旅游价值，等于游客对该资源的支付意愿，即在目前门票价格下各出游小区消费者旅游的实际支出(POBP*)与其消费该商品或服务所获得的消费者剩余(APP*)之和．对于各出游小区而言，虽然其旅游实际支出各不相等，但其中门票支出部分相同，因此可使用门票价格作为各出游小区的统一表征，形成一条以该旅游区为研究对象、以统一的门票为不同旅游费用表征的“价格(门票)－旅行规模”的需求曲线(旅游需求曲线)．但这条旅游需求曲线只是一条具有象征意义的“价格－需求”曲线，图1上需求曲线所围出的面积并不具有数学意义上的价值概念，即POBP*面积≠∑价格×需求，因为它的横坐标(旅游人次)、纵坐标(旅游费用)均是一个复合概念．横坐标(旅游人次)是具有不同社会属性的游客人数之和(他们的支出并不相同)，这些游客人数随价格的变化遵循不同规律．而纵坐标(门票)只是一个象征性指标，如对于出游小区Ⅰ，门票价格(P)可能对应于旅行费用(300美元)，而对于出游小区Ⅱ，P对应的旅行费用则可能仅为50美元．

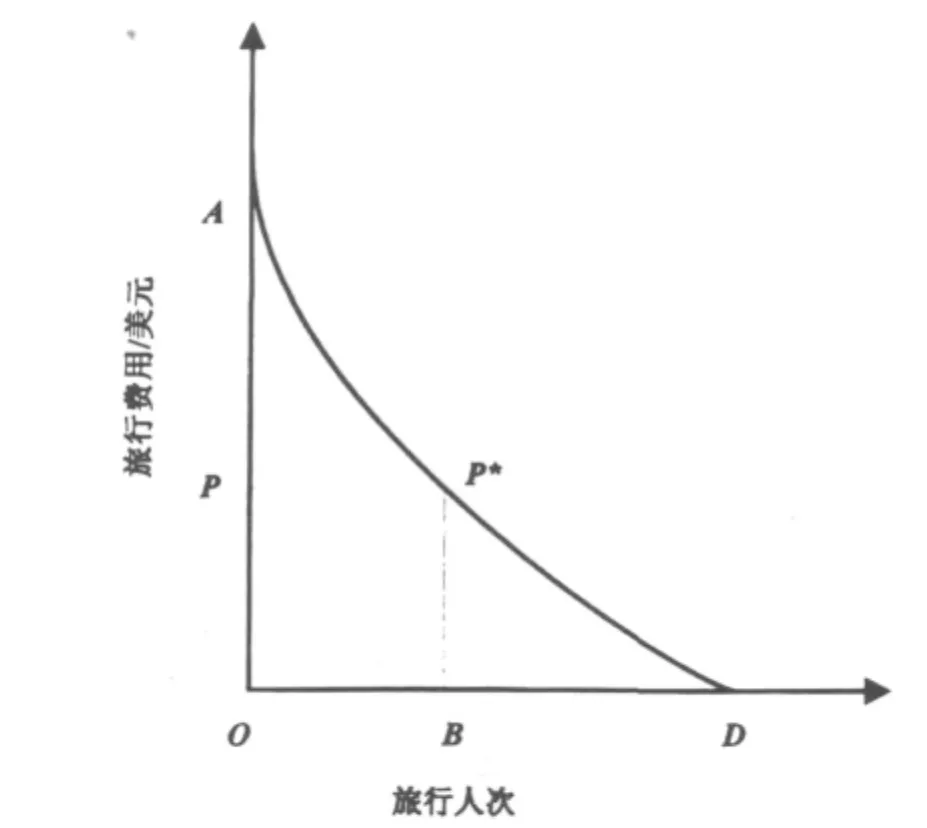
图1 旅游需求曲线及游憩价值构成Fig．1 Tourism demand curve and recreation cost constitutions

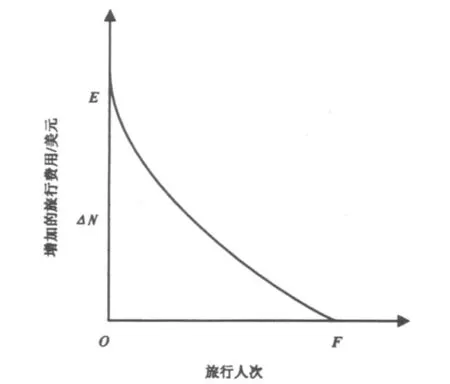
图2 消费者剩余曲线Fig．2 The consumer surplus curve

对于某一出游小区而言，该需求曲线表示该出游小区(客源地)对该游憩资源的需求随着旅行费用的增加而降低，此时其旅游费用包含门票、直接交通费及其它必不可少的费用．将同一客源地游客必不可少、基本相同的支出费用定义为硬支出．需求曲线下的面积表示该出游小区享受该游憩资源所得到的旅游价值，其旅游价值依然由消费者旅游实际支出(POBP*)和消费者剩余(APP*)构成．但与研究对象主体为旅游区不同，它是一条完整的“价格－需求”曲线，横轴表示具有相同社会属性的游客，纵轴表示他们相同的硬支出，此时图形上需求曲线所围出的面积即POBP*面积=∑价格×需求．这是以需求曲线的主体为客源区与以需求曲线的主体为旅游区的本质区别．

旅游区的价值是由各个客源地共同构成的．不同客源地对该旅游区的需求曲线不同，相应地该客源地的旅游区游憩价值也就不同．将所有客源区的需求曲线叠加则可得到总需求曲线，所有客源区的价值总和则为该游憩资源的价值．各客源地旅游区游憩价值代数和即为该旅游区的游憩总价值，各小区的消费者支出之和即为旅游区总消费者支出，各小区的消费者剩余之和即为该旅游区总消费者剩余．需求曲线的叠加则复杂得多．由于旅游区每一门票价格均对应于每一客源区某一旅行费用，也就对应于此旅行费用下的旅游人次，将各客源区相应的旅游人次相加，即为旅游区此种门票价格下的旅游人次．如此依次求出不同门票价格下的旅游区旅游人次，将点依次相连，即可得旅游区的旅游需求曲线，这样就将各客源区的需求曲线叠加为该旅游区的旅游需求曲线．

2．2 消费者剩余曲线含义的偏差

消费者剩余曲线是TCM计算的核心．消费者剩余曲线的构建是基于旅游区需求曲线的构建．消费者剩余为未实现、潜在的价值量．下面举一个简单的例子说明消费者剩余在旅游资源经济中是如何体现的．

假设旅游率与旅游费用有一定的相关性，当旅游费用为1美元时，旅游率为0．5，当旅游费用为2美元时，旅游率为0．2，当旅游费用为3美元时，旅游率为0．1，当旅游费用为4美元时，没有人旅游，旅游率为0．旅行总费用为门票价格与距离成本之和，假定有某区域A人口数为1000人，到旅游区的距离成本为1美元．当门票价格为0即旅行总费用为1美元时，A区共有500人去旅游，此时消费者的实际支出为500美元．在这500名游客中有200名游客，当旅行总费用增加1美元即总费用为2美元时仍将去游览，此时有200美元的价值没有显现出来;而这200名游客中又有100名游客在旅行总费用再增加1美元，即总费用为3美元时还将去游览，即还有潜在的100美元的价值没有显现出来;当旅行总费用再增加1美元，即总费用为4美元时则没有人去游览．对A区的游客而言，当旅行总费用为1美元时，旅游区实现了500美元的价值(消费者实际支出)，同时还有(200美元+100美元)300美元的价值没有显现出来．因此可以认为对于区域A的游客，当旅行总费用为1美元，即门票价格为0时，旅游区的总价值为800美元，其中500美元已实现，尚有300美元价值未实现．这未实现的300美元即是消费者剩余(表1)．

表1 旅游区客源A区的游憩价值与消费者剩余Table 1 The tourism value and tourism consumer surplus of A Zone of tourist source

如果将旅行实际费用作为影子价格，当影子价格增加，即实际旅行费用增加时，不同旅游费用增加量下旅游人次的变化构建了消费者剩余曲线．离评价地点越远的用户，其消费者剩余越小;而离评价地点最近的用户，其消费者剩余最大．

消费者剩余实际上就是在某一实际价格之上的需求曲线与坐标轴围成的面积(图1中区域APP*)，也可以说消费者剩余曲线是旅游需求曲线的一部分．消费者剩余曲线与旅游需求曲线的外形十分相似，但有差别，即旅游需求曲线的纵坐标为旅行费用(或者为门票价格)，而消费者剩余曲线的纵坐标为增加的旅行费用．增加的旅行费用用一个微小的变化△N表示，则其对应的消费者剩余为图2中的矩形面积，总的消费者剩余就是图2中消费者剩余曲线下围成的面积(EOF)．该消费者剩余(EOF面积)是对图1中区域APP*进行变换后得到的．

因此当消费者剩余曲线构建的主体为各客源区游客时，曲线下面积表示的是该小区的消费者剩余，将各小区的消费者剩余累加则为游憩资源总消费者剩余．当研究主体为游憩资源时，此时增加的费用即为门票价格的增量(门票对旅游规模的影响与旅行交通费用和机会成本相同)，则该曲线的积分即表示该游憩资源总的消费者剩余．因此在实际操作中，对消费者剩余的计算通常可以采用2种方法．一是构建每一出游小区的消费者剩余曲线，求出每一出游小区的消费者剩余，通过求和得到旅游区的总消费者剩余;二是将各小区的消费者剩余曲线叠加起来，得到该游憩资源的总消费者剩余曲线，由此求出总消费者剩余．目前这2种方法在我国研究案例中都有被采用．但第1种方法需要对n个小区的n条曲线进行积分，而第2种方法仅需构建1条曲线，计算1次积分．因此目前第2种方法更常用．

2．3 消费者剩余计算中积分上、下限确定的4种错误分析

消费者剩余的计算可以转换为对消费者剩余曲线的积分计算．由于消费者剩余曲线表示增加费用与需求之间的关系．积分的下限为0(有时也可将起点定在接近于0的数值);而积分上限为增加费用的最大值，即费用增加幅度达到该水平时，旅游人次将降为0．用Pm表示最大追加费用，则消费者剩余价值可采用如下式子计算:

式中，CS表示旅游区总消费者剩余，Y(x)表示增加费用与旅游人次的函数关系．积分的上下限均为费用的增加量，两者数据应相匹配．由于消费者剩余曲线同时也是当前价格之上的旅游需求曲线，因此当旅游需求曲线的主体为各客源区时，也可以利用旅游需求曲线求消费者剩余．由于消费者剩余曲线是当前价格之上的旅游需求曲线，即消费者剩余曲线的起点为当前价格，而终点为该客源区旅游人次为0时的价格．用数学式表达如下:

式中，CSi表示第i个客源区的消费者剩余，Pl表示该客源区至旅游区的当前价格，Ph表示该客源区至旅游区的最高价格，n表示客源区的数量．

2．3．1 根据出游小区距离确定积分上、下限 将离游憩资源最近的出游小区的旅行费用(最低旅行费用)作为积分的下限，而将离游憩资源最远的出游小区的旅行费用(最高旅行费用)作为积分的上限．

采用这种处理方法，研究者无法清晰地表达其计算所采用的是旅游需求曲线还是消费者剩余曲线，也就是说，不明确它的计算主体是旅游区还是各客源区．

研究案例分析结果表明:旅游率的大小不仅与各小区的旅行支出有关，同时还与各出游小区收入水平、旅游时间、教育水平等因素有关，同一旅行费用对某一出游小区可以接受，而对于另一出游小区而言可能会导致出游率降为0;同理，某一旅行费用可能会使某小区的旅游率为0，并不意味着其他出游小区的旅游率也为零．也就是说最高费用对旅游需求曲线、消费者剩余曲线均不具有特殊意义，它并不对应于图1中的A点或图2中的E点．

旅游率与旅行费用关系的构建通常需要以下几步．首先应根据调查数据确定旅游率的相关因子，即旅行费用、收入水平、旅行时间等．二是依据一定的统计分析手段建立旅游率与这些相关因子的回归曲线．该回归方程以相关因子旅行费用、收入水平、旅行时间等为自变量，以旅游率为因变量．三是简化回归方程．因为对于每一小区，在旅行时间、收入水平一定的情况下，可仅考虑旅游率与旅行费用的关系．由于各出游小区的旅游时间、收入水平等并不相同，可以将各小区不同的旅游时间、收入水平等代入步骤二的回归方程，得出不同出游小区的旅游率与旅行费用的关系式．N个小区就有N个式子，这些式子形式相同，但参数(系数)不同．因此对不同区域来说，对同一种价格的接受能力是不同的．采用这种数据处理方式的缺点是忽略了各个出游小区游客属性的差异．

2．3．2 以旅行费用的差值作为积分限值 将积分下限定为0，而将最高旅行费用与最低旅行费用之差作为积分上限．通过消费者剩余曲线来求解消费者剩余．消费者剩余曲线表示增加费用与需求的关系．当消费者剩余曲线的主体为旅游区时，消费者剩余曲线实际上也是一条复合曲线，而最高旅行费用和最低旅行费用来自不同的客源地，两者并无联系．对于复合的消费者剩余曲线来说，最高旅行费用与最低旅行费用之差也就没有特定的含义，它并不表示旅游区旅游人次降为0时的门票增加幅度．同时由于最高旅行费用与计算得出的最大旅行费用不同，因此将最高旅行费用与最低旅行费用之差作为积分上限是错误的．

2．3．3 以旅行费用极限值作为积分限值 以目前最低旅行费用为积分下限，以根据消费者剩余曲线计算出的旅行费用最大增量作为积分上限．采用该计算方法导致的计算偏差表现为积分上下限不匹配．由于在构建消费者剩余曲线时，旅行费用的增加等同于门票价格的增加，因此消费者剩余曲线的纵坐标(或横坐标)只能是门票的增加额(即追加费用)．如果取现有的旅行费用作为起点，取最大追加费用为上限(消费者剩余曲线上的点)，对消费者剩余曲线进行积分得到的数据不匹配．

2．3．4 以门票价格作为积分限值 即将目前门票价格作为积分下限，将从旅游需求曲线中求出的最高门票价格(此时旅游区旅游人次为0)作为积分的上限．该方法的研究主体为旅游区，此时旅游区的旅游需求曲线是一条象征性的“价格－需求”曲线，旅游区的游憩价值并不能从旅游需求曲线中直接求得，需要将它分解成消费者支出与消费者剩余两部分．由于消费者剩余曲线是旅游需求曲线在现行(门票)价格之上的那部分曲线，将旅游需求曲线在现行(门票)价格之上的那部分曲线截取即可得到消费者剩余曲线，旅游需求曲线上当前的门票价格对应于消费者剩余曲线上的起点O，旅游需求曲线上最高门票价格对应于消费者剩余曲线上的终点E(最大增加费用)，因此消费者曲线与旅游需求曲线在方程表达方式上大致相同，但2条曲线表示的含义不同，同时2条曲线的截距可能不同．如果将最低旅行费用作为积分下限，将从旅游需求曲线中求出的最大旅行费用作为积分的上限，那么得到的方程式则是旅游需求曲线而不是消费者剩余曲线．将旅游需求曲线在上述范围内积分得到的数值与消费者剩余曲线上下限内积分的数值相同．但是由于这条旅游需求曲线是一条复合曲线，其与坐标轴之间围成的面积并不表示“∑价格×需求”，因此这种计算方法不够准确．

当研究主体为各客源地时，对各客源地的游客来说，他们被视为具有相同属性的同一个整体，费用增加就是旅行费用的提升，因此对这一群体而言，其旅游需求曲线与坐标轴围出的面积在数值上等于其相对应的价值量，因此可利用旅游需求曲线求解其消费者剩余，也就是说，可以利用旅游需求曲线现行旅游价格以上至最大可接受价格(即旅游人次为0时价格)与坐标轴围出的面积求出该客源地游客的剩余价值．但对于每一个客源地来说，其旅游需求曲线不同，现行旅游价格不同(不都等于最低旅行费用)，其最大可接受价格也不同(不都等于最大旅行费用)，即其积分范围均不同．将各客源地的消费者剩余价值相加得到总剩余价值．

2．4 门票价格为0时的游憩价值

对于门票价格为0的游憩资源，国内外有些学者仅用消费者剩余代替游憩价值．

对于门票价格为0的游憩资源，当研究主体为该旅游区时，其旅游需求曲线中P点对应的纵坐标为0，消费者实际支出部分在图中被隐藏，因此，从图1仅可得出“消费者支出=0，游憩价值=消费者剩余”的结论．但是该旅游需求曲线实际上是一条复合曲线，是多条客源地的旅游需求曲线的叠加，当该曲线转化为以各出游小区为研究主体，将该曲线还原为各客源地的需求曲线时，消费者实际支出便显现出来．计算结果表明，即便对于门票价格为0的游憩资源，消费者实际支出也是不可忽视的．只有消费者支出与消费者剩余之和才是完整的“消费者自愿支出”，才是所求的旅游资源总游憩价值．

3 小结

本文首先辨析了旅游需求曲线和消费者剩余曲线的内在关联与异同，揭示了旅游需求曲线2种层面上的含义，分析了消费者剩余积分计算时积分上、下限确定的4种错误．基于旅游需求曲线的分析，指出即便门票价格为0，其消费者支出仍然存在，游憩价值不仅仅是消费者剩余．

［1］ZADERSEN M，TOL R S J．A meta-analysis of forest recreation values in Europe［J］．Journal of Forest Economics，2009，15(1):109－130．

［2］FLEMING C M，COOK A．The recreational value of Lake McKenzie，Fraser Island:anapplication of the travel cost method［J］．Tourism Management，2008，29(6):1197 －1205．

［3］GURLUK S，REHBER E．A travel cost study to estimate recreational value for a bird refuge at Lake Manyas，Turkey［J］．Journal of Environmental Management，2008，88(4):1350 －1360．

［4］STARBUCK M，ALEXANDER S J，BERRENS R P．Valuing special forest products harvesting:a two-step travel cost recreation demand analysis［J］．Journal of Forest Economics，2004，10(1):37 － 53．

［5］刘亚萍，潘晓芳，钟秋平，等．生态旅游区自然环境的游憩价值——运用条件价值评价法和旅行费用法对武陵源风景区进行实证分析［J］．生态学报，2006，26(11):3765 －3774．

［6］许丽忠，张江山，王菲凤，等．熵权多目的地TCM模型及其在游憩资源旅游价值评估中的应用——以武夷山景区为例［J］．自然资源学报，2007，22(1):28 －36．

［7］詹丽，杨昌明，李江风．用改进的旅行费用法评估文化旅游资源的经济价值——以湖北省博物馆为例［J］．软科学，2005，19(5):94 －96．

［8］谢贤政，马中．应用旅行费用法评估黄山风景区游憩价值［J］．资源科学，2006，28(3):128－136．

［9］欧阳勋志，廖为明，黄晓全．婺源县森林景观游憩价值的经济评价［J］．地域研究与开发，2006，25(1):78－82．

［10］王洪翠，吴承祯，洪伟，等．武夷山风景名胜区游憩服务功能价值评估［J］．福建农林大学学报:哲学社会科学版，2007，10(2):60－63．

［11］王菊，马若为，侯春燕，等．伪皇宫博物院游憩效益评价研究［J］．环境与可持续发展，2006(5):14－17．

［12］范繁荣．宁化牙梳山自然保护区森林生态系统服务功能及价值评估［J］．福建农林大学学报:自然科学版，2006，35(5):283－287．

［13］乔光华，王海春，韩国栋，等．达里诺尔国家级自然保护区游憩服务功能价值评估［J］．绿色中国，2005(12):53－55．

［14］聂金荣，钟全林，戴卓．井冈山市天然林游憩价值核算［J］．生态经济，2005(2):80－85．

［15］胡淑萍，李卫忠，余燕玲，等．基于TCM的太白山森林公园游憩效益评估［J］．西北林学院学报，2005，20(2):171－174．

［16］张茵，蔡运龙．基于分区的多目的地TCM模型及其在游憩资源价值评估中的应用——以九寨沟自然保护区为例［J］．自然资源学报，2004，19(5):651 －661．

［17］郭剑英，王乃昂．旅游资源的旅游价值评估——以敦煌为例［J］．自然资源学报，2004，19(6):811－817．

［18］孙根年，孙建平，吕艳，等．秦岭北坡森林公园游憩价值测评［J］．陕西师范大学学报:自然科学版，2004，32(1):116－120．

［19］李巍，李文军．用改进的旅行费用法评估九寨沟的游憩价值［J］．北京大学学报:自然科学版，2003，39(4):548－555．

［20］吴章文，罗艳菊．鼎湖山风景区森林游憩价值评价研究［J］．林业经济，2003(5):26－21．

［21］陈伟琪，刘岩，洪华生，等．厦门岛东部海岸旅游娱乐价值的评估［J］．厦门大学学报:自然科学版，2001，40(4):914－921．

［22］陈浮，张婕．旅游价值货币化核算研究——九寨沟案例分析［J］．南京大学学报:自然科学版，2001，37(3):296－302．

［23］亢新刚，陈光清，刘建国．芦芽山自然保护区森林资源价值评估［J］．北京林业大学学报，2001，23(3):60－63．

［24］曹辉，兰思仁．福州国家森林公园森林景观游憩效益的评价［J］．林业经济问题，2001，21(5):43－44．

［25］靳乐山．用旅行费用法评价圆明园的环境服务价值［J］．环境保护，1999(4):31－33．

［26］薛达元，包浩生．长白山自然保护区生物多样性旅游价值评估研究［J］．自然资源学报，1999，14(2):140－145．

［27］程弘，费乙，赵纯烈，等．兴隆山国家级自然保护区森林资源游憩价值评估［J］．甘肃林业科技，1997(4):40－44．

［28］艾运盛，高岚，邱俊齐．武夷山风景名胜区游憩效益的评价［J］．北京林业大学学报，1996，18(3):89－97．

［29］吴楚材，邓金阳，李世东．张家界国家森林公园游憩效益经济评价的研究［J］．林业科学，1992，28(5):423－430．

［30］孙春杰．我国生态旅游地环境价值分析研究［D］．上海:上海交通大学，2001．

［31］周慧滨，左旦平．旅行成本法在我国应用中存在的几个问题［J］．自然资源学报，2006，21(3):489－499．