BP神经网络在基坑周边地表短期沉降预测中的应用

徐鑫鑫，苏华友，张春萍

(西南科技大学环境与资源学院，四川 绵阳 621010)

引言

随着地铁项目在我国的迅速发展，地铁隧道开挖引起的地表沉降越来越影响人们的日常生活，在城市中心的地表沉降容易导致附近建筑物的倾斜，隧道上方管线变形破坏等问题。目前，国内外对地表沉降规律的研究尚不十分成熟。工程中较常用的方法是根据施工动态的监测数据对沉降值进行推算，以期提高预测的精度。然而，对于饱和土而言，许多观测实例表明，指数曲线法预测的结果往往偏小，而双曲线预测的结果又往往偏大［1］。另外，灰色理论也受限于非等时距，以及观测值累加生成时常不具有指数规律等情况［2-3］。目前，随着计算机技术的普遍应用，结合计算机软件研究地表沉降规律已成为趋势，其将大大提升研究效率，有效提高预测精度。本文将结合Matlab软件，通过建立BP神经网络，对苏州地铁2号线某工程周边地表的沉降进行短期预测。

1 BP神经网络的结构及算法

BP网络是多层前馈型神经网络，可以实现从输入到输出的任意非线性映射。典型的BP网络拓扑结构如图1所示，一般具有3层，层与层之间的神经元实现权连接，而每一层神经元之间不连接。其主要思想是把学习过程分为正向传播和反向传播两个阶段。在正向传播阶段，给定输入信号，通过输入层传播到隐含层并经过网络的权重、偏置值和神经元的转移函数作用后，从输出层做出响应。如果响应值和期望值的差值大于规定值，则转入误差反向传播阶段。这时，由于在输出层没有得到期望值，所以逐层递归计算实际响应与期望值之间的差值(即误差)，然后将误差通过隐含层向输入层逐层返回并将按“递归下降”的原则“分摊”给各个神经元，从而获得各层神经元的误差信号，以此作为修改权重的依据。在这两个过程的反复作用下，网络对输出模式相应的正确率也不断上升，最后网络在允许的误差范围内达到平衡状态而自动收敛［2，4-5］。

图1 典型BP网络3层结构示意图

2 BP网络设计

2.1 输入层和输出层

这里的输入层和输出层主要是基于用户确定的神经元数目。采用历史的沉降值作为预测将来沉降值的基础，涉及到怎么选择合适的历史数据，经过大量反复试算比较，选用3输入和1输出层结构(表1)，并且将数据滚动式地输入程序。这样设计，在预测精度、预测工作量、计算机耗时等方面都是合适的［4］。

表1 网络的输入输出模式

2.2 隐含层及隐含层神经元数目的确定

具有偏差和至少一个S型隐含层加上一个线性输出层的网络，能够逼近任何有理函数这个理论已经得到证明［6-8］。其设计BP网络的基本原则是:优先考虑增加隐含层中的神经元个数而不是增加隐含层的层数。因为，尽管增加层数可以进一步降低误差，并提高精度，但是这样同时会增加网络的复杂程度，相应也增加了网络的训练时间。而实际上，误差精度的提高也可以通过增加隐含层中神经元的数目获得，同时，其训练效果也比增加层数更容易观察和调整。通过上面的分析，本文隐含层数目取为1层。

对于隐含层，若神经元数量过少，则网络容错性差，识别未经学习的样本能力差;若神经元个数过多，网络的训练时间会明显增加，并且，随着样本中非规律性内容(如干扰、噪声)的存储，导致泛化能力降低。本文采用经验公式，并加以多次试算，最终取神经元个数为9。

3 工程实例

本文所采用数据为作者在苏州地铁2号线某工程实习期间监测收集所得。苏州地铁2号线某工程建设场地为广阔的太湖冲积平原，水系发达，地势平坦，系典型的水网化平原。工程所在场区在标高-48.57m以浅范围内揭露的地基土除表层为全新人工堆积物外，其下均为第四系晚期覆盖的冲积湖相、海陆交互相沉积物，岩性主要为黏土、粉质黏土、粉土、粉(细)砂等。工程始于2010年4月22日，并于2012年9月结束。实际中，选取该工程1号出入口1CJ2-2测点作为监测对象并进行短期预测，部分监测数据及结果见表2。

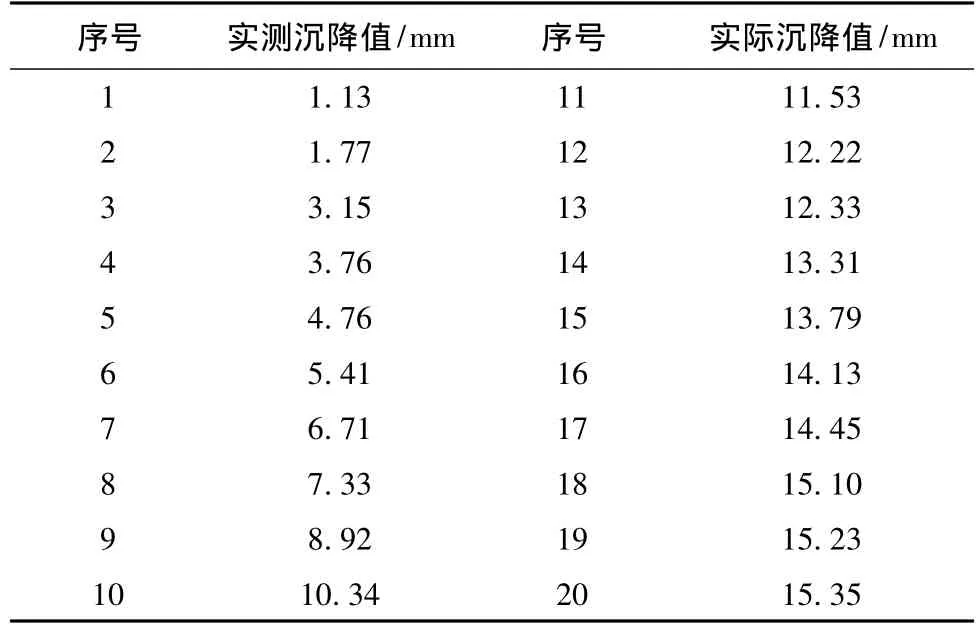
表2 监测数据

将表2的内容按照表1的滚动式方法写入Matlab，前14组数据作为训练样本，15～17组数据作为检验样本，以下是基于 Matlab7.0的BP预测网络的主程序:

clear;

clc;

p1=［1.13 1.77 3.15］;

p2=［1.77 3.15 3.76］;

…

p14=［13.31 13.79 14.13］;

p15=［13.79 14.13 14.45］;

p16=［14.13 14.45 15.10］;

p17=［14.45 15.10 15.23］;

p18=［15.10 15.23 15.35］;

P=［p1’p2’… p13’p14’］;

T=［3.76 4.76 … 14.13 14.45］;

［pn，minp，maxp，tn，mint，maxt］=premnmx(P，T)

net=newff(minmax(pn)，［3，9，1］，{'tansig'，'logsig'，'purelin'}，'trainlm');

Net=init(net)

net.trainparam.show=10;

net.trainparam.epochs=1000;

net.trainparam.goal=1e-6;

［net，tr］=train(net，pn，tn);

y1n=sim(net，pn);

y1=postmnmx(y1n，mint，maxt);

a=［p15'p16'p17'］;

pnewn2=tramnmx(a，minp，maxp);

anewn2=sim(net，pnewn2);

y2=postmnmx(anewn2，mint，maxt)

网络训练曲线如图2所示。

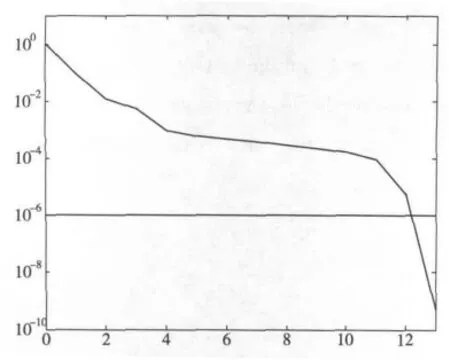
图2 网络训练曲线

由图2可见，此模型的短期预测仅进行了13次训练便结束，最终结果 y2=14.5567、14.6868、14.9631。由上述程序可知y2预测的为序号18～20的值。与实测值比较结果见表3。

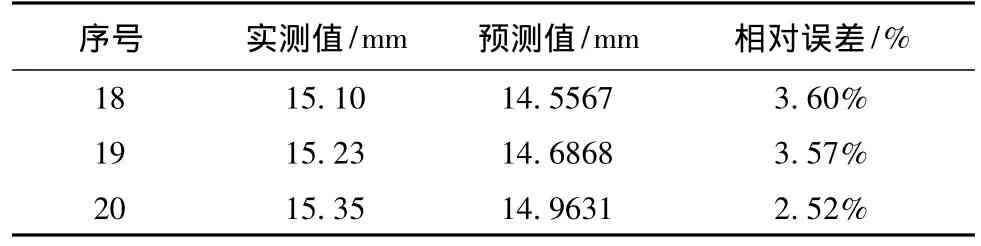
表3 模型精度

3 误差检验

这里采用平均绝对百分误差［10］(MAPE)来衡量预测精度。平均绝对百分误差为100，其精度分级原则见表4。

经计算，此例中MAPE=3.23，可见，上述方法属于高精度预测，适合基坑周边沉降的短期预测。

表4 预测精度划分表

3 结论

(1)BP神经网络较其他模型，更适合于处理高度非线性数据的拟合和预测。文中提供的沉降监测值仅20组，但是该方法同样适合于处理大数据量的情况。

(2)通过将监测数据滚动式的输入，可以预测下一步基坑周边地表的沉降值，可为沉降的控制和采取相应措施提供参考，同时对最终沉降量的预测结果也有一定的工程参考价值。

致谢:感谢同济大学许恺副教授和博士生汪江师兄给予学习和生活上的帮助，感谢上海同济建设工程质量检测站苏州轨道交通2号线现场监测项目组成员卢元庆、赵静、卢尚强、赵磊及中铁二局股份有限公司苏州轨道交通2号线Ⅱ-TS-04标项目经理部的帮助。

[1] 张乐.地铁隧道施工地表沉降预测模型及实证研究[D].武汉:华中科技大学,2011.

[2] 彭 涛,杨岸英,梁 杏.BP神经网络-灰色系统联合模型预测软基沉降量[J].岩土力学,2005,26(11):1810-1814.

[3] 齐干.基于BP网络的深基坑变形预测研究[D].桂林:桂林工学院,2004.

[4] 王玉雯.昆明深基坑变形监测与预测的应用研究[D].昆明:昆明理工大学,2011.

[5] 余江,陶宇.BP神经网络和灰色系统预测模型在深基坑地表沉降中的应用[J].浙江水利科技,2010(3):80-82.

[6] 张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2009.

[7] Robert Hechi-Nielsen.Theory of the back propagation neural network[C]//Harry Wechsler.Proceedings of International Joint Conference on Neural Networks,Orlando,Florida,USA,February1-5,1992:65-93.

[8] 罗 毅,姚 毅,李 莺,等.基于BP神经网络的输电线路覆冰增长模型研究[J].四川理工学院学报:自然科学版,2012,25(1):63-66.

[9] 傅荟璇,赵 红.MATLAB神经网络应用设计[M].北京:机械工业出版社,2010.

[10] 贾萍,方源敏,卢水牯.Logistic模型在高层建筑沉降监测中的应用[J].河南科学,2011,29(3):329-332.