高精度图像尺寸检测镜头畸变校正方法与实现

黄 湛，徐 杜，蒋永平

(广东工业大学 信息工程学院，广东 广州510006)

随着现代工业企业的发展要求，计算机视觉在非接触测量检测［1］这一领域占据了越来越主要的地位。现代工业的高精度要求对于计算机视觉，既是机遇又是挑战。在进行高精度检测时，图像不但对噪声的影响敏感，相机镜头采集图片时产生的几何畸变，更是导致检测精度下降的元凶，细微的畸变，也会造成精度严重滑坡。只有真实的图像，才能真实地反映物体的真实形态。如何更好地适应现代工业化发展要求，高精度图像检测镜头畸变校正具重要意义。

镜头畸变的产生原因取决于相机镜头的生产工艺和安装工艺，对于一般定焦相机往往可认为是由若干个畸变常数所得到的，故理论上可以认为只需一次标定即可解决。实际上，标定效果既受图像处理和标定数学模型［2］所影响，亦受到成像质量的好坏所左右，标定图像若与之后的图像质量偏差较大时，会造成图像处理效果出现偏差，导致标定效果大打折扣，实际的标定并非一次到位，需要间隔一段时间重新进行标定。故研制方便快捷的标定系统是目前相机标定的一个发展趋势。目前国内外具有代表性的相机标定方法包括了Faig［3］提出的对于相机内外部参数标定的非线性优化算法、Tsai［4］给出的基于径向约束的两步标定法(RAC)，以及张正友的基于平面格网标定法和张永军的基于平面格网［5］和二维直接线性变换方法等。这些优秀的标定方法给工程应用提供了有力的理论依据，但在实用性和精度上仍有必要进一步深入研究，其发展趋势大致如下:(1)从畸变模型方面考虑，研究适用于高精度测量的标定方法。(2)结合特定的标定对象，研制实用型标定系统。(3)从通用性出发，研究灵活稳健的自标定算法。在线阵相机标定中，鉴于主体畸变为径向畸变，以Tsai的RAC［6］两步法算法应用最为广泛。在建立世界坐标到图像坐标的转换模型基础上，对图像坐标引入畸变参数，建立畸变数学模型，再通过Levenberg－Marqyardt(LM)或Newton Raphson(NR)算法对初始结果进行深度优化以得到精确值，平均精度可达1/4 000，深度方向精度可达1/8 000。本文通过改进RAC算法，结合检测对象，设计了适用于测量设备的标准件，研究了实用型标定方法。

1 线阵CCD几何成像原理

摄像机的三维世界坐标转换到图像坐标的几何模型如图1所示。设被测物体所在的世界世界坐标系为OwXwYwZw，Yw为被测物体的运动方向，相机坐标系为OuXuYuZu，图像坐标系为OXY，Y为被测物体的运动方向。3个坐标系的各坐标轴分别平行。由图像坐标系与世界坐标系的线性关系，可实现世界坐标到图像坐标的转换。

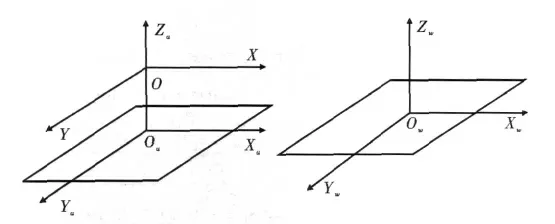
图1 图像坐标几何模型

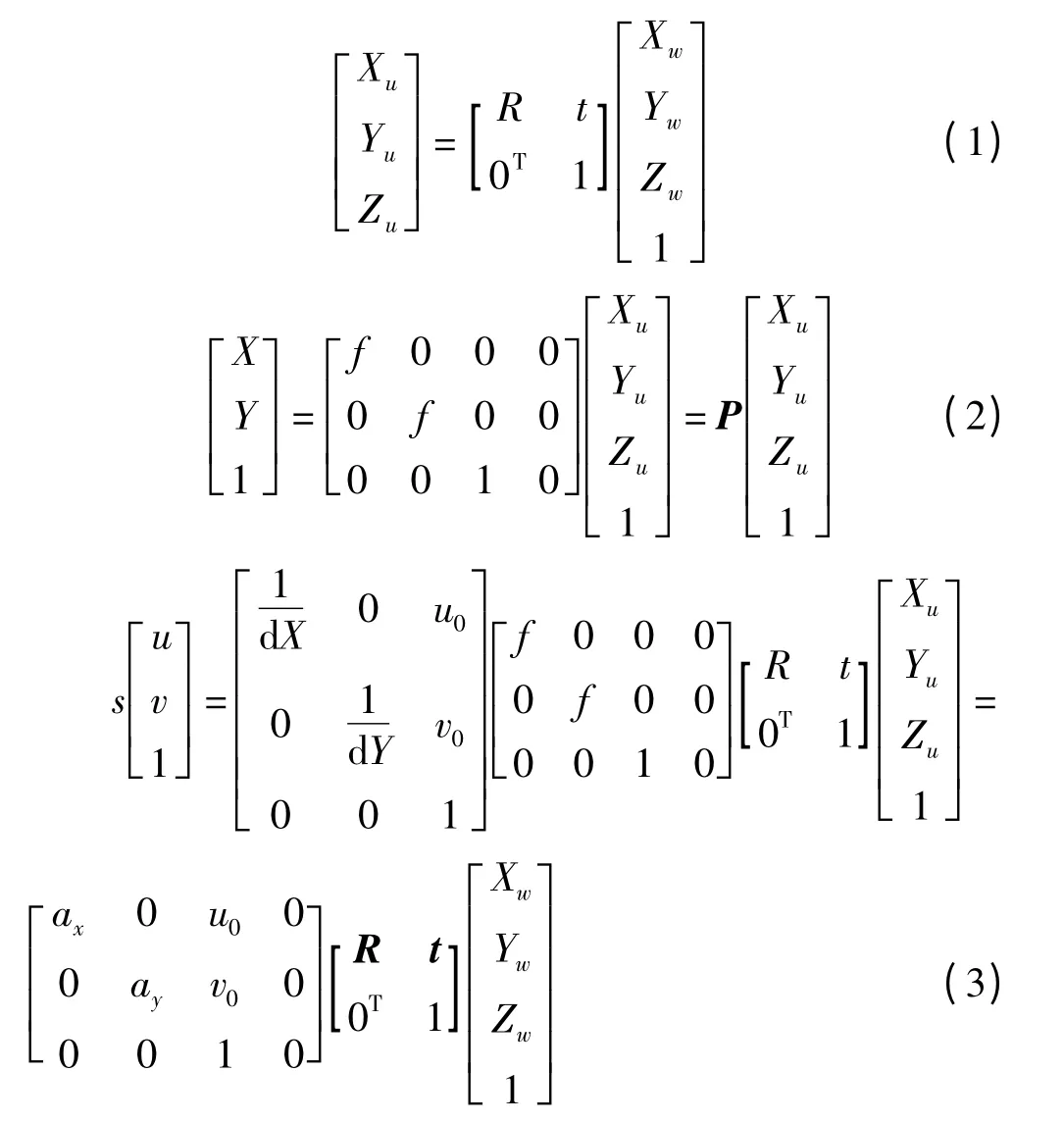
其中，s为比例因子，ax，ay分别为u轴，v轴上归一化焦距。R、t分别为世界坐标系转换到相机坐标的旋转矩阵和平移矩阵。在系统中，测量物在Z轴方向固定，采集图为一维图像，故可将Y、Z轴单位化，由式(1)和式(2)可得

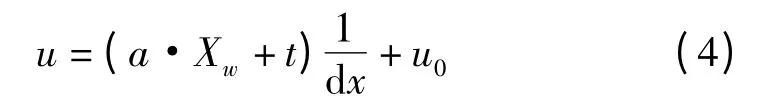
实际上，实际镜头并不是理想的透视成像模型，这使得物体在成像过程中并不位于线性模型中所描述的位置X，而是畸变后的实际像平面坐标X'。故有

其中，δx为畸变值，其大小与图像点坐标在图像中的位置相关。

切向畸变［7］对线阵CCD影响很小，一般忽略不计，故只考虑径向畸变。径向畸变的修正量可由以下多项式模型表示

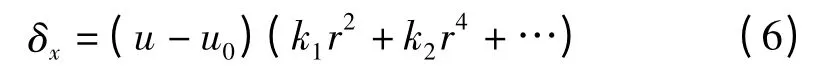
其中，r为图像上所求点到光心的距离。至此，由式(4)和式(6)可得物体从世界坐标转化到图像实际图像坐标的映射关系。

2 标准件设计

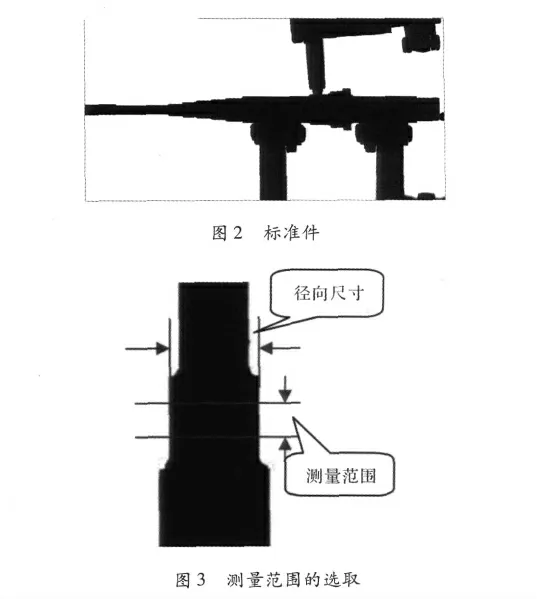
标准件如图2所示，各阶梯按从小到大分布，最大不超过CCD相机的最大视野。如图3所示，取各阶梯中间部分为测量范围，测量的径向尺寸为该阶梯的径向尺寸，从而避免各阶梯间接合处加工不好而导致该范围内径向尺寸测量结果不稳定。

3 畸变校正过程实现

传统的畸变校正是利用标定板对图像进行全图标定，当图像过大时，会造成标定时间过长而影响图像检测的实时性，无法满足工业上图像检测的实时性要求。为保证畸变校正的精确度和效率，本系统对畸变校正模型进行优化。由于该系统检测目标为径向尺寸，设标准件各阶梯径向尺寸为li，则li=Xi1－Xi2，联合式(4)和式(6)得

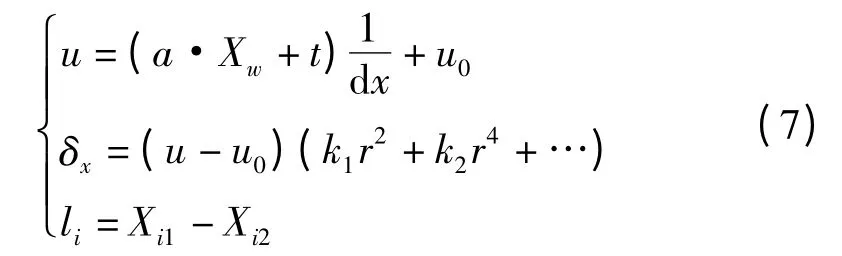
由该方程组可将平移向量t消去，令dx/a=a，故有

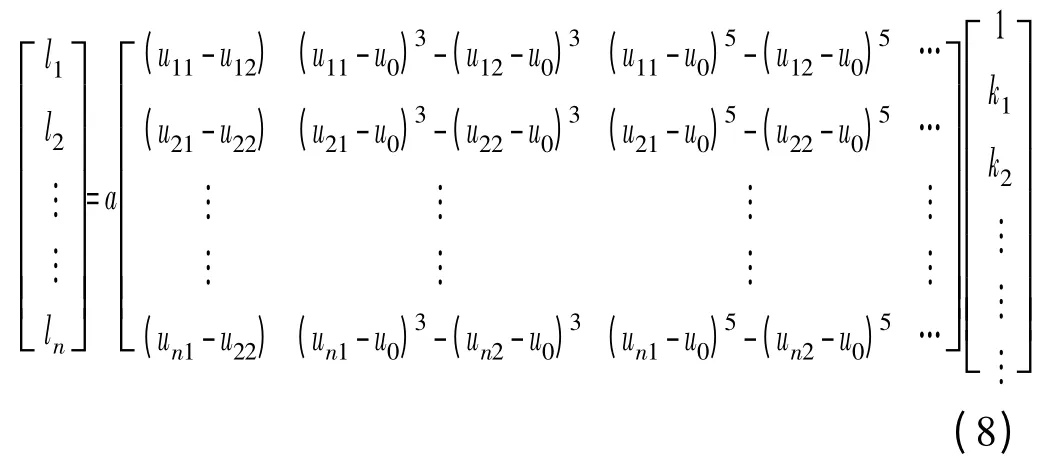
取初始值u0为图像的中心坐标，k1、k2、k3、…等均为零，利用Sobel算子提取出各阶梯上下两端的亚像素边缘坐标，再将各阶梯的径向尺寸li代入则可求得a的初始值，将求得的a、u0代入式(8)，用Levenberg－Marquardt(LM)深度优化算法进行优化搜索［8］，得到a、u0、k1、k2、k3、…的精确解。该方法可消去坐标转换中的平移参数矩阵［9］，降低了算法复杂度，提高了标定［10］过程的运算速度。

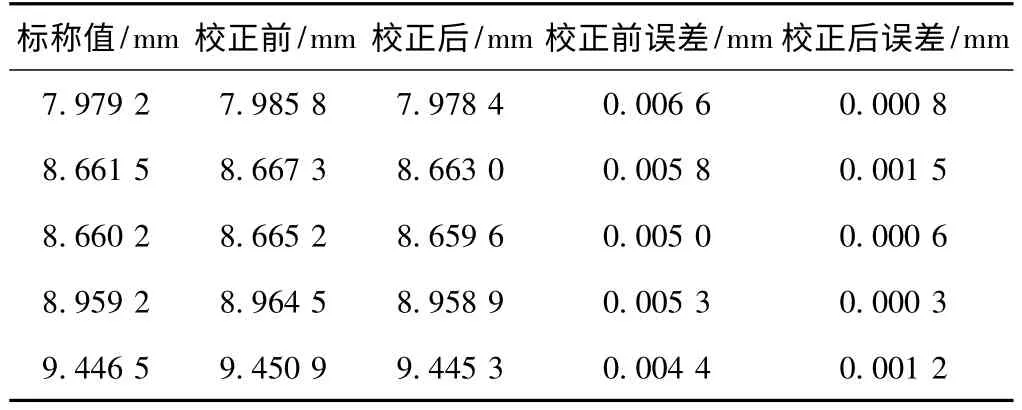
表1 标准件畸变校正后测量数据与真实数据对比

4 实验结果与分析

本文所讨论的镜头径向畸变算法［11］已经在汽车发动机气门检测系统得到应用，系统所使用的线阵CCD采用的是分辨率为8 192×1的线阵相机［12］，标准件如图4所示，通过微距位移［13］平台，令标准件进行微步距移动，经扫描采集可得到如图2所示的实物图。用VS2008将算法进行编程实现，通过10组阶梯的边缘坐标对方程组(7)进行求解，可得a、u0、k1、k2、k3、…的精确解。表1为通过畸变校正后的测量数据与真实数据的对比。由表1数据可得，标准件经过畸变校正后的测量数据与给定的标准数据偏差在0.014～1.3μm之间，满足工业上测量的高精度测量标准。

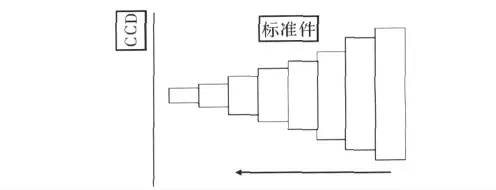
图4 线阵相机标准件

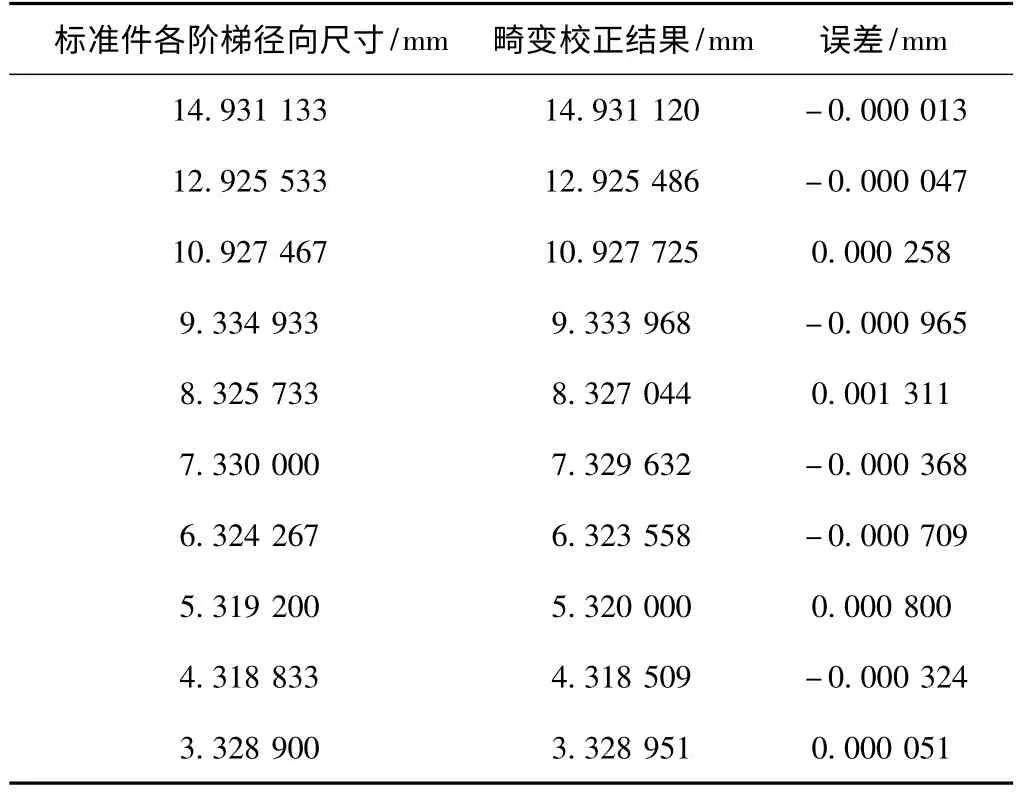
表2 抽样品畸变校正后测量数据与真实数据对比

为验证畸变校正算法的可行性，任意抽检了数种气门进行测量，表2为畸变校正前后及标称值的数据。通过数据分析可知，畸变校正前的测量误差为4.5μm以上，通过畸变校正，可以使测量精度提高到2μm内，通过径向畸变校正提高测量精度是可行的。

5 结束语

线阵CCD在工业高精度测量中有着较大的优势，其高分辨率可以更细致地还原被测物的真实边缘，有效提高测量精度。在本检测系统的研发中，除采用高分辨率和高精度的线阵CCD工业数字相机和高档相机镜头外，还开展了如下工作:

(1)设计了镜头畸变校正用的阶梯状标准件，该标准件加工精度高，保证了标定物的高精度要求，为接下来的畸变校正工作提供了稳定且可靠的标定物。同时，该标准件大幅提高了标定物对各类相机的适应性，为镜头畸变校正应用于线阵CCD的理论依据提供了强有力的物质依托。通过线阵相机高分辨率的优势和镜头畸变校正方法的有机结合，实现了高精度图像尺寸检测。

(2)本系统对Tsai的RAC标定法进行改进，由传统的点对点畸变校正转换为尺寸/尺寸的畸变校正，从而建立误差补偿曲线的高次拟合函数，实现镜头畸变校正［14］。该方法简化了畸变参数个数，降低了算法的复杂度，从而提高了镜头畸变校正的效率，满足实际检测过程的实时性要求。通过使用该方法，系统检测精度可提高至2μm，满足实际测量中的高精度图像尺寸检测要求。

目前，该系统现已应用于企业气门检测线中，为提高检测精度、提高产品质量、减少售后赔偿、发挥了积极作用。

［1］ 牛建军，刘上乾，姚荣辉，等.高准确度光电成像测量系统图像畸变校正算法［J］.光子学报，2006(9):1317－1320.

［2］ 陈宝林.最优化理论与算法［M］.北京:清华大学出版社，2005.

［3］FAIG W.Calibration of close－range photogram－metric systems:mathematical formulation.Pho－togrammetric eng［J］.Remote Sensing，1975，41(2):1479－1486.

［4］TSAI，ROGER Y.An efficnent and accurate camera calibration technique for 3D machine vision［C］.Proceedings of IEEE CV PR'，1986:364－374.

［5］ 范勇，张佳成，陈念年，等.图像几何畸变校正方法［J］.计算机工程与应用，2009，45(29).194－197.

［6］ 张广军.视觉测量［M］.北京:科学出版社，2008.

［7］ 张洪涛，段发阶.基于两步法线阵CCD标定技术研究［J］.计量学报，2007，28(4).311－313

［8］ 姜大志，郁倩.计算机视觉成象的非线性畸变研究与综述［J］.计算机工程，2001，27(12):108－110.

［9］ 郑南宁.计算机视觉与模式识别［M］.北京:国防工业出版社，1998.

［10］骆文博.王广志，丁海曙，等.基于线阵CCD的高精度位置检测［J］.清华大学学报:自然科学版，2002，42(9):1139－1143.

［11］林慧英，苏建，刘玉梅，等.基于图像畸变矫正的摄像机标定方法［J］.吉林大学学报:工学版，2007，37(2):433－437.

［12］马登极，朱善安，王长军.线阵CCD在高精度测径系统中的应用［J］.计算机测量与控制，2006，14(2):175－176.

［13］解凯，郭恒业，张田文.一种具有径向畸变校正的图像整合算法［J］.电子学报，2004，32(10):1726－1729.

［14］李会军，宋爱国.增强现实中的摄像机径向畸变校正［J］.传感技术学报，2007，20(2):462－465.