宽带延时宏模型高效延时提取方法

刘飞飞，张松松

(西安电子科技大学 电路CAD研究所，陕西 西安710071)

随着电路工作频率的升高及信号上升沿的减小，信号完整性(Signal Integrity，SI)，电源完整性(Power Integrity，PI)问题越来越突出。现代高速电路设计已不能单凭经验来完成，必须借助EDA工具建模仿真实现。目前全波仿真工具虽然仿真精度高，但耗时大且不适于系统整体仿真。宽带宏模型技术的出现为无源互连建模提供了一种高效精确的建模方法，并可获得Spice兼容模型方便系统级仿真。延时宏模型(Delay－based Macromodel)是在宏模型基础上发展而来的，主要针对电大尺寸互连建模，可以良好地建模电大尺寸互连延时特性，获得低阶宏模型以提高仿真效率。

延时提取(Delay Estimation)是延时宏模型建模的首要步骤，延时估计的精度直接影响延时宏模型建模的精度及模型复杂度。目前延时提取方法主要包括:时域中Hilbert变换法［1－2］和Wavelet变换法［3］、频域中Gabor变换法［4－5］。Hilbert变换法利用最小相位系统概念，忽略了高阶反射项，仅提取单个主要延时项。而实际中延时宏模型包含多个延时项，因此这种方法提取延时对于延时宏模型建模是不充分的。Wavlet变换法及Gabor变换法，采用时－频域分解思想，可以实现多个延时项的提取，但是二维变换算法的性质决定其较为耗时。

针对目前延时提取中存在的缺陷，本文提出一种基于傅里叶反变换(Inverse Fourier Transform，IFT)的方法，主要用于从频域离散数据中提取多个延时项。经验证本方法较好地实现多个延时项提取并大幅提高了计算效率。

1 方法基本原理

1.1 基于Gabor变换的延时提取方法

Gabor变换法提取延时由S.Grivet－Talocia于2006年提出［4］，主要针对电大尺寸互连频域离散数据延时宏模型建模中的延时项估算。Gabor变换是一种时－频域分解，其算法实现流程［5］如下:

(1)对互连频域离散数据H(jω)进行频域Gabor变换，获得时－频域分解二维数据

其中基函数为

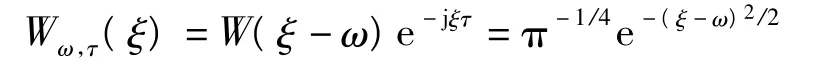
基函数已经经过归一化。其中τ在物理意义上代表着系统时间或延时。实际计算中积分上下限按照频域数据有效带宽Ω计算。

(2)对式(1)所得结果沿频域有效带宽取平均值，从而将二维的时－频域结果转化为一维时域结果

上式中所得结果具有时域瞬态功率特性，但又不完全是时域瞬态功率。

(3)对式(2)所得具有时域瞬时功率特性结果进行局部峰值能量量化，即沿每个局部峰值两边的局部谷值构成的时域区间进行积分，这样积分所得结果具有能量物理意义

其中，m表示第m个局部峰值。

(4)对于式(3)获得的m个峰值及其量化能量，按照其能量大小，设定阈值δ，进行主要延时项筛选

通常阈值δ较小，被忽略的延时项能量贡献小，不会对最终延时宏模型精度造成明显影响，然而延时项减少后，所得宏模型仿真效率将得到较大提升。

基于Gabor变换的频域延时提取方法中主要结果如图1所示。

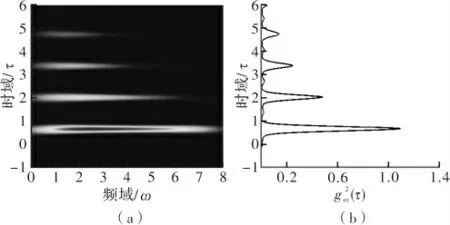
图1 Gabor变换法提取延时流程主要结果图

图1(a)代表时－频域坐标下的Gabor变换后所得数据，其具有能量密度的意义。图中颜色越亮代表能量密度越高。图1(b)中曲线具有类似时域瞬态功率的意义，其局部峰值处表征此时刻能量比较集中。可以看出:图1(a)与图1(b)能量密集的时刻点是相对应的，这就是系统延时项对应时刻。

1.2 基于IFT的延时提取方法

由于Gabor变换法中采用了二维时－频域分解，这正是其算法耗时的根源所在。通过对其算法流程研究，其时－频域分解中获得大量冗余信息，而真正用于延时提取的是沿频域带宽取均值后所得类似瞬时功率的时域数据。由此启发可以绕过二维时－频域分解，通过IFT法，直接获得其时域瞬时功率用以提取主要延时项。本文提出的基于IFT的频域延时提取方法流程具体如下:

(1)对原始频域离散数据作傅里叶反变换，因实际中频域数据具有一定带宽限制，即在其全频带响应上添加一个门函数

其中，Ω为频域数据带宽;GΩ(ω－ω0)表示中心频率位于ω0;门宽度为Ω的频域门函数;H(jω)为理想全频带响应，其与GΩ(ω－ω0)乘积便是实际中频域离散数据。由IFT性质可得

式中，h(t)为全频带响应H(jω)的傅里叶反变换，中括号内的Sinc函数GΩ(ω－ω0)为门函数的傅里叶反变换。对于电大尺寸无损互连来说，其全频带时域响应在延时项处对应一个脉冲波形，如图2(a)所示。实际中的互连在其延时项处对应的不再是一个脉冲，而是退化为很窄的尖峰。式(5)中门函数的出现，即频域带宽特性，将在时域中引入Sinc函数，从而把延时项处尖峰值进一步展宽，如图2(b)所示。并且在各延时项之间由Sinc函数旁瓣叠加产生许多噪声峰值，对延时项处峰值的识别造成干扰。因此必须进行适当的后处理，从众多噪声干扰峰值中提取主要延时项。同时可以观察到图2(b)中延时项处的峰值能量比非延时项处能量大，这正是本文提出方法可以有效提取延时项的原因。

(2)提取时域瞬时功率的局部峰值，采取与Gabor变换法类似的峰值能量量化措施，如下式

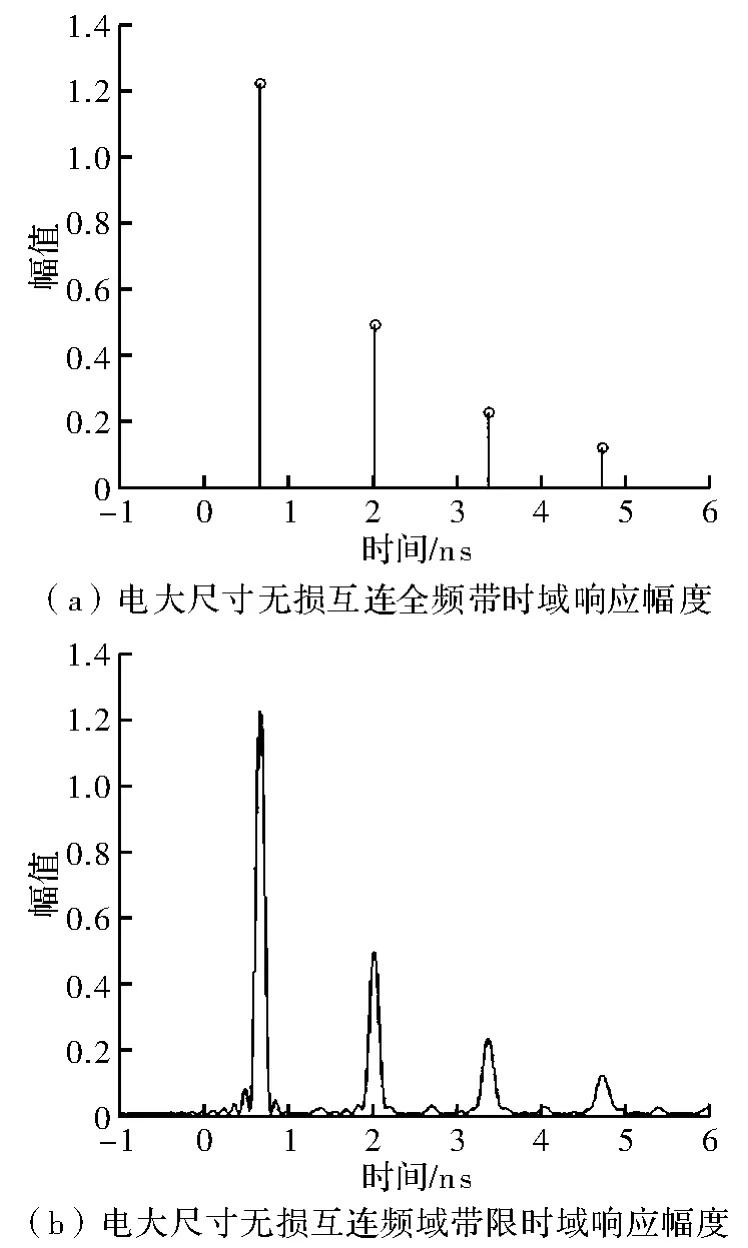
图2 电大尺寸互连时域响应

(3)对量化后能量包络曲线进行峰值提取以获得对应延时项

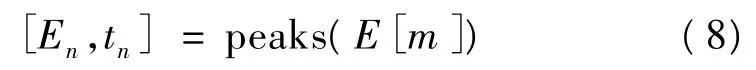
其中，En与tn分别表示二次峰值提取得到的第n个局部峰值对应能量量化值与时刻点。

(4)设定阈值选取主要延时项

其中，δ为设定阈值，通常此阈值范围比较小，可以依照建模精度来选择，一般选择范围0.01～0.05。

在本方法流程中，注意到因频域带限效应在时域中引入Sinc函数使延时项处尖峰展宽，而频域带宽越窄其时域展宽特性越明显，甚至会出现主瓣叠加效应从而严重干扰延时项提取。因此为提高算法精度及鲁棒性，本文进一步研究了该算法的适用条件，在此给出一个粗略的充分条件

其中，Ω表示频域数据带宽;τ表示互连基本延时。τ可通过下式进行估算

其中，l表示互连等效物理长度;c为真空中光速;εr为互连线中介质相对介电常数。在满足条件式(10)的情况下，可以保证频域带限特性在时域中引入的Sinc函数第一旁瓣不重叠，如图3所示，这样可以保证主要延时项的估算精度。

图3 基于傅里叶反变换的延时提取方法适用条件

图3所示频域带限特性在时域延时项处引入Sinc函数效果，如图中虚线与点线分别为延时项与处的Sinc函数。保持其第一旁瓣不重叠时获得的叠加后瞬时功率曲线为实线，其在延时项处对应一个较大峰值。虽然因叠加效果造成处峰值偏移，但因其能量贡献较小，仍然可以保证所提取延时项的精度足以满足延时宏模型建模要求。

2 实验验证

根据提出的延时提取方法，选取一个不连续长传输线的例子来验证其延时提取效果，并与基于Gabor变换的延时提取方法进行对比。通过HFSS建模仿真图4所示不连续长传输线模型，获得0.05～10 GHz范围内的频域响应Y参数离散数据。其中传输线长120 mm，线宽1 mm，在其中心60 mm处有一过孔，PCB参考平面尺寸为50 mm×120 mm。

图4 不连续长传输线模型

将HFSS仿真所得Y参数离散数据分别进行Gabor变换与傅里叶反换提取延时。由于本模型满足对称互易特性，即Y21=Y12，Y11=Y22，故只对其中的Y11，Y21参数进行延时提取即可获得整个二端口网络延时结果。两种延时提取方法对比结果如图5和图6所示。

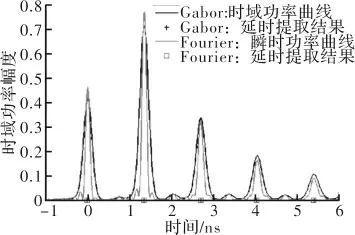
图5 Y11延时提取结果对比图

图6 Y21延时提取结果对比图

如图5和图6所示，基于Gabor变换的延时提取方法获得的时域功率曲线(黑线)与本文提出方法获得的时域瞬时功率曲线具有高度一致性，并在相应延时项处都存在较大尖峰值。同时观察到本文所提方法在延时项附近有较多旁瓣干扰峰值的存在。图5和图6所示两种方法所提取延时结果几乎完全重合。具体提取延时项值及两种方法在计算速度上的对比如表1所示。

表1 两种延时提取方法结果对比

如表1所示，文中提出的方法与基于Gabor变换的延时提取方法相比，所提取延时项结果一致。但在计算速度方面，本文方法具有明显优势，约为Gabor变换法速度的580倍。由于Gabor变换属于时－频域二维分解，每一个时间点对应一次加窗傅里叶反变换。因此理论上利用Gabor变换提取延时的算法复杂度是本文方法的N倍(N为时域数据点数)。Gabor变换法的计算复杂度与精度之间存在矛盾，实际中必须以算法速度来换取延时提取的精度，这是Gabor变换法的另一弊端所在。而本文提出的方法不存在这种矛盾，采用傅里叶反变换，同时计算获得所有时间点信息，计算复杂度主要取决于频域数据点数。

3 结束语

文中提出了一种针对频域离散数据的高效延时提取方法，并进行了实验验证。本方法基于傅里叶反变换(IFT)，与基于时－频域分解的方法不同，其计算复杂度几乎不受时域点数影响，主要取决于频域响应数据点数。而其延时提取精度主要取决于频域数据带宽及时域采样间隔与点数。本文在计算精度与速度上与基于Gabor变换的延时提取方法作了对比，对比结果表明本方法在提取延时效率方面的优势明显，适合频域延时宏模型建模中延时项的提取，会在较大程度上提高延时宏模型建模的整体效率，具有一定的实用价值。

［1］MANDREKAR R，SWAMINATHAN M.Causality enforcement in transient simulation of passive networks through delay extraction'［C］.9th IEEE Workshop Signal Propagate，2005:25－28.

［2］MANDREKAR R，SWAMINATHAN M.Delay extraction from frequency domain data for causal macro－modelling of passive networks［C］.IEEE International Symposium on Circuits and Systems，2005:5758－5761.

［3］CHAREST A，NAKHLA M S，ACHAR R，et al.Time domain delay extraction－based macromodeling algorithm for longdelay networks［C］.IEEE Transactions on Advanced Packaging，2010:219－235.

［4］GRIVET TALOCIA S.Delay based macromodels for long interconnects via time－frequency decompositions［C］.IEEE Topical Meeting Electrical Performance Electronic Package，Scottsdale，2006:199－202.

［5］CHINEA A，TRIVERIO P，GRIVET－TALOCIA S.Delaybased macromodeling of long interconnects from frequencydomain terminal responses［J］.IEEE Transactions on Advanced Packaging，2010，13(1):246－256.