欠采样相关时差算法分析及多普勒误差校正
崔昕昕
(西安电子科技大学 电子工程学院,陕西 西安710071)
时差法(Time Differences of Arrival,TDOA)是当前高精度无源定位的主要方法之一。在众多领域内具有广泛应用,例如雷达、声纳、地理以及生物医学等。基本的时差估计方法包括广义相关法、广义双谱估计法、全波形比较法及自适应估计法等[1]。
在时差估计算法中,相关时差估计算法[2]是最经典的算法之一。其通过求得站间接收信号的自相关函数与互相关函数最大峰值出现的时间差来估计站间时差。
雷达侦察机前端的信号频率通常效高,对数字采样提出了高要求,在这种情况下,欠采样方法[3]就显得尤为重要。如何将高频信号通过合理的采样频率恢复出来,是一个实际问题。
本文的重点是通过多周期取点采样法,在欠采样的条件下对相关时差算法和时差估计时多普勒频移造成的误差进行分析,并做相应校正。
1 信号模型
TODA定位系统,如图1所示。由于各观测站在空间中位置不同,接收到的信号之间存在着时差,即站间时差。利用站间时差通过特定的算法可确定目标信源的位置。

图1 TDOA系统
假设目标信源是运动的,则信源和观测站的空间位置与速度可以分别表示为
其中,xT和vT分别是目标信源的坐标和速度;xOi是第i个观测站点的坐标。各观测站上信号的到达时间和彼此之间的时差可表示为
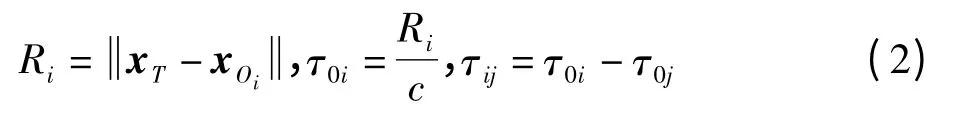
其中,Ri表示目标信源和第i个观测站之间的距离;τ0i表示信号到达第i个观测站的时间;τij表示第i个和第j个观测站之间的时延,即站间时差;c表示光速。
由于目标和观测站之间存在相对运动,观测站接收到的信号不仅存在时延,还存在着多普勒频率。假设目标辐射出的高频信号为s(t,f)是单载频脉冲信号,脉内调制的载波频率为f,脉宽为T,φ为脉冲初始相位。则信号可表示为
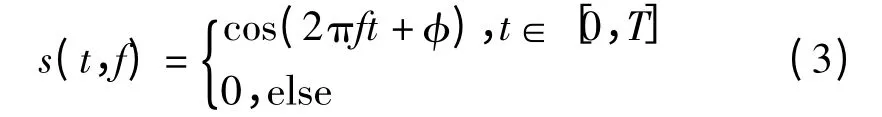
一般为计算方便,设φ=0。到达第i个观测站的信号可表示为s(t-τ0i,f-fdi),其中fdi为对应的多普勒频率,表示为
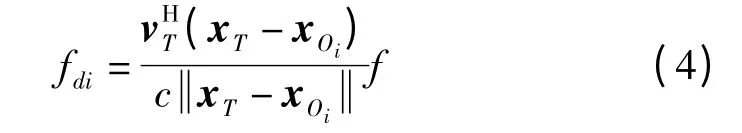
若观测站同样是运动的,则上式需改为
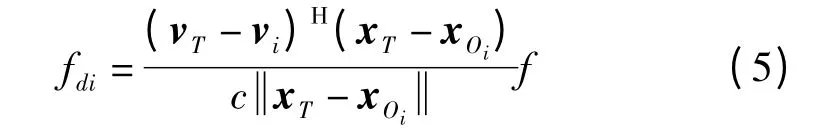
其中,vi是第i个观测站的运动速度矢量。当噪声存在时,第i个观测站上观察到的信号如下
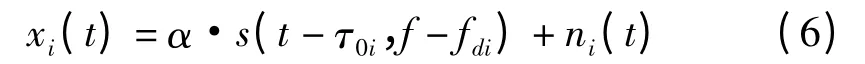
其中,ni(t)是第i个观测站上的噪声。
2 相关时差算法
常规雷达信号可表示为如下形式

如果不考虑初始相位φ和幅度a(t),上式可简化为s(t)=cos(2πfct),其中fc是载波频率。以采样频率fs进行采样后的数字信号可表示为s(k)=cos(2πkfc/fs)。
由奈奎斯特采样定理可知,当采样频率大于奈奎斯特采样频率,即fs≥2fc时,可以无失真地恢复出原信号,从而进行后续的处理,并可得到准确的时差估计。但在实际应用中,雷达信号的频率通常较高[4],即使在中频端也要数百MHz,且工程中的采样频率一般选择为奈奎斯特采样频率的3~5倍,即过采样。这对采样提出了更高的要求,因此有时较难实现。
在时差估计的应用中,采样频率的选择除了要考虑信号的恢复,还要考虑到避免估计结果的模糊性。解决这一问题的基本思路是:利用数字信号的特点,在欠采样的条件下,得到和过采样时相同的样点值,便能得到相同的时差估计结果。根据正弦信号的周期性,只要选择合适的采样频率,即可实现上述思想,同时也可灵活地调节采样频率。
在完成对信号的采样恢复后,便可通过各站上的接收信号求时域相关,得到站间时差[5],进而通过TDOA算法确定目标信源位置。
假设空间中存在两个观测站,由上节可知,观察到的信号如下
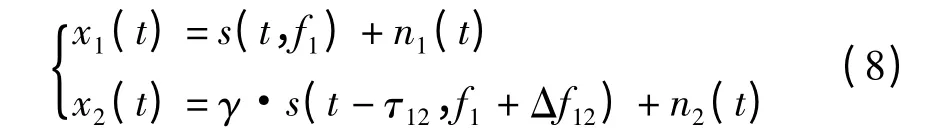
其中,为了计算方便,将观测站1上接收的信号时延看做时间零点,并将其增益视为1,其中,γ表示观测站2上的信号相对于观测站1的增益;Δf12=fd1-fd2表示观测站1和站2接收信号的载频差。
根据信号时域相关的定义,可得观测站1接收信号的自相关函数为
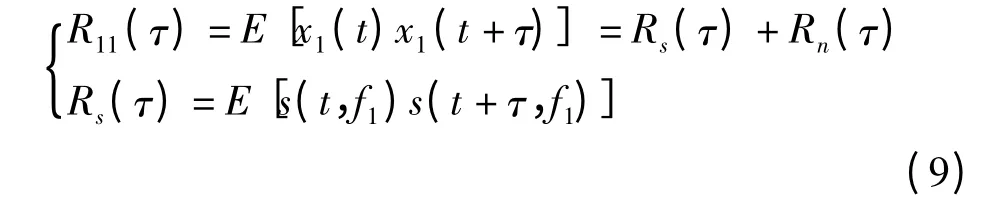
式中,将自相关分为信号部分Rs(τ)和噪声部分Rn(τ)。由于信号和噪声各不相关,因此显然有Rn(τ)=σ2·δ(τ)。同时,观测站1和2接收信号的互相关函数为
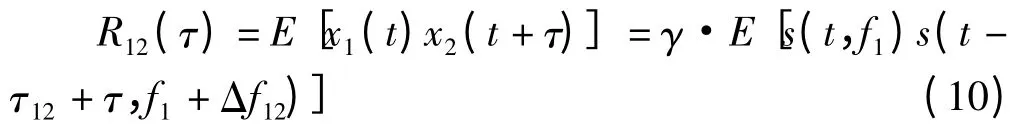
从以上两式中可观察出:当各站与目标的相对径向速度相等或均为0时,站间接收信号的载频是相同的,因此有观测站间接收信号互相关函数波形是由单站接收信号自相关函数波形平移所得,即
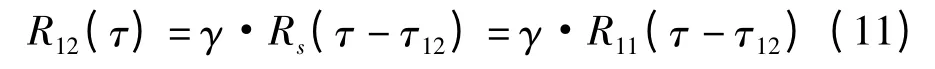
其中,平移量正好为站间时延τ12;放大系数为γ。因此只要找到两个函数波形各自的最大值,便可方便快速地求出精确的站间时差,如图2所示。
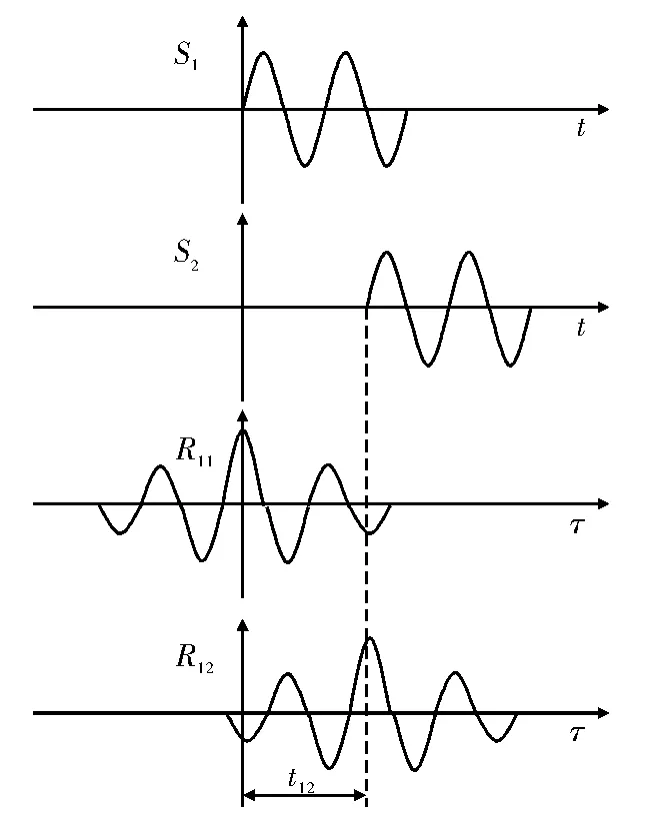
图2 相关法测时差原理
两个相关函数的峰值差就是两站接收信号的时差τ12[8-9]。
3 多普勒误差校正
然而当各站与目标的相对径向速度不相等时,由于站间接收信号的载频不再相同,R11(τ)和R12(τ)的函数波形也不再完全相同。此时再取两个函数波形的最大值,获得的是存在误差的站间时差估计值12[10]。
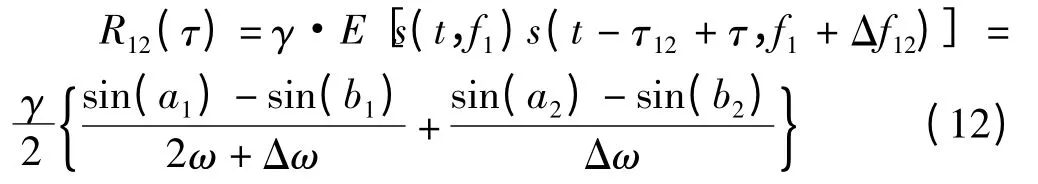
其中,ω=2πf1,表示观测站1上接收信号载频的角频率;同理,Δω=2πΔf12,表示站间多普勒角频率。a和b是实际的积分上下限,变换后的积分上限表示如下
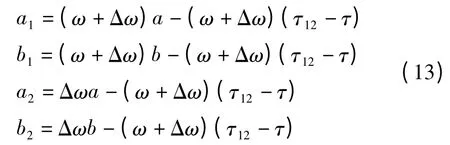
可以将积分域分成3种情况讨论,如图3所示。
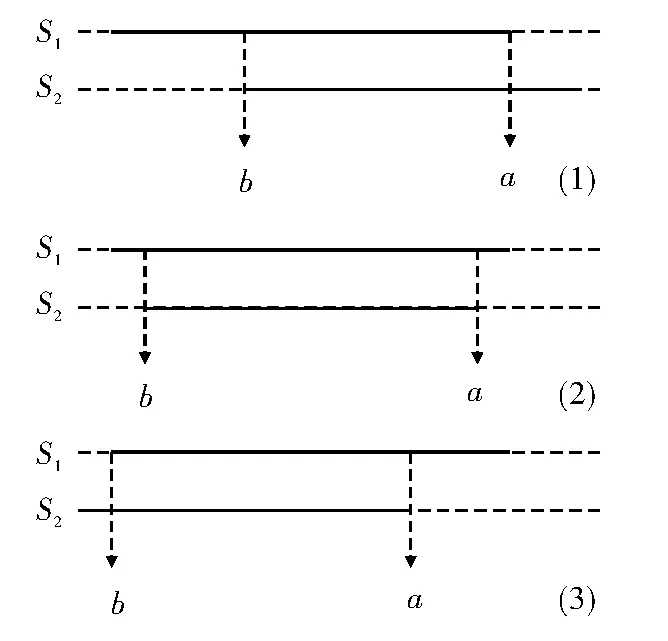
图3 两观测站脉冲区域关系
图3中,实线部分表示脉冲存在区域,虚线部分表示脉冲外区域,有效的积分区域应当是两观测站信号脉冲均存在的区域。
由于高频载波相关的特性,一般来说较宽的积分域对应较大的积分值。因此,认为互相关函数的最大峰值出现在第2段积分域内,在这种情况下式(12)可化简为
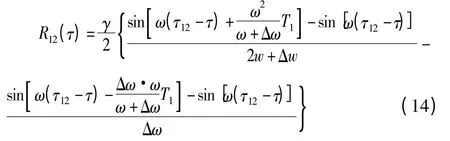
由于Δω≪ω,根据时域相关的特性,互相关的最大值在积分域最接近τ12的极值点取到。对互相关函数求一阶导可得
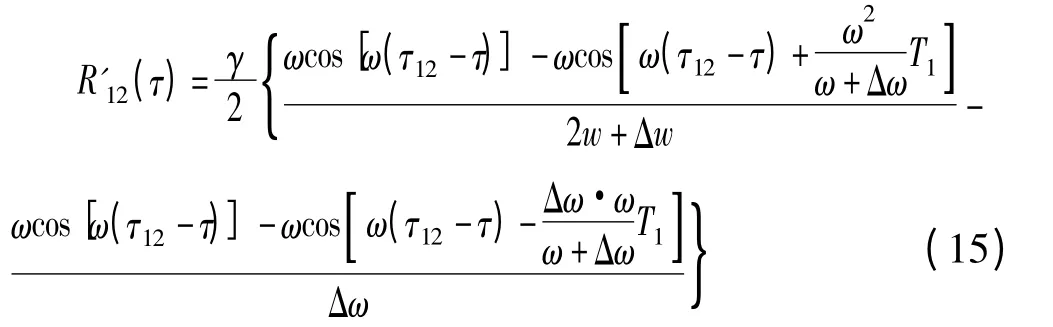
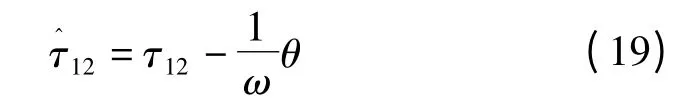
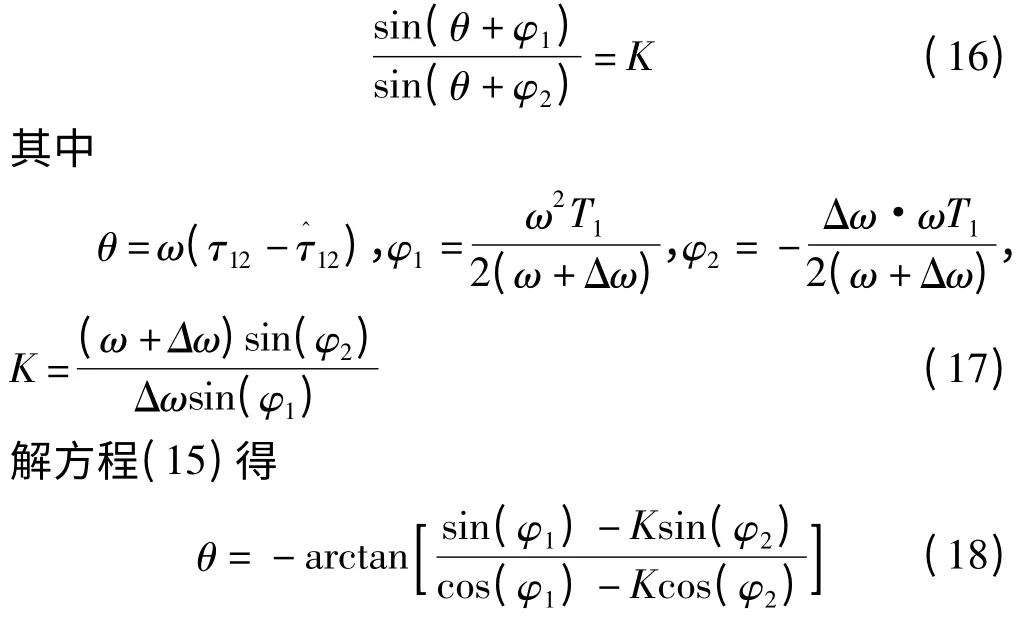
进而有时差估计的绝对误差约等于
通过以上分析可知,相关法估计时差误差与多普勒频率近似成正比。
综上所述,站间多普勒频率差会导致额外的估计误差。此种误差可通过频域相关处理来进行校正。
设观测站1和2接收到的信号的傅里叶变换分别为F1(ω)和F2(ω)。显然由于两观测站接收的是同一目标信源发射的信号,因此两个信号的频域波形相同,且只相差一个平移,平移量正好为站间多普勒频率差Δω,即
则接收站1和2上接收信号的频域互相关函数为
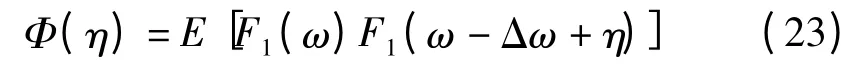
本文主要通过一维搜索法找到频域相关的最大值,进而得到多普勒频差的估计值Δ。得到频差估计值后,就可以对观测站2上的信号进行频差校正
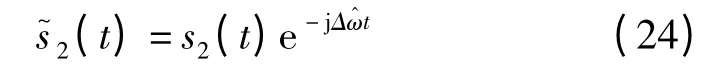
利用校正后的信号与接收站1上的接收信号进行互相关,可有效的减小由多普勒频率导致的站间时差估计误差。
4 仿真结果分析
以下给出了相关时差估计算法的计算机仿真,以及不同参数变量情况下的估计误差分析。
假设空间中存在着一个目标信源和两个观测站。目标信源发射高频脉冲信号,脉内载频为5 GHz,脉宽为1μs。观测站接收信号时的A/D采样率为400 MHz,在欠采样的条件下,通过多周期取点采样法完成对信号的恢复。实际站间时差为0.66μs。当信噪比分别为10 dB、-7.5 dB以及-25 dB时,站间接收信号的自相关和互相关函数比较如图4~图6所示。
图4~图6中,每个图的子图(a)表示完整观测时间内的相关函数,子图(b)表示相关函数最大峰值部分的放大示意图。可以看出,当信噪比为10 dB和-7.5 dB时,相关函数均有明显峰值,估计误差约为0.01μs,这个精度由采样率导致的数字时间间隔决定。当信噪比为-25 dB时,相关函数的最大峰值不再明显,而估计误差明显增大,上升约为之前的百倍。
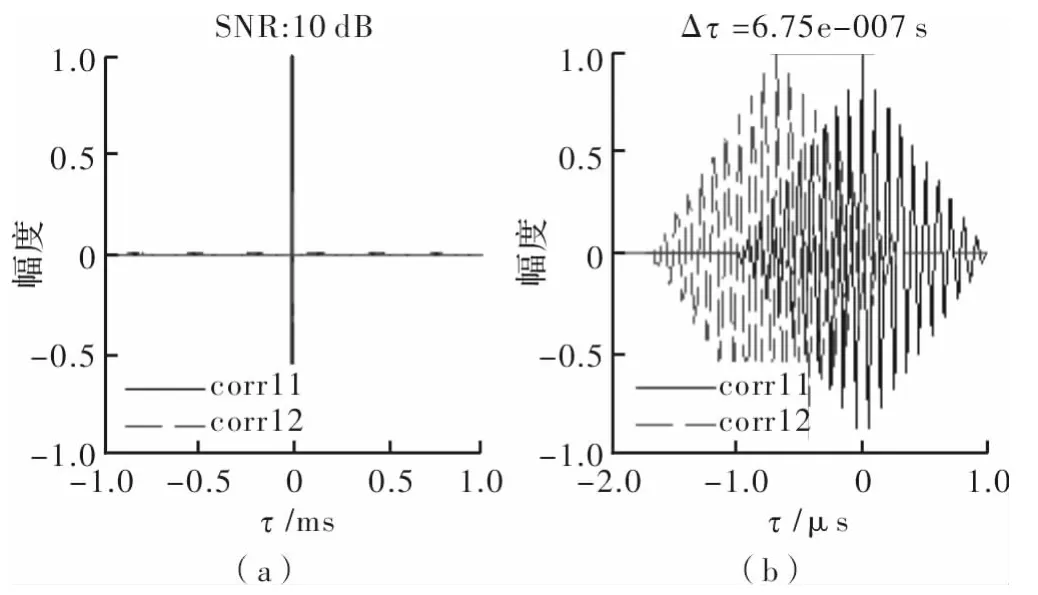
图4 SNR为10 dB时相关法估计误差
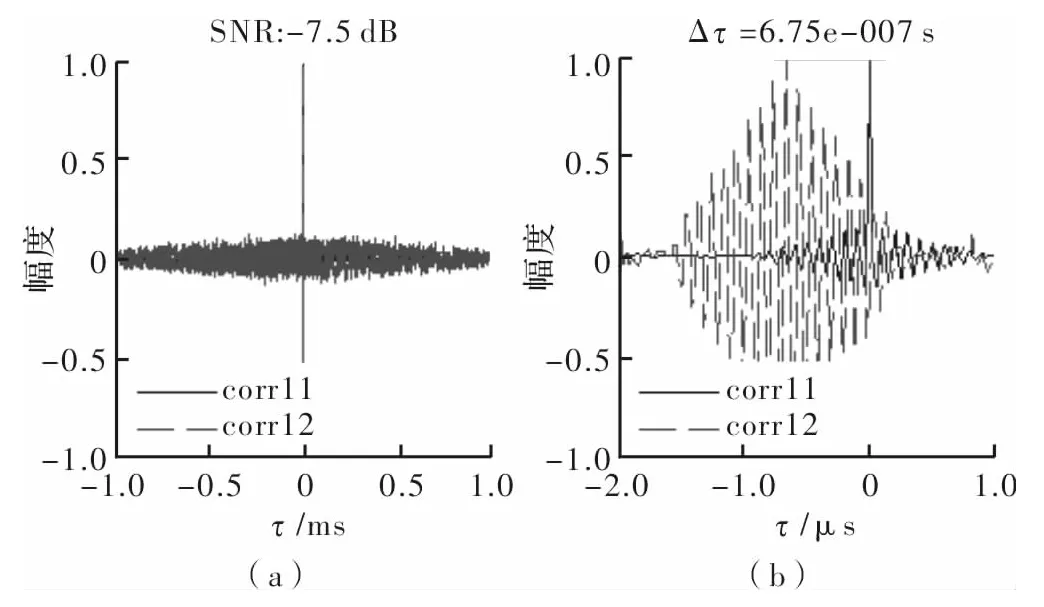
图5 SNR为-7.5 dB时相关法估计误差

图6 SNR为-25 dB时相关法估计误差
而当信噪比在-25~10 dB的范围内变化时,算法估计误差的变化规律如图7所示。
从图7中可看出,当信噪比小于一定门限时,估计误差会随着信噪比降低小幅提升,但总体上说,时差估计还是较为准确的。但当信噪比低过门限时,估计误差大幅上升,即可以认为此时出现了“跳周”误差。在此仿真环境中,“跳周”门限约在-17 dB。
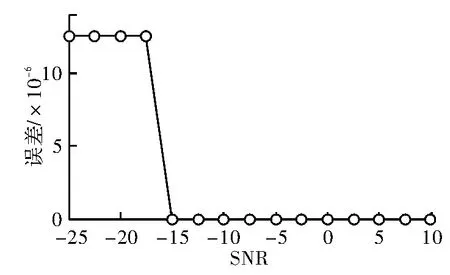
图7 不同信噪比对相关法估计误差的影响
保持仿真信号环境不变,且将信噪比控制在“跳周”门限内。当采样频率在范围内变化时,估计误差的变化情况如图8所示。
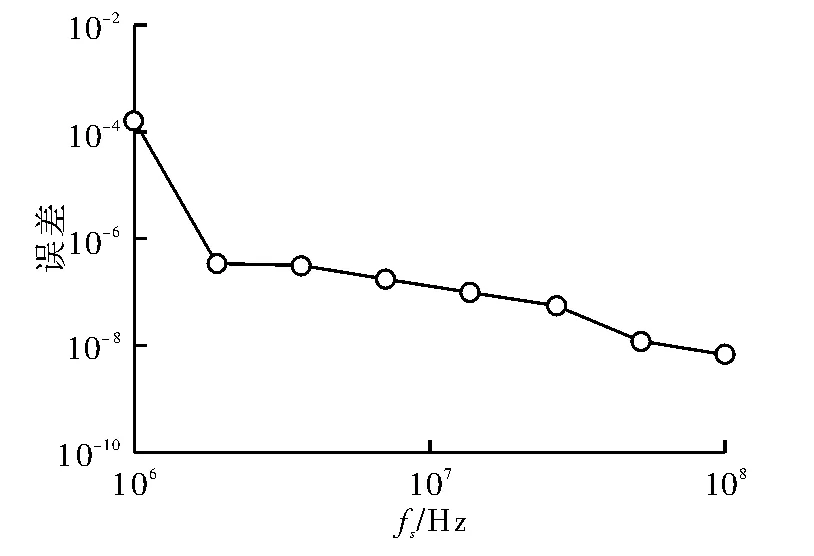
图8 不同采样频率对相关法估计误差的影响
图8是在完成400次独立重复实验后所得出的。从图中可看出,在信噪比门限内,时差估计误差大约和采样时间间隔在一个量级上。间隔越小,估计精度越高,但计算量也随之上升。
保持图8中的仿真环境,当站间多普勒频率差变化时,算法估计误差的变化情况以及校正多普勒频差后的估计误差变化情况如图9所示。
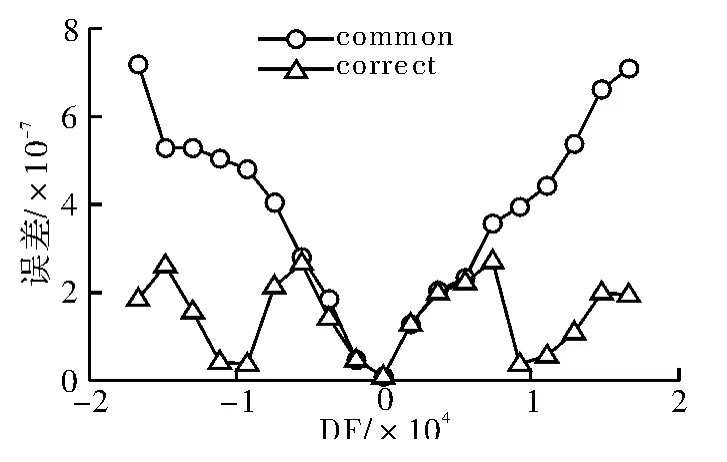
图9 相关法估计误差的多普勒校正
图9同样是在完成400次独立重复实验后得出的。从图中可看出,一般情况下估计误差与站间多普勒频差近似成正比。当经过多多普勒频率差校正后,估计误差不再随多普勒频差增大而增加,而是在一个相对较小的范围内震荡。
5 结束语
本文对TDOA定位技术中的时差相关估计算法进行了研究,并对其估计误差进行了分析。研究表明,理论上利用高频载波进行相关的估计算法具有较高的精度。由于利用了信号噪声不相关的特性,即使在信噪比较低的情况下,算法仍具有较高的精度。
而在实际运用中,算法精度更大程度上是由A/D采样率,即采样频率所决定的。时差估计精度和采样频率处在同一量级上。
同时还证明了多普勒频率对估计误差也有影响。在满足信噪比门限的情况下,估计误差和站间多普勒频率差近似的成正比。通过频域相关处理可校正该误差,并达到更好的估计性能。
[1]RICHARD A P.Electronic warface target location methods[M].UL USA:Artech House,2012.
[2]BJORKLUND S,LJUNG L.A review of time-delay estimation techniques[C].Paris:42nd IEEE Conference,2003:2502-2507.
[3] 徐捷,孟嘉,黄高明,等.欠采样条件下的正弦信号时差估计[J].航天电子对抗,2005,21(4):22-32.
[4]SO H C.Time-delay estimation for sinusoidal signals[J].IEEE Proceedings-Radar,Sonar and Navigation,2001,148(6):318-324.
[5]CARTER G C.Coherence and time delay estimation[J].Proc.IEEE,1987,75(2):236-255.
[6]MOGHADDAM P P,AMINDAVAR H,KIRLIN R L.A new time-delay estimation in multipath[J].IEEE Trans.Acoust.,Speech,Signal Processing,2003,51(5):1129-1142.
[7]YI M,WEI P,XIAO X C,et al.Efficient EM initialization method for time-delay estimation[J].Electronics Letters,2003,39(2):935-936.
[8]KNAPP C H,CARTER G C.The generalized correlation method for estimation of time delay[J].IEEE Transactions on Acoustics Speech and Signal Processing,1976,24(4):320-327.
[9] 金辉.广义相位相关用于时差估计技术研究[J].无线通信技术,2006(1):30-32.
[10]LIU Yueliang,JIANG Yuzhong,JIANG Wei,et al.Estimation algorithm of doppler shift and time delay in HF channel sounding[C].ICEMI,2011:350-354.

