圆形阵列天线在雷达中的设计及应用

林 晨，赵艳秋，陈舒敏

（船舶重工集团公司723所，扬州 225001）

0 引 言

在雷达及其它系统的许多应用中，需阵列天线具备在方位面进行360°扫描的能力。目前雷达系统广泛采用直线阵，通过合理布局直线阵可以实现这样的扫描，但增益和方向图等特性随扫描角的不同而改变。利用伺服系统，虽然保证了天线的性能，但却增加了额外设备，也给系统带来了数据率和稳定性下降的问题，这些限制了它们的实际应用。与之相比，圆形阵列具有良好的全方位扫描能力。圆形阵列由均匀分布在圆周上的天线单元构成。由于其内在的圆周旋转对称性，通过循环移动阵列激励，可简单而灵活地操控波束的方位，其增益和方向图等性能基本不变。同时，圆结构的对称性保持了单元间的互耦平衡，利于实际工程设计。

由于圆形阵的这些优势，很多学者加大了对其的理论研究［1－5］，使圆形阵得到日益广泛的应用。针对实际雷达系统，如何最大化发挥圆阵优势并克服其副瓣相对电平高的缺点［3－5］是值得探讨的问题。

1 基于圆形阵列的扫描方法

雷达系统要实现方位面内的搜索或跟踪功能，其天线需要形成扇形或针状波束且具备扫描能力。圆形阵列要能实现这样的功能，其阵列单元一般均匀分布在圆周上，方向图最大辐射方向为圆周径向。下面将基于上述背景条件，对圆形阵列的扫描方法进行讨论和分析。

1.1 单波束循环扫描方式

循环扫描方式是常见的一种圆阵扫描方法，即通过轮换各单元的加权矢量使波束在方位面内均匀地扫描。如图1所示，在半径为R的圆周上，均匀分布N个单元。当1～P号单元同时工作时（获得有效加权矢量），阵列形成波束1；关闭单元1，开启单元（P＋1），即2～（P＋1）号单元同时工作时，阵列形成波束2，依次类推，完成方位面“扫描”。当然，也可以控制其它连续P个单元天线，使波束指向所需的方位。

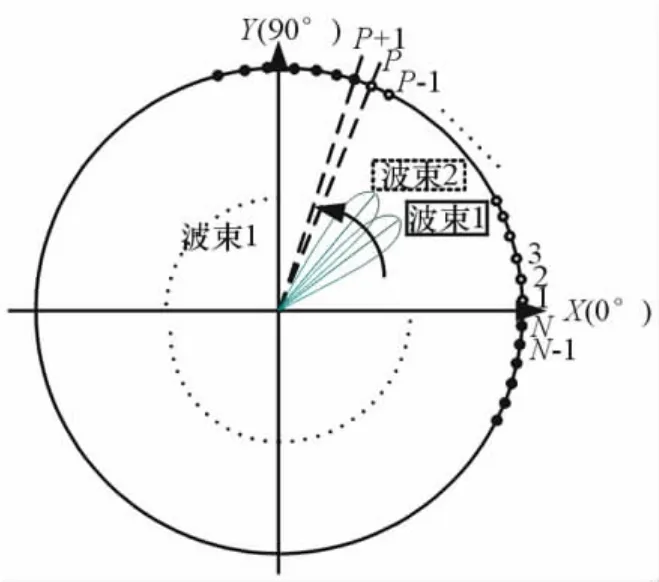
图1 单波束循环扫描方式示意图

值得注意的是波位间的波束指向间隔为2π／N，因此P个单元形成的主瓣波宽需稍大于扫描角度间隔才能保证方位面的完整覆盖，否则还需进行小范围内的电扫描。于此同时，为提高系统角度分辨率，需要P个单元形成较窄的波束，因此要完成对两者的兼顾需选择合适的单元总数N和同时工作的单元数P。

单波束循环扫描方式的最大优点在于维持了扫描过程中方向图和增益等的性能且波束控制灵活。但其存在阵面利用率和扫描数据率较低的缺点。

图2 多波束循环扫描方式示意图

1.2 多波束循环扫描方式

多波束扫描方式的工作原理与单波束方式基本相似，其不同点在于圆阵在同一个时刻产生2个或更多的波束。根据圆形阵列的结构特性可知，每个单元方向图的指向为径向，其半功率波束宽度小于180°，因此形成波束1－1所需共同工作的子阵数必然少于半个圆阵对应的子阵数。利用剩余单元至少可再获得一个性能相同的波束。如图2所示，圆阵同时产生2个反方向的波束1－1和2－1，2个波束的扫描工作方式相同，可实现同时向顺时针或逆时针方向0°～360°范围内的循环扫描。类似地，若实现方向图性能所需同时工作的单元数小于圆阵单元总数的1／3，则圆阵可同时形成3个波束。相对单波束方式而言，多波束扫描方式提高了阵面的利用率和扫描数据率，可使基于圆阵形式的雷达系统性能得到较大提高。

2 阵列方向图综合

多数关于圆形阵列综合的文献［1－4］都假设单元的方向图为各向同性，并假设单元间不存在互耦作用，但在实际的圆形阵列中，相邻单元的间距在0.5～0.7个波长之间，且每个单元的最大辐射方向均指向圆阵的径向。显然，实际阵列单元间存在着较强的互耦效应，因此这些文章所作的假设很粗糙，无法满足实际工程需要。通过对扫描方式的分析可知，雷达系统对圆阵中部分连续单元形成的方向图性能更为关心，因此基于阵中单元方向图并采用雁群粒子群算法（GPSO）［6］对圆阵中局部阵列方向图进行综合设计。

2.1 圆形阵列天线设计

圆形阵列天线结构见图3，半径R＝10.97λ，单元间距为0.5λ。单元采用印刷偶极子天线。

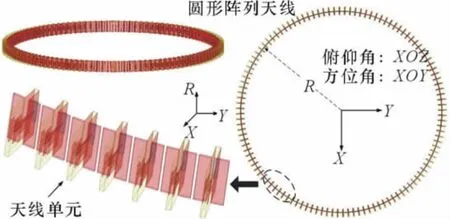
图3 圆形阵天线结构示意图

图4给出了单元天线在孤立环境和七单元耦合环境的方向图，可以看出耦合效应使单元方向图的形状及波束宽度变化明显。因此，采用阵中方向图可在考虑阵列互耦的情况下有效提高设计精度。

2.2 阵列方向图优化设计

2.2.1 优化模型

对圆阵上M个连续单元的方向图进行综合，其方位面内（θ＝90°）方向图可表示为：

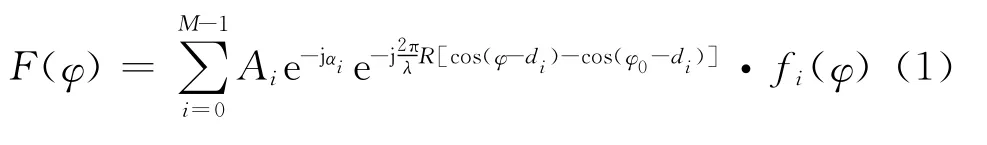
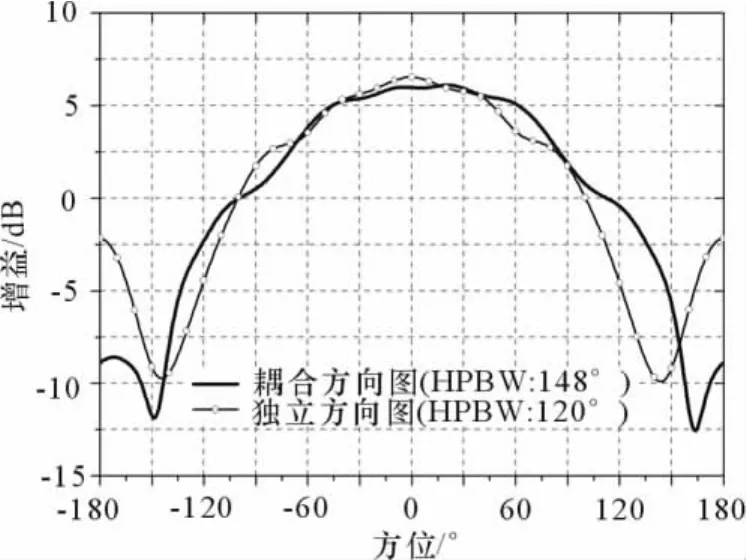
图4 单元方向图仿真结果

式中：Ai为第i个单元权重的幅值；αi为第i个单元权重的副瓣抑制相位；φ0为波束指向；d i为第i个单元的方位角；f i（φ）为单元阵中方向图。

对于同一个圆周上的不同单元，由于它们的相对位置具有圆周对称性，其耦合环境相同，因此它们的阵中方向图也具有一定的对称性，可以通过角度坐标平移相互变换。

采用GPSO优化算法，取相位－幅度为优化变量，令x＝ ［Ai｜αi］，在保证主瓣波宽的同时，优化最低的副瓣电平。其优化模型定义如下：

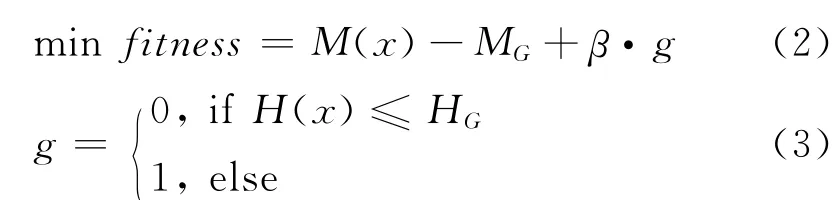
式中：MG为副瓣电平优化目标；H G为主瓣波宽优化目标；罚函数因子β＝1 000。

2.2.2 数值仿真

图5给出了圆阵中24个单元局部阵列未优化时的方向图，其主瓣波宽H＝4.5°，最大副瓣电平为－12.89 d B。

根据雷达系统的性能需求，对该阵列方向图进行优化。在GPSO优化算法中，种群个体数目设置为48，最大迭代次数为300，粒子维数为24，量化幅值Ai∈ ［0.6，1］，副瓣抑制相位αi∈ ［0，π／2］，H G＝5°，MG＝－20 dB。

图6给出了应用相位－幅度法，优化后的阵列方向图，其最大副瓣电平－22.10 d B，主瓣波宽5°，达到了设计指标要求。

3 结束语

基于雷达系统需求，结合圆形阵列天线的优点，分析了圆阵扫描方法的优缺点，其中多波束扫描方式在最大化发挥圆阵优势的同时具备了较高的效率，符合雷达发展的趋势。本文基于阵中单元方向图，采用GPSO算法对圆阵的局部阵列方向图进行了优化设计。通过对阵元幅度和相位的优化，使方向图在保持主瓣波宽不大于5°的条件下，副瓣电平低于－20 d B，达到设计指标要求。由于耦合单元方向图可通过仿真或测量获得，本方法同样适用于那些采用新型单元的阵列综合。该方法简单实用且灵活度高，可以很好地满足工程设计的需要。

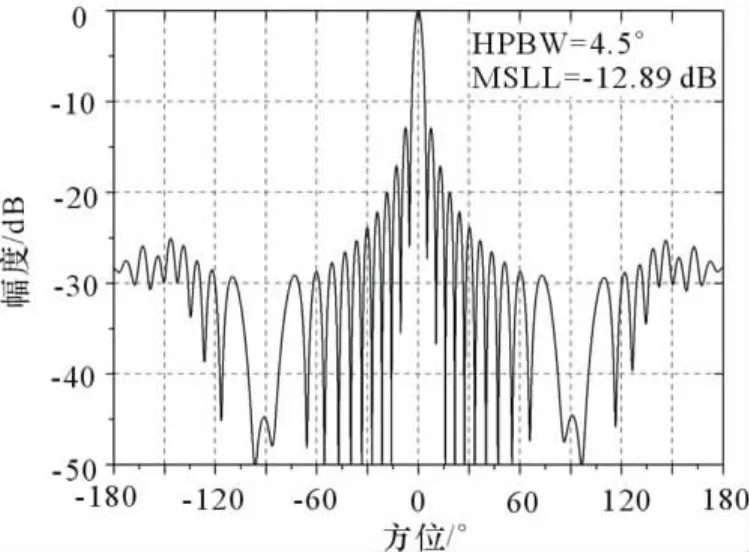
图5 优化前波束指向0°的方向图

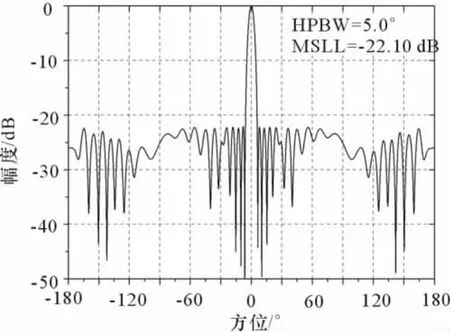
图6 优化后波束指向0°的方向图

［1］Vesuovo R.Constrained and unconstrained synthesisof array factor for circular arrays［J］.IEEE Transactions on Antenna and Propagation，1995，43（12）：1405－1410.

［2］Vesuovo R.Pattern synthesis with null constraints forcircular arrays of equally spaced isotropic elements［J］.IEE Proc－Micowave Antennas Propagation，1996，143（2）：103－106.

［3］刘先省，张连堂，吴嗣亮，等.基于有向阵元的圆形阵列方向图综合［J］.电子学报，2004，32（4）：701－704.

［4］刘先省，张连堂，周林.给定方向图的圆形阵列综合方法［J］.电子学报，2005，33（2）：245－248.

［5］包子阳，陈克松，何子述，等.基于EDA的圆阵旁瓣电平优化方法［J］.雷达科学与技术，2008，6（4）：311－314.

［6］刘金洋，郭茂祖，邓超.基于雁群启示的粒子群优化算法［J］.计算机科学，2006，33（11）：166－168.