IEC60060-1Ed3.0中雷电波形处理方法的研究*
李文婷 刘少波 龙兆芝 雷 民 宗贤伟 刘高佳
(中国电力科学研究院计量研究所,武汉 430074)
0 引言
冲击电压测量为高压测试中十分重要的一项,目前使用的冲击测量系统大都能满足实际使用需求,但随着IEC60060-1:2010 ED.3.0[1]中对带过冲和振荡的雷电冲击波形处理方法的修改,调整冲击测量系统中雷电全波的测量处理方法是亟待解决的问题。为此,我们进行了这方面的研究工作。
1 冲击测量处理程序
完整的冲击测量系统如图1所示:冲击发生器产生的冲击电压经过冲击分压器,通过分压器的测量电缆传输到示波器(或者数字采集卡),示波器再与计算机相连将测量数据导入到二次测量分析软件中计算分析,输出冲击波形各参数。

图1 冲击测量系统原理框图
目前常用的冲击处理程序都是依据IEC60060-1 Ed 2.0[1]中的处理要求编制,并通过对IEC61083中附带的TDG(波形发生器)中波形的测量结果来验证软件的计算精度是否满足要求。
IEC60060-1Ed3.0于2010年颁布,与IEC60060-1Ed2.0中对带振荡雷电波的处理方法有较大不同,其中Ed2.0中对雷电波的处理办法为:
1)对于振荡频率不小于0.5MHz或者过冲持续时间不大于1μs的实测雷电波形,取波形的平均曲线作为试验电压波形。
2)对如果频率小于0.5MHz或者持续时间大于1μs的实测波形,则将原始波形直接作为试验电压波形求取参数。
上述处理方法中存在的争议主要在于波形平均曲线的定义较为模糊,在实际测量中很难处理;以0.5MHz作为分界频率,并不符合实际应用中的所有情况。因此,在IEC60060-1Ed3.0中,对带振荡和过冲的雷电波形的参数处理,引入了试验电压因子k(f)(f为振荡频率),利用该试验因子对雷电波形中的振荡部分进行滤波处理。该试验电压因子的提出是基于大量研究者针对带过冲和振荡雷电冲击电压的振荡频率对各类绝缘击穿实际影响的试验研究结果[2-3],研究表明振荡频率对绝缘试验中击穿电压的影响是随着频率渐变的,引入试验电压因子k(f)能更加准确的反映不同频率的振荡对绝缘击穿电压的影响,对实际冲击测量有重要意义。
2 带过冲和振荡雷电全波及雷电截波波形处理
IEC60060-1Ed3.0中引入试验电压因子k(f)后,给出的待确定的雷电波试验电压值Ut的计算公式为:
Ut=Ub+k(f)(Ue-Ub)
(1)
式中,Ub为拟合基准曲线的最大值;Ue为原始记录曲线的最大值;k(f)为试验电压因子。
在程序处理过程中,需要根据原始记录曲线确定拟合基准曲线,并构建试验电压因子k(f)对原始记录曲线中除去拟合基准曲线后的剩余曲线波形进行滤波,最终求取试验电压值。
IEC标准中只给出了上述计算过程的基本步骤,而在程序的实现过程中尚存在一些难点,如波形起始点的确定,曲线拟合及滤波器构造,雷电截断波波尾截断点确定等,下文将对这些难点进行论述。
2.1 雷电全波处理方法的实现
2.1.1 波形平坦部分起始上升点的确定
通过测量仪器记录到的雷电波形数据,首先要确定记录波形的起始上升点,确定好波形的起始上升点后,才能确定记录曲线的基准水平,从而对波形进行后续处理。
通过分压器实际测量得到的雷电冲击波形的起始部分通常是充满褶皱的近似平坦曲线,因此,确定波形的起始上升点较为困难。虽然波形起始点的确定方法有较为详细的介绍[4],但笔者按照该方法处理时发现,采用该方法对实测波形的平坦部分有一定要求,如当实测波形起始部分振荡严重或实测波形起始部分受干扰严重时,处理程序会陷入死循环,无法确定波形起始点。鉴于这种方法存在的缺陷,本处理程序中采用了一种新的处理方法:对于数据采集装置采集的波形数据,首选确定波形的极值点P,然后从该极值点向该点之前对应时间的点搜索,直到找到一个点A与波形初始点O的幅值差和极值点P与波形初始点A的幅值差之间的比例的绝对值小于某个足够小的值a(a可取值在0.001~0.005之间),那么该点A即可认为是平坦部分截止点,如图2所示,即若|UA-Uo|≤a|UP-UA|时,则A点可确定为平坦部分截止点或称为波形上升起始点。
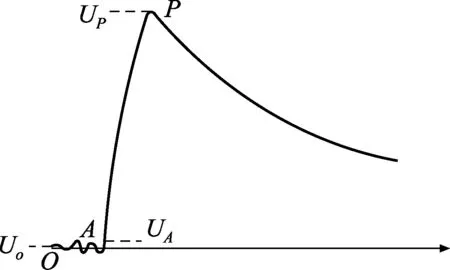
图2 波形起始点的确定
采用这种方法确定波形起始点在Labview中实现较为简单,且对实测的波形起始部分没有限制,在实测波形中干扰较大时也可以适用,经实测发现此方法确定的波形起始点计算速度快,完全满足后续计算精度的需求。
确定了波形的起始上升点后,取起始上升点之前的N个点计算这些点幅值的平均值,求取记录曲线的基准水平,从而确定记录波形的偏置补偿记录曲线U0(t)。
2.1.2 雷电波基准曲线拟合
依据IEC60060-1中对雷电波形的处理要求,取雷电压波偏置补偿曲线U0(t)中波前0.2Ue(Ue为记录波形偏置补偿曲线的最大值)幅值点至波尾部分0.4Ue幅值点之间的所有数据点,按照给定的函数模型进行曲线拟合,得到拟合雷电波基准曲线。IEC60060-1Ed3.0中给出的拟合曲线的函数模型为
Ud(t)=U[e-(t-td)/t1-e-(t-td)/t2]
(2)
该函数模型为4参数曲线拟合模型,4个自由参数为:曲线的极限值(U)、多次拟合试验后给出的最佳拟合初始设定值(t1、t2)和曲线的实际原点或视在原点(td),本测量软件采用LabView中曲线拟合模块来进行曲线拟合。拟合中设置4个参数初始假定值可以缩短计算时间,将上述4参数按照IEC60060-1Ed3.0中给定的假定值进行设定:U:实际测量时根据实际记录曲线的峰值电压点进行设置;t1:70μs;t2:0.4μs;td:实际处理时按照实际记录曲线的实际原点进行设定。
在程序中依据该假定值进行初始设置后,计算结果可以较快收敛,给出符合当次测量波形的曲线拟合值。曲线拟合完成后,即可确定所记录雷电波形的基准曲线Um(t),从偏置补偿记录曲线U0(t)中减去基准曲线Um(t)以获得剩余曲线R(t)=U0(t)-Um(t)。
2.1.3 试验电压因子k(f)
IEC60060-1Ed3.0中提出了对剩余曲线进行滤波的试验因子k(f),该试验因子可以理解为为了求取试验电压值,基于过冲频率的幅值衰减因子。图3为相关学者根据大量实验得到的数据点拟合的k(f)的近似曲线,该曲线的公式为k(f)=1/(1+2.2f2),图3中折线为IEC60060-1Ed2.0中以0.5MHz为绝对界限处理振荡波形的电压因子。
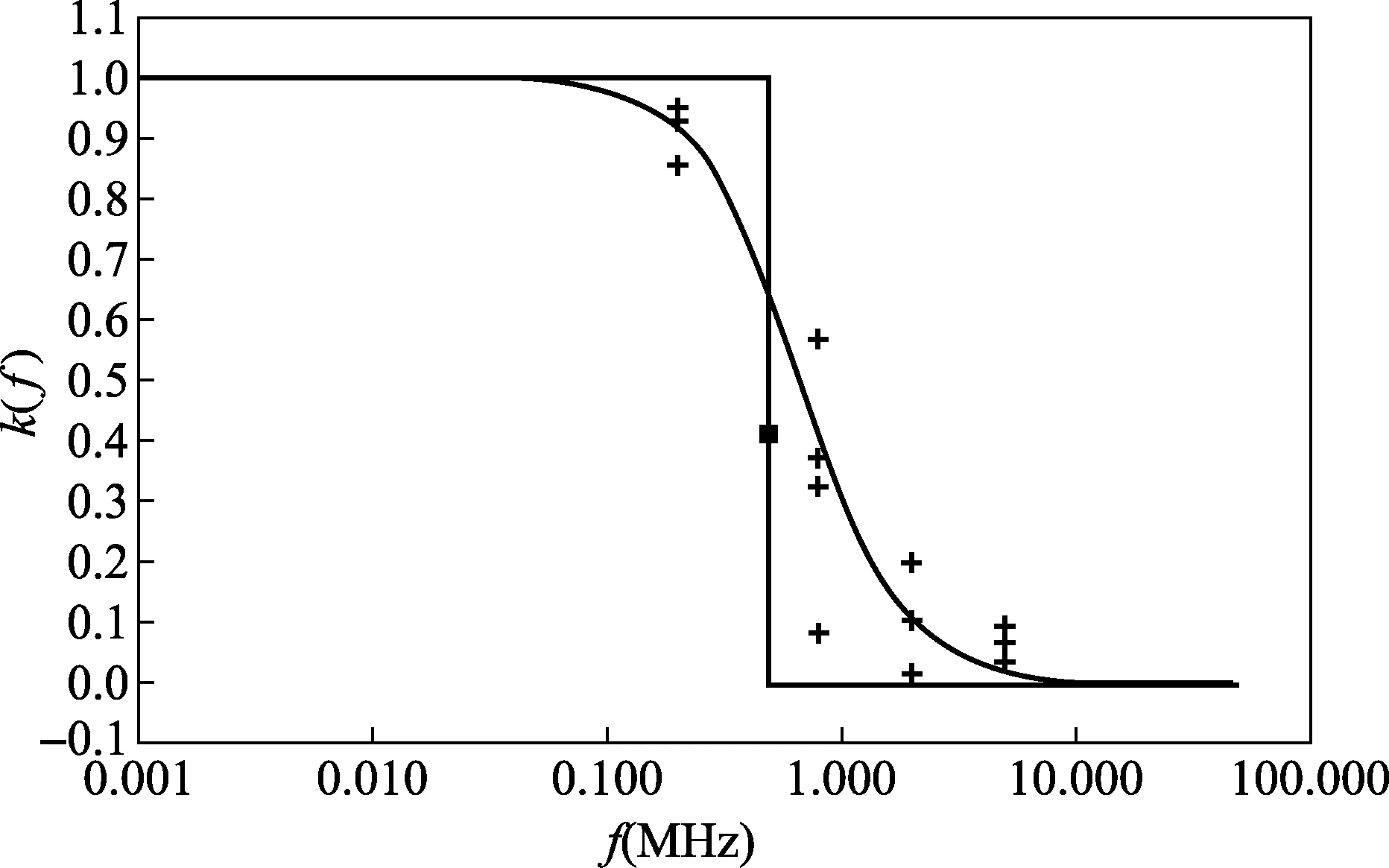
图3 k(f)曲线图
在雷电波处理程序中,实现该试验因子的功能需构建一个传递函数为k(f)的数字滤波器。IEC60060-1Ed3.0中附录C中给出的滤波器创建的公式为:
y(i)=b0x(i)+b1x(i-1)+a1y(i-1)
(3)
b0=b1=x/(1+x)
(4)
a1=(1-x)/(1+x)
(5)
(6)
其中,a=2.2×10-12(K因素滤波器的-3dB点);Ts为记录信号时使用的采样间隔;x(i)为滤波器的输入采样排列(电压);y(i)为滤波器的输出采样排列。
依据式(3)~式(6),在LabView中构建的滤波器为基于正向计算的零相位IIR(有限冲击响应)滤波器,该滤波器的衰减仅为实际所需衰减的一半。因此,在波形处理时,剩余曲线波形数据通过该滤波器的次数为两次,先正向后反向,这样可以达到实际滤波衰减的效果,同时还可以消除相位漂移,顺利的完成雷电波形剩余曲线的滤波。
2.2 波尾雷电截波波形处理
除了雷电全波测量处理外,雷电波尾截断波形的处理也较复杂。本处理程序中采用有序样本均值聚类[5-7]的分析方法确定雷电波的截断瞬间,均值聚类分析方法的基本思想是把各类事物的均值看做该类的“类中心”,通过建立合适的分类目标函数,对目标函数取最大值或最小值,可以确定两类之间的界限点。
对于雷电波波尾截断点的确定,把采集到的波形数据点分为两类:截断点前一类和截断点后一类,在具体处理中把峰值点到截断点分为一类,截断点到波形过零点作为一类。
设一段由数字示波器得到的雷电冲击截波采样序列,共M个采样点:x1,x2,…,xM,采用均值聚类分析方法时,把M个采样点看成二维空间向量,则定义采样点序列中的两点A(x1,x2),B(y1,y2)之间的距离D(x,y)为:
或
(7)
定义分类中两类的类中心:
Γk:bk=(bk1,bk2)k=1,2
(8)
(9)
同时定义一个采样点与一个类之间的距离就是该采样点与该类的类中心的距离:
DL(x,Γk)=DL(x,bk)
(10)
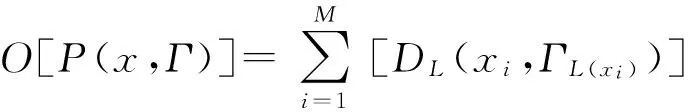
在本截断点寻找的试验中,为了加快搜寻速度,选取的分类总体是波形极值点与波尾为极值点幅值0.1倍的点之间的所有点。从波形极值点开始作为假设的截断点,再将极值点与该“截断点”(假设的)之间的所有点的电压幅值求均值,该均值作为假设“截断点”之前的类的类中心A,将假设“截断点”与波后为极值点0.1倍的点之间的所有点的电压幅值求均值,该均值作为假设“截断点”之后的类的类中心B。假设“截断点”与类中心A间的幅值差绝对值即为该点与该类的距离,该假设点与类中心B间的幅值差绝对值即为该点与该类的距离。两绝对距离之和为假设的“截断点”(即分类点)与两类点之间的误差,真正的截断点(分类点)与两类的之间的误差最小。
在Labview中依据上述思想编制程序,确定与两个分类中心的距离之和最小的点为截断点,通过测试给定参考值的波形,测试结果表明程序确定的截断点准确可靠,满足标准精度的要求。
3 TDG波形测量结果分析
为了验证该测量处理程序计算带振荡雷电全波的准确性,笔者利用该处理程序对IEC61082-2Ed2.0:42/271/CD[8]中附带的试验波形发生器TDG2.06中所列出的雷电全波LIA1-LIA12波形进行了测试。表1中列出了该冲击计算处理程序的测量结果,表2中列出了波形参考值的扩展不确定度及各波形测量结果与给定参考值的偏差,并依据IEC61083-2Ed2.0中附录B的要求对采用该雷电波计算处理程序测量冲击电压峰值时的测量不确定度进行了分析:
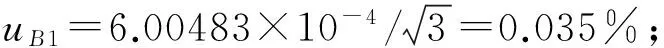
=0.036%
则当该冲击处理程序应用到冲击电压测量系统中时,由该数据处理程序引入的标准不确定度为0.036%。
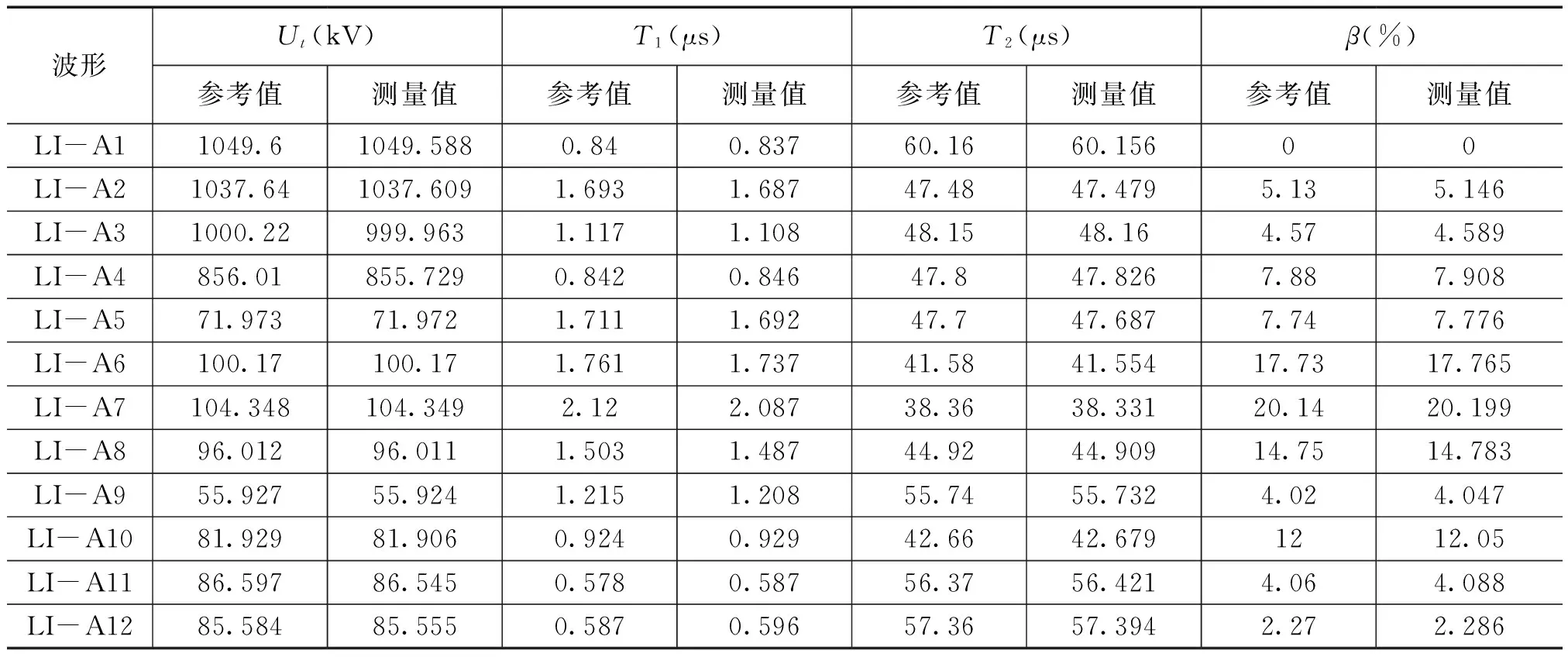
表1TDG2.0.6中雷电压全波测试结果
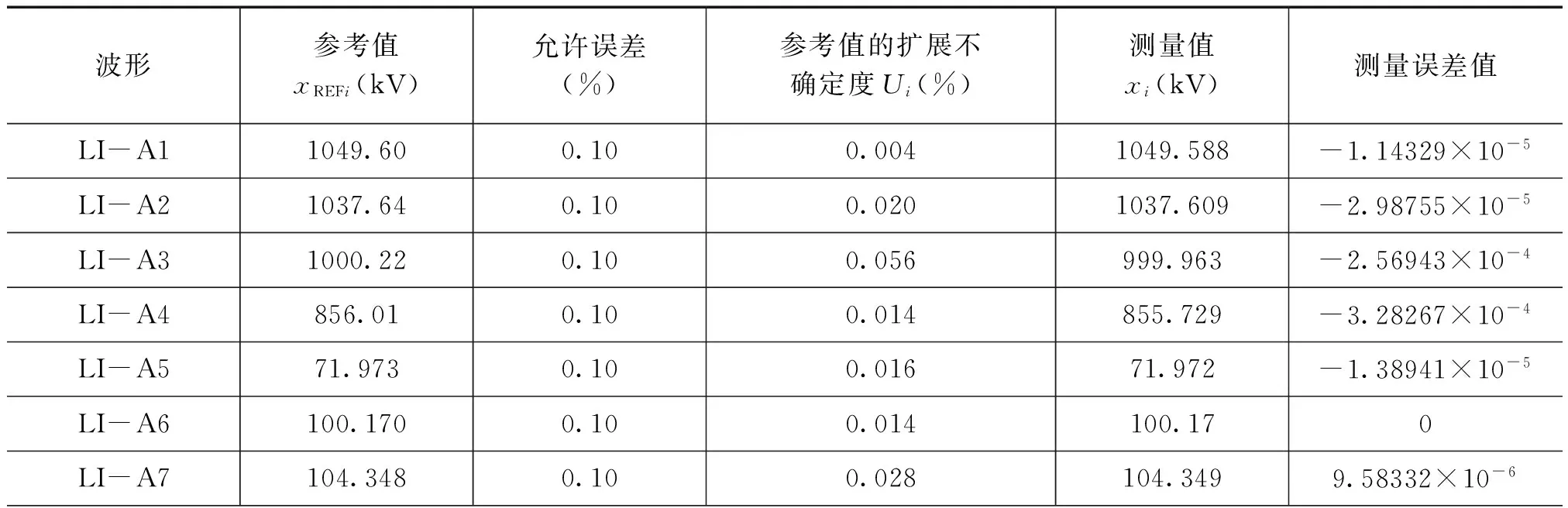
表2雷电压全波峰值测量不确定度计算
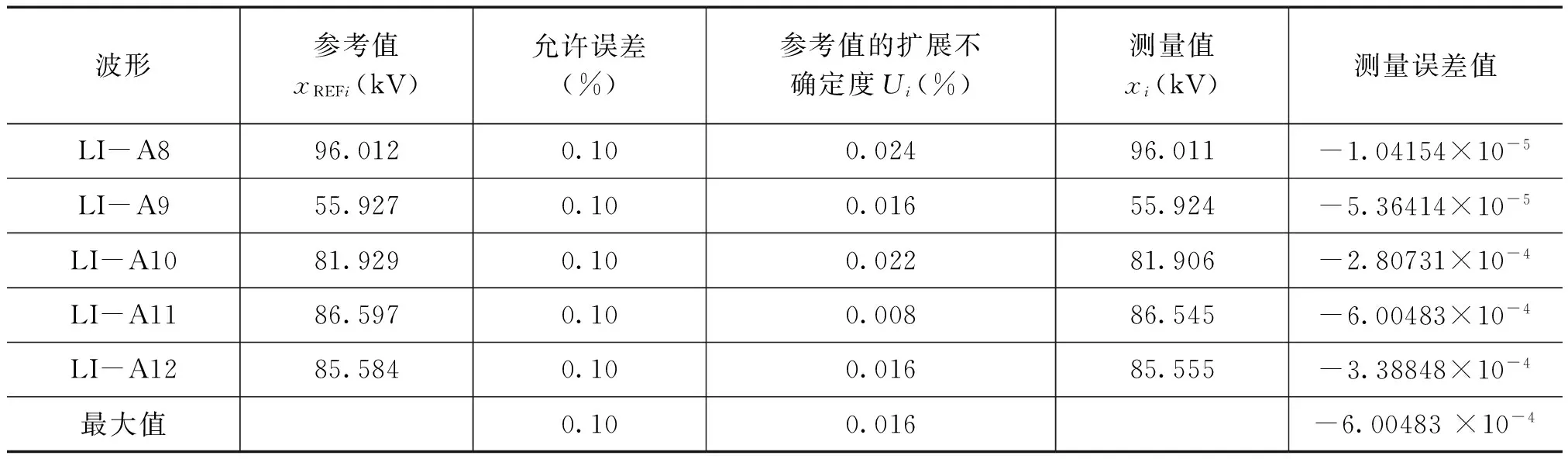
续表
4 结论
依据IEC60060-1Ed3.0中对于雷电波形处理的新要求编制了新型冲击测量处理程序,介绍了在Labview中实现雷电冲击全波测量处理及波尾截断雷电波的处理方法。利用该测量处理程序对TDG2.0.6中的雷电全波进行测试,并对该处理程序测量雷电全波峰值时引入的测量不确定度进行了分析,测量结果表明该二次测量系统的分析计算精度完全满足IEC60060-2[9]及IEC61083-2中对冲击测量处理软件计算精度要求。
该计算处理程序与示波器(采集卡)等配套使用可以保证冲击二次测量系统的的准确度,对于冲击电压计量,研究有重要意义。
[1] International Standard IEC60060-1.High-Voltage Test Techniques.Part 1:General definitions and test requirements [ S ] .3 rd ed .,Geneva,Switzer-land,2010
[2] HALISTORM,J,BERLIJN S,GAMLIN M,et al.Applicability of Different Implementations of K -factor Filtering Schemes for the Revision of IEC 60060-1 and-2.[C].Beijing ISH,2005
[3] 李晨光,张文,刑海瀛,等.新型高电压冲击测量系统研究[J].中国农村水利水电,2011(3)
[4] 郭弘,吴鹏,郭治峰,等.带过冲和振荡雷电冲击波形的参数提取研究[J].高压电器,2010,46(1)
[5] 赵刚,朱旭东,陈文针.雷电冲击截波截断瞬间确定方法研究.高压电器,1999(5)
[6] 南京大学数学系计算数学专业编.概率统计基础和概率统计方法.北京:科学出版社,1979
[7] 肖如芸.概率统计计算方法.天津:南开大学出版社,1994
[8] IEC61083-2Ed2.0:42/271/CD.Instruments and Software Used for Measurement in High-voltage Impulse Tests[S]
[9] International Standard IEC60060-2.High-Voltage Test Techniques.Part 2: Measuring systems [S].3 rd ed .,Geneva,Switzer-land,2010

