电离层侧向散射传播特性分析

李铁成 蔚 娜 李 雪 王世凯 郭文玲

(中国电波传播研究所，山东 青岛 266107)

引 言

电离层的特性决定了以它作为传输媒质的系统，必须配备电离层诊断系统，实时进行电离层探测. 比较成熟且已在实际工程中应用的地基电离层探测技术主要有垂测[1]、斜测[2]和返回散射探测[3-4]技术，而侧向散射探测技术是近几年新兴的电离层探测技术.

所谓侧向散射，其传播过程为：发射站发出的无线电波经电离层反射到远方地(海)面，后经地(海)面散射，发生非后向散射的“侧向”传播，再次经电离层反射到达远离发射站的地方被接收到[5-6]. 侧向散射探测时，接收站接收到的侧向散射来波信号相当于由接收波束内的地面上无数个连续分布的应答器转发的信号组成. 如何基于电离层侧向散射探测结果准确获取探测区域内电离层状态信息，并应用到实际工程中去，还需要对电离层侧向散射传播特性深入研究.

目前，国内外关于侧向散射方面的研究报道比较少见，文献[7]初步合成了侧向散射电离图，文献[8]介绍了开展的侧向散射探测试验，在国内首次获得了侧向散射信号的群距离-多普勒谱图、侧向散射扫频电离图. 为了对侧向散射传播特性有更深入的分析，本文基于雷达方程，推导了侧向散射来波信号的信噪比方程，并利用三维数字射线追踪技术[9]，合成了不同接收波束指向下的侧向散射扫频电离图，分析了最小时延线、不同地面距离最大可用频率(MUF)等参数的变化规律.

1 来波信号信噪比方程

为了得到侧向散射探测信号，发射站和接收站之间间隔较远的距离是有必要的. 因此，接收站接收到的信号包含两部分，一部分是由发射站发出经电离层反射后直接被接收站接收的斜测信号，另一部分是由发射站发出经电离层反射到远方地(海)面，经地(海)面散射后，再次经电离层反射被接收站接收到的侧向散射信号. 虽然，斜测信号不属于侧向散射信号，但它是侧向散射探测结果的一部分，所以文中也给出了斜测信号的信噪比方程. 下面分别推导这两部分信号的信噪比方程.

1.1 斜测信号信噪比方程

从发射站发射的无线电波经电离层反射后传播到接收站处的功率密度ρ为

(1)

式中：Pav为平均发射功率；Gt为发射天线增益；R为发射站到接收站天波传播群距离；La为电离层吸收损耗.

假设接收天线有效接收孔径为Ae，则接收到的信号功率为

(2)

考虑外部噪声功率N为

N=kT0FaB.

(3)

式中：k为玻尔兹曼常数；T0为接收站等效噪声温度；Fa为噪声因子；kT0Fa为每赫兹外噪声功率；B为信号带宽.

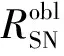
(4)

式中：τ为线性调频脉冲宽度；M为相干积累次数.

1.2 侧向散射信号信噪比方程

从发射站发射的无线电波经电离层反射后传播到散射单元处的功率密度ρ1为

(5)

式中：R1为发射站到散射单元天波传播群距离；La1为相应路径电离层吸收损耗. 则由散射单元辐射的无线电波信号功率为

Pt2=ρ1σ.

(6)

式中σ为散射单元雷达散射截面(Radar Cross Section, RCS).

从散射单元辐射的无线电波信号经电离层反射后到达接收站的功率密度ρ2为

(7)

式中：R2为散射单元到接收站天波传播群距离；La2为相应路径电离层吸收损耗.

则接收站接收到的信号功率为

(8)

(9)

2 仿真参数计算方法

2.1 侧向散射信号路径参数

在返回散射传播中，通常假设，发射站到散射单元和散射单元到接收站电波经历了相同的传播路径，而对侧向散射，由于收发站位置不同以及电离层的不均匀性，发射站到散射单元和散射单元到接收站电波必定经历了不同的传播路径，因此，侧向散射信号路径参数计算也相对复杂一些. 基本步骤是：

1) 基于电离层模型，运用三维数字射线追踪技术，分别获得以发射站(接收站)为中心，发射波束(接收波束)内以一定间隔步进的方位角上电波传播路径的主要参数如群距离、地面距离、射线仰角、反射层标志等，将地面距离以一定间隔划分成网格，对群距离、射线仰角等按照地面网格进行插值.

2) 发射波束内的发射方位角上，根据获得的电波传播路径的地面距离确定所有散射单元的位置(经纬度信息)；对所有散射单元，计算其对应的接收方位角，保留处于接收波束内的散射单元.

3) 对于保留的散射单元，分别计算其到接收站的地面距离，查找对应接收方位角内电波传播路径中是否包含该地面距离，如果包含，则认为该条侧向散射路径存在.

4) 记录侧向散射路径参数，主要包括：散射单元位置、发射仰角、发射站到散射单元电波传播群距离和反射层标志、散射单元到接收站电波传播群距离和反射层标志、接收仰角.

2.2 电离层吸收损耗

电离层吸收损耗按式(10)计算[5]

(10)

式中I为吸收指数，且

I=(1+0.0037R12)[cos(0.881χ)]1.3.

(11)

式中：R12为太阳黑子数12个月的流动平均值；χ为太阳天顶角，根据月份、地理位置与地方时可由式(12)计算

cosχ= sinXnsinSx

+cosXncosSxcos(Sy-Yn).

(12)

式中：Xn为反射点的地理纬度；Yn为反射点的地理经度；Sx为太阳视赤纬月中值；Sy为太阳直射点的经度；Sy=15ty-180，ty为世界时；i100为电波入射角(高度100 km处)；f为电波频率,MHz；fH为磁旋频率,MHz.

3 仿真结果分析

3.1 仿真条件

1) 电离层相关参数：

电离层模型采用分段准抛物(Quasi-parabolic segments,QPS)电离层模型，考虑包含E层和F层的情况，参数为：

第一组：

E层：fcE=5.9 MHz，rbE=90 km，ymE=20 km

F层：fcF=9.5 MHz，rbF=180 km，ymEF=80 km

第二组：

E层：fcE=3 MHz，rbE=90 km，ymE=20 km

F层：fcF=8 MHz，rbF=200 km，ymF=100 km

其中，fcE和fcF、rbE和rbF、ymE和ymF分别为E层和F层的临界频率、底高、半厚度.

电离层吸收损耗计算用参数：考虑时间为2011年6月某天上午9点(北京时)，则R12=53，Sx=-0.035 5，ty=1，fH=1 MHz.

2) 系统相关参数为：

收发站位置参数：发射站在接收站北偏东约50°方向上，相距1 187 km，布局如图 1所示；

发射功率：Pav=50 kW；

发射天线：全向天线，Gt=11.5 dB；

接收天线：方向性天线，Gt=9.5 dB，主波束宽度为1°，分别指向60°、90°、120°、150°和180°(以正北方向为基准，顺时针旋转)，如图 1所示；

系统损耗：Ls=12 dB；

波形参数：τ=50 ms，B=10 kHz，M=256；

环境参数：kT0=-204 dB，Fa=30 dB.

3) 为了比较不同接收天线指向时侧向散射电离图的变化情况，散射单元RCS均取20 dB.

图1 收发站布局示意图

3.2 结果分析

采用第一组电离层参数，图2～6给出了接收天线不同指向时仿真得到的扫频电离图，此时图中能够看出有多种电离层传播模式(EE模式(第一个字母表示发射站到散射单元的传播模式，第二个字母表示散射单元到接收站的传播模式)、EF模式、FE模式和FF模式)，不同传播模式混叠到一起，但各传播模式的最小时延线(“前沿”)能够明显区分.

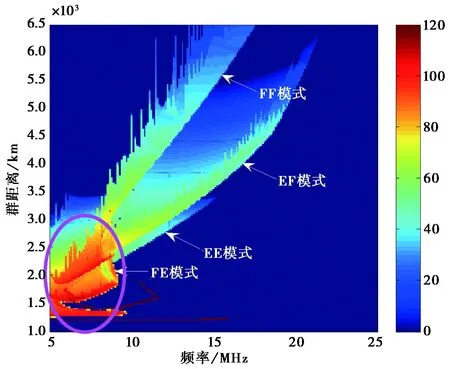
图2 侧向散射扫频电离图(接收波束指向60°时)

图3 侧向散射扫频电离图(接收波束指向90°时)

图2和图 3中，在低频处能够看到较强的来波轨迹(如图中椭圆框内所示)，这主要是因为此时散射单元距离接收站比较近，散射单元到收发站之间的夹角(简称“夹角”)相对比较大，发射站到散射单元和散射单元到接收站的群距离相对较小，路径损耗比较小，所以对应散射单元的来波信号能量比较强.

图7给出了不同波束指向时夹角随地面距离(距离接收站)的变化情况，图 8给出了不同波束指向时不同地面距离上来波(FF模式)的群距离-频率轨迹图. 比较两幅图，不难得出，当夹角比较大时，对应散射单元处MUF(发射站到散射单元再到接收站的MUF)会偏离最小时延线，随着夹角的减小，MUF与最小时延线上的点迹重合. 图 8中，随着波束指向从60°变到180°，来波覆盖区先变大再变小，接收波束指向120°时，可以看到明显的高低角射线组合，其中T表示发射站到散射单元的射线，R表示散射单元到接收站的射线.

图5 侧向散射扫频电离图(接收波束指向150°时)

图6 侧向散射扫频电离图(接收波束指向180°时)

图7 不同波束指向时夹角随地面距离的变化情况

图9给出了不同波束指向时最小时延线的变化情况，结合图 10所示的最小时延线上散射单元对应夹角的变化情况，可以看出，对于EE、FF模式，某一固定频率，夹角越大，最小时延越小，夹角越小，最小时延越大. 对于EF、FE模式，最小时延和夹角的关系不是那么明显，随着接收波束指向从60°变到180°，EF模式的最小时延对应的频率有减小的趋势，而FE模式则有增大的趋势.

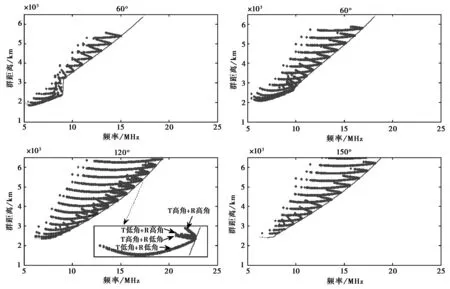
图8 不同波束指向时不同地面距离上来波的群距离-频率轨迹图

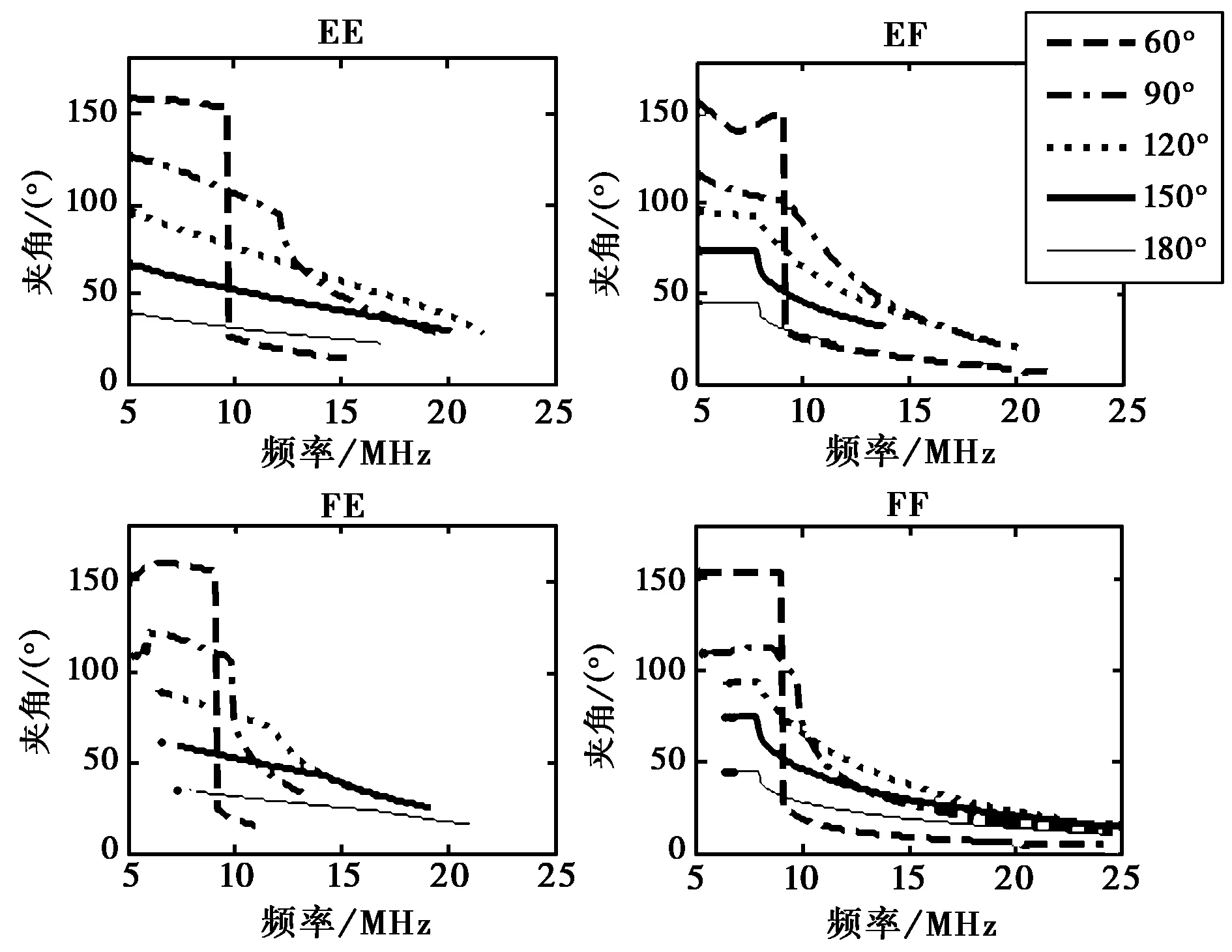
图10 最小时延线上散射单元对应夹角的变化情况

图11给出了不同波束指向时不同地面距离(距离接收站)MUF的变化情况. 一般情况下，对于某一固定传播模式，随着地面距离的增大，其对应的MUF也会相应的增大(当然，不会无止境的增大). 但从图 11中可以看出，当接收波束指向60°和90°时，MUF并不是单调递增的，这主要是由散射单元的地理位置决定的. 结合图 7，当接收波束指向60°和90°时，随着散射单元距离接收站地面距离的增大，夹角起初为钝角，逐渐减小，变为锐角后，继续减小，根据几何关系可知，发射站到散射单元的地面距离会先减小再增大，当减小程度大于散射单元到接收站的增大程度时，就会出现图 11中MUF减小的情况.

图12～14给出了采用第二组电离层参数时得到的不同波束指向时最小时延线、不同地面距离MUF等的变化规律，与第一组电离层参数得到的结果基本一致.

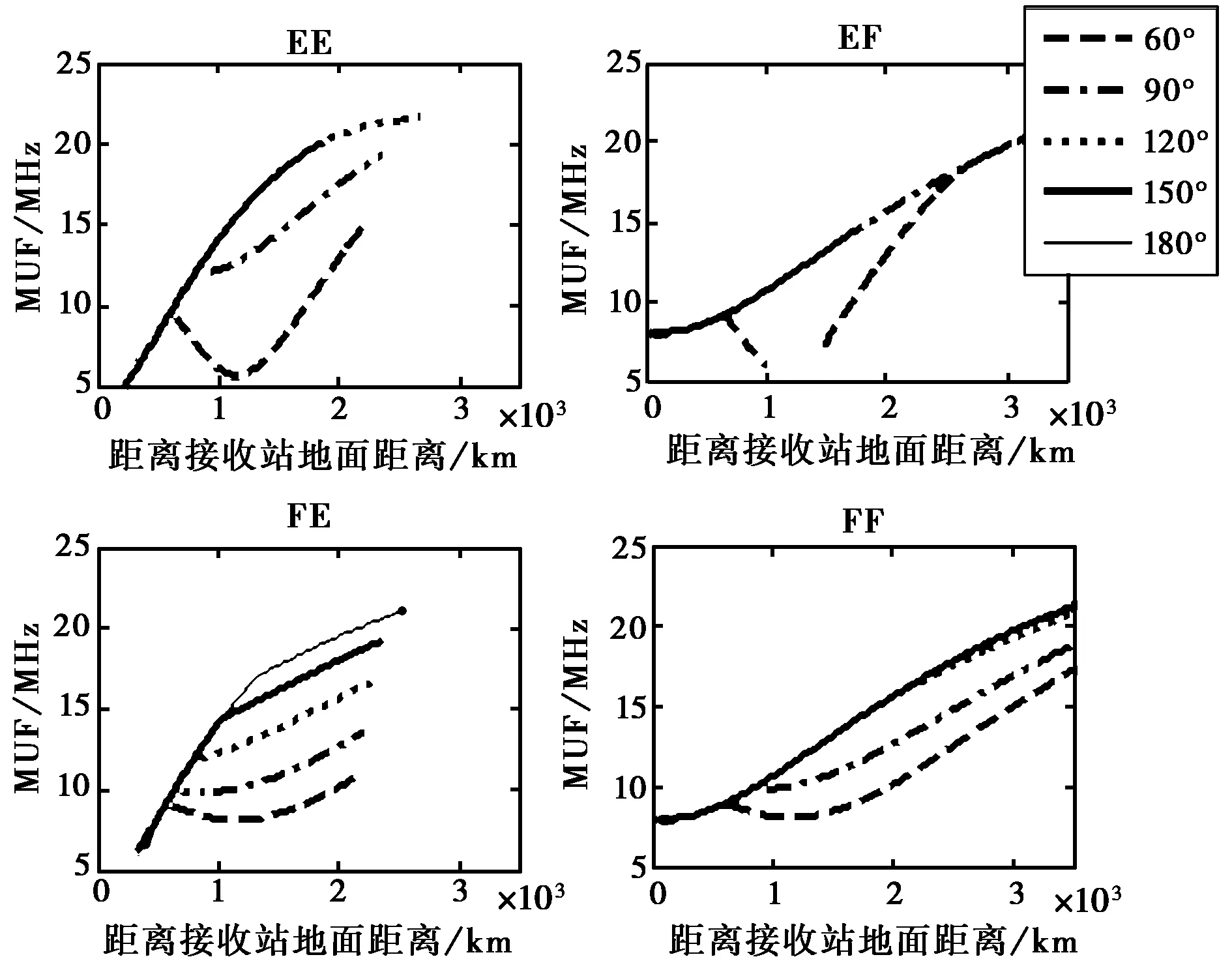
图11 不同波束指向时不同地面距离MUF的变化情况

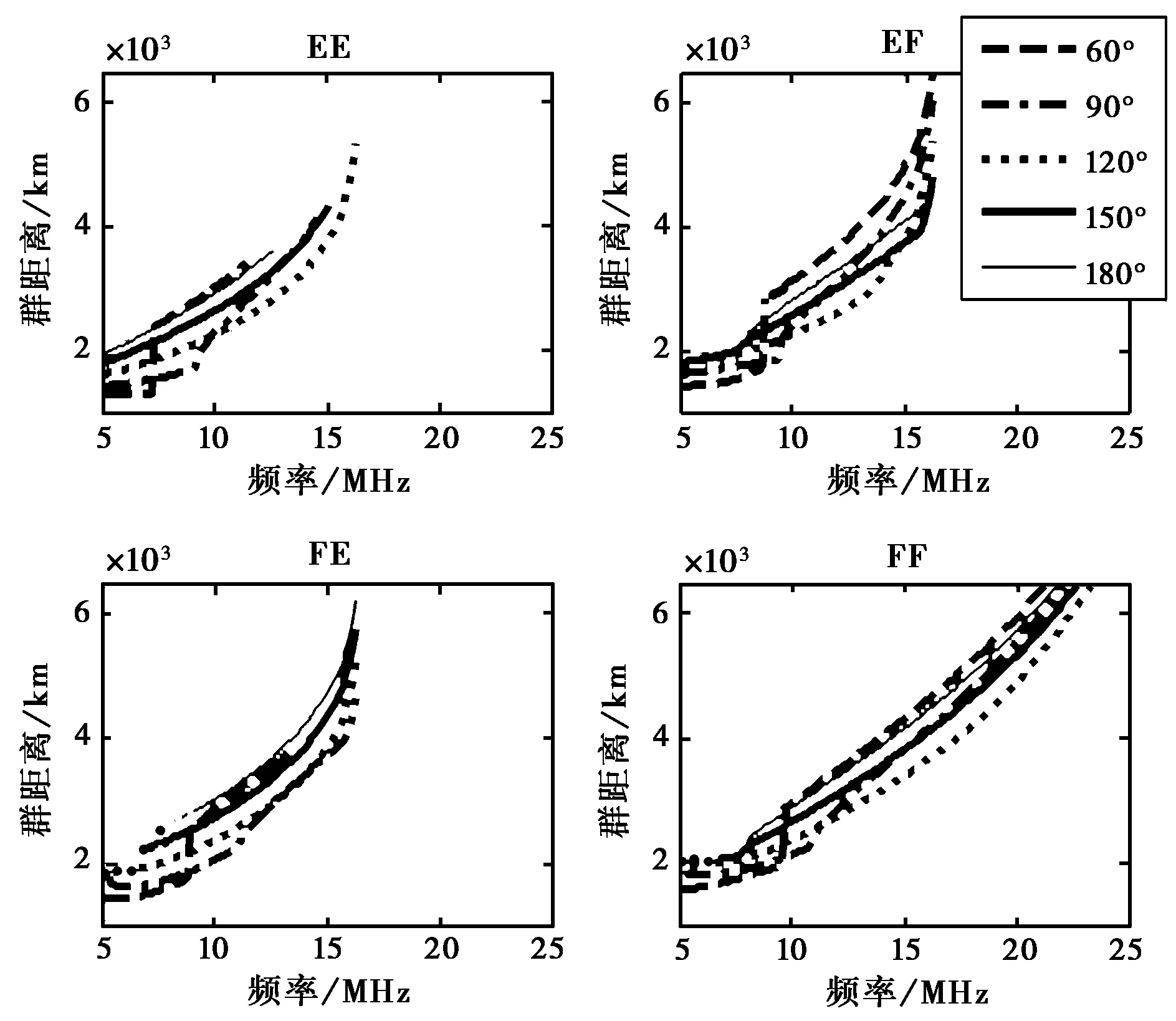
图12 不同波束指向时最小时延线的变化情况

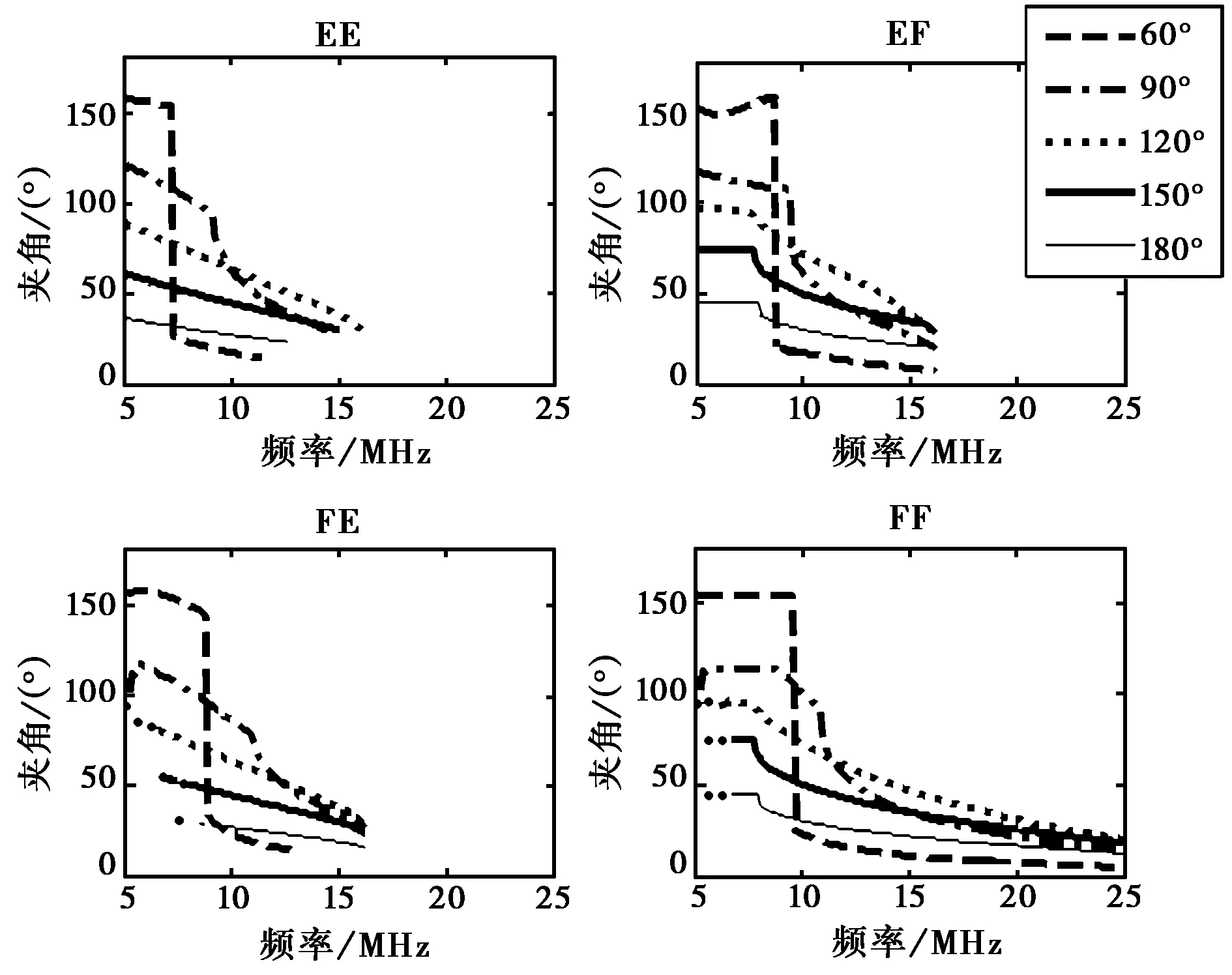
图13 最小时延线上散射单元对应夹角的变化情况

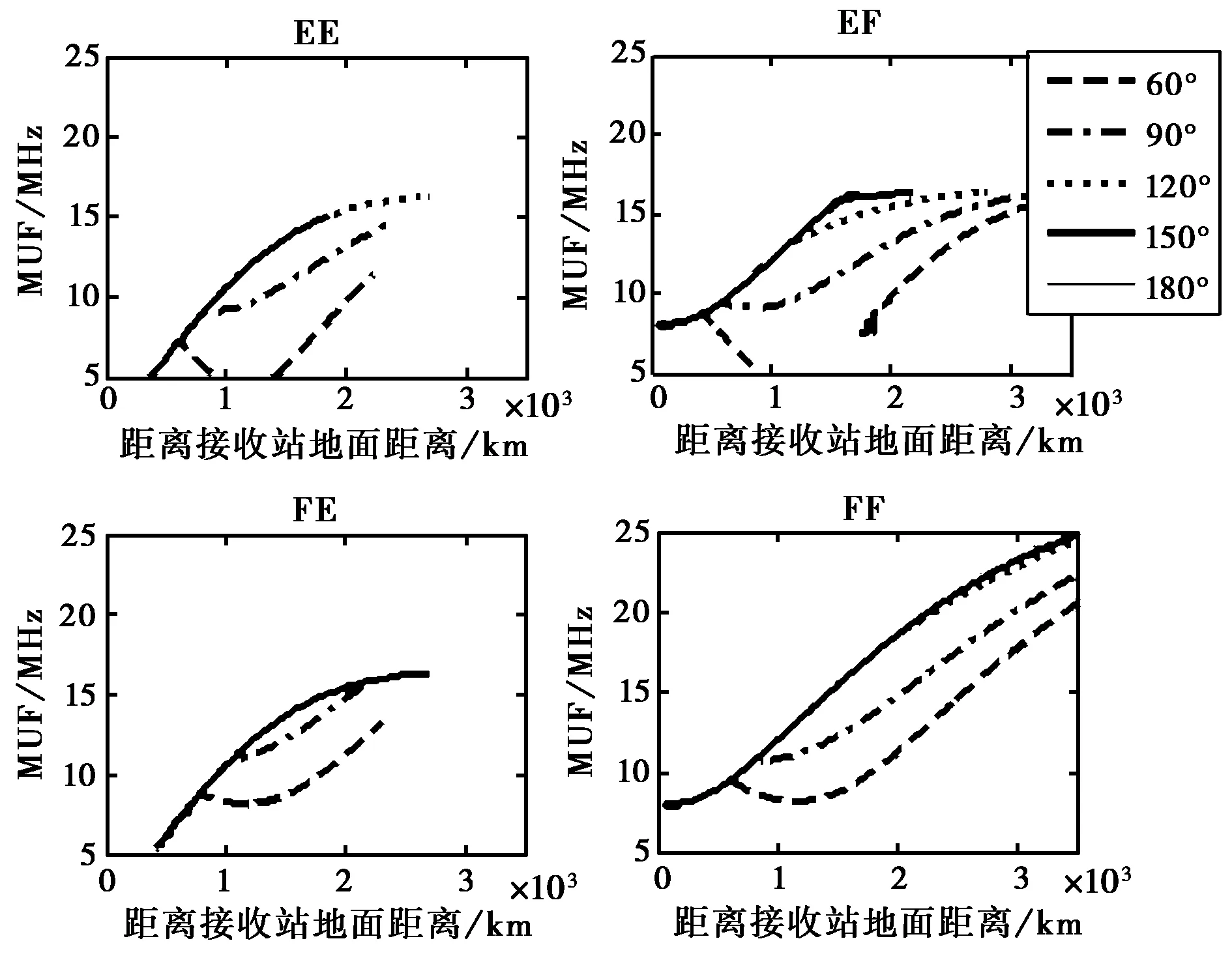
图14 不同波束指向时不同地面距离MUF的变化情况

4 结 论

本文详细推导了侧向散射来波信号的信噪比方程，合成了不同接收波束指向下的侧向散射扫频电离图，给出了最小时延线、不同地面距离MUF等的变化规律.

需要说明的是，本文只给出了两组电离层参数的仿真结果，改变几组电离层参数得到的结果基本一致，但即使这样，最小时延线、不同地面距离MUF等的变化规律的普适性还需要进一步验证. 另外，仿真时，发射天线假设为全向天线，且接收天线未考虑旁瓣的影响，如果和实测结果进行比对，收发天线的方向图务必要考虑到.

[1] 柳 文, 孔庆颜, 陈 跃, 等. 基于IRI模型的垂测电离图自动判读算法研究[J]. 电波科学学报, 2009, 24(2): 218-223.

LIU Wen, KONG Qingyan, CHEN Yue, et al. Method on ionogram autoscaling based on IRI model[J]. Chinese Journal of Radio Science, 2009, 24(2): 218-223. (in Chinese)

[2] 凡俊梅, 焦培南, 吴振森, 等. 电离层不同传播模式信号多普勒频移的实验研究[J]. 电波科学学报, 2008, 23(1): 34-40.

FAN Junmei, JIAO Peinan, WU Zhensen, et al. Experiment research on ionospheric Doppler shift for different propagation [J]. Chinese Journal of Radio Science, 2008, 23(1): 34-40. (in Chinese)

[3] 焦培南, 凡俊梅, 吴海鹏, 等. 高频天波返回散射回波谱实验研究[J]. 电波科学学报, 2004, 19(6): 643-648.

JIAO Peinan, FAN Junmei, WU Haipeng, et al. The experimental research of the Doppler spectrum by HF skywave backscattering[J]. Chinese Journal of Radio Science, 2004, 19(6): 643-648. (in Chinese)

[4] 孙广俊, 齐东玉, 李铁成. 利用返回散射系统监测海洋回波[J]. 电子学报, 2005, 33(7): 1334-1337.

SUN Guangjun, QI Dongyu, LI Tiecheng. Sea echo detection with the system of ionospheric backscatter sounding[J]. Acta Electronica Sinica, 2005, 33(7): 1334-1337. (in Chinese)

[5] 焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007: 278-279.

[6] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008: 362-363.

[7] WEI Na. The simulation research of ionospheric side-scatter ionogram[C]∥ Proceedings of the 10th International Symposium on Antennas, Propagation and EM Theory. Xi’an, October 22-26, 2012:478-481.

[8] 蔚 娜, 柳 文, 李 强, 等.电离层侧向散射探测试验研究[J]. 电子学报, 2012, 40(9): 1710-1714.

WEI Na, LIU Wen, LI Qiang, et al. The experimental research of ionospheric sidescatter sounding[J]. Acta Electronica Sinica, 2012, 40(9): 1710-1714. (in Chinese)

[9] JONES R M. A three dimensional ray-racing computer program[J]. Radio Science, 1968, 3(1): 93-94.