基于改进型三角积分调制的电磁干扰抑制方法

薛开昶 李骄松 林 君 周逢道 刘长胜

(吉林大学仪器科学与电气工程学院，吉林 长春 130061)

引 言

开关电源工作于开关状态，是典型的电磁干扰(Electromagnetic Interference，EMI)源[1]，EMI会通过传导和辐射进行传播．对于以传导形式传播的EMI，主要有两方面影响：一方面通过输入端给电网注入高频谐波，影响电网电能质量；另一方面在输出端向外提供能量的同时也将自身的高频谐波引入到用电设备中，影响用电设备的性能．同时，开关电源会向外围空间辐射EMI，对周围设备和生物造成影响．国际CISPR22标准、美国FCC标准第15部分和中国GB9254标准对电子产品传导和辐射方式下允许的EMI峰值均做出了明确规定．因此，降低开关电源的EMI峰值具有实际意义．

目前，抑制开关电源EMI峰值的一种典型技术是频谱扩散技术，其核心思想为将开关电源中聚集于开关频率及其谐波频率上的能量分布在更多的频率上，使单根频谱能量降低，从而提升电磁兼容(Electromagnetic Compatibility，EMC)效果．文献[2-3]主要论述基于随机脉冲宽度调制(Pulse Width Modulation，PWM)方式的频谱扩散技术，具体包括随机周期PWM、随机脉冲位置PWM和随机开关PWM．在文献[4-5]中，M． Kuisma对频谱扩散技术抑制开关电源EMI峰值的原理进行了综述性分析，通过M． Kuisma的分析可知频谱扩散的关键在于实现频率随机变化的装置和随机信号源的质量．

信号采集领域的三角积分(Sigma-Delta，Σ-Δ)调制[6-9]电路具有输出频率随输入大小变化而变化的特点，是实现频率随机的装置．同时，通信领域的m和逆m序列[10-16]具有与随机噪声相似的性质，是良好的随机源．因此，本文提出一种基于改进型Σ-Δ调制的频谱扩散技术；它利用Σ-Δ调制电路作为实现频率随机的装置，利用m和逆m伪随机序列作为随机信号源．与信号采集领域Σ-Δ调制直接应用于开关电源的方式相比，改进型Σ-Δ调制克服了输出平均频率波动过大，恒定直流输入时输出频率随机度低和恒定采样频率引入固定干扰的不足．

1 开关电源的调制方式

开关电源的控制原理如图1所示，Vg为给定，即参考输入，Vo为功率拓扑电路的输出．Vg与Vo之差为误差信号x(t)，x(t)经过调制电路的处理产生高低电平信号y(t)，y(t)信号经隔离处理后驱动不同的功率电路．

开关电源调制方式主要采用PWM和正弦脉冲宽度调制(Sinusoidal Pulse Width Modulation，SPWM)．但PWM和SPWM开关电源在开关频率及其谐波频率上EMI峰值较高．当调制方式采用Σ-Δ调制时，开关电源产生的EMI峰值将低于PWM和SPWM．Σ-Δ调制被广泛应用于信号采集领域，当将其应用于开关电源时，其理论仍有一些不完善之处．本文将着重对一些与开关电源应用相关的理论和原理进行推导．下文将信号采集领域Σ-Δ调制简称为常规Σ-Δ调制；针对常规Σ-Δ调制存在的不足，提出的新型调制称为改进型Σ-Δ调制．

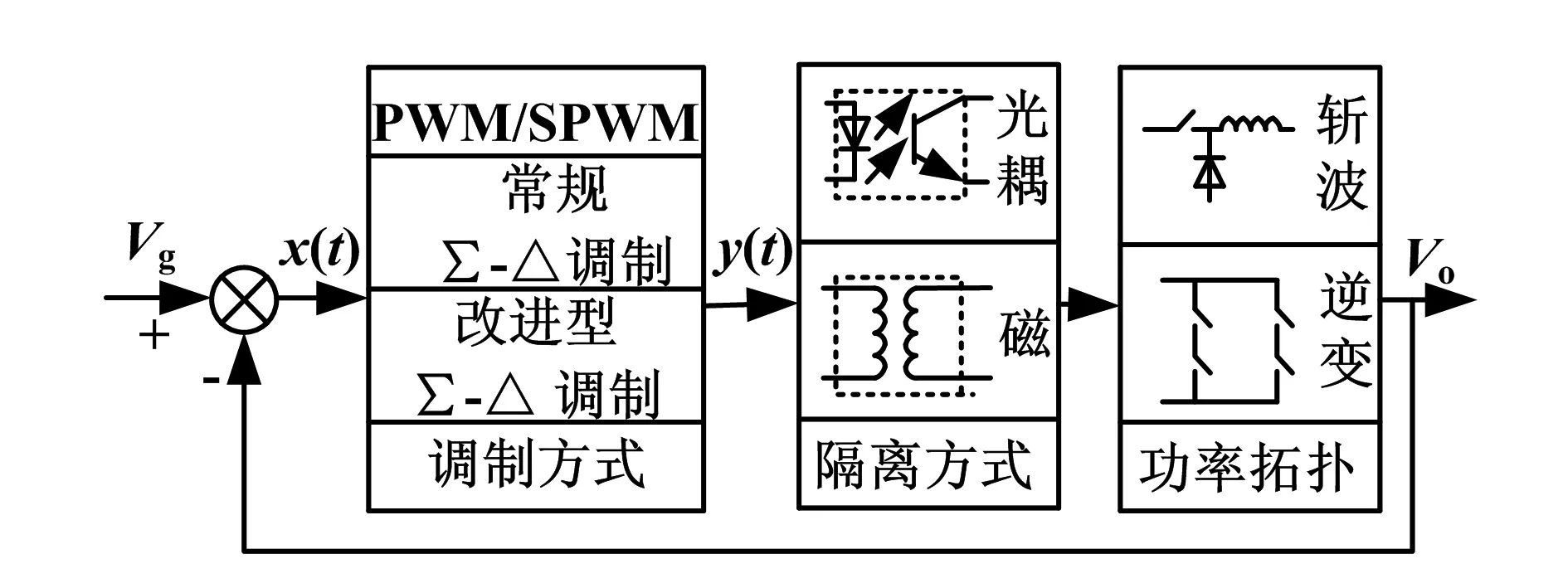
图1 开关电源控制原理

2 常规Σ-Δ调制的原理

2.1 常规Σ-Δ调制的硬件原理

常规Σ-Δ调制的原理[7]如图2所示，输入信号x(t)为图1中误差信号；对于Buck、Boost、Buck-Boost等斩波电路，x(t)可以认为是一个直流，可称这种情况为直流模式；对于半桥、全桥等正弦波输出逆变器，x(t)可以认为是一个正弦波，可称这种情况为交流模式．y(t)为x(t)对应的输出信号，y(t)为一串按采样时钟频率fs切换的数字信号，经适当处理后可以用于驱动功率开关，y(t)的高低电平分别为Vb和-Vb．

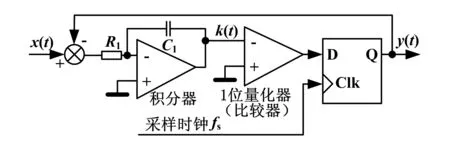
图2 常规Σ-Δ调制的硬件原理

2.2 输入信号对输出频率的影响

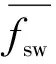
(1)

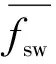
(2)

2.3 常规Σ-Δ调制抑制EMI的原理

由式(1)和式(2)可知当输入x(t)存在波动时，输出y(t)的平均频率也会随之变化．

由图2可知，即使在输入保持恒定的情况下，由于量化器输出在积分器输出过零时发生变化，y(t)在采样时钟上升沿发生变化，两者之间存在一定时差，相互之间是异步的，故y(t)也具有一定的频率随机度．

因此，Σ-Δ调制具有变频功能，能将常规PWM和SPWM中集中于开关频率及其谐波上的能量分布在更多的频率成份上，使各个频率点上的能量降低，达到抑制开关电源EMI的作用．

2.4 常规Σ-Δ调制的不足

1) 输出平均频率波动过大．由式(1)可知在直流模式下，调制系数|Va/Vb| = 0～0.9时，输出y(t)的平均频率将在(1/2～1/20)fs的范围内变化；由式(2)可知在交流模式下，调制系数|Va1/Vb| = 0～0.9时，输出y(t)的平均频率将在(1/2～1/4.68)fs的范围内变化，且在正弦波正负峰值处，瞬时频率极低．输出频率变化较大，使得开关电源中的电感器设计和开关管的散热设计变得困难．

2) 恒定直流输入时输出频率随机度低．对于直流模式，当输入x(t)波动很小或者基本没有波动时，输出y(t)各个脉冲周期相差不大，随机程度不高，所含的频率成份也较少，从而EMC效果不佳．

3) 恒定采样频率引入固定干扰．由于输出y(t)切换是在采样时钟上升沿发生，故不可避免地会引入采样时钟频率及其谐波频率的固定干扰，从而降低Σ-Δ调制的EMC效果．

3 改进型Σ-Δ调制的原理

常规Σ-Δ调制的不足使其在开关电源中难于使用．对常规Σ-Δ调制进行改进，可以减轻或消除上述不足．改进型Σ-Δ调制原理如图3所示．

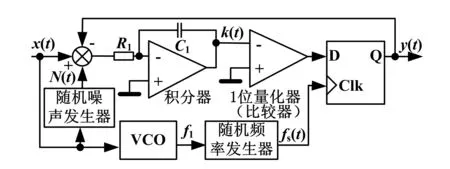
图3 改进型Σ-Δ调制原理

根据式(1)，有

(3)

根据式(3)，在输入恒定时，输出平均频率也是定值，然而频率扩散需要输出频率在小范围内有一定的波动．因此，可以在输入端加一随机噪声，使输出频率有一定变化，设随机噪声N(t)的峰峰值为ΔVa．根据式(1)，有：

(4)

(5)

式(4)和式(5)中：Δ表示变化量，相当于微分算符．

故ΔVa可以用式(5)求取．图3中的随机噪声发生器根据式(5)产生峰峰值为ΔVa的噪声信号N(t)．这样即可克服常规Σ-Δ调制恒定直流输入时输出频率随机度低的不足．

为了克服常规Σ-Δ调制中恒定采样频率引入固定干扰的不足．可用图3中的随机频率发生器，使采样时钟频率在一定范围内波动．

4 m和逆m序列随机发生器

4.1 m及逆m伪随机序列产生原理

图4为m和逆m伪随机序列产生示意图[10]，把n个D触发器从左往右依次按1至n排列，依次串联构成移位寄存器，当在驱动时钟Clk的上升沿到来时，后一个D触发器将会存储前一个D触发器上的逻辑．对于第一个D触发器，它的输入由特征多项式决定，特征多项式为

f(x1,x2,…,xn)=anxn+…+a2x2+a1x1+1.

(6)

式中: (a1，a2，…，an)∈{0，1}；xi为第i个D触发器的输出，当ai为1时，第i个D触发器的输出将会送到1位模2加法器(即1位二进制加法器，可由异或运算实现)求和，最终求和结果将作为第一个D触发器的输入．第n个D触发器的输出xn即为m伪随机序列信号．对m伪随机序列隔位取反即为逆m伪随机序列(图中用L表示)，通过Clk二分频后与m伪随机序列相异或的方式实现隔位取反．初始化时，将Reset置1，使各个D触发器输出全为1．

图4 m和逆m伪随机的产生

当n为3～7时，m序列的特征多项式系数如表1[11]所示．特征多项式系数按an为最高位，a1为最低位排列，以十六进制形式表示．k表示特征多项式系数的个数．对于n位D触发器构成的移位寄存器，一个m伪随机序列周期的Clk时钟数为

N=2n-1.

(7)

表1 m伪随机序列特征多项式系数

n= 4，特征多项式系数为C和9时，x4x3x2x1的变化规律如图5所示．由图5可以看出1～F是等概率出现的，同时在不同的特征多项式系数下循环的规律也不同．因此可以用m序列产生随机数xn…x2x1，用于实现图3改进型Σ-Δ调制中的随机频率发生器．

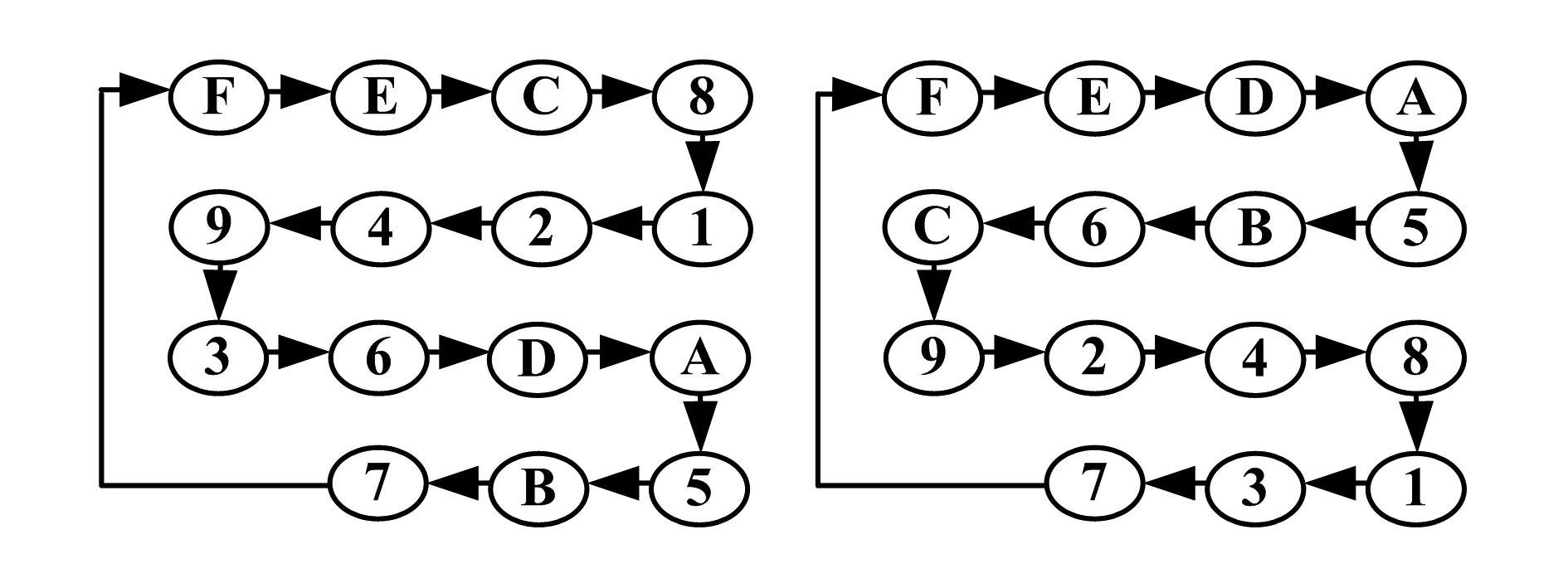
(a) 系数为C (b) 系数为9图5 n = 4时m序列产生的随机数

n= 4，特征多项式系数为C时，逆m伪随机序列的波形如图6所示．图中深色线表示一个周期．因为如图6所示的逆m序列0和1等概率出现，有与白噪声类似的自相关函数，具有与白噪声类似的一些特性，同时，真正的白噪声又不易产生，故可以用逆m序列替代白噪声．因此，可以用逆m伪随机序列实现图3改进型Σ-Δ调制中的随机噪声发生器．

图6 n = 4时逆m伪随机序列波形

4.2 随机频率发生器设计

当m伪随机序列的D触发器个数为n，有k个特征多项式系数时．用Nij(i= 1，2，…，k；j= 1，2，…，N)表示第i个特征多项式系数下生成的第j个随机数xn…x2x1的值．Nij的平均值为

(8)

式中N可由式(7)求取．

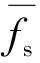
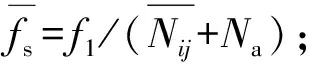
(9)

(10)

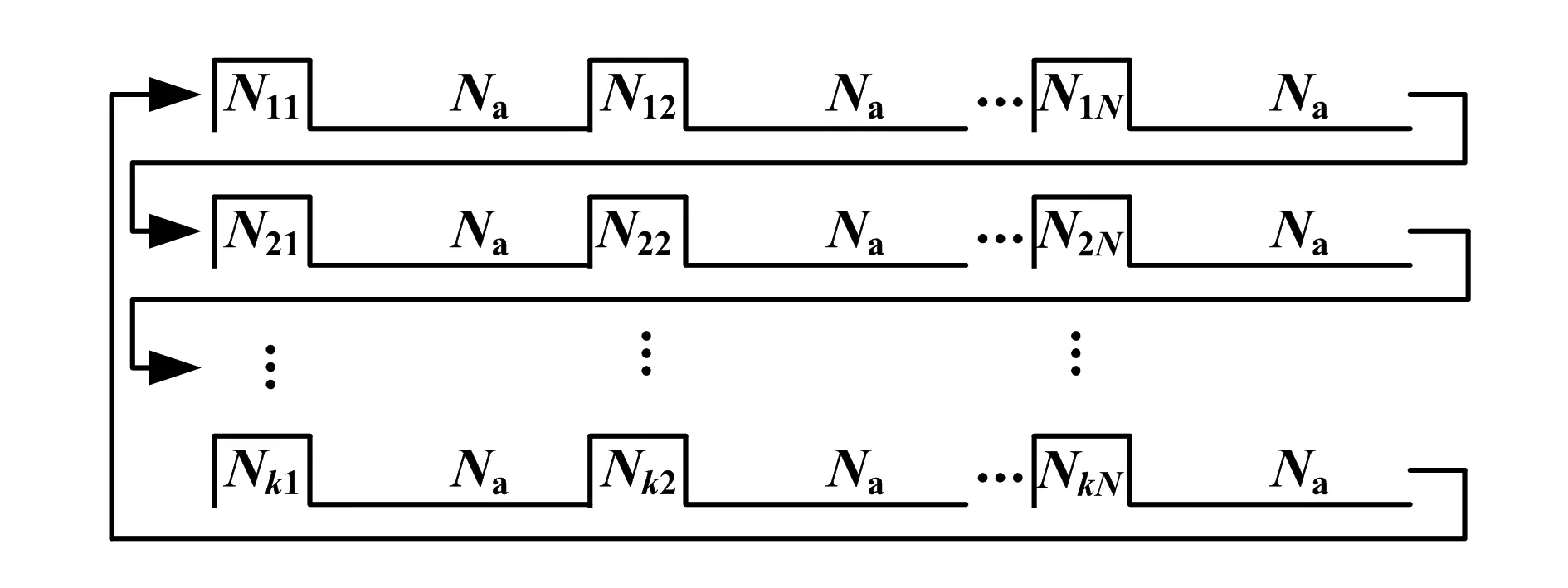
图7 随机频率发生器输出逻辑

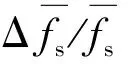
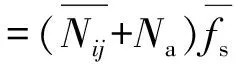
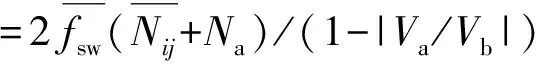
(11)

式(11)即为图3中VCO输入与输出频率的对应关系．根据上述分析可在现场可编程门阵列(Field Programmable Gate Array，FPGA)下实现随机频率发生器．

4.3 随机噪声发生器设计

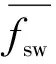
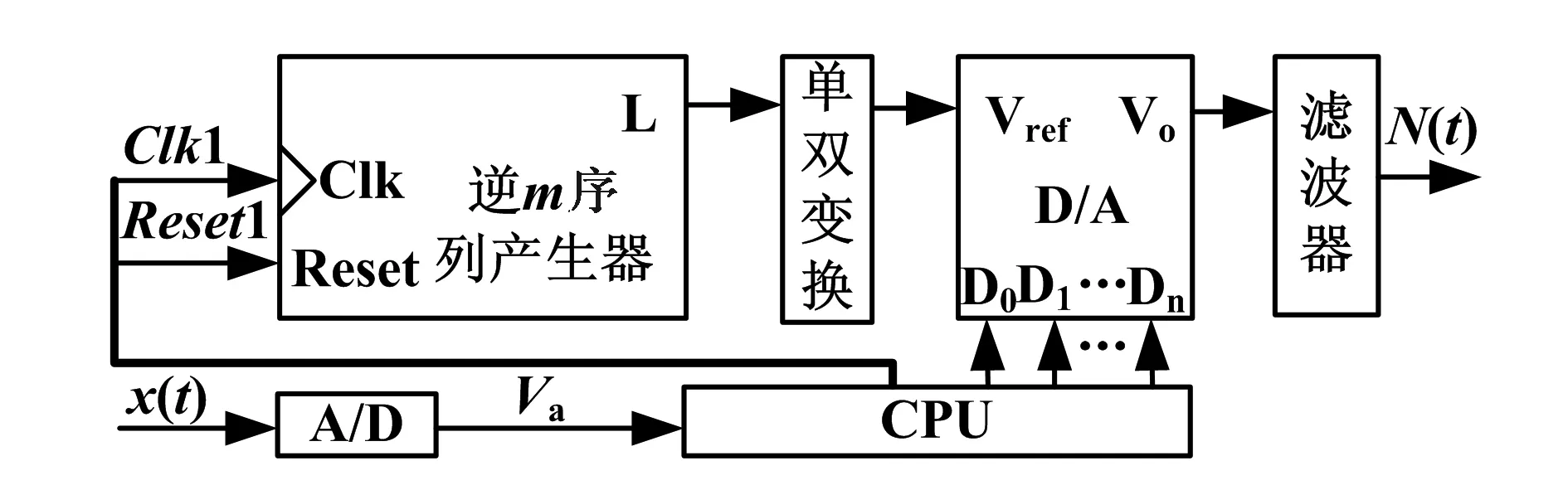
图8 随机噪声发生器原理

5 实验测试结果

分别按图9、图2和图3构建常规PWM、常规Σ-Δ调制和改进型Σ-Δ调制电路．图9中双向稳压管Vz的电压为±5.8 V，改进型Σ-Δ调制中的随机噪声发生器和随机频率发生器按第4节所述方法实现．三个电路中输入x(t)为2.32 V直流，输出驱动y(t)的高电平为5.8 V，低电平为-5.8 V．实测波形图和频谱图采用TDS2012B示波器及自带快速傅里叶变换(Fast Fourier Transform，FFT)功能获取．

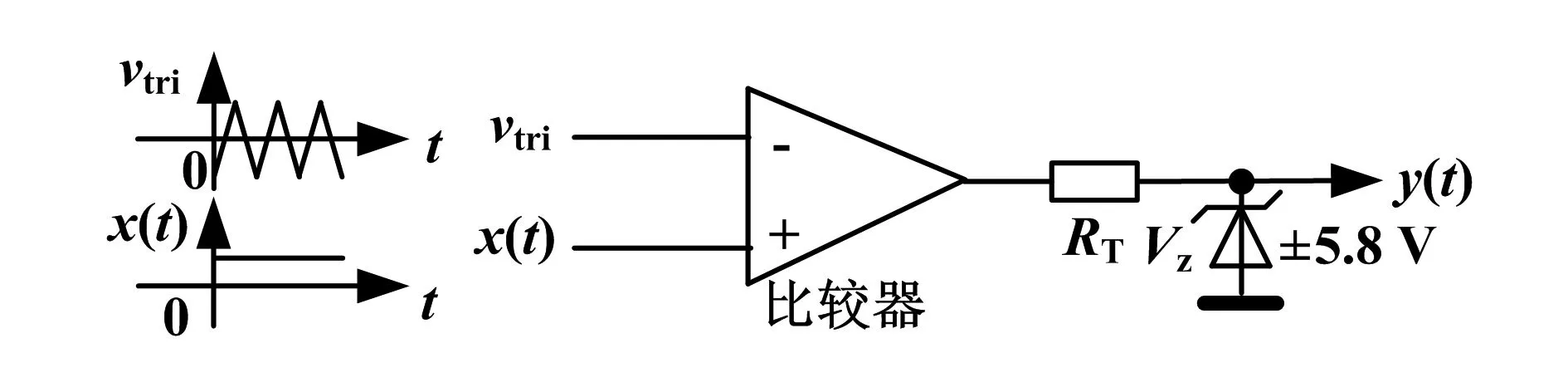
图9 常规PWM测试电路

在图9所示电路中，当输入x(t)与正负对称20 kHz、11.6 V峰峰值的三角波vtri比较，可得到常规PWM输出驱动y(t)；y(t)的实测波形y1和频谱Y1如图10所示．在图2所示常规Σ-Δ调制中，采样频率fs为66.7 kHz时，可得平均频率为20 kHz的驱动波形；y(t)的实测波形y2和频谱Y2如图11所示．在图3所示改进型Σ-Δ调制中，通过本文所述方法设置输出平均频率为20 kHz，随机噪声发生器采用n= 4，时钟频率为2 048 Hz的逆m序列，随机频率发生器采用n= 4的m序列；y(t)的实测波形y3和频谱Y3如图12所示．

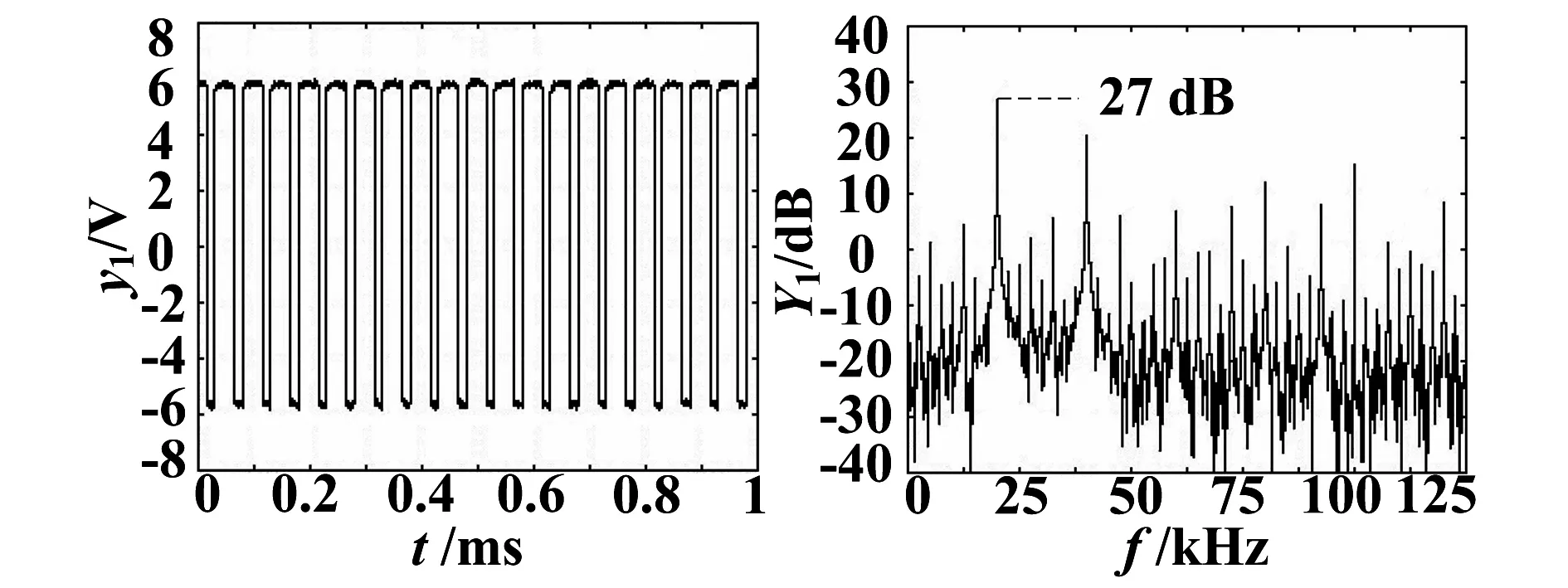
(a) 波形图 (b) 频谱图图10 常规PWM中y(t)的波形和频谱

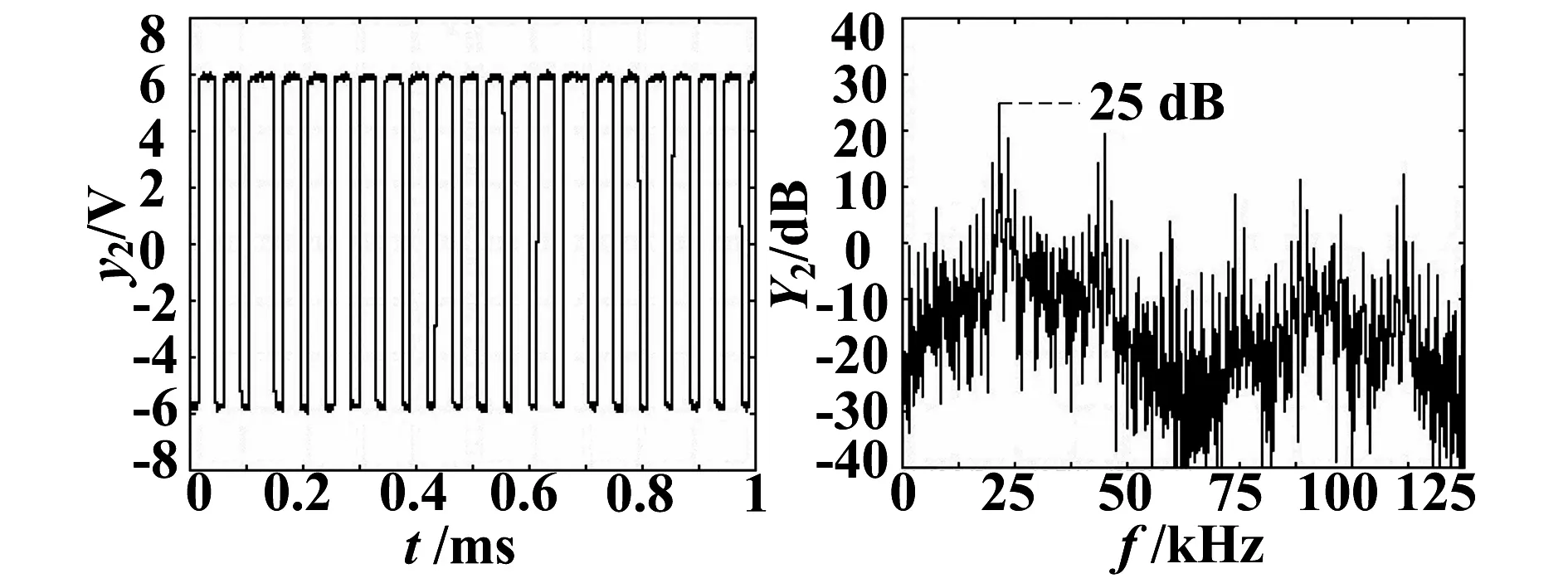
(a) 波形图 (b) 频谱图图11 常规Σ-Δ中y(t)的波形和频谱

(a) 波形图 (b) 频谱图图12 改进型Σ-Δ中y(t)的波形和频谱

对比图10～12可以看出常规Σ-Δ调制与PWM相比有一定的EMI峰值抑制效果，但是效果不佳，仅有2 dB的改善；改进型Σ-Δ调制与PWM相比却有12 dB的改善．实验结果表明本文提出的改进型Σ-Δ调制在抑制开关电源EMI峰值方面效果明显．

6 结 论

常规Σ-Δ调制直接应用于开关电源存在输出平均频率波动过大，恒定直流输入时输出频率随机度低和恒定采样频率引入固定干扰的不足．改进型Σ-Δ调制通过使采样频率跟踪输入大小，添加随机噪声和使采样频率随机化的方法克服了常规Σ-Δ调制的不足．实测结果表明，改进型Σ-Δ调制的EMI峰值低于常规Σ-Δ调制10 dB，EMI峰值抑制效果优于常规PWM和常规Σ-Δ调制．

[1] 路宏敏，梁昌洪，李晓辉，等．开关电源散热器的辐射发射[J]．电波科学学报，2005，20(2)：241-246．

LU Hongmin，LIANG Changhong，LI Xiaohui，et al．Radiated emissions from heatsinks in SMPS[J]．Chinese Journal of Radio Science，2005，20(2)：241-246．(in Chinese)

[2]LIN B R．High power factor AC/DC/AC converter with random PWM[J]．IEEE Transactions on Aerospace and Electronic Systems，1999，35(3)：935-944．

[3] GUO Haiyan，WU Haizhou，ZHANG Bo，et al．A novel spread-spectrum clock generator for suppressing conducted EMI in switching power supply[J]．Microelectronics Journal，2010，41(2/3)：93-98．

[4] KUISMA M，RAUMA K，SILVENTOINEN P．Using switching function in preliminary EMI-analysis of a switching power supply[C]// IEEE Annual Power Electronics Specialists Conference．Recife，2005：994-998．

[5] KUISMA M．Variable frequency switching in power supply EMI-control：an overview[J]．IEEE Aerospace and Electronic Systems Magazine，2003，18(12)：18-22．

[6]PARAMESH J，JOUANNE A．Use of sigma-delta modulation to control EMI from switch-mode power supplies[J]．IEEE Transactions on Industrial Electronics，2001，48(1)：111-117．

[7] HSIEH G C，CHEN H L．Analytic modelling and realisation for sigma-delta-modulated power amplifier[J]．IET Power Electron，2009，2(5)：496-507．

[8] BAE C H，RYU J H，LEE K W．Suppression of harmonic spikes in switching converter output using dithered sigma-delta modulation[J]．IEEE Transactions on Industrial Applications，2002，38(1)：159-166．

[9] TORMO A G，POVEDA A，ALARCON E，et al．Design-oriented characterisation of adaptive asynchronous ΣΔ modulation switching power amplifiers for bandlimited signals[C]// IEEE International Symposium on Circuits and Systems．Taipei，2009：2882-2885．

[10] 樊昌信，张甫翊，徐炳袢，等．通信原理[M]．5版．北京：国防工业出版社，2006：326-347．

[11] 田小平，吴明捷．利用窗口法寻找产生伪随机码的本原多项式[J]．北京石油化工学院学报，2003，11(2)：1-4．

TIAN Xiaoping，WU Mingjie．Using window method to look for primitive polynomial which generate pseudo noise code[J]．Journal of Beijing Insitute of Petro-chemical Technology，2003，11(2)：1-4．(in Chinese)

[12] ZOIROS K E，DAS M K，GAYEN D K，et al．All-optical pseudorandom binary sequence generator with TOAD-based D flip-flops[J]．Optics Communications，2011，284(19)：4297-4306．

[13] ROINILA T，VILKKO M，SUNTIO T．Frequency-response measurement of switched-mode power supplies in the presence of nonlinear distortions[J]．IEEE Transactions on Power Electronic，2010，25(8)：2179-2187．

[14] LIM Y C，WI S O，KIM J N，et al．A pseudorandom carrier modulation scheme[J]．IEEE Transactions on Power Electronic，2010，25(4)：797-805．

[15] 陈 罡，赵正予，杨国斌．近完美序列与m序列的分析和比较[J]．电波科学学报，2008，23(1)：68-73．

CHEN Gang，ZHAO Zhengyu，YANG Guobin．Analysis and comparison of almost perfect sequences andmsequences[J]．Chinese Journal of Radio Science，2008，23(1)：68-73．(in Chinese)

[16] 陶海红，廖桂生，王 伶．基于混合遗传算法的m序列波形优化设计[J]．电波科学学报，2004，19(3)：253-257．

TAO Haihong，LIAO Guisheng，WANG Ling．Novelm-sequences waveform design using the hybrid genetic algorithm[J]．Chinese Journal of Radio Science，2004，19(3)：253-257．(in Chinese)