混合智能优化频率指配算法
王 凡 董 俊 卢冬鸣 姬生云
(1.电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003;2.中国电波传播研究所,山东 青岛 266107)
引 言
作为电磁频谱管理的核心技术之一,频率指配(Frequency Assignment)是指对无线电设备指定具体使用频率,以确保其可以在复杂的电磁环境中有效、兼容地工作,是实行频谱管理的最终体现[1].频率指配问题在本质上讲属于组合优化问题,是一个非确定多项式完全(Nondeterministic Polynomial Complete, NPC)问题[2],算法运算时间会随问题规模增大成指数级“爆炸性”递增.在早期,由于用频设备数量较少且工作方式较为简单,故解决这种小规模网络的频率指配问题并不十分困难,采用传统的人工分段划分、穷取法等即可解决.随着无线通信技术的飞速发展,网络规模的不断扩大,各种无线电业务对频谱资源的需求迅速增长,频率指配问题的难点已经转化为如何在有限的时间内为大规模的复杂网系找到高质量的解,传统方法已经难以有效解决.
智能优化算法的提出为上述问题提供了解决方案.智能优化算法,多源于人工智能领域[3-10],其实质是一种搜索规则或过程,它基于某种思想或机制,也可以是多种思想的结合,主要思路是采取确定或概率的方法,控制搜索空间的指数膨胀,在合理的时间内给出最优解或次优解.由于频率指配问题的困难性,目前国内外学者研究了大量利用智能优化算法解决频率指配问题的技术[11-14],包括:禁忌搜索(Tabu Search,TS)算法、模拟退火(Simulated Annealing,SA)算法、遗传算法(Genetic Algorithm,GA)、蚁群算法(Ant Colony Algorithms,ACO)等.由于各种智能优化算法各有优缺点,根据各算法的特点,将两种乃至两种以上的智能优化算法相结合的混合算法通常具有更佳的优化效果[15].
本文提出了一种结合禁忌搜索和模拟退火算法优点的混合智能优化算法来解决频率指配问题,仿真结果表明,该方法可有效提升搜索效率和精度,鲁棒性强,优于两种算法单独应用的情况.
1 算法原理介绍及设计
1.1 模拟退火和禁忌搜索算法原理介绍
模拟退火算法的出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性,在某一初温下,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即能够跳出局部最优解并最终趋于全局最优解,具有解质量高、鲁棒性强、通用易实现等优点[12].
禁忌搜索算法模仿人类的记忆功能,通过对一些局部最优解的禁忌达到接纳一部分较差解,从而跳出局部搜索;通过引入一个灵活的存储结构和相应的禁忌准则来避免迂回搜索;同时赦免禁忌区域中的一些优良状态,进而保证搜索的多样性,从而达到全局最优[11].
1.2 混合智能优化频率指配算法设计
模拟退火算法在局部极小解处有机会跳出并最终趋于全局最优的根本原因是通过概率判断来接受新状态,这在理论上也已得到严格证明,即当初温充分高、降温足够慢、各温度下抽样次数足够多、最终温度趋于零时,算法最终以概率1收敛到全局最优解[16].一般来说,模拟退火算法为寻求最优解,通常要求较高的初温、较慢的降温速度、较低的终止温度以及热平衡时间足够长(即各温度下足够多次的抽样),因而模拟退火算法的特点是全局优化能力强,但往往优化过程较长.且由于概率突跳特性,模拟退火算法会接受性能较差的解,所以其最终解可能比运算过程中遇到的最好解性能差.考虑禁忌搜索算法具有记忆功能的优点,且局部优化能力强,搜索速度快的特点,故将模拟退火算法和禁忌搜索算法的优点相结合,提出一种混合智能优化频率指配算法(SA-TS),主体结构采用模拟退火算法,为避免搜索过程中由于执行概率接受环节而遗失当前遇到的最优解,增加禁忌搜索算法的记忆功能,通过增加存储环节,在算法搜索过程中保留中间最优解,并即时更新.
下面阐述混合智能优化算法应用到具体的频率指配问题中各要素的设计:
1) 可用频率
设当前指配中可用的频率资源为:F=(f1,f2,…,fNF),可用频率数为NF.
2) 解
用S=
3) 代价函数
在频率指配过程中,代价函数(即目标优化函数)cost(S)可以包含以下几项:违背约束惩罚值evio;(即不满足约束关系的指配频率的代价值);指配解的最高频率flarge和最低频率fsmall之差;所用不同频率的数目eorder.代价函数值在算法运行过程中随着迭代步数的变化而变化,算法的最终目标是使cost(S)达到最小,即min(cost(S)).
目标优化函数可以用下式表示
cost(S)=μ1evio+μ2(flarge-fsmall)+μ3eorder.
(1)
目标优化函数可以根据用户需求选取其中一项或几项之和.
4) 邻集
给定一个当前解S0,它的邻集V的解定义如下:给定一个新解SN,SN与S0相邻当且仅当
(2)
此邻集中的解表示当前解有且仅有一条链路改变频率,故当前解S0共有N(NF-1)个邻域解.这样构造邻域结构能够提高效率,每次产生新解时只更新一个链路的频率,以免一次更新多个链路的频率, 使得在某些链路找到最优频率的同时, 其它一些已经处在最优频率的链路又更换了频率, 很难使所有链路同时找到最优频率.
5) 新解产生方法
为了遍历所有邻域解,用一个随机搜索过程产生当前解S=
a) 随机选择一条链路v,(v∈[1,2,…,N]);
b) 随机选择一个新频率fi,(i∈[1,2,…,NF]);
c) 将新频率fi指配给链路v,且不同于链路v的旧频率.
6) 新解接受准则
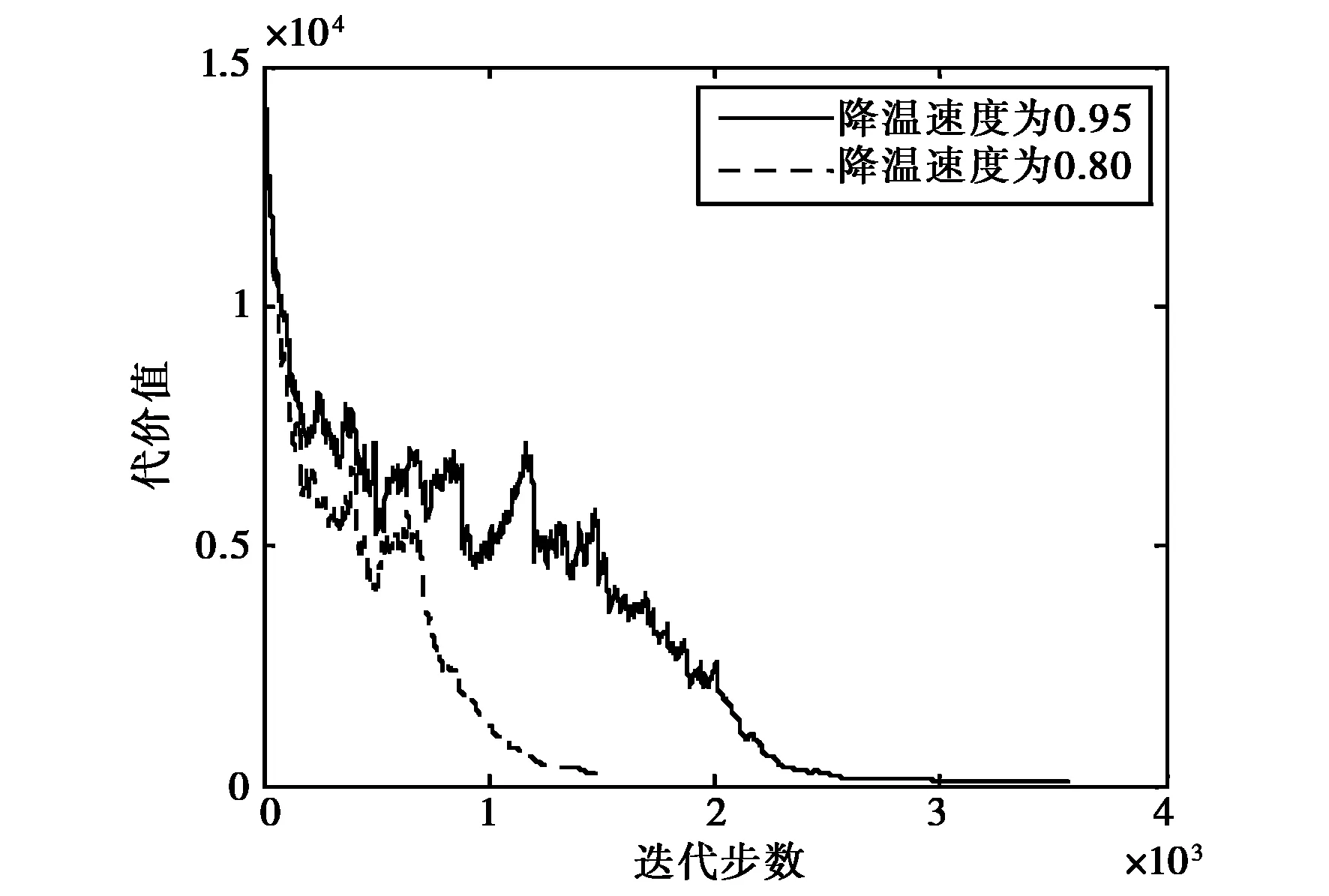
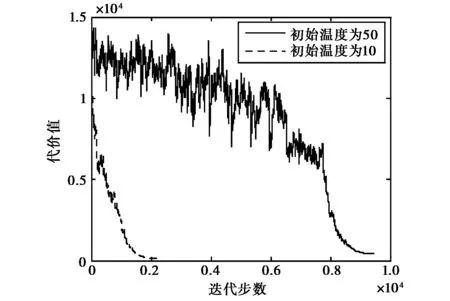
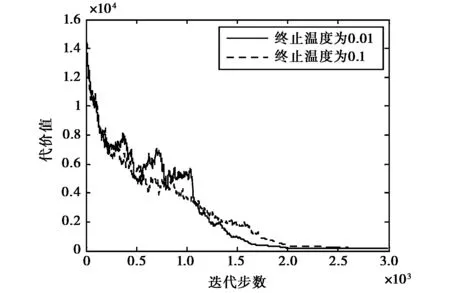
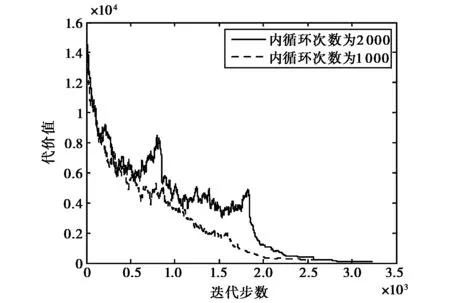
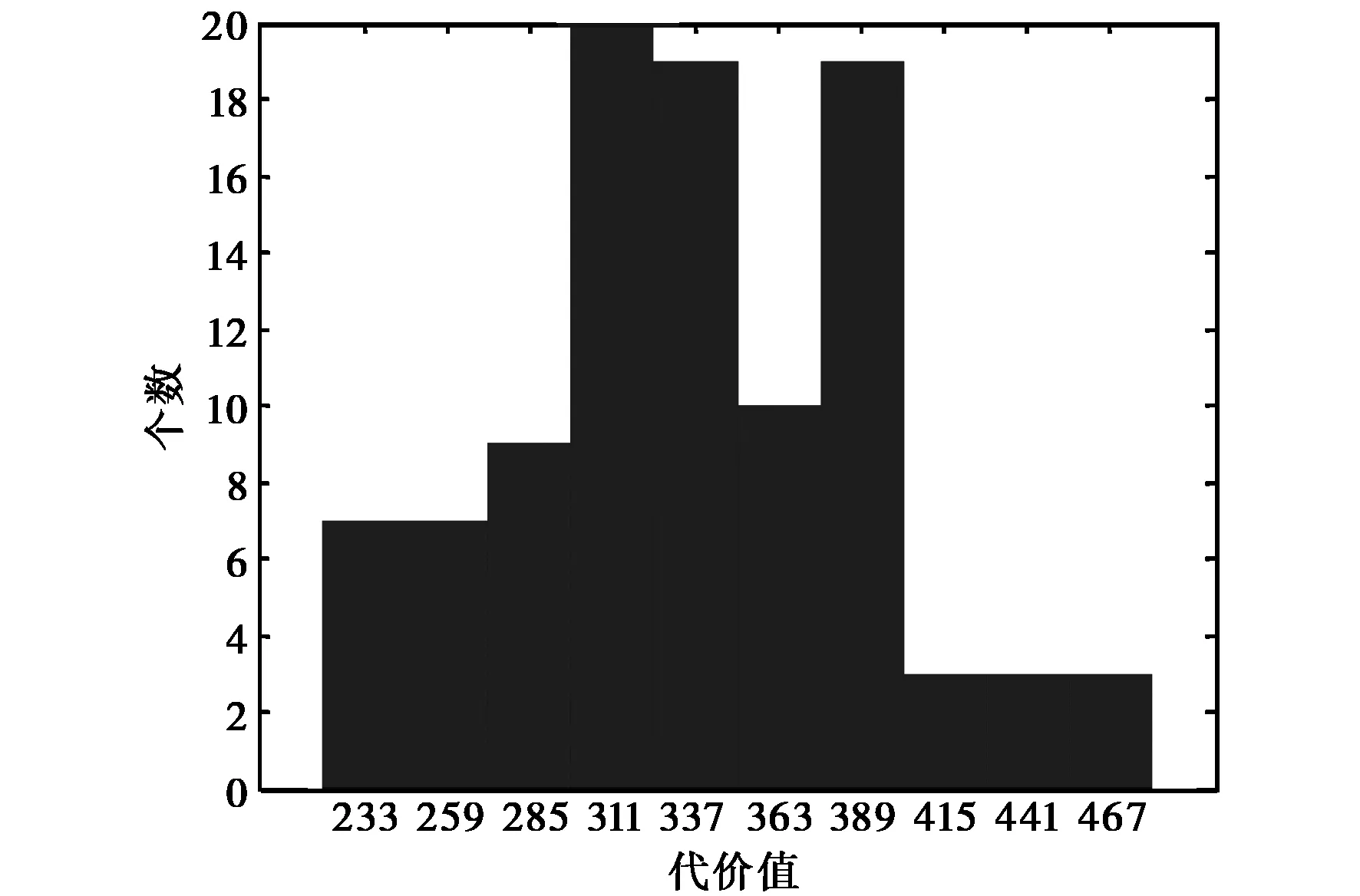
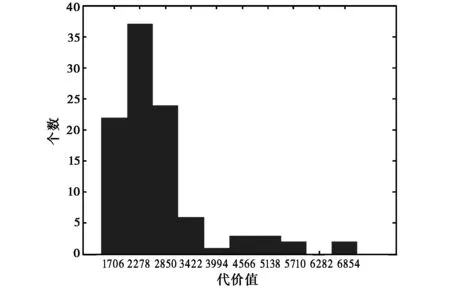
对于一个新解,根据Metropolis抽样准则[16]来判断是否接受新解,即在每一次迭代过程中,从当前解S0的邻集中选取一个SN,若cost(SN) min{1,exp[-[cost(SN)-cost(S0)]/t(k)]} ≥Rand[0,1], (3) 其中: Rand[0,1]为0到1之间的随机变量;t(k)表示退火函数. 7) 退火过程 a) 温度变化周期:每M(即内循环次数)次迭代之后使温度下降; b) 温度下降策略及退火速度设置. 模拟退火算法的全局搜索性能也与退火速度密切相关.一般来说,同一温度下的“充分”搜索(退火)是相当必要的,但这需要计算时间.实际应用中,要针对具体问题的性质和特征设置合理的退火平衡条件,本算法使用的退火函数为 t(k+1)=α·t(k),0<α<1, (4) 其中,α表示降温速度. 8) 终止准则 所设计的终止准则由以下两个元素组成,当温度降低到低于终止温度tm时且当搜索到的最优解连续若干次循环均保持不变时,算法停止运行. a) 设计终止温度的闭值; b) 算法搜索到的最优值连续若干次循环保持不变. 混合智能优化频率指配算法流程如图1所示. 图1 混合智能优化频率指配算法流程图 对于智能优化算法来说,参数是影响算法性能的重要因素,下面仿真分析所设计的混合智能优化频率指配算法中各参数变化对算法性能的影响.其中:α为降温速度;M为内循环次数;t0为初始温度;tm为终止温度. 1) 降温速度对算法的影响 首先,分析降温速度对算法运行时间和解的质量的影响,仿真参数为:链路条数为100,可用频率个数为40,约束矩阵复杂度为0.3(即30%的被指配对象间存在频率间隔约束),初始温度为10,终止温度为0.1,内循环次数为1 000,图2给出了降温速度α=0.8和α=0.95时,SA-TS混合算法频率指配过程代价值随迭代步数的变化曲线图. 图2 不同降温速度代价值变化曲线图 由仿真结果可知,从相同的初始解(代价值为13 820)开始优化,当降温速度分别为α=0.8和α=0.95时,得到的最优解的代价值分别为120、60,在相同硬件配置条件下所花费的时间分别为20.080 s、90.453 s.由此可知,降温速度变慢,可以改善解的质量,但相应会较大程度增加算法的运算时间,在实际应用中,应根据具体情况的要求权衡运行时间和解的质量设置降温速度. 2) 初始温度对算法的影响 下面分析初始温度对算法运行时间和解的质量的影响,仿真参数为:链路条数为100,可用频率个数为40,约束矩阵复杂度为0.3,降温速度为0.9,终止温度为0.1,内循环次数为1 000,图3给出了初始温度t0=50和t0=10时,SA-TS混合算法频率指配过程代价值随迭代步数的变化曲线图. 图3 不同初温代价值变化曲线图 由仿真结果可知,从相同的初始解(代价值为13 820)开始优化,当初始温度t0=50和t0=10时,得到的最优解的代价值分别为320、80,在相同硬件配置条件下所花费的时间分别为44.627 s、189.255 s.由图3可知,当初始温度较高t0=50时,代价下降的趋势比较缓慢,当初始温度较低t0=10时,代价以较快的速度下降,因而可知,代价降到同一个水平值,初温高时耗时远远大于初温低的耗时.由此可见初始温度会影响代价的下降速度,初始温度较高时,运行时间较长,但解的质量并未得到相应的改善,故算法不需设置过高的初始温度. 3) 终止温度对算法的影响 下面分析终止温度对算法运行时间和解的质量的影响,仿真参数为:链路条数为100,可用频率个数为40,约束矩阵复杂度为0.3,降温速度为0.9,初始温度为10,内循环次数为1 000,图4给出了终止温度tm=0.01和tm=0.1时,SA-TS混合算法频率指配过程代价值随迭代步数的变化. 图4 不同终止温度代价值变化曲线图 由仿真结果可知,从相同的初始解(代价值为13 820)开始优化,当终止温度tm分别为0.01和0.1时,得到的最优解的代价值分别为220、140,所花费的时间分别为48.484 s、70.505 s,由此可知,降低终止温度可以得到更好的解,但相应地会增加算法的运行时间,在实际应用中,应根据具体情况的要求权衡运行时间和解的质量设置终止温度. 4) 内循环次数对算法的影响 下面分析内循环次数对算法运行时间和解的质量的影响,仿真参数为:链路条数为100,可用频率个数为40,约束矩阵复杂度为0.3,初始温度为10,降温速度为0.9,终止温度为0.1,图5给出了内循环次数M=2 000和M= 1 000情况下SA-TS混合算法频率指配过程代价值随迭代步数的变化曲线图. 图5 不同内循环次数时代价值变化曲线图 由图5可知,当内循环次数M分别为2 000、 1 000时,得到的最优解的代价值分别为160、100,所花费的时间分别为48.484 s、95.538 s,由此可知增大内循环次数可以得到更好的解,但改善不明显,所花费的时间却成倍增加,在实际应用中,应根据具体情况的要求权衡运行时间和解的质量设置内循环次数. 根据上述内容可以得到混合算法参数设置的基本规律及影响效果,在实际应用中,应根据实际问题的规模、特征等来设置算法参数. 首先,对模拟退火(SA)、禁忌搜索(TS)、混合智能优化(SA-TS)三种频率指配算法的搜索效率和精度进行分析,图6为SA、TS和SA-TS算法的代价变化曲线. 图6 代价(干扰)变化曲线对比图 仿真参数为:链路条数为100,可用频率个数为40,约束矩阵复杂度为0.3,SA和SA-TS算法的初始温度为10,降温速度为0.9,终止温度为0.1,内循环次数为1 000,TS算法的禁忌长度为20.由仿真结果可知,SA、TS和SA-TS算法的最优解的代价值分别为100、1 580、110,运行时间分别为91.123 s、46.798 s、47.629 s.因此可知,在相同的初始解前提下,与SA算法相比,SA-TS算法可在远小于SA算法的搜索时间找到优化效果差不多的最优解,可明显提高搜索效率;与TS算法相比,在运行时间差不多的情况下,SA-TS可以很大程度地改善指配解的质量,提高了搜索精度. 为了分析算法稳定性,分别对模拟退火(SA)、禁忌搜索(TS)、混合智能优化(SA-TS)三种智能优化指配算法重复进行100次仿真,各算法仿真参数同3.1节,稳定性的对比结果如图7所示. 由图7(a)可知,在100次运行结果中,SA算法得到的指配解的代价值相对分散,多集中于代价值居中的区域,68%位于298~402,23%位于220~298,9%位于402~480.由图7(b)可知,TS算法得到的指配解质量较差,84%的代价值位于1 420~2 866,12%位于2 866~5 424,4%位于5 424~ 7 140.由图7(c)可知,在100次运行结果中,SA-TS混合算法的多数指配解集中于代价最低的优质解附近,84%是代价值位于40~512的优质解,14%的代价值位于512~1 456之间,只有2%的代价值大于1 792.由此可以看出,SA-TS混合算法的稳定性较好,优于SA、TS算法. (a) SA算法100次运行结果最优解代价值分布图 (b) TS算法100次运行结果最优解代价值分布图 (c) SA-TS算法100次运行结果最优解代价值分布图图7 不同方法最优解代价值分布图 针对模拟退火算法全局优化能力强,但优化过程较长、搜索效率较差的特点,考虑禁忌搜索算法局部优化能力强,搜索速度快,且拥有记忆功能的优点,提出了一种将二者相结合的混合智能优化频率指配算法,主体结构采用模拟退火算法,增加禁忌搜索算法的记忆功能,避免模拟退火算法搜索过程中由于执行概率接受环节而遗失当前最优解,通过增加存储环节,在搜索过程中保留中间最优解,并即时更新.仿真表明,混合算法可快速得到高质量的解,搜索效率和精度优于单用模拟退火或禁忌搜索算法,为解决大规模复杂网系的频率指配问题进行了有益的探索. [1] DUNKIN N, ALLEN S. Frequency Assignment Problems: Representations and Solutions[R]. London: Royal Holloway, University of London, 1997. [2] SMITH D H, ALLEN S M, HRULEY S, et al. Frequency Assignment: Methods and Algorithms[R/OL]. 1999[2012-10-27]. ftp://ftp.rta.nato.int/pubfulltext/RTO/MP/RTO-MP-013/$MP-013-$K.pdf [3] GLOVER F. Tabu search: part I[J]. ORSA Journal on Computing, 1989, 1(3): 190-206. [4] GLOVER F. Tabu search: part II[J]. ORSA Journal on Computing, 1990, 2(1): 4-32. [5] KIRKPATRICK S, GELATT Jr C D, VECCHI M P. Optimazation by simulated annealing[J]. Science, 1983, 220(4598): 671-680. [6]METROPOLIS N, ROSENBLUTH A, ROSENBLUTH M, et al. Equation of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 2: 1087-1092. [7] HOLLAND J H. Adaptation in Natural and Artificifal System[M]. Cambridge:University of Michigan Press, 1975. [8] RUDOLPH G. Convergence analysis of canonical genetic algorithms[J]. IEEE Transactions on Neural Networks, 1994, 5(1): 96-101. [9] DORIGO M. Optimization, Learning and Natural Algorithms[D]. Milano: Politecnico di Milano, 1992. [10] KENNEDY J, EBERHART R. A new optimizer using particle swarm theory[C]// 6th International Symposium on Micromachine and Human Science. Nagoya, October 4-6, 1995: 39-43. [11] CASTELINO D J, HURLEY S, STEPHENS N M. A tabu search algorithm for frequency assignment[J]. Annals of Operations Research, 1996, 63(2): 301-319. [12]MANUEL D, DIETMAR K, BERNHARD R. Channel assignment for cellular radio using simulated annealing[J]. IEEE Transactions on Vehicular Technology, 1993, 42(1): 14-21. [13] GHOSH S C, SINHA B P, DAS N. Channel assignment using genetic algorithm based on geometric symmetry[J]. IEEE Transactions on Vehicular Technology, 2003, 52(4): 860-875. [14] MANIEZZO V, CARBONARO A. An ANTS Heuristic for the frequency assignment problem[J]. Future Generation Computer System, 2000, 16(8): 927-935. [15] 王 景, 王振家, 范晓光. 频率分配算法及性能的仿真评估[C]//中国电子学会电子系统工程分会第五届军事信息软件与仿真学术研讨会论文集, 2006: 408-411. [16] 汪定伟, 王俊伟, 王洪峰, 等. 智能优化方法[M]. 北京: 高等教育出版社, 2007: 136-142.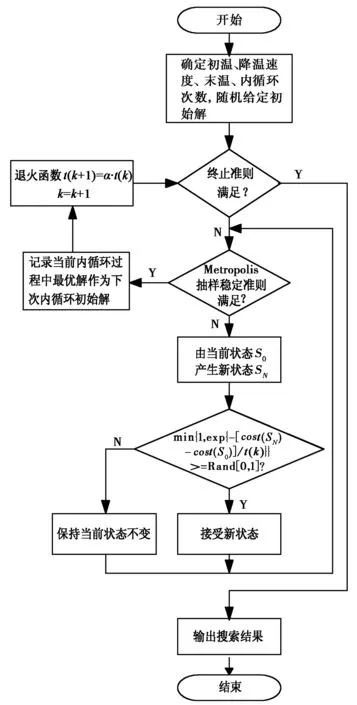
2 参数设置分析
3 算法对比分析
3.1 搜索效率和精度分析

3.2 稳定性分析

4 结 论

