天波雷达电离层信道建模

薛永华 柴 勇 刘宁波 关 键

(海军航空工程学院电子信息工程系，山东 烟台 264001)

引 言

天波超视距雷达利用电离层对高频信号的折射实现对远程目标的超视距探测.电离层是随机的、色散的、各向异性和双折射的复杂介质，其复杂性会严重影响天波雷达的目标探测.因此，建立天波雷达电离层信道模型，描述电离层对回波信号的影响，对天波雷达的设计和运作意义重大.

目前，国内外学者对电离层信道建模已经进行了大量研究，其中，大多数从短波天波通信的角度出发建立单向的传播模型，如Watterson模型[1]，电离层参数模型(IPM模型)[2]等.以上模型均为经验型模型，通过实测数据统计分析，加以数学抽象得到，结构简单，但是不能与具体信道条件准确对应.为了更精确地描述信道，人们从电离层电波传播的物理机制出发建立信道模型.电离层电波传播的物理机制较为复杂，按照作用机理和研究方法分为两大类：

一类是无随机变化的背景电离层对电波传播的影响，利用确定性方法研究，如全波法、射线追踪法等，其中射线追踪法应用较广.自20世纪50年代由Haselgrove等人奠定了完善的理论基础后，数值射线追踪方法得到了众多国内外学者的关注，数十年来，不断发展并得到了越来越广泛的应用[3-5].20世纪70年代，Jones等[3]开发了一组射线追踪程序，至今仍然被广泛采用或借鉴.为了改善精度和使程序更加实用，人们从多个方面对Jones等人的程序进行了改进，例如文献[4]用国际参考电离层(International Reference Ionosphere，IRI)模型产生电离层剖面，用国际地磁参考场(International Geomagnetic Reference，IGRF)模型替换了原有地磁场模型，还根据中国科学家的一些观测结果[6]，对国际参考电离层IRI-2007进行了修正；文献[5]在Jones等人的程序基础上，加入电离层电子浓度根据纬度、经度和高度三维离散化后的射线追踪计算，并基于MATLAB开发了直观的可视化界面.由于碰撞效应仅造成能量的吸收，对信号的传播路径影响不大，上述文献仅关心射线路径，故在计算中均忽略了碰撞效应.对于雷达信道而言，信道的衰减会影响雷达作用距离的预测，不同频率的信道衰减不同也会影响雷达发射频率的选择，因此，雷达的情形需考虑碰撞效应.

另一类是电子密度不规则体引起的随机电波传播，主要针对电波的电离层闪烁现象，利用随机和统计方法研究[7].研究表明，以Rytov解为核心的弱闪烁理论是比较满意的；对于强闪烁的情形，多相位屏方法(Multi-phase Method)和相位屏衍射方法(Phase Screen/Diffraction Method)更为适合.对天波雷达电离层信道的建模而言，既要考虑背景电离层对电波传播的影响，又要考虑电子密度不规则体引起的随机电波传播特性.然而，目前基于物理信道的模型[8-9]多数以单向传播为背景，仅关注其相关函数、散射函数等随机特性.文献[10]提出了一种基于相位屏衍射方法和数值射线追踪的高精度电离层信道模型，可适用于雷达情形.该模型考虑物理因素较为全面，适用性较好，但其采用的相关函数忽略了多普勒和角度-时延之间的相关性，该相关性，尤其是多普勒与时间的相关性对于在时频域的信号处理较为重要.另外，文中关于雷达情形下电离层信道建模的难点之一——收发射线路径的匹配也未给出详细的说明.

为解决上述问题，并进一步改善模型的通用性，首先，将IRI模型和IGRF模型的最新版本集成到Jones等开发的射线追踪代码中，在考虑碰撞效应的前提下，计算得到电离层中射线传播路径等参数；然后，针对雷达的情形，提出了一种新的收发射线路径匹配方法；最后，直接采用Nickisch给出的相关函数来描述信道的随机特性，该函数包涵了多普勒、角度和时延三者之间的相互耦合关系，利用该相关函数得到强闪烁下的随机信道冲击响应函数，对该函数进行修正，使得模型也适用于弱闪烁情形.对匹配的收发射线对应冲击响应函数进行二维卷积，并计入信道损耗，得到天波雷达双程信道模型.

1 基于IRI和IGRF的数字射线追踪

对于高频波段，电离层介质的特性在一个波长的范围内变化是很小的，高频传播一般与几何光学近似，可以利用射线追踪技术来研究电磁波的传播.天波雷达探测的情形，对射线追踪的精度要求较高，需全面地考虑电离层电子浓度、地磁场和碰撞效应等因素对电波传播的影响，进行三维数字射线追踪.

1.1 射线追踪原理

以地心为原点的极坐标系下，Haselgrove方程组如下：

(1)

(2)

(3)

(4)

(5)

(6)

式中：H表示哈密顿算符；kr，kθ和kφ分别为波矢量在r，θ，φ方向的分量.哈密顿算符H在射线传播中为常量，一般取

(7)

式中：c为光速；ω为发射电波角频率；n为相折射指数，考虑地磁场和碰撞效应时

n2= 1-2X[1-iZ-X/2(1-iZ)(1-iZ-X)-

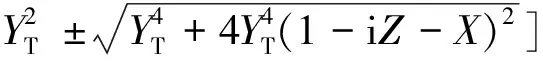
(8)

式中：

(9)

(10)

(11)

YT=Ysinψ；

(12)

YL=Ycosψ；

(13)

f2N=80.6·Ne；

(14)

式中：fN为介质频率；Ne为电子浓度 m3；fH为磁旋频率；υ为电子碰撞频率；f为发射电波频率；ψ为电波传播法向方向和地磁场的夹角.

射线追踪计算中，需计算射线路径上的X，Y，Z值.X是电子密度Ne的函数，Y是地磁场强度的函数，Z与电离层中带电粒子和中性粒子的碰撞效应有关.射线追踪计算以Jones等开发的射线追踪代码为基础，虽然Jones等人的代码中已经提供了一组电子浓度、磁场强度和碰撞效应的模块，但其所用模型已较为理想，不能满足需要.为改善模型通用性和计算精度，将IRI-2012和IGRF模型集成到射线追踪计算中.

1.2 IRI-2012模型的使用

目前，IRI模型的最新版本为IRI-2012.鉴于IRI-2012模型的复杂性，并未将其代码直接集成到射线追踪代码中.在射线追踪计算之前，首先，将射线路径可能经过的区域沿经度、纬度、高度离散化，这里，经纬度间隔取2°，高度间隔取1 km；然后，根据中国电离层工作者的建议[6]，对IRI-2012模型的输入参数进行设定，例如，在中国所有的季节均要考虑F1层的存在，E层的最大电子浓度高度hmE=115 km等；最后，利用IRI-2012模型来产生给定时间下，每个空间点上的电子浓度，保存为数据文件，以备射线追踪计算使用.在射线追踪计算时，将数据文件读入，计算中，当射线路径不在上述离散空间点时，其电子浓度通过对临近点的电子浓度进行插值运算得到.从运算量的角度考虑，应采用线性插值，但为保证一定的计算精度，而又不过多增加运算量，这里采用二次多项式插值方法.

图1为北纬25°上的一个电子浓度剖面，时间取2011年9月21日.图1(a)为北京时间12∶00，对应我国大部分区域(约在东经70°和140°之间)的中午时分，电子浓度较大；图1(b)为北京时间24∶00，对应我国大部分区域的午夜时分，电子浓度较小.

(a) 北京时间12∶00 (b) 北京时间24∶00图1 2011年09月21日电子浓度剖面

1.3 IGRF模型的集成

IGRF模型是一种计算公元1900年至今的地球表面和上空大尺度地磁场分量的数值模型，最新版本为第11代.将其集成到射线追踪程序中，只需对Jones等人的程序中的子过程HARMONY稍加修改即可.子过程HARMONY中高斯系数为7阶，将其调整为13阶，再将IGRF的高斯系数导入程序中即可，IGRF的高斯系数每5年一组，中间年份采用相邻年份加权求和得到.

1.4 射线追踪结果

电离层中带电粒子和中性粒子的碰撞，会造成电离层对高频雷达电波的吸收衰减[12].对碰撞效应的考虑，这里直接采用Jones等人的程序中提供的碰撞模型.图2为图1(b)所示的电子浓度条件下的一个射线追踪结果.计算中，仅考虑一跳传播的情形，发射频率取12 MHz，发射方位角与正北夹角为90°，俯仰角取值为5°～35°，间隔0.5°，每3°改变一次颜色.计算结果进行了坐标转换操作，从原先的地心为原点的球坐标系转换到以发射点为原点，正东为X′轴，竖直向上为Z′轴的右手直角坐标系.当俯仰角大于等于24.5°后，射线开始穿越电离层，对探测无贡献，显示中被剔除.

传播射线在X′-Z′平面的投影如图2(a)所示，显然在本算例中发射电波出现了双模传播.进一步的计算发现，途中射线的反射点与地球表面的距离均在230～310 km之间，故其传播模式为F2层.再根据射线追踪计算的结果，反射点的高低区分为高角模和低角模.故该算例中的传播模式为F2层的高角模和低角模.

受地磁场的影响，发射电磁波在电离层中的传播并不在发射方向所确定的平面(即X′-Z′平面)内，且不同发射仰角时，射线的传播路径与发射方向所在平面的偏移量不同.发射电磁波偏离传播平面的情况如图2(b)所示，射线的初始发射方向为X′轴正向，进入电离层后发生偏移，偏移方向与传播方向和发射仰角有关.射线的落地点均偏向一个方向，且随发射仰角的增大偏移距离增大，偏移距离最大值在0.4 km以内.该偏移距离与天波雷达所关注的目标尤其是大型舰船目标的几何尺寸相当，在目标探测及其坐标转换中需考虑这一问题.

(a) X′-Y′平面投影 (b) X′-Y′平面投影图2 射线追踪结果

1.5 波束覆盖区域预测

天波超视距雷达工作在高频频段(3～30 MHz)，通过高频电波的电离层传播来检测数千米外的目标.典型的天波超视距雷达系统[13]往往采用多组收发阵列覆盖所关心的区域，每组收发阵列采用一个发射阵和一个接收阵列，覆盖某一方位扇区.根据发射阵的波束宽度将该扇区按方位划分成若干个发射照射子区，每个发射照射子区又被若干个接收波束填满.

根据电离层参数空间相关半径及雷达搜索速率的要求，在方位扇区±30°内发射天线方位波束宽度需选择8°～12°；根据雷达方位分辨率要求，接收天线单个方位波束宽度为0.5°～2°；对于1000～2500 km的探测范围，仰角可取5°～35°[14].

令发射方位角方向波束宽度为10°，波束指向与正北夹角为90°，俯仰方向为5°～35°，方位角间隔0.5°，俯仰间隔0.1°，采用射线追踪的方法，在图1(b)相同情形的电子浓度条件下，计算电波传播路径，将其投影到地球表面，如图3所示，图中绿色多边形为射线地/海面脚印点的边界，绿色区域即为该发射波束照射区.

试验研究表明，中纬度电离层高频信道有较好的互异性.根据信道的互异性，将接收阵列作为射线追踪的发射点，取接收波束宽度为0.5°，波束指向与正北夹角为90°，俯仰方向为5°～35°，方位角间隔0.5°，俯仰间隔0.1°，在图1(b)相同情形的电子浓度条件下，采用射线追踪的方法，计算射线路径，得到图3中发射波束覆盖区域中该接收波束覆盖区域，如图中红色多边形区域所示.由图可知，受地磁场以及收发阵列不在同一位置等因素的影响，收发射线路径并不平行，有一定角度的视差.

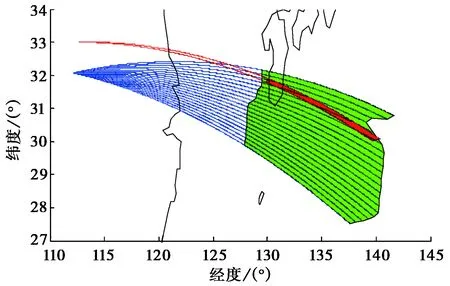
图3 发射波束覆盖示意图

2 收发射线路径匹配

天波超视距雷达要完成目标的探测，需要接收阵接收到目标对发射电磁波的反射回波，并对其进行处理.因此，与通信的单向传播不同，雷达情形下的信道建模，需考虑电磁波收发两次的穿越电离层传播.从射线追踪的角度建模，需要考虑的就是发射路径和接收路径之间的匹配问题.

2.1 收发射线路径匹配原理

从射线追踪的物理含义来看，每条射线的传播路径也是电磁波能量流动的路径.以射线追踪为基础，在主射线附近取一个小的方位角和俯仰角的偏移，计算该小空间立体角内的射线管在接收点处的面积，根据射线管内能流不变的原理计算出射线接收点处的能量密度，进而得到发射能量的空间分布，是一种重要的能量分布的近似计算方法[15].若主射线附近的方位角和俯仰角偏移量选取适中，可以得到较为满意的结果.根据这一思想，假设每条射线代表了其附近小空间立体角内的能量，将接收波束沿方位角和俯仰角进行二维离散化，每个离散点上进行射线追踪计算，射线路径在发射波束覆盖区的脚印点按顺序连线后形成一系列栅格，发射射线落在该栅格里，即认为该发射射线与栅格对应的接收射线匹配.

根据文献[15]，当方位角和俯仰角的偏移量减小到0.1°的量级时，能量分布计算结果与理论相近.另外，与电离层的高度不均匀相比，其水平不均匀较弱，射线追踪对于方位角的变化相对不敏感，故方位角的偏移量可取大些.在收发射线路径匹配计算时，接收波束方位角的离散间隔取0.5°，俯仰角离散间隔取0.1°.

2.2 匹配结果及分析

天波超视距雷达的覆盖方位较大，为方便讨论，这里仅考虑一个发射照射子区中发射射线路径与该发射子区中某一个接收波束宽度内接收射线路径的匹配问题，其他方位上可类似处理.

图4给出了图3相同情形下的收发射线匹配的部分匹配结果.图中红色点为接收射线的脚印点，蓝色线条为接收射线脚印点之间的连线，这些连线将接收射波束的覆盖区域分割成多个栅格，绿色的点为发射射线的脚印点，该脚印点落在某个栅格则认为，该脚印点对应的发射射线与栅格的其中一个顶点对应的接收射线匹配.由于电离层的多层性，计算中收发射线路径均出现了多模传播的现象，收发射线均有F层低角模和高角模两种传播模式.为清晰显示，图4中将接收射线的高角模和低角模的部分匹配结果分别绘出.

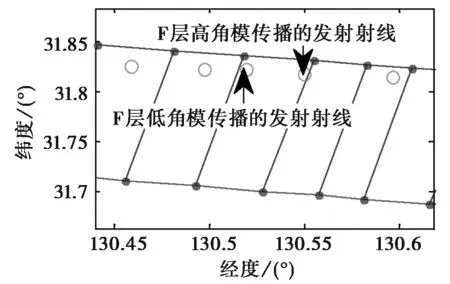
(a) 接收射线F层低角模传播

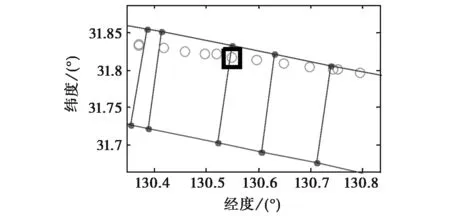
(b) 接收射线F层高角模传播图4 收发射线路径匹配结果的局部

从中可以看出，收发射线的匹配并非一一对应关系，对于某一条接收射线可能存在多条发射射线与之匹配，且有可能多条发射射线并非同一传播模式.如图4(a)所示，一条接收射线与两条发射射线匹配，且两条射线分属两种传播模式.对于某一发射射线而言，也并非仅有一条接收射线与之匹配，图4(a)栅格中的F层低角模传播的发射射线，即图4(b)中黑色矩形框中的脚印点对应的发射射线，又与某一高角模传播的接收射线相匹配.由此可见，电离层的多层性进一步增加了电离层信道的复杂性，也增加了建模的难度和复杂度.

3 电离层信道模型的建立

电离层中电子密度随机、快速的不均匀变化，会导致穿越电离层的无线电信号振幅、相位和偏振方向的快速随机起伏，即电离层闪烁.天波雷达电离层信道的仿真中，应考虑发射电磁波信号的电离层闪烁效应.观测表明，我国北方大部分区域处在中纬度地区，电离层闪烁较弱，但我国长江(上海、武汉、重庆)以南的低纬度地区，特别是台湾、福建、广东、广西、海南及南海地区，均处在磁赤道异常区的驼峰附近区域，其电离层闪烁出现率和严重程度较磁赤道和极区都显著，在全球范围内是电离层闪烁衰落出现最频繁、影响最严重的地区之一[16].故在电离层建模时，需同时考虑强闪烁和弱闪烁的情形.

弱闪烁和强闪烁理论方面，人们已经进行了大量的研究，其中，针对弱闪烁情形的相位屏理论、强闪烁情形的多相位屏理论、相位屏/衍射方法等已经被用于HF信号的建模.文献[10]中，相位屏衍射方法被用于天波雷达信道建模，并采用Rician方法得到的信道函数修改后，亦可适用于弱闪烁的情形，扩展了模型的适用性.但其在得到信道函数过程中采用了Dana等[11]给出的相关函数，该相关函数忽略了多普勒和角度-时延之间的相关性，该相关性，尤其是多普勒与时间的相关性对于在时频域的信号处理较为重要.为考虑这一影响，采用文献[9]给出的双频、双点、双时相关函数

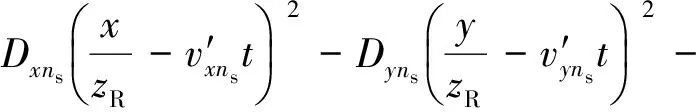
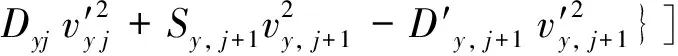
(15)

式中：ωd表示频率间隔； (x，y)表示空间间隔；t表示时间间隔；zR表示射线接收点的Z轴坐标；ns表示薄屏的个数，各中间量表达式如下：

(16)

(17)

D′xi=Dx，i-1+Sxi；

(18)

(19)

(20)

(21)

(22)

(23)

式中：c表示光速；k表示发射电磁波波数；zi表示第i个薄屏的位置；vxi，vyi表示第i个薄屏上介质的运动速度； Δi表示第i个薄屏和第i+1个薄屏之间的距离；kpi表示第i个屏上的介质波数；Ao，A2x，A2y为电离层介质中不规则体切向自相关函数二次近似系数，计算方法见文献[9]附录.

式(15)所表示的相关函数是通过相位屏/衍射方法直接得到的，包涵了信道空、时、频相关特性.这里以某一条射线路径为例，阐述其计算过程.

首先，将射线轨迹点坐标进行转换，从以地心为原点的球坐标系转换到以发射点为原点，发射点指向接收点的方向为z轴，地心指向收发点连线的中点方向为x的右手直角坐标系中，沿y轴方向，按照射线路径传播方向角度的等间隔变化在传播空间放置若干个薄相位屏.

其次，计算式(15)中相关参数.在式(15)中，令空间分量(x，y)为0，对t和ωd进行二维傅里叶变换即可得到多普勒-时延谱.根据文献[9]相位屏个数大于12后，其计算结果可逼近抛物方程的精确解.图5为某一条射线上取13个相位屏计算得到的多普勒-时延谱.从图5来看，电离层信道的时延和多普勒扩展是有一定相关性的.

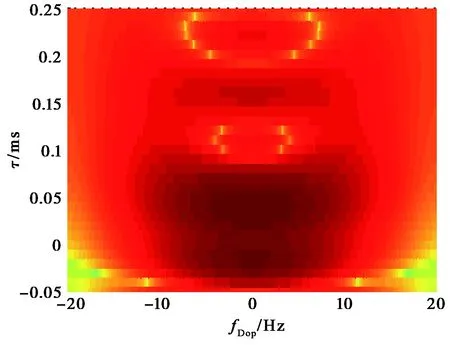
图5 多普勒-时延谱

互相关函数进行傅里叶变换可得到相应的广义功率谱函数

GPSD(ωDop，τ，Kx，Ky)=FFT{Γ(ωd，x，y，t；zR)}，

(24)

式中：ωDop表示多普勒频率；τ表示时延；Kx与Ky分别表示沿x轴和y轴方向的空间波数分量.

相应地，冲击相应函数：

exp{-i(Kxx+Kyy-

ωDopt)}dxdydωDop，

(25)

式中r为单位方差的复高斯随机数.

为使模型可用于弱闪烁的情形，这里同样采用Racian方法，得到弱闪烁时的冲击响应函数：

hweak(x，y，ωDop，τ)=υδ(ωDop)δ(τ)+

σh(x，y，ωDop，τ)，

(26)

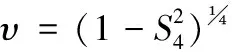
对于雷达的情形，双程信道函数通过往返路径匹配的单程信道的冲击响应函数在时延和多普勒维进行二维卷积运算，并计入相应的电离层吸收衰减系数即可得到，用公式表示如下

hT(x，y，t′-t，τ′-τ)dt′dτ′，

(27)

式中：LT，LR分别为收发路径的电离层信道损耗，具体计算方法见文献[12]；t表示时间间隔，与广义功率谱函数的多普勒维相对应；τ表示时延.

4 结 论

从电离层中电波传播的物理机制出发，以三维射线追踪和相位屏/衍射方法为基础，建立了一种天波超视距雷达电离层信道模型.模型中的射线追踪计算集成了IRI-2012模型和IGRF模型，提出了一种新的收发射线匹配方法.通过相位屏/衍射方法直接得到的信道双频、双点、双时相关函数，进而得到强闪烁下的随机信道冲击响应函数，考虑了信道的空时频相关特性，对该冲击响应函数进行修正，使得模型也适用于弱闪烁的情形.对匹配的收发射线对应冲击响应函数进行二维卷积，并计入信道损耗，得到天波雷达双程信道模型.

该模型较为全面地考虑了电离层中电波传播的物理机制，可以较为精确地描述不同电子浓度、地磁场强度、碰撞特性和闪烁强度下的天波超视距雷达电离层信道，能够与信道的具体物理条件相对应，精度高，通用性较好，可以用于天波雷达信号仿真和后续信号处理的研究，同时，也可方便地推广到单向的通信信道建模中.

[1] WATTERSON C C, JUROSHEK J R, BENSEMA W D. Experimental confirmation of an HF channel model[J]. IEEE Transactions on Communication Technology, 1970, 18(6): 792-803.

[2]VOGLER L E, HOFFMEYER J A. A model for wideband HF propagation channels[J]. Radio Science, 1993, 28(6): 1131-1142.

[3] YAN Zhaowen, WANG Gang, TIAN Guoliang, et al. The HF channel EM parameters estimation under a complex environment using the modified IRI and IGRF model[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(5): 1778-1783.

[4] AZZARONE A, BIANCHI C, PEZZOPANE M, et al. IONORT: a Windows software tool to calculate the HF ray tracing in the ionosphere[J]. Computers &Geosciences, 2012, 42(2012): 57-63.

[5] JONES R M, STEPHENSON J J. A Versatile Three-dimensional Ray Tracing Computer Program for Radio Waves in The Ionosphere[R]. Colorado: National Geophysical Data Center, 1975.

[6] 焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007.

[7] YEH K C, LIU C H. Radio wave scintillations in the ionosphere[C]//Proceeding of the IEEE, 1982, 70(4): 324-360.

[8] GHERM V E, ZERNOV N N, STRANGEWAYS H J. HF propagation in a wideband ionospheric fluctuating reflection channel: Physically based software simulator of the channel[J]. Radio Science, 2005, 40(RS1001): 1-15.

[9] NICKISCH L J. Non-uniform motion and extended media effects on the mutual coherence function: An analytic solution for spaced frequency, position, and time[J]. Radio Science, 1992, 27(1): 9-22.

[10] NICKISCH L J, JOHN G S, FRIDMAN S V, et al. HiCIRF: A high-fidelity HF channel simulation[J]. Radio Science, 2012, 47(RS0L11): 1-10.

[11] DANA R A, WITTWER L A. A general channel model for RF propagation through structured ionization[J]. Radio Science, 1991, 26(4): 1059-1068.

[12] 何 昉, 赵正予. 电离层对高频电波吸收衰减的影响研究[J]. 电波科学学报, 2009, 24(4): 720-723.

HE Fang, ZHAO Zhengyu. Ionospheric loss of high frequency radio wave propagated in the ionospheric regions[J]. Chinese Journal of Radio Science, 2009, 24(4): 720-723. (in Chinese)

[13] DANDEKAR B S, BUCHAU J. The AN/FPS-118 OTH Radar: Chapter 5, OTH Handbook[R]. Bedford: Hanscom Air Force Base, 1996.

[14] 周文瑜, 焦培南. 超视距雷达技术[M]. 北京: 电子工业出版社, 2008.

[15] NICKISCH L J. Focusing in the stationary phase approximation[J]. Radio Science, 1988, 23(2): 171-182.

[16] 李国主. 中国中低纬电离层闪烁监测、分析与应用研究[D]. 武汉: 中国科学院地质与地球物理研究所, 2007.

LI Guozhu. Studies on Monitoring Analysis and Application of Chinese Mid-and Low Latitude Ionospheric Scintillation[D]. Wuhan: Institute of Geology and Geophysics, Chinese Academy of Sciences, 2007. (in Chinese)