基于空间映射法的微带双频滤波器优化设计

赵惠玲 王 斐 张国玺 万国宾

(西北工业大学 电子信息学院，陕西 西安 710129)

引 言

近年来，随着无线移动通信技术的持续发展，人们对工作在两个甚至多个频段的射频通信系统的需求越来越迫切. 双频滤波器作为这些系统重要的前端器件，引起广泛的关注[1]. 由于双频滤波器需要设计两个工作频段，频率计算范围较宽，且优化参数较多，模型结构较复杂，若直接采用传统全波电磁仿真工具设计，虽然可以保证较好的设计精度，但耗费的时间成本和硬件资源严重制约着滤波器的快速实现，这对迫切希望微波器件小型化、高性能的通信需求显然是不利的. 因此，寻求一种既有电路模型的优化效率，同时又满足工程可接受精度的设计方法便显得十分紧迫.

空间映射方法正好迎合了这种需求. 它是John W. Bandler等在1994年首次提出的，融合电路仿真快速性与电磁仿真准确性的一种新的优化、建模思想[2]. 早期的空间映射算法需要预先假定粗糙模型和精确模型的参数空间是线性关系，并需要大量先验基点的仿真结果来建立该映射，其优化效率和适用范围均较低. 因此其后出现较多改进算法，如渐进空间映射[3]及其变形，隐式空间映射法[4](Implicit Space Mapping, ISM)等. 其中ISM算法利用微带电路的介电常数和厚度值等自由量作为预定参数来构建映射关系，从而避免了之前算法中的矩阵求解过程，提高了算法的自由度和灵活性. 算法的不断改进为算法的应用拓展了空间. 近年来，空间映射法开始用于射频器件的优化和设计. 例如，利用渐进空间映射法设计单频段低温共烧陶瓷滤波器[5]、平面贴片天线和双环天线[6]；将空间映射算法与遗传算法结合，优化设计车载天线或共形天线等[7-8]. 研究表明，在电磁领域的应用中，该方法可以提高一些单频段滤波器的设计效率，此外，其在微带天线的驻波特性优化中也有不错表现，但针对双频滤波器的优化设计，除文献[9]外，未见有报道. 鉴于双频滤波器的相对复杂性和重要性，能够建立一种可行的优化设计方法，无疑将具有很好的应用价值和推广应用前景.

空间映射算法中，保证算法收敛的关键步骤是参数提取和参数迭代优化. 针对微带双频滤波器的隐式空间映射法优化设计中的弱收敛问题，采用一种具有约束的参数提取方法，有效提高算法的收敛性，最后通过算例验证算法的可行性.

1 理论分析

1.1 隐式空间映射算法

空间映射算法通过建立同一物理系统的粗糙模型设计参数与精确模型设计参数之间的数学联系(通常是一种映射关系)，来获得一组合适的粗糙替代模型. 该替代模型的优化效率一般高于精确模型，且至少拥有粗糙模型的准确度. 通过不断更新替代模型，并将其优化迭代结果导入精确模型予以仿真验证，直至满足指标要求则停止优化.

一般一个优化问题可以表示为

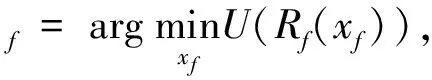
(1)

式中：Rf∈m×1表示精确模型下m个响应点组成的响应矢量；xf∈n×1代表由n个设计参数组成的参数矢量，在电磁仿真中可以是器件的长、宽和厚度等；U是目标函数表示精确模型参数空间的一组理想最优值，优化的过程就是不断地接近该理想值.

考虑到精确模型电磁仿真通常比较耗时耗资源，一般认为直接优化求解式(1)是不现实的. 因此，常见的方法是优化其粗糙模型，它是精确模型某种程度的近似，如采用微波等效电路或经验公式来替代全波电磁仿真. 粗糙模型计算效率很高，但精确度较差，式(1)的优化问题在粗糙模型中可以表示为

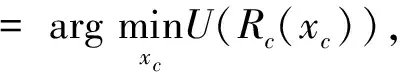
(2)

式中，参数Rc，xc，xc*等定义与式(1)精确模型相似.

3.将起酥面擀为 0.1～0.2 cm厚的一大张面片，用扣碗扣为饺子皮。包馅制成饺子。饺子皮外抹上蛋黄，放入烤箱，用230～250℃箱温将饺子烤熟。

空间映射算法就是寻求精确模型参数xf和粗糙模型参数xc之间的映射关系. 映射关系的建立是一个反复迭代的过程：通过优化替代模型的设计参数，使响应达到指标要求，将所得参数值导入精确模型中进行验证计算. 如此反复迭代，直到精确模型的响应结果达到指标要求，算法终止.

隐式空间映射利用单元电路的介电常数和厚度值等自由量作为辅助参数来构建映射关系为

Q(xf，xc,p)=0 ,

(3)

使得

(4)

成立. 式中Rs为改变辅助参数的粗糙模型响应，已不同于式(2)中的粗糙模型响应，称为替代模型响应. 上标i表示在第i步迭代中的相应参数. 式中p为辅助参数，是替代模型响应最佳逼近相应精确模型响应时的值，即

(5)

辅助参数提取完成后，优化替代模型得到新的设计参数值

(6)

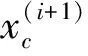
1.2 具有约束的隐式空间映射算法

在隐式空间映射迭代过程中，参数提取是映射关系建立的关键，但往往存在参数提取不唯一的问题，导致算法弱收敛或不收敛. 针对参数提取的文献己经很多[10-11]，如多点参数提取、统计参数提取、罚函数参数提取等. 考虑到双频滤波器需要优化两个工作频段，频率响应范围较宽，多点参数提取显然不是一个合适的选择. 因此，采用单点参数提取，为了确保提取的准确性，对其施加相应的约束条件，保证算法收敛. 单点隐式参数提取表示为

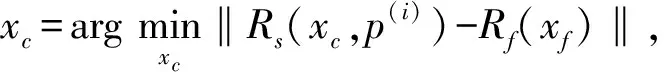
(7)

对辅助参数p施加的约束条件为

(8)

i=1时，在微带电路优化中，辅助参数为基板介电常数和厚度的固有标称值，随着迭代的执行，p(i)在约束范围内优化提取.

具有约束的参数提取方法能够对映射的非唯一性予以适当限制，较好保持了单点参数提取的便捷特点，使精确模型响应以较稳健的速度向要求指标逼近，改善算法的收敛效率.

2 算例仿真及实验分析

微带双模滤波器具有面积小、插损低等优点，在微波无源电路研究领域引起人们越来越多的关注[11]. 双模双频滤波器，是由于所激励的简并模分裂而产生双频特性. 为设计一工作在WLAN和WiMAX频段的双模双频带通滤波器，在环形谐振滤波器[12]结构基础上加入方形微扰元，以使不同的简并模式分裂，产生需要的双频响应，结构如图1所示. 待优化的设计参数为各单元枝节的长度和耦合间隙，即xf=[l1，l2，l3，l4，l5，s]，单位均为毫米. 采用的微带基板介电常数为10.2，损耗角正切0.002 3，厚度0.635 mm，微带线的宽度值W1=0.6 mm，W2=0.2 mm，滤波器的设计指标为：

中心频率： 3.45 GHz，5.7 GHz；

通带带宽： 100 MHz，200 MHz；

回波损耗： 15 dB .

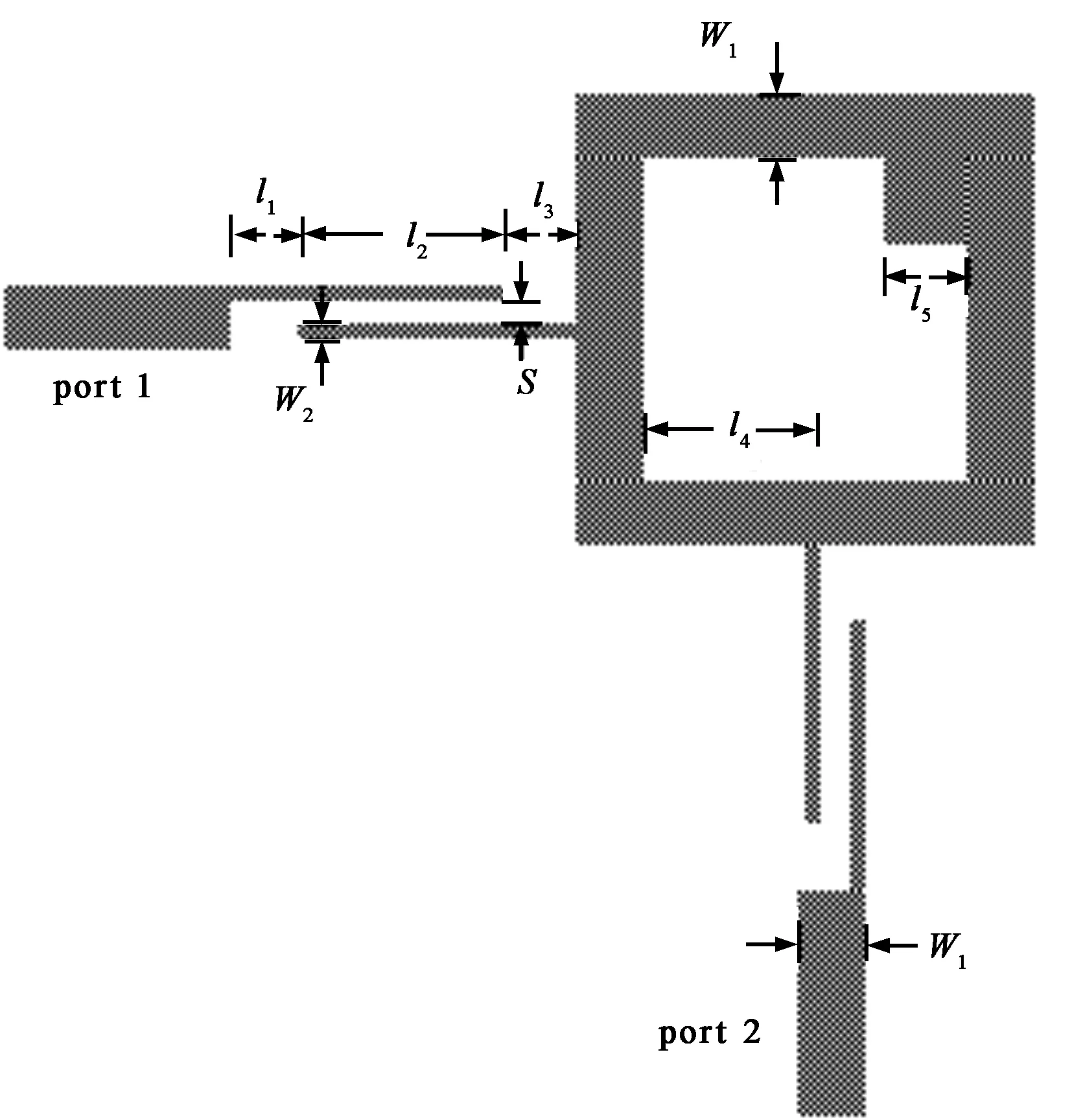
图1 双频滤波器结构图

双模双频带通滤波器的粗糙模型采用Agilent ADS建立的等效电路模型，如图2所示，其中W、L和S分别表示微带线宽度、长度和耦合间隙. 精细模型由基于矩量法的FEKO电磁仿真软件给出. 首先，优化粗糙模型，获得一组满足指标的初始设计值. 图3是该初始最优值分别在粗糙模型和精细模型下的响应结果，显然二者有较大差别，精确电磁模型的响应明显不满足指标.

其次，利用ADS的变量插件等工具，建立隐式空间映射算法. 选择七组滤波器单元枝节，将其介电常数和厚度值作为待提取的辅助参数，即p=[e1，h1，e2，h2，e3，h3，e4，h4，e5，h5，e6，h6，e7，h7]，其中，e1和h1为传输线1和传输线6的介电常数和介质厚度，e2和h2为耦合线1和耦合线2的介电常数和厚度，e3和h3为传输线2和传输线5的介电常数和厚度，e4和h4为传输线3、传输线4、传输线7和传输线11的介电常数和介质厚度，e5和h5为拐角线1、拐角线2和拐角线3的介电常数和厚度，e6和h6为传输线8 和传输线10的介电常数和厚度，e7和h7为传输线9的介电常数和介质厚度. 设定介电常数和厚度的初始值分别为10.2和0.635 mm，采用梯度优化提取辅助参数，使粗糙模型响应与当前的精确模型响应尽可能匹配，如图4所示. 需要说明的是，粗糙模型的辅助参数要随着映射的迭代更新而发生相应变化，如表1所示，而精确模型的介电常数和厚度值始终固定不变.

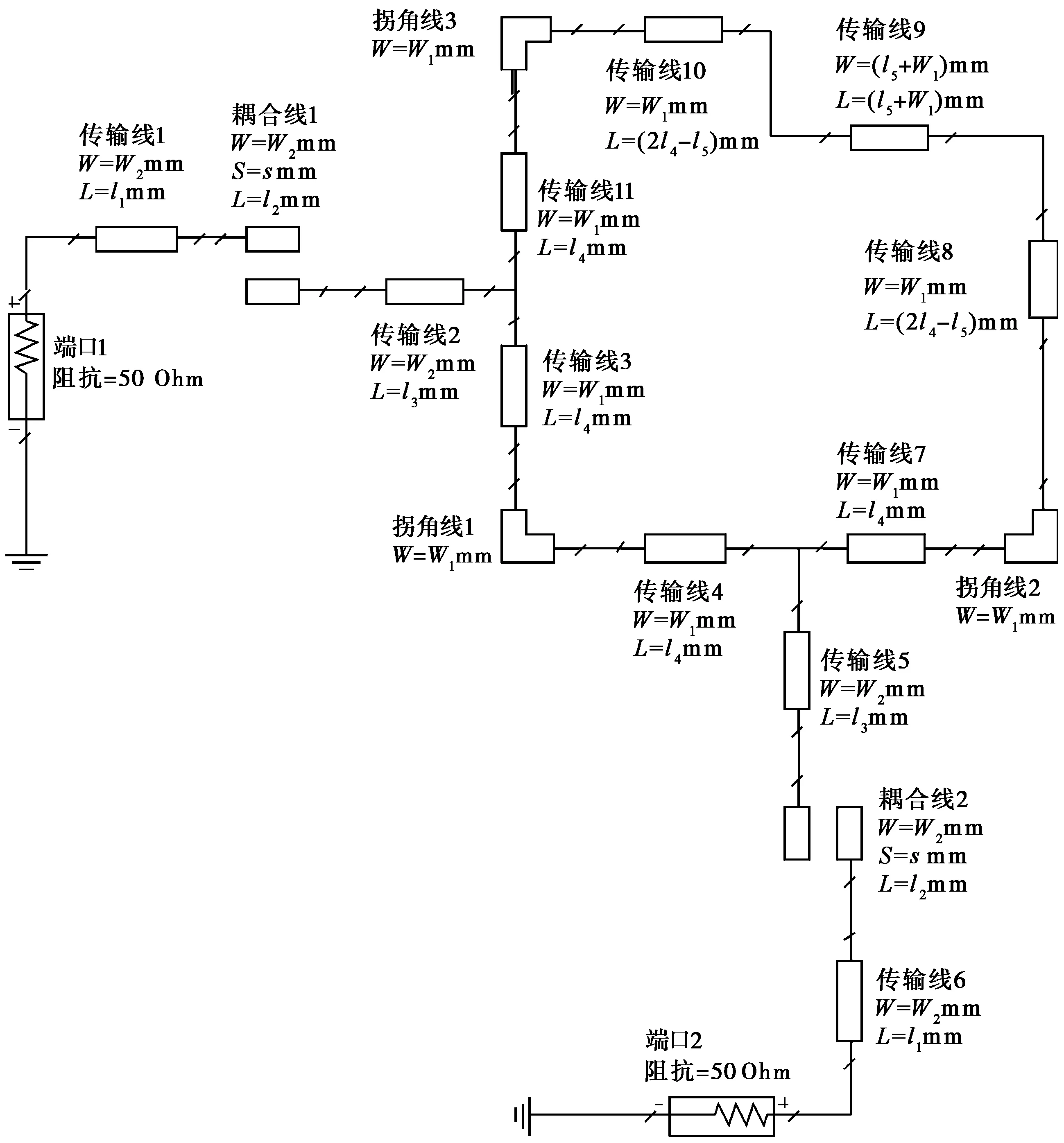
图2 双频滤波器电路模型

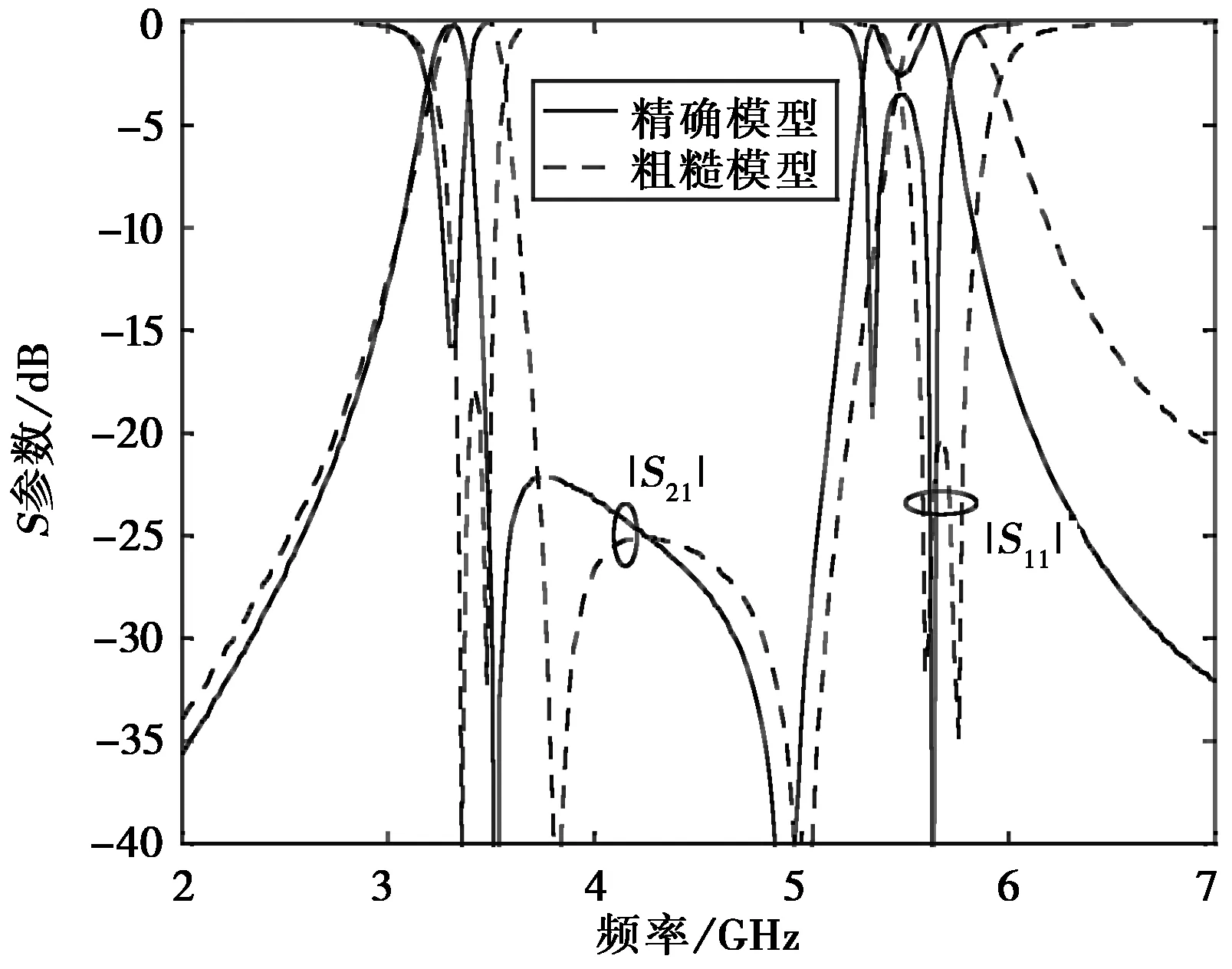
图3 双频滤波器初始最优值响应

最后，保持辅助参数不变，再次优化粗糙电路模型下滤波器的设计参数，以满足要求指标，并导入精确电磁模型予以验证，重复以上过程直至精确电磁模型的响应满足指标，则算法结束. 该算例经四次迭代优化，即获得满足指标的一组解. 全部优化过程耗时约3 h，计算机处理器为奔腾3.0 GHz. FEKO仿真一次约需18 min，网格剖分尺寸为一个波长15份，局部略细剖. 辅助参数和设计参数的迭代过程见表1和表2.

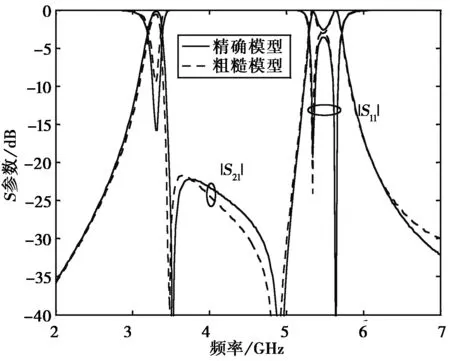
图4 初始设计值辅助参数提取后的响应

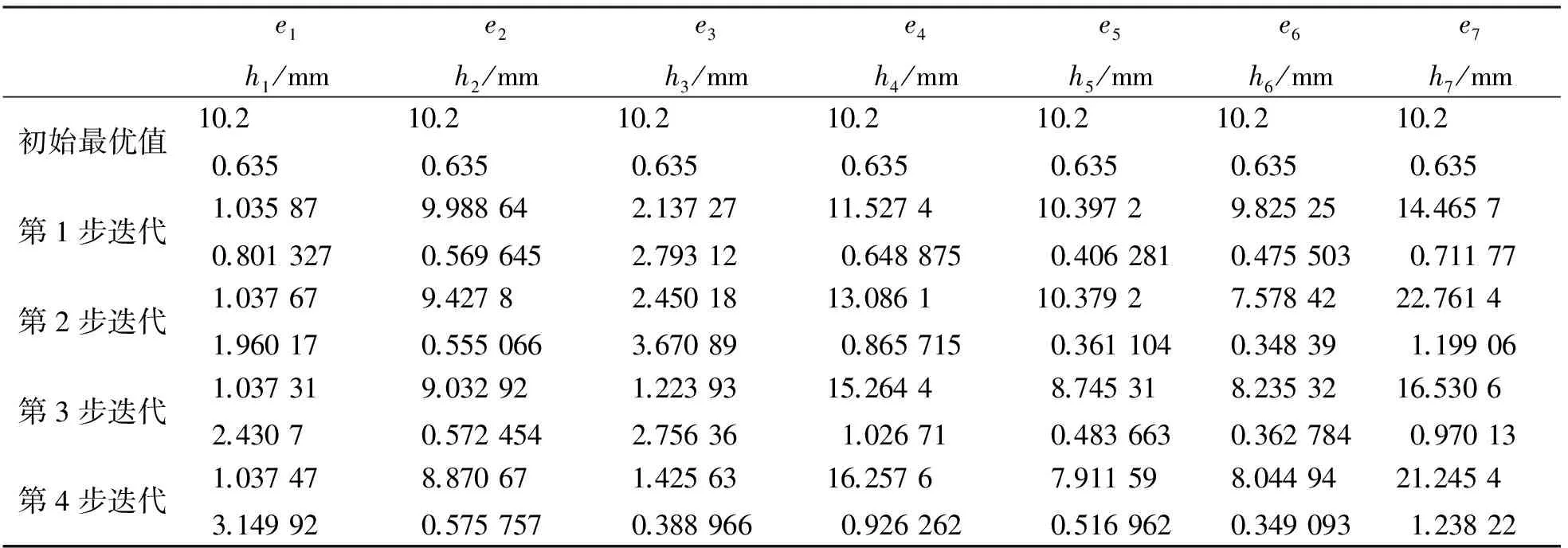
e1h1/mme2h2/mme3h3/mme4h4/mme5h5/mme6h6/mme7h7/mm初始最优值10．20．63510．20．63510．20．63510．20．63510．20．63510．20．63510．20．635第1步迭代1．035870．8013279．988640．5696452．137272．7931211．52740．64887510．39720．4062819．825250．47550314．46570．71177第2步迭代1．037671．960179．42780．5550662．450183．6708913．08610．86571510．37920．3611047．578420．3483922．76141．19906第3步迭代1．037312．43079．032920．5724541．223932．7563615．26441．026718．745310．4836638．235320．36278416．53060．97013第4步迭代1．037473．149928．870670．5757571．425630．38896616．25760．9262627．911590．5169628．044940．34909321．24541．23822

表2 滤波器设计参数迭代过程

根据表2优化结果，参考加工精度降低尺寸精度，仿真验证满足指标要求，再进行实物加工. 图5给出了滤波器的加工实物图，总尺寸小于22 mm ×22 mm. 比较实测曲线和仿真曲线，发现二者谐振频率有偏差. 经查阅文献，在Rogers公司网站找到了该基板的参数说明，文件指出，虽然材料的标称值为10.2，但由于制板工艺问题，使真实值偏大，建议实际设计值取10.9为宜[13]. 介电常数修正为10.9后，仿真结果与实测结果吻合较好，如图6所示. 实测曲线中，滤波器中心频率分别在3.37 GHz和5.56 GHz，中心插入损耗为1.16 dB和3.42 dB，带内回波损耗分别大于16.5 dB和6 dB，第二通带结果与指标有较大偏差，这主要由于加工误差和小A型(Small A Type,SMA)焊接头处理导致的第二通带性能变差.

图5 双频滤波器实物图

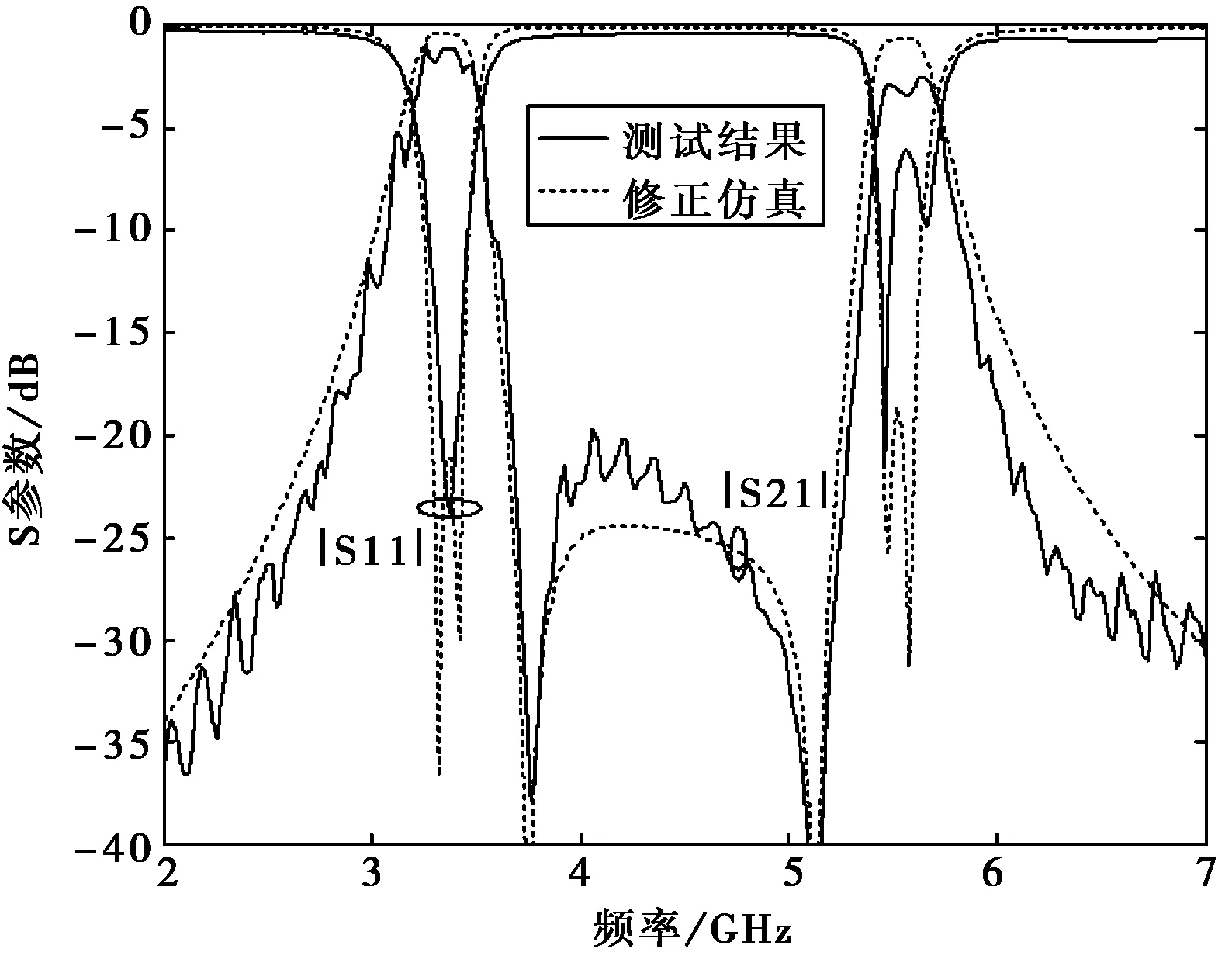
图6 双频滤波器测试和修正仿真结果比较

3 结 论

采用具有约束的隐式空间映射方法优化设计了工作在WLAN和WiMAX频段的微带双模双频滤波器. 在隐式空间映射算法的参数提取过程中，将文献[9]的参数提取方法改进为有约束的参数提取方法，通过对映射辅助参数予以适当限制，可以较好避免映射的非唯一性，使待优化器件响应以更稳健的速度向要求指标逼近，改善了隐式空间映射算法的收敛效率. 最后加工实物，进行测量，测试结果和仿真结果吻合较好. 验证了具有约束的隐式空间映射方法能够较快、准确地优化设计微带双频带通滤波器，有效节省器件的优化时间，提高设计效率.

具有约束的隐式空间映射方法能够方便应用于显式空间映射和隐式空间映射，方法通用性较好，可用于基于阶跃阻抗谐振器和基于半波长均匀阻抗谐振器等的微带双频滤波器优化设计.

[1] 张忠海,官伯然. 采用新型介质集成波导腔的小型双频滤波器[J] .电波科学学报, 2012, 27(2):321-325.

ZHANG Zhonghai, GUAN Boran. Novel compact dual-band bandpass filter adopting SIW cavity[J]. Chinese Journal of Radio Science, 2012, 27(2): 321-325. (in Chinese)

[2] BANDLER J W, BIEMACKI R M, CHEN Shaohua, et al. Space mapping technique for electromagnetic optimization[J]. IEEE Transactions on Microwave Theory and Techniques, 1994, 42(12): 2536-2544.

[3] BANDLER J W, BIEMACKI R M, CHEN Shaohua, et al. Electromagnetic optimization exploiting aggressive space mapping[J]. IEEE Transactions on Microwave Theory and Techniques, 1995, 43(12): 2874-2882.

[4] BANDLER J W, CHENG Q S, NIKOLOVA N K, et al. Implicit space mapping optimization exploiting preassigned parameters[J]. IEEE Transactions on Microwave Theory and Techniques, 2004, 52(1): 378-385.

[5] WU K L, ZHANG R, FANG D G. An explicit knowledge-embedded space mapping technique and its application to optimization of LTCC RF passive circuits[J]. IEEE Transactions on Components and Packaging Technologies, 2003, 26(2): 399-406.

[6] ZHU J, BANDLER J W, NIKOLOVA N K, et al. Antenna optimization through space mapping[J]. IEEE Transactions on Antennas and Propagation, 2007, 55(3): 651-658.

[7] 袁 军, 邱 扬, 刘其中, 等. 基于空间映射及遗传算法的车载天线优化配置[J]. 电波科学学报, 2006, 21(1): 28-34.

YUAN Jun, QIU Yang, LIU Qizhong, et al. Position optimal design of vehicular antenna via space mapping and genetic algorithm[J]. Chinese Journal of Radio Science, 2006, 21(1): 28-34. (in Chinese)

[8] 欧阳骏. 共形天线及阵列的分析和综合研究[D]. 成都: 电子科技大学, 2008.

OUYANG Jun. Analysis and Synthesis of Conformal Antenna and Array[D]. Chengdu: University of Electronics Science & Technology of China, 2008. (in Chinese)

[9] ZHANG Guoxi, ZHAO Huiling. Optimization of microstrip dual-band filter with implicit space mapping algorithm[C]// 2011 IEEE International Conference on Signal Processing, Communications and Computing. Xi'an: 2011.

[10] BANDLER J W, CHENG Q S, DAKROURY S A, et al. Space mapping: the state of the art[J].IEEE Transactions on Microwave Theory and Techniques. 2004, 52 (1): 337-361.

[11] 刘海文. 一种RBF 神经网络辅助设计的新型微带双模滤波器[J]. 电波科学学报, 2009, 24(2): 372-377.

LIU Haiwen. A novel microstrip dual-mode filter design based on RBF nneural network CAD[J]. Chinese Journal of Radio Science, 2009, 24(2): 372-377. (in Chinese)

[12] SUN S. A dual-band bandpass filter using a single dual-mode ring resonator[J]. IEEE Microwave and Wireless Components Letter, 2011, 21(6): 298-300.

[13] ROGERS CORPORATION, Ordering information: 高频产品选材指南[DB/OL]. 2011[2012-08-06], http://www.rogerscorp.com/acm/ordering.aspx.